

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...
Топ:
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Интересное:
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
| Номер шпангоута, i(i ¢ ) | Ординаты ватерлинии | Произведение: i(yi – yi ¢ ) | |
| носовые | кормовые | ||
| y 0 | |||
| y 1 | y 1¢ | (yi– yi ¢) | |
| y 2 | y 2¢ | 
| |
| y 3 | y 3¢ | 
| |
| . . . | . . . | . . . | . . . |
| n – 1 | yn- 1 | y (n -1)¢ | (n – 1) (yn –1 – y (n– 1)¢) |
| n | yn | yn¢ | 
|
| Сумма S¢ | 
| 
| |
| Поправка DS | 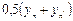
| 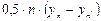
| |
| Исправленная сумма S | S yi | 
| |
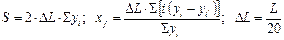
|
Расчет объемного водоизмещения. Общие выражения, определяющие зависимость величины погруженного объема от характеристик теоретического чертежа представлены формулами (1.4) (1.7) (1.14) и (1.15).
При известных значениях площади шпангоутов (известной строевой по шпангоутам – см. рис. 1.11) и исходя из выражения (1.4) по правилу трапеций нетрудно получить формулу для расчета объемного водоизмещения
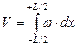 ≃ ≃ 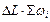 , ,
| (1.27) |
| где | 
| – | теоретическая шпация; |
| S wi | – | исправленная сумма площадей шпангоутов. |
Если при заданной посадке судна известны площади ватерлиний, то, с учетом (1.7), расчет объемного водоизмещения по правилу трапеций выполняется по формуле
 ≃ ≃  , ,
| (1.28) |
| где | 
| – | интервал между плоскостями ватерлиний; |

| – | исправленная сумма площадей ватерлиний; | |
| m | – | номер расчетной ватерлинии. |
Правило трапеций позволяет получить формулу для расчета объемного водоизмещения с использованием ординат точек пересечения шпангоутов и ватерлиний, т.е.  (где i – номер шпангоута, j – номер ватерлинии). В этом случае, исходя из зависимости (1.14), расчетную формулу можно получить в виде
(где i – номер шпангоута, j – номер ватерлинии). В этом случае, исходя из зависимости (1.14), расчетную формулу можно получить в виде
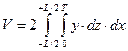 ≃
≃  ,
,
а при использовании выражения (1.15) формула получается в виде
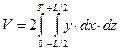 ≃
≃  ,
,
| где | D Т, D L | – | см. пояснения к формулам (1.27) (1.28); |
| SS yj | – | исправленная сумма исправленных сумм ординат, снятых (измеренных) по ватерлиниям; | |
| SS yi | – | исправленная сумма исправленных сумм ординат, снятых по шпангоутам. |
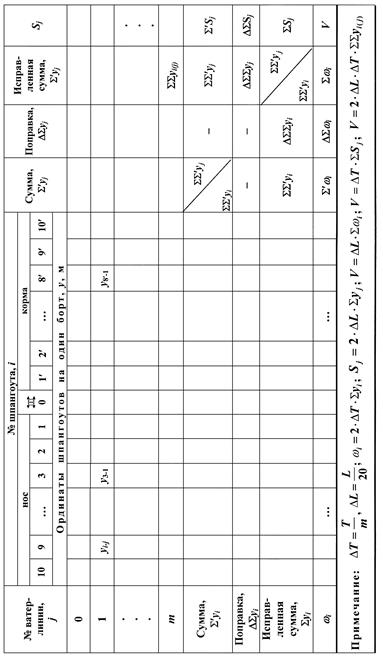
Порядок вычисления исправленной суммы исправленных сумм (SS y) или, иначе, двойной суммы ординат, показан в табл. 1.3. Сумма SS yi или SS yj в результате расчетов записывается в табл. 1.3 на пересечении строки с обозначением S yi и графы с обозначением S yj. При определении SS yi в качестве ряда чисел используются значения S yi, а при определении SS yj – значения S yj.
|
|
Табл. 1.3 является комплексной; она содержит схемы расчета объемного водоизмещения с использованием: ординат (уij), площадей шпангоутов (wi) и площадей ватерлиний (Si). Площади шпангоутов и ватерлиний также определяются по форме табл. 1.3.
Вначале в табл. 1.3 вносят значения ординат, которые замеряются по теоретическому чертежу. Независимо от его масштаба, ординаты следует указывать в натуральную величину (для «натуры») в метрах.
Значение двойной суммы  должно быть одинаковым при вычислении, как по вертикали, так и по горизонтали, поскольку в обоих случаях находится сумма всех ординат, занесенных в таблицу.
должно быть одинаковым при вычислении, как по вертикали, так и по горизонтали, поскольку в обоих случаях находится сумма всех ординат, занесенных в таблицу.
Расчет координат центра величины (центра тяжести подводного объема корпуса судна).
Вследствие симметрии корпуса достаточно определить абсциссу (х с) и аппликату (z c) центра величины; ординату центра величины (у с) не рассчитывают.
Общие выражения, определяющие зависимости х с и z c от характеристик теоретического чертежа даны выше – формулы (1.6) (1.8).


Правило трапеций позволяет получить расчетные зависимости для определения х с и z c. Исходя из (1.6) можно получить расчетную формулу
 ≃ ≃  , ,
| (1.29) |
| где | DL | – | теоретическая шпация; |
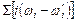
| – | исправленная сумма произведений номера шпангоута (i) на разницу площадей носового и кормового шпангоутов (при учете знака разницы), имеющих одинаковый номер (i и i ¢); | |
| S wi | – | исправленная сумма площадей шпангоутов. |
Для расчета х с может быть использована, в силу аналогии схемы, форма табл. 1.2 при замене ординат (уi) на площади шпангоутов (wi).
|
|
Известен и другой подход к определению хс. Исходя из общего выражения  по правилу трапеций, можно получить расчетную формулу
по правилу трапеций, можно получить расчетную формулу
 ≃ ≃ 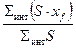 , ,
| (1.30) |
| где | Sинт (S·xf) | – | интегральная сумма произведений площади ватерлинии (S) на абсциссу ее центра тяжести (xf); |
| Sинт S | интегральная сумма площадей ватерлиний. |
Расчет х с по формуле (1.30) представлен в табл. 1.4, где, в частности, показана типовая схема определения интегральной суммы, на примере расчета 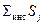 исходя из Sj.
исходя из Sj.
Здесь заметим, что интегральная сумма – это, по отношению к правилу трапеций, есть удвоенная исправленная сумма ряда значений показателя. особенностью формы табл. 1.4 также является то, что, наряду с буквенными обозначениями величин, используется их обозначение в виде числа-номера графы, заключенного в квадратные скобки.
 
| 
|
Для расчета аппликаты центра величины, исходя из зависимости общего вида (1.8), получена, с использованием правила трапеций, следующая формула
 ≃ ≃  , ,
| (1.31) |
| где | D T | – | интервал между плоскостями ватерлиний; |
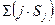
| – | исправленная сумма произведений номера ватерлинии (j) на ее площадь (Sj); | |

| – | исправленная сумма площадей ватерлиний. |
Расчет z c может быть выполнен по форме табл. 1.4; при этом используется формула
 ,
,
| где | 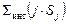
| – | интегральная сумма произведений номера ватерлинии (j) на ее площадь (Sj); |

| – | интегральная сумма площадей ватерлиний. |
Плавучесть
Понятие плавучести.
|
|
|

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!