I признак подобия треугольников

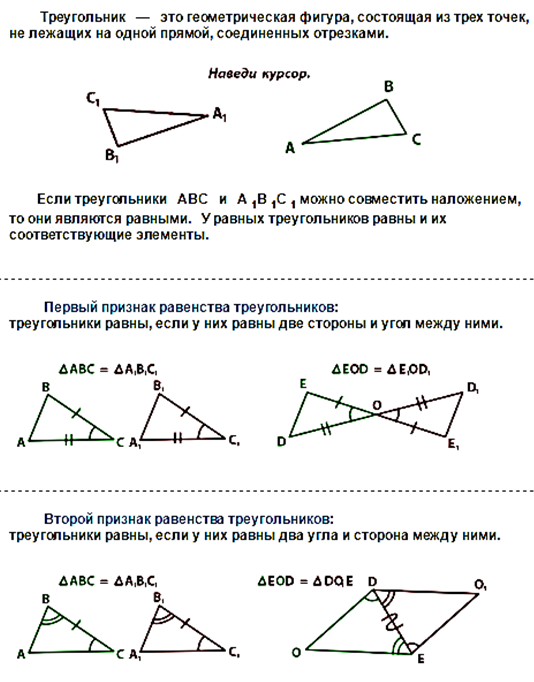
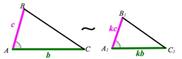Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

II признак подобия треугольников

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

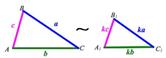III признак подобия треугольников

Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.

 

Свойства подобных треугольников

§ Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

 

 

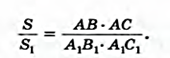
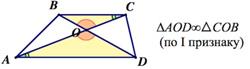Примеры наиболее часто встречающихся подобных треугольников

 

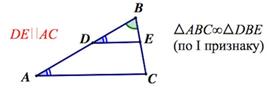1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.

 

2. Треугольники и, образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия –

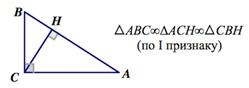
3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.

 

 

Билет № 8. Вопрос 1.

Алгебраическое выражение − это выражение, составленное из чисел и переменных с помощью знаков сложения, вычитания, умножения, деления, возведения в рациональную степень и извлечения корня и скобок. Простейшим алгебраическим выражением является одночлен.

Одночленом называется выражение, которое содержит числа, натуральные степени переменных и их произведения, и при этом не содержит никаких других действий с этими числами и переменными. Например, 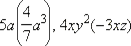− одночлены, а выражения 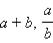− не одночлены.

Одночлен называется представленным в стандартном виде, если он представлен в виде произведения числового множителя на первом месте и степеней различных переменных. Числовой множитель у одночлена стандартного вида называется коэффициентом одночлена, сумму показателей степени переменных называют степенью одночлена. Ясно, что произведение одночленов также будет одночленом; ясно также, что одночлен в некоторой натуральной степени также является одночленом. Результаты таких действий (умножение одночленов и возведение одночлена в степень) обычно приводят к стандартному виду.

Пример 1

Привести к стандартному виду одночлены: 1) 2)

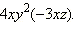
Решение 1) 2) 4 xy ²(–3 xz) = –12 x ² y ² z.

Два одночлена, приведённых к стандартному виду, называются подобными, если они совпадают или же отличаются только числовым коэффициентом. Сложение и вычитание подобных одночленов называется приведением подобных слагаемых.

Многочленом называется сумма одночленов. Если все одночлены в многочлене приведены к стандартному виду, то говорят, что это многочлен стандартного вида. Алгебраическое выражение, не содержащее операции деления и извлечения корня (такое выражение называется целым), всегда может быть приведено к многочлену стандартного вида. Степенью многочлена называется наибольшая из степеней его слагаемых.

Пример 3

Привести к многочлену стандартного вида (a – b)(a + b).

Решение

Имеем (a – b)(a + b) = (a – b) · a + (a – b) · b = a 2 – ba + ba – b 2 = a 2 – b 2.

Пример 4

Привести к многочлену стандартного вида (a ² – ab) – (3 ab – 2 a ² – 5 b (a + b ²)).

Решение

(a 2 – ab) – (3 ab – 2 a 2 – 5 b (a + b 2)) = a 2 – ab – 3 ab + 2 a 2 + 5 ba + 5 b 3 = 3 a 2 + ab + 5 b 3. Часто бывает полезно преобразовать многочлен так, чтобы он был представлен в виде произведения нескольких сомножителей. Такое тождественное преобразование называется разложением многочлена на множители. 1. Вынесение множителя за скобку. Из распределительного закона непосредственно следует, что ac + bc = c (a + b). Этим можно воспользоваться для вынесения множителя за скобки. 2. Использование формул сокращённого умножения. Формулы сокращённого умножения позволяют довольно эффективно представлять многочлен в форме произведения. a 2 – b 2 = (a + b)(a – b), (a + b)2 = a 2 + 2 ab + b 2, (a – b)2 = a 2 – 2 ab + b 2, a 3 + b 3 = (a + b)(a 2 – ab + b 2), a 3 – b 3 = (a – b)(a 2 + ab + b 2), (a + b)3 = a 3 + 3 a 2 b + 3 ab 2 + b 3, (a – b)3 = a 3 – 3 a 2 b + 3 ab 2 – b 3 3. Способ группировки. Этот способ заключается в том, что слагаемые многочлена можно сгруппировать различными способами на основе сочетательного и переместительного законов. На практике он применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку и исходный многочлен окажется представленным в виде произведения.

Билет № 8. Вопрос 2.

Окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности. Это расстояние называется радиус и в записях обозначается буквой R. Центр окружности обозначают буквой O.

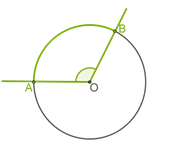Отрезки OA, OB, и OC — это радиусы, их длины равны. Отрезок BC, проходящий через центр окружности (круга) называется диаметром и обозначается буквой D. Диаметр разделяет окружность на две полуокружности и равен двум радиусам.

 

 

 

 

Билет № 9. Вопрос 1.

Билет № 9. Вопрос 2.

Билет № 10. Вопрос 1.

Дробное выражение - это математическое выражение, которое помимо действий сложения, вычитания и умножения, выполненных с числами и буквенными переменными, а также деления на число не равное нулю, содержит также деление на выражения с буквенными переменными.

Рациональные выражения - это все целые и дробные выражения. Рациональные уравнения - это уравнения, у которых левая и правые части являются рациональными выражениями. Если в рациональном уравнении левая и правая части будут являться целыми выражениями, то такое рациональное уравнение называется целым.

Если в рациональном уравнении левая или правая части будут являться дробными выражениями, то такое рациональное уравнение называется дробным.

Чтобы решить дробное уравнение, необходимо:

1. найти общий знаменатель дробей, входящих в уравнение;

2. умножить обе части уравнения на общий знаменатель;

3. решить получившееся целое уравнение;

4. исключить из его корней те, которые обращают в ноль общий знаменатель.

Билет № 10. Вопрос 2.

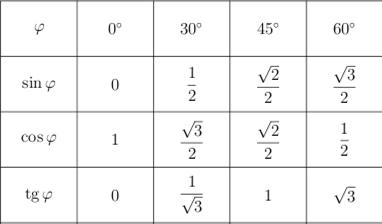
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается . Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .

Угол 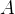обозначается соответствующей греческой буквой .

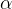Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.

Катеты — стороны, лежащие напротив острых углов.

Катет , лежащий напротив угла 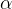, называется противолежащим (по отношению к углу 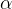). Другой катет 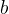, который лежит на одной из сторон угла 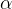, называется прилежащим.

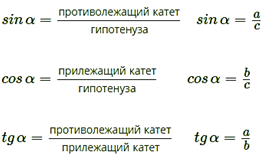
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:

 

 

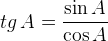
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.

 

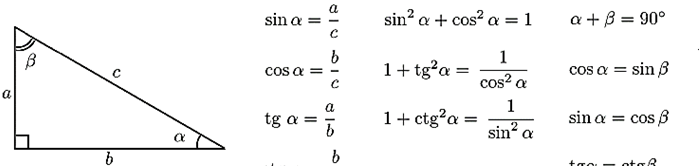
таблица значений синуса, косинуса, тангенса

 

Билет № 11. Вопрос 1.

Билет № 11. Вопрос 2.

В плоскости прямая и окружность могут пересекаться или не пересекаться. При пересечении могут иметь одну или две общие точки.

1. Если расстояние от центра окружности до прямой больше радиуса, то у прямой и окружности общих точек нет.

 

 

2. Если расстояние от центра окружности до прямой меньше радиуса, то у прямой и окружности две общие точки.

В этом случае прямую называют секущей окружности.

Если прямая имеет две общие точки с окружностью, то она называется секущей.

3. Если расстояние от центра окружности до прямой равна радиусу, то у прямой и окружности одна общая точка.

В этом случая прямую называют касательной к окружности.