

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Интересное:
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Лекция 11
Обратная матрица.
Обратная матрица. Теорема о ее единственности. Критерий существования обратной матрицы. Присоединенная матрица. Вычисление обратной матрицы с помощью присоединенной матрицы и с помощью элементарных преобразований. Матрица, обратная произведению двух обратимых матриц. Решение матричных уравнений вида AX = B и XA = B с невырожденной матрицей А. Формулы Крамера.
п.1. Обратная матрица и ее свойства
Определение 11.1. Пусть A — квадратная матрица порядка п. Квадратную матрицу B того же порядка называют обратной к A, если AB = BA = E, где E — единичная матрица порядка п.
Обратную матрицу обозначают A-1. Она позволяет определить целую отрицательную степень матрицы A.
А именно, для п > 0 полагают ЕA-n = (A-1)n.
Из определения следует, что если матрица В - обратная к матрице А, то матрица А - обратная к матрице В. Поэтому А и В – взаимообратные.
Теорема 11.1. Если квадратная матрица А имеет обратную матрицу, то обратная матрица единственная.
◄ Предположим, что матрица A имеет две обратные матрицы В и В1. Тогда, согласно определению 11.1 обратной матрицы, выполнены, в частности, равенства AB1 = E и BA = E. Используя ассоциативность умножения матриц, получаем B = BE = В (AB1) = (BA)B1 = EB' = B1, т.е. матрицы B и B1 совпадают. ►
Квадратная матрица не всегда имеет обратную. Установить, имеет ли данная матрица обратную, позволяет следующий критерий.
Теорема 11.2. Для того чтобы квадратная матрица A порядка п имела обратную, необходимо и достаточно, чтобы det A  0.
0.
◄ Необходимость. Дано: квадратная матрица A порядка п имеет обратную A-1.
Доказать: det A  0.
0.
Доказательство необходимости. По условию, A-1 — матрица, обратная к А. Тогда det(AA-1) = detE = 1. По, свойству определителей имеем:
|
|
det(AA-1) = det A det A-1. Поэтому det A det A-1 = 1 и, следовательно,
det A  0.
0.
◄ Достаточность. Дано: det A  0. Доказать: квадратная матрица A порядка п имеет обратную A-1.
0. Доказать: квадратная матрица A порядка п имеет обратную A-1.
Доказательство достаточности.
Обозначим через Aij алгебраическое дополнение матрицы А, соответствующее элементу aij, т.е. Aj = (—1)i+jMij, где Mij — минор этого же элемента.
Раскрывая определитель матрицы A по i-й строке, получаем равенство


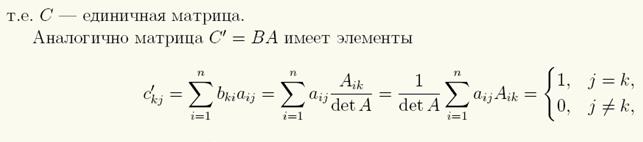
следовательно, матрица С' также является единичной.
Согласно определению 11.1, матрица B является обратной для A:
B = A-1. ►
Следствие 11.1. Если квадратная матрица A имеет обратную, то
det A-1 = (det A)-1.
◄ Действительно, det A-1 det A = det(A-1A) = det E =1. ►
Квадратную матрицу с ненулевым определителем называют невырожденной или неособой. В противном случае, когда определитель матрицы равен нулю, ее называют вырожденной. Итак, для существования обратной матрицы A-1 необходимо и достаточно, чтобы матрица A была невырожденной.
Теорема 11.3. Если квадратные матрицы A и B порядка n имеют обратные матрицы, то и их произведение имеет обратную матрицу, причем (AB)-1 = B-1A-1.
◄ В соответствии с определением 11.1 обратной матрицы достаточно доказать два равенства: (AB)B-1A-1 = E, (B-1A-1)(AB) = E. Используя ассоциативность умножения матриц, получаем
(AB)(B-1A-1) = A(BB-1)A-1 = AEA-1 = AA-1 = E,
(B-1A-1)(AB) = B-1(A-1A)B = B-1EB = B-1B = E. ►
Теорема 11.4. Если матрица A порядка n имеет обратную, то и транспонированная матрица AT имеет обратную, причем (AT)-1 = (A-1)T.
Нужно убедиться, что  и
и  . Используя свойство произведения матриц относительно операции транспонирования, имеем
. Используя свойство произведения матриц относительно операции транспонирования, имеем
AT(A-1)T = (A-1A)T = ET = E, (A-1)TAT = (AA-1)T = ET = E.

Лемма
1) Произведение обратимых матриц - обратимая матрица
2) Если А - обратима, то обратная к ней,  , обратима, и
, обратима, и  .
.
3) Единичная матрица Е обратима, и  .
.
Обозначение. Множество всех обратимых матриц порядка n над полем Р обозначается 
П.2. Элементарные матрицы.
Пусть Р = (Р, +, ·, -, 0, 1)-поле скаляров.
Определение. Элементарной матрицей называется матрица, полученная из единичной матрицы Е в результате одного из следующих элементарных преобразований:
|
|
1) Умножение одной строки(столбца) матрицы Е на скаляр  ≠0.
≠0.
2) Прибавление к какой-либо строке матрицы Е другой строки, умноженной на скаляр  .
.
Обозначение.  - элементарная матрица, полученная умножением на
- элементарная матрица, полученная умножением на  стоки (столбца) матрицы Е.
стоки (столбца) матрицы Е.
 - элементарная матрица, полученная прибавлением к i -ой строке (столбцу) матрицы Е j -ой стоки(столбца), умноженной на
- элементарная матрица, полученная прибавлением к i -ой строке (столбцу) матрицы Е j -ой стоки(столбца), умноженной на  .
.
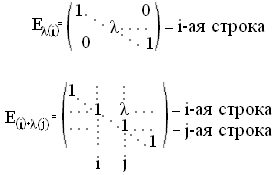
Пример. Элементарные матрицы порядка
n=2: 

Обозначение.  - элементарная матрица, полученная из Е элементарным преобразованием
- элементарная матрица, полученная из Е элементарным преобразованием 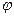 .
.
Свойства обратимости
Пример 3.
Найти обратную матрицу  , используя формулу:
, используя формулу: 
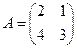 .
.
Решение.
Вычислим определитель матрицы:
 ,
,
Найдем присоединенную матрицу по формуле:
 , где
, где  - алгебраическое дополнение элемента
- алгебраическое дополнение элемента  .
.
 .
.
Тогда
 .
.
Пример 4. Найти обратную матрицу  , используя формулу:
, используя формулу:  ,
,
 .
.
Решение. Найдем определитель матрицы:
 ;
;
Вычислим алгебраические дополнения:
 ;
; 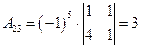 ;
;
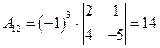 ;
;  ;
;
 ;
;  ;
;
 ;
;  ;
;
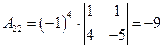 ;
;
Тогда
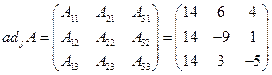 .
.
Следовательно
 .
.
Пример 5. Найти обратную матрицу  , используя формулу:
, используя формулу:  ,
,

Решение. Найдем определитель матрицы:
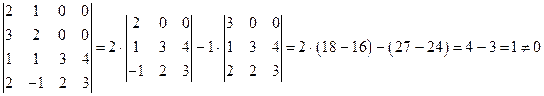 ;
;
 ;
;  ;
;
 ;
;  ;
;
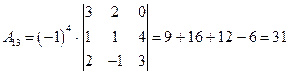 ;
; 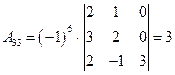 ;
;
 ;
;  ;
;
 ;
;  ;
;
 ;
;  ;
;
 ;
; 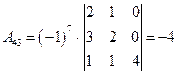 ;
;
 ;
;  ;
;
 ;
;
 .
.
Для самостоятельного решения.
Найти обратную матрицу  , используя формулу:
, используя формулу: 
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6) 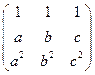 ;
;
7)  ; 8)
; 8) 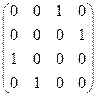 ;
;
9) 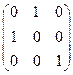 ;
;
10)  11)
11)  ;
;
12)  ; 13)
; 13)  ;
;
Решение.
 .
.
1) 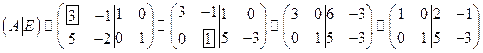


 ,
,



 ,
,
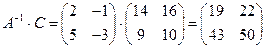 ,
,
 .
.
2)  .
.
Решение.



 ,
,



 ,
,
 ,
,
 .
.
Для самостоятельного решения:
3)  ;
;
4)  ;
;
5)  ;
;
6)  .
.
П.7. Правило Крамера.
Пусть Р = (Р, +, ·, -, 0, 1)- поле скаляров.

 ;
;
 ;
;
 -столбец свободных членов.
-столбец свободных членов.
 - алгебраическое дополнение
- алгебраическое дополнение  .
. 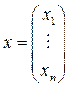
Теорема 1. Если определитель матрицы А не равен нулю, то система (1) имеет единственное решение, которое задаётся равенствами:
|
|


где матрица  получена из матрицы А заменой i -ого столбца столбцом свободных членов.
получена из матрицы А заменой i -ого столбца столбцом свободных членов.
Доказательство. Запишем систему (1) в матричной форме:
 ; по условию
; по условию  , значит матрица А – обратима, тогда
, значит матрица А – обратима, тогда 
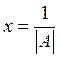
 .
.  =
= 
Формулы (2) называются формулами Крамера. ■
Пример 1. Найти решение системы по правилу Крамера.


 ,
,  .
.
 ,
, 
 ,
, 
Ответ: 
Пример 2. Решить системы уравнений по правилу Крамера:
1) 
Решение.
1) Найдем определитель системы:
 Вычислим определители, заменяя столбцом свободных членов поочередно столбцы основного определителя:
Вычислим определители, заменяя столбцом свободных членов поочередно столбцы основного определителя:
 ;
;
 ;
;
 ;
;
 ;
;

Получим  .
.
Ответ: 
Для самостоятельного решения 2) – 5).
2) 
3) 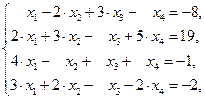
4) 
5) 
Пример.

r=1: 
r=2: 
Теорема. Ранг ненулевой матрицы А равен наибольшему из порядков ненулевых миноров матрицы А.
Доказательство. Так как А - ненулевая матрица, А ≠0, то она имеет некоторый ранг  Докажем что А имеет хотя бы один ненулевой минор порядка r.
Докажем что А имеет хотя бы один ненулевой минор порядка r.  , значит матрица А имеет r линейно независимых строк. Пусть В - матрица порядка
, значит матрица А имеет r линейно независимых строк. Пусть В - матрица порядка  , состоящая из r ненулевых строк матрицы А.
, состоящая из r ненулевых строк матрицы А.  значит В имеет r линейно независимых столбцов. Пусть С - матрица, состоящая из r линейно независимых столбцов матрицы В, тогда её размерность
значит В имеет r линейно независимых столбцов. Пусть С - матрица, состоящая из r линейно независимых столбцов матрицы В, тогда её размерность 
 .
.
По теореме 2 п.3 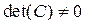 , так как столбцы С линейно независимы. Значит
, так как столбцы С линейно независимы. Значит  есть ненулевой минор порядка r матрицы А.
есть ненулевой минор порядка r матрицы А.
Пусть М - минор порядка  матрицы А. При
матрицы А. При  любые k -строк матрицы А линейно зависимы. Поэтому линейно зависимы строки любой квадратной матрицы
любые k -строк матрицы А линейно зависимы. Поэтому линейно зависимы строки любой квадратной матрицы  , подматрицы матрицы А. Тогда по теореме 1 п. 3 равен нулю любой минор порядка
, подматрицы матрицы А. Тогда по теореме 1 п. 3 равен нулю любой минор порядка  матрицы А. ■
матрицы А. ■
Лекция 11
Обратная матрица.
Обратная матрица. Теорема о ее единственности. Критерий существования обратной матрицы. Присоединенная матрица. Вычисление обратной матрицы с помощью присоединенной матрицы и с помощью элементарных преобразований. Матрица, обратная произведению двух обратимых матриц. Решение матричных уравнений вида AX = B и XA = B с невырожденной матрицей А. Формулы Крамера.
п.1. Обратная матрица и ее свойства
Определение 11.1. Пусть A — квадратная матрица порядка п. Квадратную матрицу B того же порядка называют обратной к A, если AB = BA = E, где E — единичная матрица порядка п.
|
|
Обратную матрицу обозначают A-1. Она позволяет определить целую отрицательную степень матрицы A.
А именно, для п > 0 полагают ЕA-n = (A-1)n.
Из определения следует, что если матрица В - обратная к матрице А, то матрица А - обратная к матрице В. Поэтому А и В – взаимообратные.
Теорема 11.1. Если квадратная матрица А имеет обратную матрицу, то обратная матрица единственная.
◄ Предположим, что матрица A имеет две обратные матрицы В и В1. Тогда, согласно определению 11.1 обратной матрицы, выполнены, в частности, равенства AB1 = E и BA = E. Используя ассоциативность умножения матриц, получаем B = BE = В (AB1) = (BA)B1 = EB' = B1, т.е. матрицы B и B1 совпадают. ►
Квадратная матрица не всегда имеет обратную. Установить, имеет ли данная матрица обратную, позволяет следующий критерий.
Теорема 11.2. Для того чтобы квадратная матрица A порядка п имела обратную, необходимо и достаточно, чтобы det A  0.
0.
◄ Необходимость. Дано: квадратная матрица A порядка п имеет обратную A-1.
Доказать: det A  0.
0.
Доказательство необходимости. По условию, A-1 — матрица, обратная к А. Тогда det(AA-1) = detE = 1. По, свойству определителей имеем:
det(AA-1) = det A det A-1. Поэтому det A det A-1 = 1 и, следовательно,
det A  0.
0.
◄ Достаточность. Дано: det A  0. Доказать: квадратная матрица A порядка п имеет обратную A-1.
0. Доказать: квадратная матрица A порядка п имеет обратную A-1.
Доказательство достаточности.
Обозначим через Aij алгебраическое дополнение матрицы А, соответствующее элементу aij, т.е. Aj = (—1)i+jMij, где Mij — минор этого же элемента.
Раскрывая определитель матрицы A по i-й строке, получаем равенство


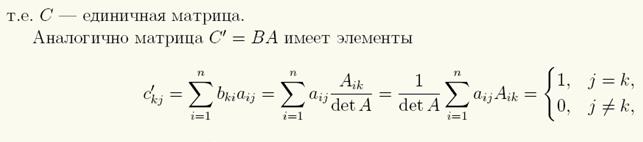
следовательно, матрица С' также является единичной.
Согласно определению 11.1, матрица B является обратной для A:
B = A-1. ►
Следствие 11.1. Если квадратная матрица A имеет обратную, то
det A-1 = (det A)-1.
◄ Действительно, det A-1 det A = det(A-1A) = det E =1. ►
Квадратную матрицу с ненулевым определителем называют невырожденной или неособой. В противном случае, когда определитель матрицы равен нулю, ее называют вырожденной. Итак, для существования обратной матрицы A-1 необходимо и достаточно, чтобы матрица A была невырожденной.
Теорема 11.3. Если квадратные матрицы A и B порядка n имеют обратные матрицы, то и их произведение имеет обратную матрицу, причем (AB)-1 = B-1A-1.
◄ В соответствии с определением 11.1 обратной матрицы достаточно доказать два равенства: (AB)B-1A-1 = E, (B-1A-1)(AB) = E. Используя ассоциативность умножения матриц, получаем
(AB)(B-1A-1) = A(BB-1)A-1 = AEA-1 = AA-1 = E,
(B-1A-1)(AB) = B-1(A-1A)B = B-1EB = B-1B = E. ►
Теорема 11.4. Если матрица A порядка n имеет обратную, то и транспонированная матрица AT имеет обратную, причем (AT)-1 = (A-1)T.
Нужно убедиться, что  и
и  . Используя свойство произведения матриц относительно операции транспонирования, имеем
. Используя свойство произведения матриц относительно операции транспонирования, имеем
|
|
AT(A-1)T = (A-1A)T = ET = E, (A-1)TAT = (AA-1)T = ET = E.

Лемма
1) Произведение обратимых матриц - обратимая матрица
2) Если А - обратима, то обратная к ней,  , обратима, и
, обратима, и  .
.
3) Единичная матрица Е обратима, и  .
.
Обозначение. Множество всех обратимых матриц порядка n над полем Р обозначается 
П.2. Элементарные матрицы.
Пусть Р = (Р, +, ·, -, 0, 1)-поле скаляров.
Определение. Элементарной матрицей называется матрица, полученная из единичной матрицы Е в результате одного из следующих элементарных преобразований:
1) Умножение одной строки(столбца) матрицы Е на скаляр  ≠0.
≠0.
2) Прибавление к какой-либо строке матрицы Е другой строки, умноженной на скаляр  .
.
Обозначение.  - элементарная матрица, полученная умножением на
- элементарная матрица, полученная умножением на  стоки (столбца) матрицы Е.
стоки (столбца) матрицы Е.
 - элементарная матрица, полученная прибавлением к i -ой строке (столбцу) матрицы Е j -ой стоки(столбца), умноженной на
- элементарная матрица, полученная прибавлением к i -ой строке (столбцу) матрицы Е j -ой стоки(столбца), умноженной на  .
.
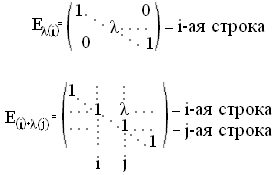
Пример. Элементарные матрицы порядка
n=2: 

Обозначение.  - элементарная матрица, полученная из Е элементарным преобразованием
- элементарная матрица, полученная из Е элементарным преобразованием 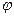 .
.
Свойства элементарных матриц.
1) Любая элементарная матрица обратима.
2) Произведение элементарных матриц является обратимым.
Доказательство. Очевидно: элементарная матрица являются обратимой, а произведение обратимых матриц - обратимо.
3) Пусть 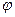 -элементарное преобразование 1-го или 2-го вида,
-элементарное преобразование 1-го или 2-го вида,  . Если матрица В получается из матрицы А элементарным преобразованием
. Если матрица В получается из матрицы А элементарным преобразованием 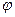 , то
, то 
4) Если матрица С получена из матрицы А цепочкой элементарных преобразований вида 1 и 2  , то С =
, то С =  .
.
|
|
|

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!