В начале главы упоминалось о том, что в результате ДПФ гармонической функции на практике получаются две гармоники. Однако этот эмпирический факт не доказывался. Докажем теперь строго, какие гармоники дает произвольная гармоническая функция f(t) = A cos(2πtm / T + φ) при целочисленном m 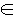 [0, N[.
[0, N[.
Напомним формулу прямого ДПФ:

В данном случае
xn = f(tn) = f(Tn / N) = A cos(2πTnm / NT + φ) = A cos(2πnm / N + φ)
Введем обозначения:
wn = 2πn / N
Zk,n = (f(tn) / A) e-j2πkn / N = cos(wnm + φ) e-jwnk
В результате формула прямого ДПФ упрощается до:
Xk = A  Zk,n
Zk,n
Теперь преобразуем Zk,n:
Zk,n = cos(wnm + φ) e-jwnk =
применяем формулу Эйлера:
= cos(wnm + φ) (cos(-wnk) + j sin(-wnk)) =
= cos(wnm + φ) (cos(wnk) - j sin(wnk)) =
раскрываем скобки:
= cos(wnm + φ) cos(wnk) - j cos(wnm + φ) sin(wnk) =
применяем формулы произведения косинусов и синуса на косинус:
= (1/2)[cos((wnm + φ) - wnk) + cos((wnm + φ) + wnk)] -
= - (j/2)[sin(wnk - (wnm + φ)) + sin(wnk + (wnm + φ))] =
перегруппировываем слагаемые:
= (1/2)[cos((wnm + φ) - wnk) + cos((wnm + φ) + wnk) -
- j sin(wnk - (wnm + φ)) - j sin(wnk + (wnm + φ))] =
= (1/2)[cos((wnm + φ) - wnk) + cos((wnm + φ) + wnk) +
+ j sin((wnm + φ) - wnk) - j sin((wnm + φ) + wnk)] =
= (1/2)[cos(wnm + φ - wnk) + j sin(wnm + φ - wnk) +
+ cos(wnm + φ + wnk) - j sin(wnm + φ + wnk)] =
применяем формулу Эйлера (только наоборот):
= (1/2)[e j(wnm + φ - wnk) + e -j(wnm + φ + wnk)] =
и выносим за скобки все, что можно:
= (1/2)[e jφe jwn(m - k) + e -jφe -jwn(m + k)]
Теперь подставляем полученные величины в сумму ДПФ и преобразуем:
Xk = A  Zk,n =
Zk,n =
= A  (1/2)[e jφe jwn(m - k) + e -jφe -jwn(m + k)] =
(1/2)[e jφe jwn(m - k) + e -jφe -jwn(m + k)] =
= (A/2)e jφ  e jwn(m - k) + (A/2)e -jφ
e jwn(m - k) + (A/2)e -jφ  e -jwn(m + k) =
e -jwn(m + k) =
подставляем wn:
= (A/2)e jφ  e j2πn(m - k) / N + (A/2)e -jφ
e j2πn(m - k) / N + (A/2)e -jφ  e -j2πn(m + k) / N =
e -j2πn(m + k) / N =
вводим обозначения для сумм:
= (A/2)e jφS1 + (A/2)e -jφS2
Легко видеть, что суммы S1 и S2 являются геометрическими прогрессиями, а формула суммы геометрической прогрессии нам известна:
SN = a0(qN - 1) / (q - 1), q ≠ 1 (34)
Первый элемент прогрессии в обоих случаях равен a0 = 1.
Знаменатели прогрессий равны
q1 = e j2π(m - k) / N для S1
и
q2 = e -j2π(m + k) / N для S2.
Условие q ≠ 1 вынуждает нас решить уравнения:
e j2π(m - k) / N = 1,
и
e -j2π(m + k) / N = 1,
Учитывая Теорему 0, получим, что условие q ≠ 1 не выполняется при k = m для S1 и при k = (N - m) для S2.
В случае, когда выполняются оба условия: k = m и k = (N - m), то есть k = m = N /2 обе суммы нельзя считать по формуле геометрической прогресии.
В случае k = m для S1 придется выполнить небольшие дополнительные преобразования:
S1 =  e j2πn(m - m) / N =
e j2πn(m - m) / N =  1 = N
1 = N
Аналогично в случае k = N - m для S2:
S2 =  e -j2πn(m + N - m) / N =
e -j2πn(m + N - m) / N =  e -j2πn =
e -j2πn =  1 = N
1 = N
В случае k = m = N / 2 имеем:
Xk = (A/2)Ne jφ + (A/2)Ne -jφ =
= (A/2)N(e jφ + e -jφ) =
= (A/2)N(cos φ + j sin φ + cos φ - j sin φ) =
= (A/2)N(2 cos φ) =
= ANcos φ
В случае k = m = 0 имеем:
Xk = (A/2)e jφN + (A/2)e -jφN = (A/2)N(e jφ + e -jφ) =
= (A/2)N(cos φ + jsin φ + cos φ - jsin φ) = ANcos φ
Наконец, получаем формулу для Xk:
Для k = m = N / 2 или k = m = 0:
Xk = ANcos φ
Для k = m ≠ N / 2:
Xk = (A/2)Ne jφ + (A/2)e -jφ(e -j4πm - 1) / (e -j4πm / N - 1)
Для k = (N - m) ≠ N / 2:
Xk = (A/2)e jφ(e j4πm - 1) / (e j4πm / N - 1) + (A/2)Ne -jφ
Для остальных k:
Xk = (A/2)e jφ(e j2π(m - k) - 1) / (e j2π(m - k) / N - 1) +
+ (A/2)e -jφ(e -j2π(m + k) - 1) / (e -j2π(m + k) / N - 1) (35)
Заметим, что эта формула получена без использования факта целочисленности m и k.
Теперь учтем целочисленность. Для этого применим Теорему 0 и заменим в формуле (35) экспоненты на 1 везде, где выполняется это условие:
Для k = m = N / 2 или k = m = 0:
Xk = ANcos φ
Для k = m ≠ N / 2:
Xk = (A/2)Ne jφ + (A/2)e -jφ(1 - 1) / (e -j4πm / N - 1)
Для k = (N - m) ≠ N / 2:
Xk = (A/2)e jφ(1 - 1) / (e j4πm / N - 1) + (A/2)Ne -jφ
Для остальных k:
Xk = (A/2)e jφ(1 - 1) / (e j2π(m - k) / N - 1) +
+ (A/2)e -jφ(1 - 1) / (e -j2π(m + k) / N - 1)
Сокращаем везде, где получаются нули, и приходим к формулам:
Для k = m = N / 2 или k = m = 0:
Xk = ANcos φ
Для k = m ≠ N / 2:
Xk = (A/2)Ne jφ
Для k = (N - m) ≠ N / 2:
Xk = (A/2)Ne -jφ
Для остальных k:
Xk = 0 (36)
Вывод:



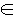 [0, N[.
[0, N[.
 Zk,n
Zk,n


