Шаг 0. Пусть источники помечены но не просмотрены, а все остальные узлы не помечены.
Шаг 1. Выбрать любой помеченный, но не просмотренный узел i.
Шаг 2. Просмотреть все дуги e (i, j) с пропускной способностью a е > 0, соединяющие узел i с еще не помеченными узлами j. Приписать пометки узлам j и отметить дуги e j = e = (i, j).Теперь узел i помечен и просмотрен, узлы j помечены, но не просмотрены. Если при этом сток оказался помеченным, то необходимая цепь найдена. В противном случае после просмотра по всем дугам (i, j) перейти к шагу 3.
Шаг 3. Пусть узел i помечен и просмотрен. Перейти к шагу 1 и повторять шаги алгоритма до тех пор, пока не останется помеченных и не просмотренных узлов. На этом поиск максимального потока заканчивается.
Рассмотрим пример.

 7.7 I
7.7 I


 c e
c e


 16 I 9.8 I 12 7 I
16 I 9.8 I 12 7 I


 I 8.8 I d I
I 8.8 I d I


 s a I 11 I j
s a I 11 I j





 12.1 12 I 5
12.1 12 I 5
 f
f
 6.2 I 11 I 15 I 20 I
6.2 I 11 I 15 I 20 I
I


 b t
b t
I
Обозначено: I - ресурсы не использованы
R - ресурсы использованы полностью
IR - ресурсы использованы частично
1. Выбираем какой - то один из произвольных потоков.
p1 = min {f(s, b), f(b, t)} = min {6.2; 8} = 6.2;

 I
I



 c e
c e

 I
I
 I I d I
I I d I
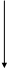


 I
I


 s a I j
s a I j


 I I I
I I I


 f
f
R I I

 I
I
 b t
b t
IR
2. Маршрут (s, a), (a, f), (f, t);
p2 = min {f(s, a), f(a, f), f(f, t)} = min {12.1; 12; 15} = 12;
PS[AK1] = 18.2;

 I
I



 c e
c e

 I
I
 I I d I
I I d I
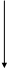


 I
I

 s a I j
s a I j



 IR R I
IR R I

 f
f
 R I I IR I
R I I IR I


 b t IR
b t IR
3. Маршрут (s,a), (a,b), (b,f), (f,t);
p3 = min {f(s,a), f(a,b), f(b,f), f(f,t)} = min {0.1; 11; 7.5; 3} = 7.5;
PS = 18.3;

 I
I


 c e
c e


 I
I
 I I d I
I I d I
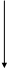


 I
I

 s a I j
s a I j



 IR R I
IR R I
 f
f

 R IR IR I
R IR IR I


 R
R
B t
IR
4.Маршрут (s, a), (a, b), (b, t);
p4 = min {f(s, c), f(c, e), f(e, j), f(j, t)} = min {16; 7.7; 7, 20} = 7;
PS = 25.3;

 I
I


 c e
c e


 I
I
 I I d I
I I d I
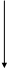


 I
I

 s a I j
s a I j



 IR R I
IR R I

 f
f
 R IR IR I
R IR IR I


 R в t
R в t
R
Таким образом, максимальный поток составит 25.3 единицы.
Если для сети каждое ребро характеризуется некоторым числом, которое является расстоянием между узлами сети, то возникает задача определения кратчайшего расстояния между заданными узлами, которые называются истоком и стоком
Рассмотрим алгоритм Дейкстры для определения кратчайшего пути (цепи) из истока в сток.
Шаг 0. Выбрать в качестве перспективного множество узлов множество S c = S 0 и положить d i = 0 для i ÎS 0 и d i = ¥ для i Ï S 0.
Шаг 1. Выбрать узел i * Î S c, которому соответствует наименьшее значение d i (i Î S 0). Найденная таким образом величина d i соответствует кратчайшему пути из некоторого источника в узел i* (длиной дуги является c e), а дуга e i (определенная для всех узлов i Î S c, кроме источников) есть последняя дуга пути. Если i * - сток, то процедура поиска кратчайшего пути заканчивается.
Шаг 2. Просмотреть дуги e = (i *, j) и заменить отметку d j на min {d j, d i + c e}. Если d j была равна ¥, ввести узел j в S c. Eсли d j уменьшилась, ввести обозначение e j = e = (i*, j).
Шаг 3. Удалить i* из S c и перейти к шагу 1, если множество S c не пусто. На этом поиск кратчайшего пути заканчивается.
Рассмотрим пример.
Для сети, показанной на рисунке, определить кратчайший путь из истока в сток.

 7.7
7.7


 c e
c e


 16 9.8 d 12 7
16 9.8 d 12 7

 8.8
8.8




 s a 5 j
s a 5 j




 исток 12.1
исток 12.1
 12 f 11
12 f 11

6.2 7.5 15 20



 b t
b t
Сток
1. Окрасим вершину s.
Положим d(s) = 0;
d(a) = d(b) = d(c) = d(e) =d(f) = d(j) =¥;
2. Текущая переменная y = s;
d(a) = min { d(a), d(s) + d(s,a)} = min {¥; 0 + 12.1} = 12.1;
d(b) = min {d(b), d(s) + d(s,b)} = min {¥; 0 + 6.2} = 6.2;
d(c) = min {d(c), d(s) + d(s,c)} = min {¥; 0 + 16 } = 16;
d(d) = min {d(d), d(s) + d(s,d)} = min {¥; 0 + ¥ } = ¥;
d(e) = min {d(e), d(s) + d(s,e)} = min {¥; 0 + ¥ } = ¥;
d(f) = min {d(f), d(s) + d(s,f)} = min {¥; 0 + ¥ } = ¥;
d(j) = min {d(j), d(s) + d(s,j)} = min {¥; 0 + ¥ } = ¥;
d(t) = min {d(t), d(s) + d(s,t)} = min {¥; 0 + ¥ } = ¥;
min {d(a), d(b), d(c), d(d), d(e), d(f), d(j),d(t)} =
= min {12.1; 6.2; 16; ¥; ¥; ¥; ¥; ¥} = 6.2; d(b) = 6.2;
Окрашиваем вершину b.

 s
s

b
3. Текущая переменная y = b;
d(a) = min {d(a), d(b) + d(b,a)} = min {12.1; 6.2 + ¥} = 12.1;
d(c) = min {d(c), d(b) + d(b,c)} = min {16; 6.2 + ¥} = 16;
d(d) = min {d(d), d(b) + d(b,d)} = min {¥; 6.2 + ¥} = ¥;
d(e) = min {d(e), d(b) + d(b,e) } = min {¥; 6.2 + ¥} = ¥;
d(f) = min {d(f), d(b) + d(b,f) } = min {¥; 6.2 + 7.5} = 13.7;
d(j) = min {d(j), d(b) + d(b,j) } = min {¥; 6.2 + ¥} = ¥;
d(t) = min {d(t), d(b) + d(b,t) } = min {¥; 6.2 + 8} = 14.2;
min {d(a), d(c), d(d), d(e), d(f0, d(j),d(t)} =
= min {12.1; 16; ¥; ¥; 13.7; ¥; ¥} = 12.1; d(a) = 12.1;
Окрашиваем вершину a.


 s a
s a


b
4. Текущая переменная y = a;
d(c) = min {d(c), d(a) + d(a,c)} = min {16; 12.1 + 9.8} = 16;
d(d) = min {d(d), d(a) + d(a,d)} = min {¥; 12.1 + 8.8} = 20.9;
d(e) = min {d(e), d(a) + d(a,e)} = min {¥; 12.1 + ¥} = ¥;
d(f) = min {d(f), d(a) + d(a,f)} = min {13.7; 12.1 + 12} = 13.7;
d(j) = min {d(j), d(a) + d(a,j)} = min {¥; 12.1 +¥} = ¥;
d(t) = min {d(t), d(b)+d(b,t)} = min {¥; 12.1 + ¥, 6.2+8} = 14.2;
min {d(c), d(d), d(e), d(f), d(j),d(t)} =
= min {16; 20.9; ¥; 13.7; ¥; ¥} =13.7; d(f) = 13.7;
Окрашиваем вершину f.



 s a
s a


 f
f
b
5. Текущая переменная y = f;
d(c) = min {d(c), d(f) + d(f,c)} = min {16; 13.7 + ¥} = 16;
d(d) = min {d(d), d(f) + d(f,d)} = min {20.9; 13.7 + ¥} = 20.9;
d(e) = min {d(e), d(f) + d(f,e)} = min {¥; 13.7 + ¥} = ¥;
d(j) = min {d(j), d(f) + d(f,j)} = min {¥; 13.7 +11} = 24.7;
d(t) = min {d(t), d(f) + d(f,t), d(b)+d(b,t)} = min {¥; 13.7 + 15, 6.2+8} = 14.2;
min {d(c), d(d), d(e), d(j), d(t)} = min {16; 20.9; ¥; 24.7; 14.2} = =14.2;
d(t) = 14.2.
Окрашиваем вершину t.
Вывод: Кратчайший путь из истока s в сток t только один,
состоит из дуг (s,b) и (b,t) и равен 14.2 единиц.
Рассмотренные положения по теории графов могут использоваться при решении задач моделирования объектов со сложной внутренней структурой. Алгоритмы, построенные с использованием теории графов, отличаются высоким быстродействием, а модели объектов и процессов получаются наглядными и простыми в программировании.
[AK1]






 7.7 I
7.7 I

 c e
c e



 I 8.8 I d I
I 8.8 I d I

 s a I 11 I j
s a I 11 I j




 12.1 12 I 5
12.1 12 I 5 f
f 6.2 I 11 I 15 I 20 I
6.2 I 11 I 15 I 20 I





 c e
c e
 I
I I I d I
I I d I
 I
I

 s a I j
s a I j

 I I I
I I I


 b t
b t





 R I I IR I
R I I IR I b t IR
b t IR



 IR R I
IR R I
 R IR IR I
R IR IR I




 R IR IR I
R IR IR I

 7.7
7.7

 c e
c e

 16 9.8 d 12 7
16 9.8 d 12 7



 s a 5 j
s a 5 j



 исток 12.1
исток 12.1 12 f 11
12 f 11

 b t
b t
 s
s


 s a
s a



