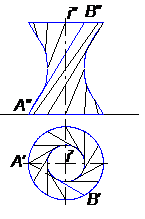Символика и принятые обозначения

КОНСПЕКТ ЛЕКЦИЙ ДИСЦИПЛИНЫ

«НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ. ИНЖЕНЕРНАЯ ГРАФИКА»

 

Направление подготовки: 250100 Лесное дело

Профили: Лесное хозяйство

Кафедра: Механики и инженерной графики

Квалификация (степень) выпускника: бакалавр

Форма обучения: очная

Курс 1; Семестр 2

 

Кинель 2013

Лекция 1

Тема: Символика и принятые обозначения. Чертеж Монжа. Образование чертежа на 2-х плоскостях проекций. Точка, прямая, плоскость, поверхность на чертеже. Классификация. Конкурирующие точки.

План лекции

 

1. Символика и принятые обозначения.

2. Образование чертежа на 2-х плоскостях проекций. Эпюр Монжа.

3. Конкурирующие точки.

4. Прямая на чертеже. Классификация прямых.

5. Плоскость на чертеже. Классификация плоскостей.

6. Поверхность на чертеже. Гранные поверхности. Поверхности вращения.

 

Символика и принятые обозначения

Целью начертательной геометрии является изучение пространственных форм объектов окружающего нас мира и взаимоотношений этих форм, познание соответствующих закономерностей и применение их к решению практических задач.

Основным средством изучения геометрических свойств предметов в начертательной геометрии является изображение этих предметов.

Изображение, полученное при помощи операции проецирования, называется проекцией предмета. Проекционное изображение, по которому можно восстановить предмет, является чертежом. Чертеж отличается от других изображений тем, что он построен по правилам начертательной геометрии и в соответствии с этими правилами позволяет определять геометрические свойства изображенного предмета.

 

ПРИНЯТЫЕ ОБОЗНАЧЕНИЯ

1. Точки в пространстве – прописными буквами латинского алфавита А,В,С,…, а также цифрами;

2. Линии в пространстве – строчными буквами латинского алфавита a,b,c,…

3. Плоскости – строчными буквами греческого алфавита

4. Плоскости проекций: произвольная плоскость - ,

горизонтальная – ;

фронтальная – ;

профильная – ;

любая дополнительная - .

5. Оси проекций - x, y, z.

6. Начало координат – прописной буквой О.

7. Проекции точек: на горизонтальную плоскость - А′, В′, С′,…;

на фронтальную плоскость - А′′, В′′, С′′,…;

на профильную плоскость - А′′′, В′′′, С′′′;

на произвольную плоскость - А⁰, В⁰, С⁰,…

на дополнительную плоскость - А^IV, В^IV, С^IV,…

8. Обозначение плоскостей заданных следами:

горизонтальный след плоскости ;

фронтальный след плоскости ;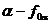

профильный след плоскости .

9. Для проецирующих плоскостей:

- горизонтально - проецирующая плоскость;

- фронтально - проецирующая плоскость;

- профильно - проецирующая плоскость.

10. Точки схода следов плоскости – прописными буквами X, Y, Z с индексами соответствующей плоскости: X , Y , Z .

 

Рис. 2 Рис. 3

 

При наличии на чертеже оси проекций х положение точки А относительно плоскостей проекций π ₁ и π ₂ установлено и отрезок А′А_х выражает расстояние точки А от плоскости проекций π ₂, а отрезок А′′А_х – расстояние точки А от плоскости проекций π ₁.

Две проекции точки вполне определяют ее положение в пространстве относительно данной системы плоскостей проекций.

В системе π ₁, π ₂ пространство разделено на четыре четверти – I,II, III, IV (рис. 4). Например точка А (рис. 2…3) располагается в первой четверти.

Рис. 4

 

Таблица 1

Знаки координат в четвертях

Четверть	Знаки координат
x	y	z
I	+	+	+
II	+	-	+
III	+	-	-
IV	+	+	-

Конкурирующие точки

Точки, которые расположены на одном и том же проецирующем луче, т.е. одноименные проекции которых совпадают, называют конкурирующими.

а) горизонтально -конкурирующие точки (рис. 5);

Рассмотрим точки А и В, расположенные на одном проецирующем луче S₁ (S_1┴ π ₁). Горизонтальные проекции этих точек совпадают (А'≡В').

Рис. 5

 

Точка А закрывает собой точку В при проецировании на плоскость проекций π ₁, поэтому ее горизонтальная проекция будет видима, а у точки В – невидима.

 

б) фронтально – конкурирующие точки (рис. 6);

Рассмотрим точки С и D, расположенные на одном проецирующем луче S₂ (S_2┴ π ₂). Фронтальные проекции этих точек совпадают (C''≡D'').

Рис. 6

 

Точка D закрывает собой точку С по отношению к плоскости проекций π ₂,поэтому на фронтальной проекции точка С будет невидима, а точка D – видима.

Рис. 7

 

Можно утверждать, что такой чертеж (рис. 17) выражает отрезок прямой линии АВ, т.к. если представить себе, что через А′ В′ и через А′′ В′′ проведены проецирующие плоскости (т.е. перпендикулярные соответственно к π ₁ и к π ₂), то в пересечении этих плоскостей получается прямая и ее отрезок АВ (рис.8).

 

Рис. 8

 

Проекции прямой могут быть заданы положением относительно осей проекций.

Проекции заданных таким образом прямых обозначаются малыми латинскими буквами (рис. 9).

а ′′ - фронтальная проекция прямой а; а ′ - горизонтальная проекция прямой а.

Рис. 9

 

Положения прямой

Прямая линия относительно плоскостей проекций может занимать семь положений.

 

Горизонтальная прямая

Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной. На рисунках 10 изображен отрезок прямой АВ║ π ₁.

Рис. 10

 

Следует отметить:

а) горизонтальная проекция горизонтальной прямой равна длине самого отрезка (А′В′ = [AB]);

б) фронтальная проекция горизонтальной прямой параллельна оси проекций х. Если, например, А″В″ совпадает с осью проекций х, то это соответствует положению отрезка АВ в плоскости проекций π ₁;

в) угол, образованный горизонтальной проекцией прямой и осью х, равен углу наклона этой прямой к фронтальной плоскости проекций

 

(А′В′; х=[AB]; π ₂=<α^o).

 

Фронтальная прямая

Прямая, параллельная фронтальной плоскости проекций, называется фронтальной. На рисунках 11 изображен отрезок прямой CD║ π ₂.

Рис. 11

 

Для фронтальной прямой следует отметить:

а) фронтальная проекция этой прямой равна длине самого отрезка (С″D″=[CD]);

б) горизонтальная проекция фронтальной прямой параллельна оси х (С′D′║х); Если, например, С′D′ совпадает с осью проекций х, то это соответствует положению CD в пл. π ₂.

в) угол, образованный фронтальной проекцией прямой и осью х, равен углу наклона этой прямой к горизонтальной плоскости проекций

(С″D″; х = [CD]; π ₁ = <β^о).

 

Профильная прямая

Прямая, параллельная профильной плоскости проекций, называется профильной. На рисунках 12 изображен отрезок прямой EF║ π ₃.

Рис. 12

 

Для профильной прямой характерно:

а) профильная проекция этой прямой равна длине самого отрезка (E″′F″′=[EF]);

б) горизонтальная и фронтальная проекции профильной прямой располагаются на одном перпендикуляре к оси проекций х;

в) Е′′′F′′′; у = [EF]; π ₁= <α^о. Е′′′F′′′; z = [EF]; π ₂= <β^о

Прямые, параллельные одной плоскости проекций, т.е. горизонтальные, фронтальные и профильные называются прямыми уровня.

 

Рис. 13

 

У горизонтально - проецирующей прямой проекция на горизонтальную плоскость проекций представит собой точку. На фронтальную и профильную плоскости проекций она спроецируется в отрезки прямых, параллельных между собой и равных по длине самому отрезку (M″N″≡ M″′N″′=[MN]).

 

Рис.14

 

У фронтально-проецирующей прямой проекцией на фронтальную плоскость будет являться точка. На горизонтальную и профильную плоскости проекций она спроецируется в отрезки, равные по длине самому отрезку прямой (K′ L′ = K′′′ L′′′ = [KL]).

 

Рис. 15

 

У профильно-проецирующей прямой проекция на профильную плоскость проекций представит собой точку. На горизонтальную и фронтальную плоскости она спроецируется в отрезки прямых, параллельных между собой и равных по длине самому отрезку (G′F′=G′′F′′=[GF]).

Прямые, параллельные двум плоскостям проекций и перпендикулярные к третьей называются проецирующими.

Прямые уровня и проецирующие называют прямыми частного положения.

Прямая общего положения

Прямая, непараллельная ни к одной из плоскостей проекций, называется прямой общего положения. На рисунках 16 изображен отрезок прямой ВС – общего положения.

Рис. 16

 

У прямой общего положения ни одна из проекций не параллельна оси проекций и не перпендикулярна к ней. Каждая из проекций меньше самого отрезка, (В′С′<ВС, В′′С′′<ВС, В′′′С′′′<ВС.

Рис. 17

 

б) прямой линией и точкой взятой вне прямой (рис. 18);

 

 

Рис. 18

 

в) двумя пересекающимися прямыми (рис. 19);

 

Рис. 19

 

 

г) двумя параллельными прямыми (рис. 20);

Рис. 20

 

д) проекциями любой плоской фигуры - треугольника, квадрата, окружности (рис. 21), собственно это вариант способа задания плоскости пересекающимися прямыми, а задание плоскости треугольником вытекает из способа её задания тремя точками;

Рис. 21

 

 

е) плоскость может быть изображена на эпюре при помощи прямых, по которым она пересекает плоскости проекций, т.е. следами (рис. 22).

 

Рис. 22

 

Прямые, по которым некоторая плоскость пересекает плоскости проекций, называются следами этой плоскости на плоскостях проекций или короче следами плоскости.

На рисунке 22 изображена плоскость α пересекающая горизонтальную плоскость проекций по прямой, обозначаемой h_oα и фронтальную плоскость по прямой, обозначаемой ƒ_оα.

Прямая h_oα называется горизонтальным следом плоскости, прямая ƒ_оα – фронтальным следом плоскости α.

Точка пересечения плоскости α с осью проекций х (точка пересечения следов плоскости) называется точкой схода следов, обозначена х_α.

След плоскости на плоскости проекций сливается со своей проекцией на этой плоскости. Так горизонтальный след плоскости α сливается со своей горизонтальной проекцией (h′_оα≡h_oα), фронтальная проекция этого следа (h′′_оα) располагается на оси проекций х.

Фронтальный след плоскости α сливается со своей фронтальной проекцией (f′′_oα≡f_oα), горизонтальная проекция этого следа (f′_оα) располагается на оси проекций х.

На чертеже плоскость может быть задана следами (рис. 22). Такой чертеж нагляден и удобен для построений.

Угол, образованный между следами на чертеже не равен углу, образованному следами плоскости в пространстве.

 

Положения плоскости

Плоскость, как и прямая линия, относительно плоскостей проекций может занимать семь положений.

 

Плоскости общего положения.

Такие плоскости не перпендикулярны ни к одной из плоскостей проекций. Следы плоскостей общего положения никогда не перпендикулярны к осям проекций. На рисунке 22 дан пример плоскости общего положения.

 

2) Плоскости, перпендикулярные двум плоскостям проекций (возможны три случая):

а) горизонтальная плоскость (рис. 23);

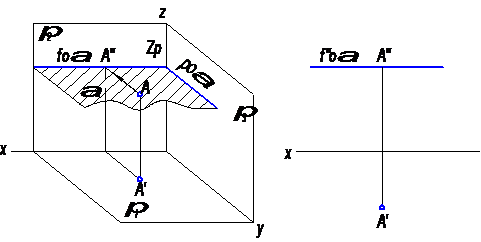
Рис.23

 

На рисунке 23 плоскость α║ π ₁, т.е. α _┴ π ₂ и π ₃.

Фронтальная проекция точки А, лежащей в плоскости α, будет расположена на фронтальном следе этой плоскости.

 

б) фронтальная плоскость (рис. 24);

Рис.24

 

На рисунке 24 плоскость β║ π ₂, т.е. β _┴ π ₁ и π ₃.

Горизонтальная проекция точки В, лежащей в плоскости β, будет расположена на горизонтальном следе плоскости

в) профильная плоскость (рис. 25);

Рис. 25

 

На рисунке 25 плоскость α║ π ₃, т.е. α _┴ π ₁ и π ₂.

Горизонтальная проекция точки С, лежащей в плоскости α, будет расположена на горизонтальном следе этой плоскости, фронтальная проекция точки С – на фронтальном следе плоскости α.

3) Плоскости, перпендикулярные одной плоскости проекций (возможны так же три случая):

а) горизонтально – проецирующая плоскость (рис. 26);

Рис.26

 

На рисунке 26 плоскость α _┴ π ₁. Фронтальный след перпендикулярен к плоскости π ₁ и к оси проекций х. Горизонтальный же след составляет с осью проекций не прямой угол, равный углу между горизонтально – проецирующей плоскостью и плоскостью проекций π ₂.

б) фронтально – проецирующая плоскость (рис. 27);

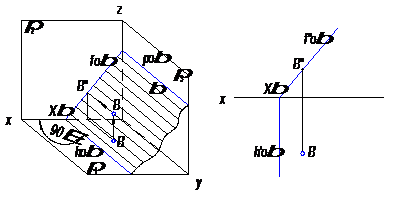
Рис. 27

 

На рисунке 27 плоскость β _┴ π ₂. Горизонтальный след перпендикулярен к плоскости π ₂ и к оси проекций х. Фронтальный след составляет с осью проекций не прямой угол, равный углу между фронтально – проецирующей плоскостью и плоскостью π ₁.

в) профильно – проецирующая плоскость (рис. 28);

Рис. 28

На рисунке 28 дана плоскость α _┴ π ₃.

Горизонтальный и фронтальный следы этой плоскости параллельны оси х и, следовательно, параллельны между собой. Угол γ^о – это угол, который образует профильно – проецирующая плоскость α с горизонтальной плоскостью проекций.

 

Главные линии плоскости

К числу прямых, занимающих особое положение в плоскости, относят горизонтали, фронтали, профильные прямые и линии наибольшего наклона к плоскостям проекций

Горизонталями плоскости называются прямые, лежащие в ней и параллельные горизонтальной плоскости проекций Горизонтали принято обозначать на чертежах буквой h (рис. 29).

Рис. 29

 

На рисунке 29 построены горизонтали плоскостей α и β (∆АВС).

Т. к. горизонталь плоскости есть прямая, параллельная плоскости π₁, то фронтальную проекцию h′′ строят параллельно оси х. Плоскость α на рисунке 29 задана следами и горизонтальный след этой плоскости есть ее нулевая горизонталь. Горизонтальная проекция горизонтали h′ параллельна горизонтальному следу плоскости h_оα.

Построенная прямая АК на рисунке 29 является горизонталью плоскости β (∆АВС); эта прямая лежит в плоскости, так как проходит через две точки ей принадлежащие и параллельна плоскости π₁.

Фронталями плоскости называются прямые, лежащие в ней и параллельные плоскости проекций π ₂.

Фронтали принято обозначать на чертежах буквой f (рис. 30).

Построение фронталей начинают с построения горизонтальной проекции – f ′.

 

Рис. 30

 

Т. к. фронталь плоскости есть прямая параллельная плоскости π ₂, то горизонтальную проекцию f ′ строят паралельно оси х. Фронтальный след плоскости α есть ее нулевая фронраль, поэтому фронтальная проекция фронтали – f ′′ (рис. 30) параллельна фронтальному следу плоскости – f_оα.

Построенная на рисунке 30 прямая AК является фронталью плоскости ∆АВС; эта прямая лежит в плоскости, т. к. проходит через точки А и К, принадлежащие ей, и параллельна плоскости π ₂.

 

Рис. 32 Рис. 33

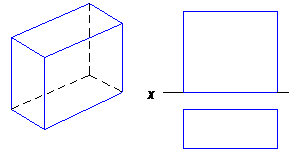
Рис. 34

 

Видимость ребер определяется по расположению конкурирующих точек, принадлежащих ребрам (рис. 35).

Чтобы определить видимость горизонтальной проекции ребра SA пирамиды SABC, нужно провести проецирующий луч S₁. Точка 1, принадлежащая ребру SA, расположена выше, чем точка 2, принадлежащая ребру SC. Отсюда ясно, что горизонтальная проекция точки 1 будет видимой, а горизонтальная проекция точки 2 – невидимой. Следовательно, и горизонтальная проекция ребра SA будет видимой.

Чтобы определить видимость фронтальной проекции ребра SC, проведем проецирующий луч S₂. Точка 3, расположенная на стороне АВ основания пирамиды SABC, находится к наблюдателю ближе, чем точка 4 на ребре SC. Отсюда ясно, что фронтальная проекция точки 3 будет видимой, а фронтальная проекция точки 4 – невидимой; Следовательно, фронтальная проекция ребра SC будет невидимой.

 

Рис. 35

 

 

Поверхности вращения

Поверхностью вращения общего вида называют поверхность, которая образуется произвольной прямой или кривой (плоской или пространственной) при ее вращении вокруг неподвижной оси.

Каждая точка образующей при вращении вокруг оси описывает окружность с центром на оси вращения. Эти окружности называют параллелями. Наибольшую параллель называют экватором.

Плоскости, проходящие через ось поверхности вращения, называют меридиональными, а линии, по которым они пересекают поверхность, – меридианами. Меридиональную плоскость, параллельную плоскости проекций π₂, принято называть главной меридиональной плоскостью, а линию пересечения с поверхностью вращения – главным меридианом.

При задании поверхности вращения на чертеже обычно указывают проекции ее оси, главного меридиана и экватора.

В технике, в частности в машиностроении, поверхности вращения находят широкое применение. Это объясняется распространенностью вращательного движения на станках.

Особенно распространены поверхности, имеющие в меридиональном сечении кривую второго порядка или две прямые, на которые распадается эта кривая.

Некоторые поверхности вращения представляют собой частные случаи поверхностей, в качестве образующей которых является окружность. В зависимости от взаимного расположения окружности (или ее дуги) и оси вращения можно получить различные поверхности:

1) тор (рис. 36 – 38);

тором называется поверхность, которая может быть получена при вращении окружности вокруг оси, не проходящей через ее центр.

В зависимости от соотношения величин R – радиуса образующей окружности и расстояния t от центра окружности до оси вращения поверхности тора подразделяют:

а) открытый тор (или кольцо) при R<t – окружность не пересекает ось вращения(рис.36);

Рис. 36

б) замкнутый тор, R = t(рис.37);

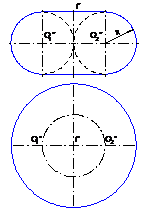
Рис.37

 

в) самопересекающийся тор, R>t(рис.38);

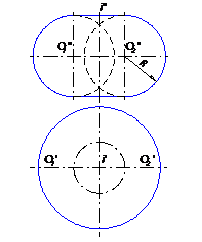
Рис.38

 

2)цилиндр вращения (рис.39);

Рис.39

 

 

3) конус вращения (рис.40);

Рис.40

 

Для цилиндра и конуса вращения меридианы являются прямыми линиями – в первом случае параллельными оси и равноудаленными от нее, во втором случае пересекающими ось в одной и той же точке, под одним и тем же углом к оси.

Меридиан цилиндра на рисунке 39 – прямоугольник, а конуса на рисунке 40 – треугольник.

 

4) сфера (рис.41);

Рис. 41

 

Сфера образуется в том случае, когда центр окружности принадлежит оси вращения. Сферу можно рассматривать как частный случай тора, у которого t=0.

5) гиперболоид вращения (рис. 42);

 

Для гиперболоида вращения меридианом является гипербола, причем если осью вращения служит действительная ось гиперболы, то образуется двуполостный гиперболоид вращения; если же вращать гиперболу вокруг её мнимой оси, то однополостный.

Однополостный гиперболоид вращения может быть образован также вращением прямой линии в случае, если образующая и ось вращения – скрещивающиеся прямые. На рисунке 42 показан однополостный гиперболоид вращения, образованный вращением прямой АВ вокруг указанной оси и ограниченный двумя параллелями. На однополостном гиперболоиде вращения можно нанести прямолинейные образующие в двух направлениях, например так, как показано на рисунке 42, и с наклоном в обратную сторону, под тем же углом к оси.

Кроме прямых (пар) на этой поверхности могут быть ещё гиперболы, параболы, эллипсы и окружности.

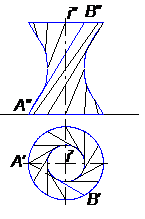
Рис. 42

 

Для параболоида вращения меридианом является парабола, ось которой служит осью поверхности.

Для эллипсоида вращения меридианом является эллипс. Поверхность может быть образована вращением эллипса вокруг его большой оси («вытянутый» эллипсоид вращения) или вокруг его малой оси («сжатый» эллипсоид вращения) (рис. 43).

а) «вытянутый» эллипсоид б) «сжатый» эллипсоид

Рис. 43

 

Контрольные вопросы

1. В чем заключается способ образования эпюра Монжа?

2. Что позволяют определять конкурирующие точки?

3. Назовите положение прямых.

4. Как можно задать плоскость на чертеже?

5. Что такое след плоскости?

6. Назовите положение плоскостей.

7. Какие главные линии плоскости вы знаете?

8. Какая поверхность называется многогранником? Какие гранные поверхности вы знаете.

9. Как определяется видимость ребер многогранника?

10. Как определяется не6достающая проекция точки принадлежащей многограннику?

11. Что называется поверхностью вращения? Какие поверхности вращения вы знаете?

12. Как определяется недостающая проекция точки принадлежащей поверхности вращения?

 

Рекомендуемая литература

1. Фролов, С.А. Начертательная геометрия: Учебник. 3-е изд., перераб. и доп. – М.: ИНФРА, 2010. – 285 с.

1. Чекмарев А.А. Начертательная геометрия и черчение: Учеб.для студ. высш. учеб. Заведений. – 2 – е изд., перераб. и доп. – М.: Гуманит. изд. центр ВЛАДОС, 2005. – 471 с.: ил.

3. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии. М.: Высш. шк., 2009. – 272 с.:ил.

4. Петлина Т.П. Начертательная геометрия. Ортогональные проекции и их преобразование: Учеб.пособие (с примерами практического использования в курсовом и дипломном проектировании). – Самара: СамВен, 2005. – 168 с.

Лекция 2

План лекции

1. Принадлежность точки – прямой, плоскости.

2. Принадлежность точки поверхности.

3. Пересечение прямой с плоскостью.

4. Пересечение плоскостей.

5. Пересечение прямой и плоскости с поверхностью.

 

Точка на прямой

Если известно, что точка принадлежит прямой (например, точка С принадлежит прямой АВ), то горизонтальная проекция точки находится на горизонтальной проекции данной прямой, фронтальная проекция этой точки находится на фронтальной проекции прямой (рис. 1).

Рис. 1

 

Следы прямой

Точка пересечения прямой с плоскостью проекций называется следом прямой.

Точка пересечения прямой с фронтальной плоскостью проекций называется фронтальным следом прямой.

Точка пересечения с горизонтальной плоскостью проекций называется горизонтальным следом прямой.

На рисунке 2 показаны точки Н и F, в которых прямая, заданная отрезком АВ пересекает плоскости проекций π ₁ и π ₂.

Горизонтальная проекция Н′ горизонтального следа Н совпадает с этим следом, а его фронтальная проекция Н′′ лежит на оси проекций х.

Фронтальная проекция F′′ фронтального следа F совпадает с этим следом, а его горизонтальная проекция F′ лежит на той же оси проекций – х.

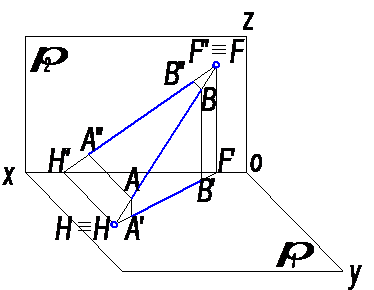
Рис. 2

 

Чтобы найти горизонтальный след прямой АВ, надо продолжить фронтальную проекцию А′′В′′ до пересечения с осью «х» и через найденную фронтальную проекцию Н′′ горизонтального следа Н, провести линию связи проекций Н′′ и Н′ до пересечения с продолжением горизонтальной проекции А′В′, что определит горизонтальную проекцию Н′ горизонтального следа Н, которая совпадает с самим следом (H′≡H), (рис. 3).

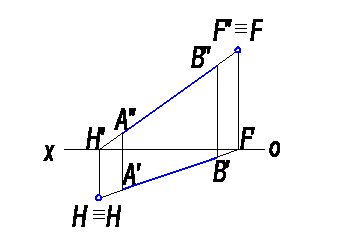
Рис. 3

 

Для нахождения фронтального следа продолжаем горизонтальную проекцию А′В′ до пересечения с осью х и найденную горизонтальную проекцию F′ фронтального следа F проводим линию связи проекций F′ и F′′ до пересечения с продолжением фронтальной проекции А′′В′′, что обозначит фронтальную проекцию F′′ фронтального следа F, которая совпадает с самим следом (F′′≡F).

Если плоскости проекций принять за плоскости координат, то у горизонтального следа прямой координата z = 0, у фронтального следа – у = 0.

По положению точек Н и F можно судить, к каким четвертям пространства отнесена данная прямая. На рисунке 3 прямая АВ проходит через, I, II, IV четверти.

Прямая не имеет следа на плоскости проекций в том случае, когда она параллельна этой плоскости.

 

Прямая в плоскости

Построение прямой линии в плоскости основано на двух положениях, известных из геометрии:

1) прямая принадлежит плоскости, если она проходит через две точки, принадлежащие данной плоскости.

2) прямая принадлежит плоскости, если она проходит через точку, принадлежащую данной плоскости и параллельна прямой, находящейся в этой плоскости или параллельной ей.

Допустим, что плоскость α определена двумя пересекающимися прямыми АВ и ВС, а плоскость β двумя параллельными прямыми DE и FG (рис. 4).

 

Рис.4

 

Согласно первому положению прямая, пересекающая прямые, определяющие плоскость, находится в данной плоскости.

Отсюда следует, что, если плоскость задана следами, то прямая принадлежит плоскости, если следы прямой находятся на одноименных следах плоскости (рис. 5).

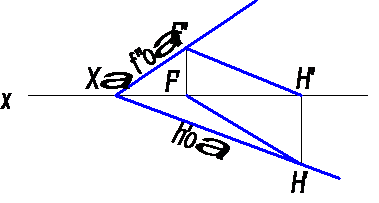
Рис.5

 

Из второго положения следует, что прямая принадлежит плоскости, если она параллельна одному из следов этой плоскости и имеет с другим следом общую точку (рис. 6).

Рис.6

Точка в плоскости

Чтобы построить на чертеже точку, лежащую в заданной плоскости, надо построить прямую, лежащую в этой плоскости и отметить на этой прямой точку.

Рассмотрим задачу. Известно, что точка М расположена в плоскости α (а∩в). Задана фронтальная проекция этой точки – М′′. Определить горизонтальную проекцию точки – М′(рис. 7).

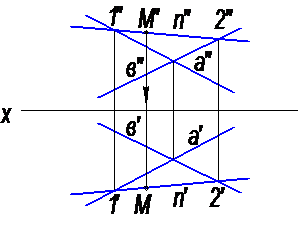
Рис. 7

Чтобы найти горизонтальную проекцию точки – М′, через ее фронтальную проекцию проведем фронтальную проекцию прямой – n′′ так, чтобы она пересекала фронтальные проекции прямых а ′′ и в ′′. По фронтальным проекциям точек пересечения – 1′′ и 2′′ определятся их горизонтальные проекции, затем через точки 1′ и 2′ строится горизонтальная проекция прямой – n′. Проведя из точки М′′ линию связи, получим горизонтальную проекцию точки – М′.

Точка М принадлежит плоскости α (а∩в), т. к. она расположена на прямой n, лежащей в этой плоскости.

 

Точка на многограннике

Если нужно на обеих проекциях многогранника построить точку, лежащую на одной из его граней, то следует «связать» точку с соответствующей гранью при помощи какой-либо прямой, находящейся на этой грани.

На рисунке 8 показано построение точки К на грани АSC пирамиды SABC.

Рис. 8

 

По данной горизонтальной проекции (К') точки К необходимо построить ее фронтальную проекцию. Для этого через горизонтальную проекцию вершины S пирамиды и точку К' проведена горизонтальная проекция прямой SM. Затем по горизонтальной проекции прямой SM построена её фронтальная проекция, на которой и определяется с помощью линии связи фронтальная проекция точки – К''.

Рис. 9

На рисунке 10 показано нахождение проекций точек на сфере. По данной проекции А′ точки А построена фронтальная проекция – А′′; по данной проекции В′′ найдена горизонтальная проекция В′ точки В, удовлетворяющей дополнительному условию, что точка В невидима при фронтальном проецировании.

Точка С задана на экваторе; её проекция С′ находится на очерке горизонтальной проекции сферы, т.е. на горизонтальной проекции экватора.

Точка К лежит на главном меридиане; она принадлежит параллели, на которой находится точка А.

Точка D также находится на главном меридиане, причем она невидима при горизонтальном проецировании.

Рис. 10

Рис. 11

 

На рисунке 11б задана следами горизонтально – проецирующая плоскость α и прямая m общего положения (аксонометрическое изображение на рис. 11а). Точка их пересечения К принадлежит и прямой m, и плоскости α. Следовательно, ее горизонтальная проекция К′ принадлежит и горизонтальному следу плоскости h_oα, т. к. α _┴ π ₁, и горизонтальной проекции прямой – m′. По горизонтальной проекции точки – К′ находим ее фронтальную проекцию – К′′ на фронтальной проекции прямой – m′′.

По горизонтальной проекции видно, что левее точки К, прямая m находится за плоскостью α, которая закрывает этот участок прямой на фронтальной проекции. Условно считают плоскость α не прозрачной, поэтому на чертеже фронтальная проекция прямой левее К′′ показана как невидимая, штриховой линией. На горизонтальной проекции вся прямая m видимая.

Здесь необходимо отметить собирательное свойство проецирующих плоскостей: все, что находится в горизонтально-проецирующей плоскости (точка, прямая, кривая…) спроецируется на горизонтальную плоскость проекций на горизонтальный след этой плоскости.

Все, что находится во фронтально-проецирующей плоскости спроецируется на фронтальную плоскость проекций на фронтальный след этой плоскости.

Все, что расположено в профильно-проецирующей плоскости спроецируется на профильную плоскость проекций на профильный след этой плоскости.

Рис. 12

 

Прямую MN заключили во вспомогательную горизонтально-проецирующую плоскость γ, которая задана только одним следом - h_оγ, проходящим через M′N′. Плоскость γ пересекает ∆ АВС по прямой DE. Линия пересечения DE и заданная прямая MN расположены в одной плоскости – γ и они пересекаются, что видно из их фронтальных проекций, в точке К, которая является общей для заданных прямой и треугольника. Т.е. будет определена фронтальная проекция К′′ точки пересечения К прямой MN с треугольником АВС. Горизонтальная проекция К′ определяется по ее фронтальной проекции с помощью линии связи.

Считая, что в пространстве ∆ АВС непрозрачный, необходимо определить видимые и невидимые части прямой MN относительно плоскости треугольника.

Видимость прямой MN в проекциях определена с помощью горизонтально- конкурирующих точек Е и Е₁ и фронтально-конкурирующих точек F и F₁. Границей видимости является точка К.

Из расположения фронтальных проекций E′′ и E₁′′ видно, что точка Е₁, принадлежащая прямой MN находится выше, чем точка Е, расположенная на стороне ВС ∆ АВС, а это значит, что горизонтальная проекция N′K будет видимой, а отрезок K′D′ будет невидимым (уйдет под треугольник).

Из распол