Аннотация: Рассматривается нахождение суммы элементов списка, среднего и минимального значений; алгоритмы сортировки списков: пузырьковый, выбором, вставкой, слиянием, быстрая сортировка.
В этой лекции речь пойдет о списках, элементами которых являются числа. Хотя в большинстве задач, которые будут рассматриваться, неважно, к какому домену относятся элементы списка, для определенности будем считать, что это целые числа.
Таким образом, списки, с которыми мы планируем работать, могут быть представлены в разделе описания доменов примерно следующим образом:
DOMAINS
listI = integer*
Для разминки решим несложный пример.
Пример. Создадим предикат, позволяющий вычислить сумму элементов списка.
Решение будет напоминать подсчет количества элементов списка. Отличаться они будут шагом рекурсии. При подсчете количества элементов нам было неважно, чему равен первый элемент списка, мы просто добавляли единицу к уже подсчитанному количеству элементов хвоста. При вычислении суммы нужно будет учесть значение головы списка.
Так как в пустом списке элементов нет, сумма элементов пустого списка равна нулю. Для вычисления суммы элементов непустого списка нужно к сумме элементов хвоста добавить первый элемент списка. Запишем эту идею:
sum([], 0). /* сумма элементов пустого списка равна
нулю */
sum([H|T], S):–
sum(T, S_T), /* S_T — суммаэлементовхвоста */
S = S_T + H. /* S — сумма элементов исходного
списка */
Попробуйте самостоятельно изменить этот предикат так, чтобы он вычислял не сумму элементов списка, а их произведение.
Еще один вариант данного предиката можно написать, используя накопитель. В нем будем хранить уже насчитанную сумму. Начинаем с пустым накопителем. Переходя от вычисления суммы непустого списка к вычислению суммы элементов его хвоста, будем добавлять первый элемент к уже насчитанной сумме. Когда элементы списка будут исчерпаны (список опустеет), передадим "накопленную" сумму в качестве результата в третий аргумент.
Запишем:
sum_list([],S,S). /* список стал пустым, значит
в накопителе — сумма элементов
списка */
sum_list([H|T],N,S):–
N_T=H+N,
/* N_T — результат добавления к сумме,
находящейся в накопителе, первого
элемента списка */
sum_list(T,N_T,S).
/* вызываем предикат от хвоста T и N_T */
Если нам нужно вызвать предикат от двух аргументов, а не от трех, то можно добавить вспомогательный предикат:
sum2(L,S):–
sum_list(L,0,S).
Последний вариант, в отличие от первого, реализует хвостовую рекурсию.
Разберем еще один простой пример.
Пример. Напишем предикат, вычисляющий среднее арифметическое элементов списка.
Конечно, можно, как всегда, опереться на рекурсию, но проще воспользоваться тем, что у нас уже есть предикаты, которые позволяют вычислить количество и сумму элементов списка. Для нахождения среднего нам достаточно будет сумму элементов списка разделить на их количество. Это можно записать следующим образом:
avg(L,A):–
summa(L,S), /* помещаем в переменную S сумму
элементов списка */
length(L,K), /* переменная K равна количеству
элементов списка */
A=S/K. /* вычисляем среднее как отношение суммы
к количеству */
Единственная проблема возникает при попытке найти среднее арифметическое элементов пустого списка. Если мы попытаемся вызвать цель avg([],A), то получим сообщение об ошибке " Division by zero" (" Деление на ноль"). Это произойдет, потому что предикат length([],K) конкретизирует переменную K нулем, а при попытке достижения третьей подцели A=S/K и произойдет вышеупомянутая ошибка. Можно посчитать это нормальной реакцией предиката. Раз в пустом списке нет элементов, значит, нет и их среднего арифметического. А можно изменить этот предикат так, чтобы он работал и с пустым списком.
Дабы обойти затруднение с пустым списком, добавим в нашу процедуру, в виде факта, информацию о том, что среднее арифметическое элементов пустого списка равно нулю. Полное решение будет выглядеть следующим образом.
avg([],0):–!.
avg(L,A):–
summa(L,S),
length(L,K),
A=S/K.
Описывая этот предикат в разделе описания предикатов PREDICATES, обратите внимание на то, что второй аргумент будет не целого типа, а вещественного (при делении одного целого числа на другое целое число частное может получиться нецелым).
Пример. Создадим предикат, находящий минимальный элемент списка.
Как обычно, наше решение будет рекурсивным. Но так как для пустого списка понятие минимального элемента не имеет смысла, базис рекурсии мы запишем не для пустого, а для одноэлементного списка. В одноэлементном списке, естественно, минимальным элементом будет тот самый единственный элемент списка ("при всем богатстве выбора другой альтернативы нет!").
Шаг рекурсии: найдем минимум из первого элемента списка и минимального элемента хвоста — это и будет минимальный элемент всего списка.
Оформим эти рассуждения:
min_list([X],X). /* единственный элемент одноэлементного
списка является минимальным элементом
списка */
min_list([H|T],M):–
min_list(T,M_T), /* M_T — минимальный элемент хвоста */
min(H,M_T,M). /* M — минимум из M_T и первого элемента
исходного списка */
Обратите внимание на то, что в правиле, позволяющем осуществить шаг рекурсии, использован предикат min, подобный предикатуmax, который был разобран нами в третьей лекции.
Слегка модифицировав предикат min_list (подставив в правило вместо предиката min предикат max и поменяв его название), получим предикат, находящий не минимальный, а максимальный элемент списка.
Перейдем теперь к более интересной задаче, а именно, к сортировке списков. Под сортировкой обычно понимают расстановку элементов в некотором порядке. Для определенности мы будем упорядочивать элементы списков по неубыванию. То есть, если сравнить любые два соседних элемента списка, то следующий должен быть не меньше предыдущего.
Существует множество алгоритмов сортировки. Заметим, что имеется два класса алгоритмов сортировки: сортировка данных, целиком расположенных в основной памяти (внутренняя сортировка), и сортировка файлов, хранящихся во внешней памяти (внешняя сортировка). Мы займемся исключительно методами внутренней сортировки.
Рассмотрим наиболее известные методы внутренней сортировки и выясним, как можно применить их для сортировки списков в Прологе.
Начнем с наиболее известного "пузырькового" способа сортировки. Его еще называют методом прямого обмена или методом простого обмена.
Пузырьковая сортировка
Идея этого метода заключается в следующем. На каждом шаге сравниваются два соседних элемента списка. Если оказывается, что они стоят неправильно, то есть предыдущий элемент больше следующего, то они меняются местами. Этот процесс продолжаем до тех пор, пока есть пары соседних элементов, расположенные в неправильном порядке. Это и будет означать, что список отсортирован.
Аналогия с пузырьком вызвана тем, что при каждом проходе минимальные элементы как бы "всплывают" к началу списка.
Реализуем пузырьковую сортировку посредством двух предикатов. Один из них, назовем его permutation, будет сравнивать два первых элемента списка и в случае, если первый окажется больше второго, менять их местами. Если же первая пара расположена в правильном порядке, этот предикат будет переходить к рассмотрению хвоста.
Основной предикат bubble будет осуществлять пузырьковую сортировку списка, используя вспомогательный предикат permutation.
permutation([X,Y|T],[Y,X|T]):–X>Y,!. /* переставляем первые два элемента, если первый больше второго */permutation([X|T],[X|T1]):–permutation(T,T1). /*переходим к перестановкам в хвосте*/bubble(L,L1):– permutation(L,LL), /* вызываем предикат,осуществляющий перестановку */!, bubble(LL,L1). /* пытаемся еще раз отсортировать полученный список */bubble(L,L). /* если перестановок не было, значит список отсортирован */
Но наш пузырьковый метод работает только до тех пор, пока есть хотя бы пара элементов списка, расположенных в неправильном порядке. Как только такие элементы закончились, предикат permutation терпит неудачу, а bubble переходит от правила к факту и возвращает в качестве второго аргумента отсортированный список.
Сортировка вставкой
Теперь рассмотрим сортировку вставкой. Она основана на том, что если хвост списка уже отсортирован, то достаточно поставить первый элемент списка на его место в хвосте, и весь список будет отсортирован. При реализации этой идеи создадим два предиката.
Задача предиката insert — вставить значение (голову исходного списка) в уже отсортированный список (хвост исходного списка), так чтобы он остался упорядоченным. Его первым аргументом будет вставляемое значение, вторым — отсортированный список, третьим — список, полученный вставкой первого аргумента в нужное место второго аргумента так, чтобы не нарушить порядок.
Предикат ins_sort, собственно, и будет организовывать сортировку исходного списка методом вставок. В качестве первого аргумента ему дают произвольный список, который нужно отсортировать. Вторым аргументом он возвращает список, состоящий из элементов исходного списка, стоящих в правильном порядке.
ins_sort([ ],[ ]). /* отсортированный пустой список остается пустым списком */ins_sort([H|T],L):– ins_sort(T,T_Sort),/* T — хвост исходного списка, T_Sort — отсортированный хвост исходного списка */ insert(H,T_Sort,L)./* вставляем H (первый элемент исходного списка)в T_Sort,получаем L (список, состоящий из элементов исходного списка, стоящих по неубыванию) */insert(X,[],[X]). /* при вставке любого значения в пустой список, получаем одноэлементный список */insert(X,[H|T],[H|T1]):– X>H,!, /* если вставляемое значение больше головы списка, значит его нужно вставлять в хвост */ insert(X,T,T1). /* вставляем X в хвост T, в результате получаем список T1 */insert(X,T,[X|T]). /* это предложение (за счет отсечения в предыдущем правиле) выполняется, только если вставляемое значение не больше головы списка T, значит, добавляем его первым элементом в список T */
Сортировка выбором
Идея алгоритма сортировки выбором очень проста. В списке находим минимальный элемент (используя предикат min_list, который мы придумали в начале этой лекции). Удаляем его из списка (с помощью предиката delete_one, рассмотренного в предыдущей лекции). Оставшийся список сортируем. Приписываем минимальный элемент в качестве головы к отсортированному списку. Так как этот элемент был меньше всех элементов исходного списка, он будет меньше всех элементов отсортированного списка. И, следовательно, если его поместить в голову отсортированного списка, то порядок не нарушится.
Запишем:
choice([ ],[ ]). /* отсортированный пустой список остается пустым списком */choice(L,[X|T]):– /* приписываем X (минимальный элемент списка L) к отсортированному списку T */ min_list(L,X), /* X — минимальный элемент списка L */ delete_one(X,L,L1),/* L1 — результат удаления первого вхождения элемента X из списка L */ choice(L1,T). /* сортируем список L1, результат обозначаем T */
Быстрая сортировка
Автором так называемой "быстрой" сортировки является Хоар. Он назвал ее быстрой потому, что в общем случае эффективность этого алгоритма довольно высока. Идея метода следующая. Выбирается некоторый "барьерный" элемент, относительно которого мы разбиваем исходный список на два подсписка. В один мы помещаем элементы, меньшие барьерного элемента, во второй — большие либо равные. Каждый из этих списков мы сортируем тем же способом, после чего приписываем к списку тех элементов, которые меньше барьерного, вначале сам барьерный элемент, а затем — список элементов не меньших барьерного. В итоге получаем список, состоящий из элементов, стоящих в правильном порядке.
При воплощении в программный код этой идеи нам, как обычно, понадобится пара предикатов.
Вспомогательный предикат partition будет отвечать за разбиение списка на два подсписка. У него будет четыре аргумента. Первые два элемента — входные: первый — исходный список, второй — барьерный элемент. Третий и четвертый элементы — выходные, соответственно, список элементов исходного списка, которые меньше барьерного, и список, состоящий из элементов, которые не меньше барьерного элемента.
Предикат quick_sort будет реализовывать алгоритм быстрой сортировки Хоара. Он будет состоять из двух предложений. Правило будет осуществлять с помощью предиката partition разделение непустого списка на два подсписка, затем сортировать каждый из этих подсписков рекурсивным вызовом себя самого, после чего, используя предикат conc (созданный нами ранее), конкретизирует второй аргумент списком, получаемым объединением отсортированного первого подсписка и списка, сконструированного из барьерного элемента (головы исходного списка) и отсортированного второго подсписка. Запишем это:
quick_sort([],[]). /* отсортированный пустой список остается пустым списком */quick_sort([H|T],O):–partition(T,H,L,G),/* делим список T на L (список элементов меньших барьерного элемента H) и G (список элементов не меньших H) */ quick_sort(L,L_s), /* список L_s — результат упорядочивания элементов списка L */ quick_sort(G,G_s),/* аналогично, список G_s — результат упорядочивания элементов списка G */ conc(L_s,[H|G_s],O). /* соединяем список L_s со списком, у которого голова H, а хвост G_s, результат обозначаем O */partition([],_,[],[]). /* как бы мы ни делили элементы пустого списка, ничего кроме пустых списков не получим */partition([X|T],Y,[X|T1],Bs):– X<Y,!,partition(T,Y,T1,Bs)./* если элемент X меньше барьерного элемента Y, то мы добавляем его в третий аргумент */partition([X|T],Y,T1,[X|Bs]):–partition(T,Y,T1,Bs)./* в противном случае дописываем его в четвертый аргумент */
Прежде чем перейти к изучению следующего алгоритма сортировки, решим одну вспомогательную задачу.
Пусть у нас есть два упорядоченных списка, и мы хотим объединить их элементы в один список так, чтобы объединенный список также остался отсортированным.
Идея реализации предиката, осуществляющего слияние двух отсортированных списков с сохранением порядка, довольно проста. Будем на каждом шаге сравнивать головы наших упорядоченных списков и ту из них, которая меньше, будем переписывать в результирующий список. И так до тех пор, пока один из списков не закончится. Когда один из списков опустеет, нам останется дописать остатки непустого списка к уже построенному итогу. В результате получим список, состоящий из элементов двух исходных списков, причем элементы его расположены в нужном нам порядке.
Создадим предикат (назовем его fusion), реализующий приведенное описание. Так как мы не знаем, какой из списков опустеет раньше, нам необходимо "гнать" рекурсию сразу по обоим базовым спискам. У нас будет два факта — основания рекурсии, которые будут утверждать, что если мы сливаем некий список с пустым списком, то в итоге получим, естественно, тот же самый список. Причем этот факт имеет место и в случае, когда первый список пуст, и в случае, когда пуст второй список.
Шаг рекурсии нам дадут два правила: первое будет утверждать, что если голова первого списка меньше головы второго списка, то именно голову первого списка и нужно дописать в качестве головы в результирующий список, после чего перейти к слиянию хвоста первого списка со вторым. Результат этого слияния будет хвостом итогового списка. Второе правило, напротив, будет дописывать голову второго списка в качестве головы результирующего списка, сливать первый список с хвостом второго списка. Итог этого слияния будет хвостом объединенного списка.
fusion(L1,[ ],L1):–!. /* при слиянии списка L1 с пустым списком получаем список L1 */fusion([ ],L2,L2):–!. /* при слиянии пустого списка со списком L2 получаем список L2 */fusion([H1|T1],[H2|T2],[H1|T]):–H1<H2,!, /* если голова первого списка H1 меньше головы второго списка H2 */fusion(T1, [H2|T2],T)./* сливаем хвост первого списка T1 со вторым списком [H2|T2] */fusion(L1, [H2|T2],[H2|T]):–fusion(L1,T2,T). /* сливаем первый список L1 с хвостом второго списка T2 */
Теперь можно перейти к изучению алгоритма сортировки слияниями.
Сортировка слияниями
Метод слияний — один из самых "древних" алгоритмов сортировки. Его придумал Джон фон Нейман еще в 1945 году. Идея этого метода заключается в следующем. Разобьем список, который нужно упорядочить, на два подсписка. Упорядочим каждый из них этим же методом, после чего сольем упорядоченные подсписки обратно в один общий список.
Для начала создадим предикат, который будет делить исходный список на два. Он будет состоять из двух фактов и правила. Первый факт будет утверждать, что пустой список можно разбить только на два пустых подсписка. Второй факт будет предлагать разбиение одноэлементного списка на тот же одноэлементный список и пустой список. Правило будет работать в случаях, не охваченных фактами, т.е. когда упорядочиваемый список содержит не менее двух элементов. В этой ситуации мы будем отправлять первый элемент списка в первый подсписок, второй элемент — во второй подсписок, и продолжать распределять элементы хвоста исходного списка.
splitting([],[],[])./* пустой список можно расщепить только на пустые подсписки */splitting([H],[H],[]). /* одноэлементный список разбиваем на одноэлементный список и пустой список */splitting([H1,H2|T],[H1|T1],[H2|T2]):–splitting(T,T1,T2). /* элемент H1 отправляем в первый подсписок, элемент H2 — во второй подсписок, хвост T разбиваем на подсписки T1 и T2 */
Теперь можно приступать к записи основного предиката, который, собственно, и будет осуществлять сортировку списка. Он будет состоять из трех предложений. Первое будет декларировать очевидный факт, что при сортировке пустого списка получается пустой список. Второе утверждает, что одноэлементный список также уже является упорядоченным. В третьем правиле будет содержаться суть метода сортировки слиянием. Вначале список расщепляется на два подсписка с помощью предиката splitting, затем каждый из них сортируется рекурсивным вызовом предиката fusion_sort, и, наконец, используя предикат fusion, сливаем полученные упорядоченные подсписки в один список, который и будет результатом упорядочивания элементов исходного списка.
Запишем изложенные выше соображения.
fusion_sort([],[]):–!./* отсортированный пустой список остается пустым списком */fusion_sort([H],[H]):–!. /* одноэлементный список упорядочен */fusion_sort(L,L_s):–splitting(L,L1,L2), /* расщепляем список L на два подсписка */ fusion_sort(L1,L1_s),/* L1_s — результат сортировки L1 */fusion_sort(L2,L2_s),/* L2_s — результат сортировки L2 */fusion(L1_s,L2_s,L_s)./* сливаем L1_s и L2_s в список L_s */
Фактически этот алгоритм при прямом проходе дробит список на одноэлементные подсписки, после чего на обратном ходе рекурсии сливает их двухэлементные списки. На следующем этапе сливаются двухэлементные списки и т.д. На последнем шаге два подсписка сливаются в итоговый, отсортированный список.
В качестве завершения темы сортировки разработаем предикат, который будет проверять, является ли список упорядоченным. Это совсем не сложно. Для того чтобы список был упорядоченным, он должен быть либо пустым, либо одноэлементным, либо любые два его соседних элемента должны быть расположены в правильном порядке. Запишем эти рассуждения.
sorted([ ]). /* пустой список отсортирован */sorted([_])./* одноэлементный список упорядочен */sorted([X,Y|T]):– X<=Y,sorted([Y|T]). /* список упорядочен, если первые два элемента расположены в правильном порядке и список,образованный вторым элементом и хвостом исходного, упорядочен */
Лекция 9: Множества
Аннотация: Реализация множеств в Прологе. Операции над множествами: превращение списка во множество, принадлежность элемента множеству, объединение, пересечение, разность, включение, дополнение.
В данной лекции мы попробуем реализовать некоторое приближение математического понятия "множество" в Прологе. Заметим, что в Прологе, в отличие от некоторых императивных языков программирования, нет такой встроенной структуры данных, как множество. И, значит, нам придется реализовывать это понятие, опираясь на имеющиеся стандартные домены. В качестве базового домена используем стандартный списковый домен, с которым мы работали на протяжении двух последних лекций.
Итак, что мы будем понимать под множеством? Просто список, который не содержит повторных вхождений элементов. Другими словами, в нашем множестве любое значение не может встречаться более одного раза.
На самом деле я не знаю ни одной реализации понятия множества, которая бы достаточно точно соответствовала этому математическому объекту. Наше подобие множества также, по большому счету, лишь отчасти будет приближаться к "настоящему" множеству.
Нам предстоит разработать предикаты, которые реализуют основные теоретико-множественные операции.
Начнем с написания предиката, превращающего произвольный список во множество, в том смысле, в котором мы договорились понимать этот термин. Для этого нужно удалить все повторные вхождения элементов. При этом мы воспользуемся предикатомdelete_all, который был создан нами ранее, в седьмой лекции. Предикат будет иметь два аргумента: первый — исходный список (возможно, содержащий повторные вхождения элементов), второй — выходной (то, что остается от первого аргумента после удаления повторных вхождений элементов).
Предикат будет реализован посредством рекурсии. Базисом рекурсии является очевидный факт: в пустом списке никакой элемент не встречается более одного раза. По правде говоря, в пустом списке нет ни одного элемента, который встречался бы в нем хотя бы один раз, то есть в нем вообще нет элементов. Шаг рекурсии позволит выполнить правило: чтобы сделать из непустого списка множество (в нашем понимании этого понятия), нужно удалить из хвоста списка все вхождения первого элемента списка, если таковые вдруг обнаружатся. После выполнения этой операции первый элемент гарантированно будет встречаться в списке ровно один раз. Для того чтобы превратить во множество весь список, остается превратить во множество хвост исходного списка. Для этого нужно только рекурсивно применить к хвосту исходного списка наш предикат, удаляющий повторные вхождения элементов. Полученный в результате из хвоста список с приписанным в качестве головы первым элементом и будет требуемым результатом (множеством, т.е. списком, образованным элементами исходного списка и не содержащим повторных вхождений элементов).
Закодируем наши рассуждения.
list_set([],[]). /* пустой список является множеством
в нашем понимании */
list_set ([H|T],[H|T1]):–
delete_all(H,T,T2),
/* T2 — результат удаления
вхождений первого элемента
исходного списка H из хвоста T */
list_set (T2,T1).
/* T1 — результат удаления
повторных вхождений элементов
из списка T2 */
Например, если применить этот предикат к списку [1,2,1,2,3, 2,1], то результатом будет список [1,2,3].
Заметим, что в предикате, обратном только что записанному предикату list_set и переводящем множество в список, нет никакой необходимости по той причине, что наше множество уже является списком.
Теперь займемся реализацией теоретико-множественных операций, таких как принадлежность элемента множеству, объединение, пересечение, разность множеств и т.д.
При реализации этих предикатов можно было бы воспользоваться предикатами, предназначенными для работы с обыкновенными списками, но в результате их применения могут получаться списки, содержащие некоторые элементы несколько раз, даже если исходные списки были множествами, в нашем понимании этого слова.
Можно, конечно, после каждого применения теоретико-множественной операции превращать полученный список обратно во множество применением вышеописанного предиката list_set, но это было бы не очень удобно. Вместо этого мы попробуем написать каждую из теоретико-множественных операций так, чтобы в результате ее работы гарантированно получалось множество.
Итак, приступим.
В качестве реализации операции принадлежности элемента множеству вполне можно использовать предикат member3, который мы разработали в седьмой лекции, когда только начинали знакомиться со списками. Напомним, что факт принадлежности элемента x множеству A в математике принято обозначать следующим образом:  .
.
Для того чтобы найти мощность множества, вполне подойдет предикат length, рассмотренный нами в седьмой лекции. Напомним, чтодля конечного множества мощность — это количество элементов во множестве.
Пример. Реализуем операцию объединения двух множеств. На всякий случай напомним, что под объединением двух множеств понимают множество, элементы которого принадлежат или первому, или второму множеству. Обозначается объединение множеств A иB через  . В математической записи это выглядит следующим образом:
. В математической записи это выглядит следующим образом:  . На рисунке объединение множеств A и B обозначено штриховкой.
. На рисунке объединение множеств A и B обозначено штриховкой.

Рис. 9.1. Объединение множеств A и B
У соответствующего этой операции предиката должно быть три параметра: первые два — множества, которые нужно объединить, третий параметр — результат объединения двух первых аргументов. В третий аргумент должны попасть все элементы, которые входили в первое или второе множество. При этом нам нужно проследить, чтобы ни одно значение не входило в итоговое множество несколько раз. Такое могло бы произойти, если бы мы попытались, например, воспользоваться предикатом conc (который мы рассмотрели в седьмой лекции), предназначенным для объединения списков. Если бы какое-то значение встречалось и в первом, и во втором списках, то в результирующий список оно бы попало, по крайней мере, в двойном количестве. Значит, вместо использования предиката concнужно написать новый предикат, применение которого не приведет к ситуации, в которой итоговый список уже не будет множеством за счет того, что некоторые значения будут встречаться в нем более одного раза.
Без рекурсии мы не обойдемся и здесь. Будем вести рекурсию по первому из объединяемых множеств. Базис индукции: объединяем пустое множество с некоторым множеством. Результатом объединения будет второе множество. Шаг рекурсии будет реализован посредством двух правил. Правил получается два, потому что возможны две ситуации: первая — голова первого множества является элементом второго множества, вторая — первый элемент первого множества не входит во второе множество. В первом случае мы не будем добавлять голову первого множества в результирующее множество, она попадет туда из второго множества. Во втором случае ничто не мешает нам добавить первый элемент первого списка. Так как этого значения во втором множестве нет, и в хвосте первого множества оно также не может встречаться (иначе это было бы не множество), то и в результирующем множестве оно также будет встречаться только один раз.
Давайте запишем эти рассуждения:
union([ ],S2,S2). /* результатом объединения
пустого множества со множеством S2
будет множество S2 */
union([H|T],S2,S):–
member3(H,S2),
/* если голова первого
множества H принадлежит второму
множеству S2, */
!,
union(T,S2,S).
/* то результатом S будет
объединение хвоста первого
множества T и второго
множества S2 */
union([H |T],S2,[H|S]):–
union(T,S2,S).
/* в противном случае результатом
будет множество, образованное
головой первого множества H
и хвостом, полученным объединением
хвоста первого множества T
и второго множества S2 */
Если объединить множество [1,2,3,4] со множеством [3,4,5], то в результате получится множество [1,2,3,4,5].
Пример. Теперь можно приступить к реализации операции пересечения двух множеств. Напомним, что пересечение двух множеств — это множество, образованное элементами, которые одновременно принадлежат и первому, и второму множествам. Обозначается пересечение множеств A и B через  . В математических обозначениях это выглядит следующим образом:
. В математических обозначениях это выглядит следующим образом:  . На рисунке пересечение множеств A и B обозначено штриховкой.
. На рисунке пересечение множеств A и B обозначено штриховкой.

Рис. 9.2. Пересечение множеств A и B
У предиката, реализующего эту операцию, как и у предиката, осуществляющего объединение двух множеств, есть три параметра: первые два — исходные множества, третий — результат пересечения двух первых аргументов. В итоговом множестве должны оказаться те элементы, которые входят и в первое, и во второе множество одновременно.
Этот предикат, наверное, будет немного проще объединения. Его мы также проведем рекурсией по первому множеству. Базис рекурсии: пересечение пустого множества с любым множеством будет пустым множеством. Шаг рекурсии так же, как и в случае объединения, разбивается на два случая в зависимости от того, принадлежит ли первый элемент первого множества второму. В ситуации, когда голова первого множества является элементом второго множества, пересечение множеств получается приписыванием головы первого множества к пересечению хвоста первого множества со вторым множеством. В случае, когда первый элемент первого множества не встречается во втором множестве, результирующее множество получается пересечением хвоста первого множества со вторым множеством.
Запишем это.
intersection([],_,[]). /* в результате пересечения
пустого множества с любым
множеством получается пустое
множество */
intersection([H|T1],S2,[H|T]):–
member3(H,S2),
/* если голова первого множества H
принадлежит второму множеству S2 */
!,
intersection(T1,S2,T).
/* то результатом будет множество,
образованное головой первого
множества H и хвостом, полученным
пресечением хвоста первого
множества T1 со вторым
множеством S2 */
intersection([_|T],S2,S):–
intersection(T,S2,S).
/* в противном случае результатом
будет множество S, полученное
объединением хвоста первого
множества T со вторым
множеством S2 */
Если пересечь множество [1,2,3,4] со множеством [3,4,5], то в результате получится множество [3,4].
Пример. Следующая операция, которую стоит реализовать, — это разность двух множеств. Напомним, что разность двух множеств — это множество, образованное элементами первого множества, не принадлежащими второму множеству. Обозначается разностьмножеств A и B через A–B или A\B. В математических обозначениях это выглядит следующим образом: 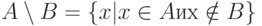 .
.
На рисунках разность множеств A и B (B и A) обозначена штриховкой.

Рис. 9.3. Разность множеств A и B

Рис. 9.4. Разность множеств В и А
В этой операции, в отличие от двух предыдущих, важен порядок множеств. Если в объединении или пересечении множеств поменять первый и второй аргументы местами, результат останется прежним. В то время как при A={1,2,3,4}, B={3,4,5}, A\B={1,2}, ноB\A={5}.
У предиката, реализующего разность, как и у объединения и пересечения, будет три аргумента: первый — множество, из которого нужно вычесть, второй — множество, которое нужно отнять, третий — результат вычитания из первого аргумента второго. В третий параметр должны попасть те элементы первого множества, которые не принадлежат второму множеству.
Рекурсия по первому множеству поможет нам реализовать вычитание. В качестве базиса рекурсии возьмем очевидный факт: при вычитании произвольного множества из пустого множества ничего кроме пустого множества получиться не может, так как в пустом множестве элементов нет. Шаг рекурсии, как и в случае объединения и пересечения, зависит от того, принадлежит ли первый элемент множества, из которого вычитают, множеству, которое вычитают. В случае, когда голова первого множества является элементом второго множества, разность множеств получается путем вычитания второго множества из хвоста первого. Когда первый элемент множества, из которого производится вычитание, не встречается в вычитаемом множестве, ответом будет множество, образованное приписыванием головы первого множества к результату вычитания второго множества из хвоста первого множества.
Запишем эти рассуждения.
minus([],_,[]). /* при вычитании любого множества
из пустого множества получится пустое
множество */
minus([H|T],S2,S):–
member3(H,S2),
/* если первый элемент первого
множества H принадлежит второму
множеству S2*/
!,
minus(T,S2,S).
/* то результатом S будет разность
хвоста первого множества T
и второго множества S2 */
minus([H|T],S2,[H|S]):–
minus(T,S2,S).
/* в противном случае, результатом
будет множество, образованное
первым элементом первого
множества H и хвостом, полученным
вычитанием из хвоста первого
множества T второго множества S2 */
Можно попробовать реализовать пересечение через разность. Из математики нам известно тождество  . Попробуем проверить это тождество, записав соответствующий предикат, реализующий пересечение множеств, через взятие разности.
. Попробуем проверить это тождество, записав соответствующий предикат, реализующий пересечение множеств, через взятие разности.
intersection2(A,B,S):–
minus(A,B,A_B), /*A_B=A\B */
minus(A,A_B,S). /* S = A\A_B = A\(A\B) */
Проверка на примерах показывает, что этот предикат, так же, как, впрочем, и ранее созданный предикат intersection, возвращает именно те результаты, которые ожидаются.
Пример. Не помешает иметь предикат, позволяющий проверить, является ли одно множество подмножеством другого. В каком случае одно множество содержится в другом? В случае, если каждый элемент первого множества принадлежит второму множеству. Тот факт, что множество A является подмножеством множества B, обозначается через  . В математической записи это выглядит следующим образом:
. В математической записи это выглядит следующим образом:  .
.
Предикат, реализующий данное отношение, будет иметь два параметра, оба входные. В качестве первого параметра будем указывать множество, включение которого мы хотим проверить. То множество, включение в которое первого аргумента нужно проверить, указывается в качестве второго параметра.
Решение, как обычно, будет рекурсивным. Базис рекурсии будет представлен фактом, утверждающим, что пустое множество является подмножеством любого множества. Шаг рекурсии: чтобы одно множество было подмножеством другого, нужно, чтобы его первый элемент принадлежал второму множеству (проверить это нам позволит предикат
member3, рассмотренный нами ранее в седьмой лекции), а его хвост, в свою очередь, должен быть подмножеством второго множества. Этих рассуждений достаточно, чтобы записать предикат, реализующий операцию включения.
subset([],_). /* пустое множество является
подмножеством любого множества */
subset([H|T],S):– /* множество [H|T] является
подмножеством множества S */
member3(H,S), /* если его первый элемент H
принадлежит S */
subset(T,S). /* и его хвост T является
подмножеством множества S */
Можно также определить это отношение, воспользовавшись уже определенными предикатами union и intersection.
Из математики известно, что  . То есть одно множество является подмножеством другого тогда и только тогда, когда их объединение с
. То есть одно множество является подмножеством другого тогда и только тогда, когда их объединение с



 .
. . В математической записи это выглядит следующим образом:
. В математической записи это выглядит следующим образом:  . На рисунке объединение множеств A и B обозначено штриховкой.
. На рисунке объединение множеств A и B обозначено штриховкой.
 . В математических обозначениях это выглядит следующим образом:
. В математических обозначениях это выглядит следующим образом:  . На рисунке пересечение множеств A и B обозначено штриховкой.
. На рисунке пересечение множеств A и B обозначено штриховкой.
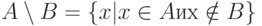 .
.

 . Попробуем проверить это тождество, записав соответствующий предикат, реализующий пересечение множеств, через взятие разности.
. Попробуем проверить это тождество, записав соответствующий предикат, реализующий пересечение множеств, через взятие разности. . В математической записи это выглядит следующим образом:
. В математической записи это выглядит следующим образом:  .
. . То есть одно множество является подмножеством другого тогда и только тогда, когда их объединение с
. То есть одно множество является подмножеством другого тогда и только тогда, когда их объединение с


