

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Интересное:
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Теорема 4. Пусть  , функции
, функции  и
и  интегрируемы на промежутке
интегрируемы на промежутке  и при всех
и при всех  справедливо неравенство
справедливо неравенство
 . (11)
. (11)
Тогда
 (12)
(12)
Доказательство. Рассмотрим разность интересующих нас интегралов как интеграл разности данных функций. В силу (9)

Последний интеграл запишем по формуле (4), т.е. следуя определению определённого интеграла. Тогда получим
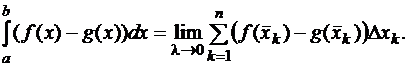
Здесь все парные произведения интегральной суммы неотрицательны. Действительно, по условию (11)  при всех
при всех 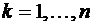 , а
, а  при всех
при всех 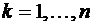 , поскольку
, поскольку  .
.
Значит и сама интегральная сумма неотрицательна. Тогда по теореме о предельном переходе в неравенстве неотрицателен и ее предел. Таким образом, получаем:

Теорема доказана.
Следствие. Пусть  , функция
, функция  интегрируема на промежутке
интегрируема на промежутке  и при всех
и при всех  справедливо неравенство
справедливо неравенство  . Тогда
. Тогда  .
.
Теорема 5. Если функция  интегрируема на промежутке
интегрируема на промежутке  , то функция
, то функция  также интегрируема на промежутке
также интегрируема на промежутке  и при
и при  справедливо неравенство
справедливо неравенство
 (13)
(13)
Доказательство. Проведем его только для непрерывных функций. Заметим, что
 (14)
(14)
для всех  . К цепочке неравенств (14) применим теорему 4. Получим
. К цепочке неравенств (14) применим теорему 4. Получим
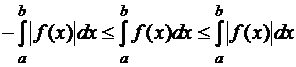 ,
,
Что равносильно неравенству (13).
Теорема о среднем значении
Теорема 6. Пусть функции  и
и  непрерывны на промежутке
непрерывны на промежутке  и пусть функция
и пусть функция  не меняет знака на этом промежутке. Тогда найдется такая точка
не меняет знака на этом промежутке. Тогда найдется такая точка  , что справедливо равенство
, что справедливо равенство
 (15)
(15)
Доказательство. Без ограничения общности будем считать, что  , а
, а  при
при  . Рассмотрим два случая.
. Рассмотрим два случая.
1). Пусть 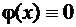 при всех
при всех  . Тогда равенство (15) выполнено очевидным образом.
. Тогда равенство (15) выполнено очевидным образом.
2). Пусть  не является тождественно равной нулю. Тогда в силу непрерывности функции
не является тождественно равной нулю. Тогда в силу непрерывности функции  можем утверждать, что
можем утверждать, что

Поскольку функция  непрерывна на замкнутом промежутке
непрерывна на замкнутом промежутке  , то она достигает на этом промежутке своего наибольшего значения
, то она достигает на этом промежутке своего наибольшего значения  и своего наименьшего значения
и своего наименьшего значения  , т.е. при всех
, т.е. при всех  справедливы неравенства
справедливы неравенства
|
|
 . (16)
. (16)
Домножим неравенства (16) на положительные значения функции  и получим справедливые при всех
и получим справедливые при всех  неравенства
неравенства
 (17)
(17)
К цепочке неравенств (17) применим теорему 4 и получим справедливые неравенства
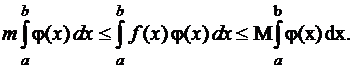 (18)
(18)
Разделим все части цепочки неравенств (18) на положительное число  . Получим
. Получим

Поскольку непрерывная функция  принимает на промежутке
принимает на промежутке  все значения между своим наибольшим
все значения между своим наибольшим  и наименьшим
и наименьшим  , существует такая точка
, существует такая точка  , что
, что

Отсюда следует, что

Таким образом, теорема 6 доказана.
Следствие. Если функция  непрерывна на промежутке
непрерывна на промежутке  , то можно указать такое значение
, то можно указать такое значение  , что
, что
 (19)
(19)
Доказательство. Будем считать 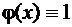 при
при  . Тогда согласно теореме 6 найдется такая точка
. Тогда согласно теореме 6 найдется такая точка  , что
, что

В случае, когда  при всех
при всех  , формула (19) имеет простой геометрический смысл. Рассмотрим криволинейную трапецию, ограниченную линиями
, формула (19) имеет простой геометрический смысл. Рассмотрим криволинейную трапецию, ограниченную линиями  . Согласно равенству(19) площадь этой криволинейной трапеции равна площади прямоугольника с основанием
. Согласно равенству(19) площадь этой криволинейной трапеции равна площади прямоугольника с основанием  и высотой
и высотой  (рис. 4).
(рис. 4).

Теорема Барроу
Рассмотрим определенный интеграл с переменным верхним пределом
 (20)
(20)
Здесь 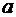 – число,
– число,  – переменная. Таким образом,
– переменная. Таким образом,  является функцией верхнего предела
является функцией верхнего предела  .
.
В силу геометрического смысла определённого интеграла, если  ,
,  , то величина
, то величина  является площадью криволинейной трапеции, ограниченной справа прямой
является площадью криволинейной трапеции, ограниченной справа прямой 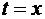 . Т.к.
. Т.к.  – переменная, то и интеграл (20) изображает трапецию с переменной площадью (рис. 5).
– переменная, то и интеграл (20) изображает трапецию с переменной площадью (рис. 5).

Справедливо следующее важное утверждение.
Теорема Барроу. Если функция  непрерывна, то
непрерывна, то
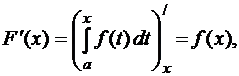
т.е. производная определенного интеграла по переменному верхнему пределу равна значению подынтегральной функции в точке дифференцирования.
Доказательство. По определению производной
 ,
,
где
 . (21)
. (21)
Во втором слагаемом правой части (21) поменяем пределы интегрирования по формуле (6) и на основании теоремы 3 получим:

Величина 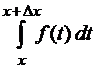 является площадью заштрихованной криволинейной трапеции (рис. 5). Поскольку функция
является площадью заштрихованной криволинейной трапеции (рис. 5). Поскольку функция  непрерывна, по теореме 6 о среднем значении найдется такая точка
непрерывна, по теореме 6 о среднем значении найдется такая точка  , для которой справедливо
, для которой справедливо
|
|
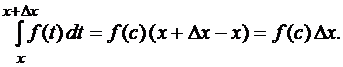
Тогда
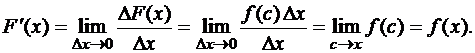
Теорема доказана.
Приведем примеры применения теоремы Барроу.
Пример 6.1. 
Пример 6.2. 
Пример 6.3.  , т.к. определенный интеграл с постоянными пределами – это постоянная величина.
, т.к. определенный интеграл с постоянными пределами – это постоянная величина.
Пример 6.4. 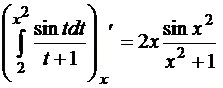 . Здесь мы имеем дело со сложной функцией:
. Здесь мы имеем дело со сложной функцией: 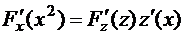 , где
, где  ,
,  .
.
Следствие. Любая непрерывная на промежутке  функция имеет на этом промежутке первообразную.
функция имеет на этом промежутке первообразную.
Действительно, если  – непрерывна, то существует
– непрерывна, то существует  . Но по теореме Барроу
. Но по теореме Барроу  , т.е.
, т.е.  – первообразная для
– первообразная для  . Таким образом,
. Таким образом,  – первообразная для
– первообразная для  .
.
Замечание. Первообразная непрерывной функции не всегда может быть выражена в терминах элементарных функций.
|
|
|

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!