Интегрирование функции одной переменной
Основные понятия неопределенного интеграла
Неопределенным интегралом функции f(x) называется множество всех первообразных функций F(x) + C.
Записывается:  .
.
Первообразной функцией для функции f(x) на промежутке (a; b) называется такая функция F(x), производная которой равна f(x) на рассматриваемом промежутке, то есть  .
.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
Имеет место теорема: две различные первообразные одной и той же функции, определенной в некотором промежутке, отличаются друг от друга в этом промежутке на некоторое постоянное слагаемое.
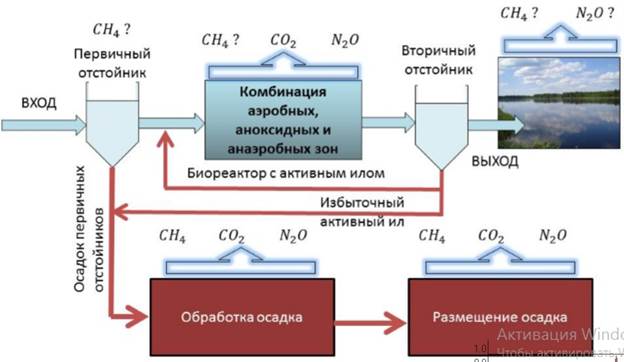
Функция f(x) называется непрерывной на отрезке [ a, b ], если:
1) она определена на этом множестве;
2) непрерывна в каждой точке этого отрезка, то есть 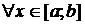 справедливо равенство
справедливо равенство 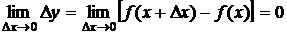 , где
, где  .
.
Теорема (условие существования неопределенного интеграла). Всякая непрерывная на отрезке [ a, b ] функция имеет на этом промежутке неопределенный интеграл.
Основные теоремы (свойства неопределенного интеграла):
1.  где C-const.
где C-const.
2.  .
.
3.  .
.
4.  где u, v, w – некоторые функции от х.
где u, v, w – некоторые функции от х.
5. 
6. (Инвариантность формулы интегрирования). Если 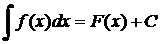 , то и
, то и  , где
, где 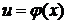 - произвольная функция, имеющая непрерывную производную.
- произвольная функция, имеющая непрерывную производную.
Ниже приводится таблица основных интегралов, которые используются при вычислениях неопределенных интегралов различных функций. Верность этой таблицы проверяется непосредственно дифференцированием.
Таблица 6.
| Интеграл
| Значение
| Интеграл
| Значение
|
|
| 
| 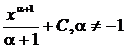
|
| 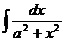
| 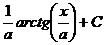
|
|
| 
| 
|
| 
| 
|
|
| 
| 
|
| 
| 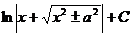
|
|
| 
| 
|
| 
| 
|
|
| 
| 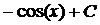
|
| 
| 
|
|
| 
| 
|
| 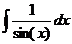
| 
|
|
| 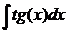
| 
|
| 
| 
|
|
| 
| 
|
| 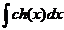
| 
|
|
| 
| 
|
| 
| 
|
|
| 
| 
|
| 
| 
|
Основные методы интегрирования
· Метод непосредственного интегрирования
Метод интегрирования основан на применении табличных интегралов, и называется непосредственным интегрированием. При этом данный интеграл может быть приведен к табличному с помощью тождественных преобразований подынтегральной функции и применения свойств неопределенного интеграла.
Пример 1. Найти интегралы функций:
a) 
b) 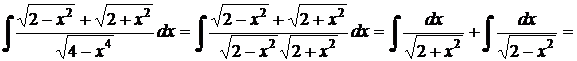
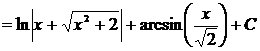 ;
;
с) 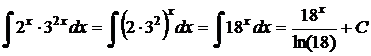 .
.
· Замена переменной
Этот метод интегрирования основан на введении новой переменной интегрирования. Приведем пример: пусть дана сложная функция f(x), где  - функция имеющая непрерывную производную
- функция имеющая непрерывную производную  . Применяется свойство инвариантности формулы интегрирования неопределенного интеграла, получаем:
. Применяется свойство инвариантности формулы интегрирования неопределенного интеграла, получаем:  .
.
Эта формула называется формулой замены переменной в неопределенном интеграле.
Пример 2. Найти интегралы функций:
a)  .
.
Решение.
 ;
;
b)  .
.
Решение.


 ;
;
с)  .
.
Решение.
 =
=  =
=  ;
;
d) 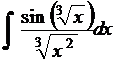 .
.
Решение.

 =
=  .
.
При интегрировании заменой переменной важно удачно сделать подстановку. Однако нельзя дать общее правило выбора замены переменной для интегрирования любой функции. Это можно сделать только для интегрирования отдельных классов функций: рациональных, тригонометрических и т.д. (интегрирование этих классов функций предложены в таблицах 3 – 7).
· Интегрирование по частям
Этот метод интегрирования основан на применении формулы дифференцирования произведения d(uv)=udv+vdu и вычислении затем интеграла 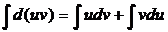 . Из этого равенства получаем формулу интегрирования по частям:
. Из этого равенства получаем формулу интегрирования по частям:  .
.
Пример 3. Найти интегралы функций:
a)  .
.
Решение.
Интегрируется по частям: пусть  ; тогда
; тогда  ,
,  . Следовательно,
. Следовательно,  .
.
Еще раз интегрируется по частям: пусть  тогда
тогда  . Получаем,
. Получаем,
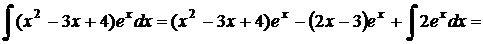
 ;
;
b)  .
.
Решение.
Интегрируется по частям: пусть 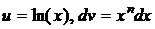 ; тогда
; тогда 
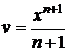 . Следовательно,
. Следовательно,


 ;
;
c)  .
.
Решение.
Интегрируется по частям: пусть  ; тогда
; тогда  ,
, 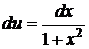 . Следовательно,
. Следовательно,  .
.
Получившийся интеграл вычисляется методом замены переменной:
 . Тогда
. Тогда 
 ;
;
d)  .
.
Решение.
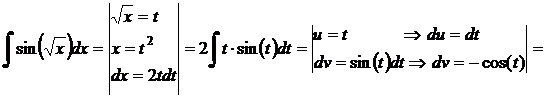

 .
.
е)  .
.
Решение.
Интегрируется по частям: пусть  ; тогда
; тогда 
 . Следовательно,
. Следовательно, 
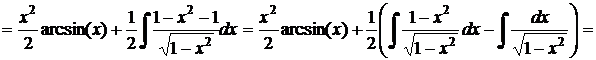
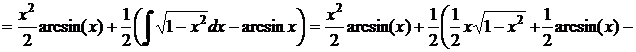
 ;
;
g) 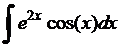 .
.
Решение.
Интегрируется по частям: пусть  тогда
тогда 
 . Следовательно,
. Следовательно,  .
.
Еще раз интегрируется по частям: пусть 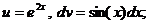 тогда
тогда 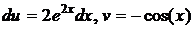 . Получается,
. Получается,

 =
=
=  .
.
Обозначается,  . Тогда
. Тогда  .
.
Следовательно, 
Приведем в таблице 7 некоторые распространённые случаи использования метода интегрирования по частям.
Таблица 7.
| вид интеграла
| метод интегрирования
|
 , ,
 , ,
 , ,
 . .
| За u принимается многочлен  , а за dv все остальные подынтегральные выражения. , а за dv все остальные подынтегральные выражения.
|
 , ,
 , ,
 , ,
 , ,
 . .
| За dv принимается  , а за u все остальные подынтегральные выражения. , а за u все остальные подынтегральные выражения.
|
 , ,
 , ,
 , ,
 . .
| Данные бесконечные интегралы, решаются как уравнения, после двукратного интегрирования по частям.
|
 , ,
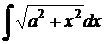 , a > 0. , a > 0.
| За dv принимается dх, а за u остальные подынтегральные выражения.
|
Решение.
 =
=  ;
;
b)  .
.
Решение.

 ;
;
c) 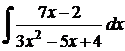 .
.
Решение.
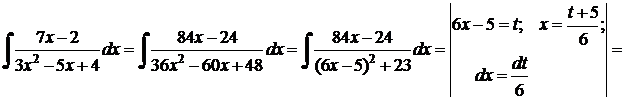

В таблице 8 приведены общие виды правильных рациональных дробей и способы их интегрирования с помощью замены переменной.
Таблица 8.
| №
| подынтегральное выражение
| преобразования
| замена
| dx
|
| I
| 
|
| 
| 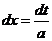
|
| II
| 
|
| 
| 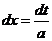
|
| III
| 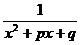
| 
| 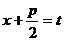
| 
|
| IV
| 
| 
| 
|  и раскладывается на сумму двух интегралов и раскладывается на сумму двух интегралов
|
m, n – натуральные числа (m ³ 2, n ³ 2) и D <0.
Подынтегральные выражения не вошедшие в таблицу 3 интегрируются с помощью метода неопределенных коэффициентов.
Теорема (метод неопределенных коэффициентов). Если  - правильная рациональная дробь, где знаменатель имеет вид:
- правильная рациональная дробь, где знаменатель имеет вид:
P(x) = (x - a)a…(x - b)b(x2 + px + q)l…(x2 + rx + s)m ) (причем множители типа x2+px+q неразложимы на действительные множители первой степени), то эта дробь может быть разложена на сумму простейших дробей:
 где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины.
где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины.
Пример 5. Найти интегралы функций:
a)  .
.
Решение.
 =
=  .
.
Подынтегральное выражение представляется в виде суммы простейших дробей  .
.
После освобождения от знаменателей, получается:
 .
.

Сгруппировываются члены с одинаковыми степенями:







В итоге получается:

b)  .
.
Решение. Так как дробь неправильная, то выделяется целая часть:
 6 x 5 – 8 x 4 – 25 x 3 + 20 x 2 – 76 x – 7 3 x 3 – 4 x 2 – 17 x + 6
6 x 5 – 8 x 4 – 25 x 3 + 20 x 2 – 76 x – 7 3 x 3 – 4 x 2 – 17 x + 6
6 x 5 – 8 x 4 – 34 x 3 + 12 x 2 2 x 2 + 3
9 x 3 + 8 x 2 – 76 x - 7
9 x 3 – 12 x 2 – 51 x +18
20 x 2 – 25 x – 25
Следовательно,

Для нахождения корней уравнения  применяем схему Горнера:
применяем схему Горнера:
| коэффициенты перед x
|
|
решение
|
|
| – 4
| – 17
|
|
|
|
|
| – 2
| –
|
| – 2
|
| – 1
| –
| –
|
| 1/3
|
| –
| –
| –
|
Получаются:  .
.
Следовательно, корни этого уравнения: 3; -2; 1/3.
Отсюда  .
.
Получившееся подынтегральное выражение раскладывается на элементарные дроби: 
 .
.
Применяем метод произвольных значений, суть которого состоит в том, что в полученное выражение подставляем поочередно (по числу неопределенных коэффициентов) значения х. Для упрощения вычислений принимают точки, при которых знаменатель дроби равен нулю. В нашем случае: 3, -2, 1/3. Получаем: 

 .
.
В итоге получаем:
 =
= 

Решение.


b)  .
.
Решение.

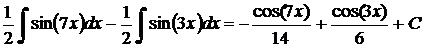 .
.
· Метод замены переменной
Пример 7. Найти интегралы функций:
а)  .
.
Решение.


в)  .
.
Решение.

 ;
;
с)  .
.
Решение.


Решение.


в)  .
.
Решение.

 ;
;
с)  .
.
Решение.

 .
.
Интеграл вычисляется методом неопределенных коэффициентов:
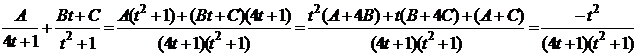 .
.


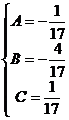 .
.
Получается: 


 .
.
Учитывая выше сказанное, представим основные типы тригонометрических функций в виде таблицы 9.
Таблица 9.
| №
| подынтегральное выражение
| замена
| 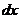
|
|
| 
| Универсальная замена
 
| 
|
|
| 
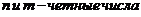
|  
| 
|
|
| 

| 

| 

|
|
| 
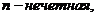 
| 

| 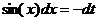
|
|
| 
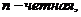

| 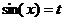
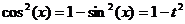
| 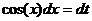
|
|
| 
|  , , 
 , , 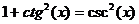
| 

|
|
| 
| Понижается степень по формуле

|
|
| 
| 
|
Здесь R – обозначение некоторой рациональной функции от переменных sin(x) и cos(x). Функции sec(x)=1/cos(x) и csc(x)=cosec(x)=1/sin(x).
Решение.


 ;
;
b) 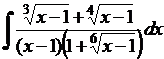 .
.
Решение.
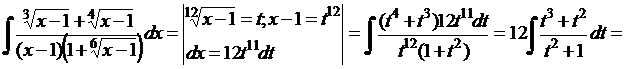
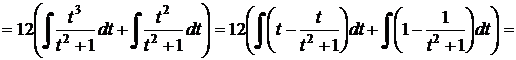
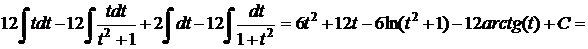
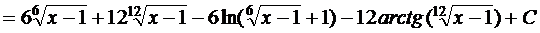 .
.
с) 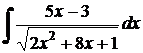 .
.
Решение.
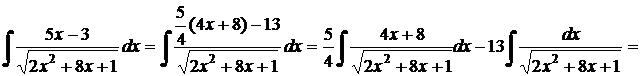
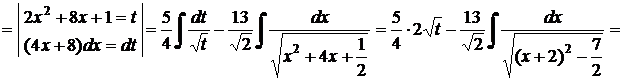
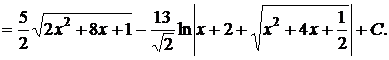
Таким образом, к первому типу можно отнести следующие подынтегральные выражения, представленные в таблице 10.
Таблица 10.
| №
| подынтегральное выражение
| преобразования
| замена
| dx
|
|
| 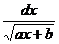
|
| 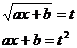
| 
|
|
| 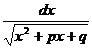
| 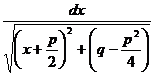
| 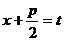
| 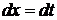
|
|
| 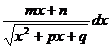
| 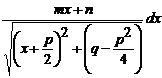
| 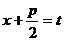
| 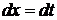
|
|
| 
|
| 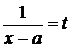 , ,
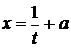
| 
|
|
| 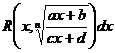 ,
где ,
где 
|
| 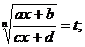
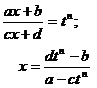
| 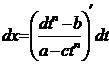
|
· Ко второму типу относят интегралы вида  , где Pn(x) – многочлен п- ой степени. Интеграл находится методом неопределённых коэффициентов, с помощью тождества:
, где Pn(x) – многочлен п- ой степени. Интеграл находится методом неопределённых коэффициентов, с помощью тождества: 
 =
= 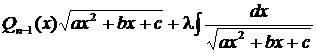 ,
,
где Qn-1(x) – многочлен степени равной п-1 с неопределёнными коэффициентами, λ – некоторый неопределённый коэффициент.
Пример 10. Найти интегралы функций:
а) 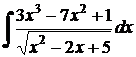 .
.
Решение.
Здесь n = 3, поэтому соответствующее тождество имеет вид:
 .
.
Продифференцируем полученное выражение:
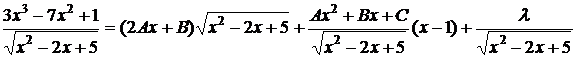 .
.
Умножим на 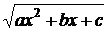 и сгруппируем коэффициенты при одинаковых степенях х:
и сгруппируем коэффициенты при одинаковых степенях х:
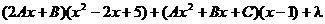 =
= 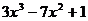
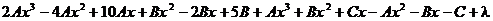 =
= 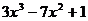
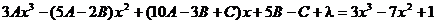
 .
.
Итого  =
=
= 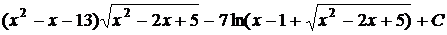 ;
;
b)  .
.
Решение.
Здесь n = 4, поэтому соответствующее тождество имеет вид:
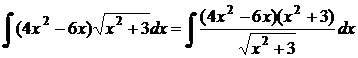
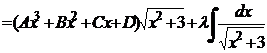 .
.
Дифференцируем полученное выражение:
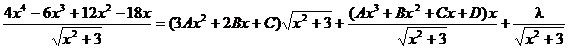 .
.
Перегруппировываем:
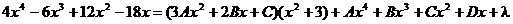
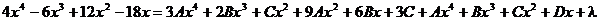
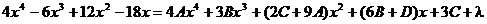
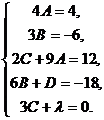

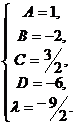



· К третьему типу относят интегралы вида 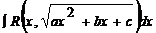 .
.
Интегрируются с помощью тригонометрической подстановки, которая называется подстановкой Эйлера. При необходимости выделяют под радикалом полный квадрат, т.е.  , и вводят обозначение:
, и вводят обозначение: 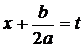 ,
, 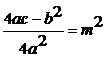 .
.
Пример 11. Найти интегралы функций:
a)  .
.
Решение.
 ;
;
b) 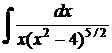 .
.
Решение.
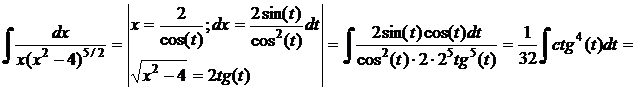
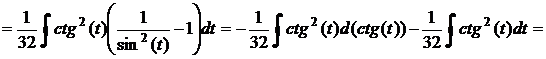

 ;
;
с) 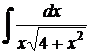 .
.
Решение.

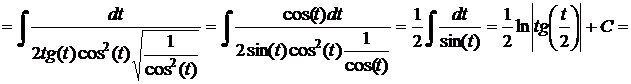

Таким образом, введя новые обозначения имеем следующие подынтегральные выражения, которые будут иметь соответствующие тригонометрические подстановки, представленные в таблице 11.
| №
| подынтегральное
выражение
| замена
| dt
|
|
| 
| 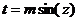 или или 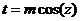
|   или или
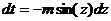
|
|
| 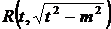
| 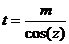 или или 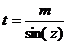
| 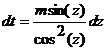 или или
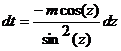
|
|
| 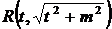
|  или или 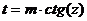
|  или или

|
Таблица 11.
Основные понятия и методы решения определенного интеграла
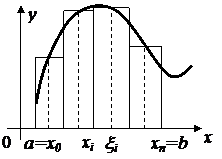 Пусть на отрезке [ a, b ] задана непрерывная функция f(x). Разобьём отрезок [ a, b ] произвольным образом на п частей точками
Пусть на отрезке [ a, b ] задана непрерывная функция f(x). Разобьём отрезок [ a, b ] произвольным образом на п частей точками  . На каждом отрезке
. На каждом отрезке 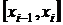 длины
длины 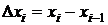 выберем произвольную точку
выберем произвольную точку 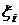 . Составим сумму
. Составим сумму 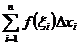 , называемую интегральной суммой для функции f(x) на отрезке [ a, b ].
, называемую интегральной суммой для функции f(x) на отрезке [ a, b ].
Рис. 23
Определённым интегралом от функции f(x) на отрезке [ a, b ] называется число равное пределу интегральных сумм при стремлении к нулю максимальной из длин отрезков разбиения: 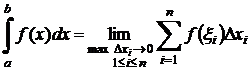 , этот предел конечен и не зависит от способов разбиения отрезка [ a, b ] на части и выбора точек
, этот предел конечен и не зависит от способов разбиения отрезка [ a, b ] на части и выбора точек 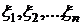 , на отрезках
, на отрезках  .
.
Определённый интеграл обозначается символом 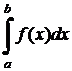 , где а называется нижним пределом, b называется верхним пределом, х называется переменной интегрирования, f(x) называется подынтегральной функцией, f(x)dx называется подынтегральным выражением, [ a, b ] – отрезок интегрирования.
, где а называется нижним пределом, b называется верхним пределом, х называется переменной интегрирования, f(x) называется подынтегральной функцией, f(x)dx называется подынтегральным выражением, [ a, b ] – отрезок интегрирования.
Пусть на отрезке [ a, b ] задана непрерывная функция 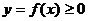 . Фигура, ограниченная сверху графиком функции
. Фигура, ограниченная сверху графиком функции 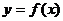 , снизу – осью Ox, сбоку прямыми x=a и x=b, называется криволинейной трапецией.
, снизу – осью Ox, сбоку прямыми x=a и x=b, называется криволинейной трапецией.
Геометрический смысл определённого интеграла: определённый интеграл равен площади «криволинейной трапеции» ограниченной функцией 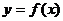 , осью О Y, и прямыми х=а и у=b.
, осью О Y, и прямыми х=а и у=b.
Теорема. Если функция f(x) непрерывна на отрезке [ a, b ], то определённый интеграл 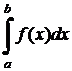 существует.
существует.
Отметим, что если оставить постоянным нижний предел интегрирования а, а верхний х изменить так, что бы  , то величина интеграла будет изменяться. Интеграл:
, то величина интеграла будет изменяться. Интеграл: 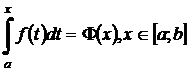 , называется определённым интегралом с переменным верхним пределом и является функцией верхнего предела х.
, называется определённым интегралом с переменным верхним пределом и является функцией верхнего предела х.
Теорема (Связь между неопределённым интегралом и определённым интегралами). Всякая непрерывная на отрезке [ a, b ] функция 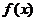 имеет первообразную, равную интегралу
имеет первообразную, равную интегралу  , и тогда, согласно определению неопределённого интеграла, имеет место равенство
, и тогда, согласно определению неопределённого интеграла, имеет место равенство 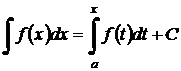 .
.
Теорема (Ньютона – Лейбница). Если функция F(x) – какая- либо первообразная от непрерывной функции f(x), то  – это выражение известно под названием формулы Ньютона – Лейбница [1].
– это выражение известно под названием формулы Ньютона – Лейбница [1].
Основные свойства определенного интеграла:
1. 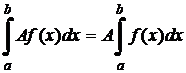 .
.
2. 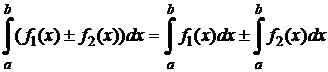 .
.
3. 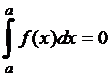 .
.
4. Если f(x) £ j(x) на отрезке [ a, b ] a < b, то  .
.
5. Если m и M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [ a, b ], то:  .
.
6. Теорема о среднем. Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка e такая, что 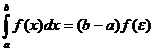 .
.
7. Для произвольных чисел a, b, c справедливо равенство: 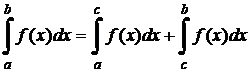 , где равенство выполняется, если существует каждый из входящих в него интегралов.
, где равенство выполняется, если существует каждый из входящих в него интегралов.
8.  .
.
9. 
Решение.
 .
.
Замена переменных
Пусть задан интеграл  , где f(x) – непрерывная функция на отрезке
, где f(x) – непрерывная функция на отрезке  . Введем новую переменную в соответствии с формулой x = j(t).
. Введем новую переменную в соответствии с формулой x = j(t).
1) j(a) = а, j(b) = b;
2) j(t) и j¢(t) непрерывны на отрезке [ a, b ];
3) f(j(t)) определена на отрезке [ a, b ], то  .
.
Тогда  .
.
Пример 13.  .
.
Решение.

Интегрирование по частям
Формула имеет вид:  .
.
Пример 14.  .
.
Решение.
 =
=  =
=  =
=
=  =
=  +
+  =0.
=0.
Несобственные интегралы
Решение.
 - не существует
- не существует  несобственный интеграл расходится.
несобственный интеграл расходится.
б) 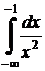 .
.
Решение.
 - интеграл сходится.
- интеграл сходится.
Объёмы тел вращения
Пусть кривая, задана уравнением y = f(x). Предположим, что функция f(x) непрерывна на отрезке [ a, b ]. Если соответствующую ей криволинейную трапецию с основаниями а и b вращать вокруг оси Ох, то получим так называемое тело вращения.


, где V – объем тела, полученного вращением криволинейной трапеции
0 £ y £ f(x), a £ x £ b вокруг оси О
х.
Рис. 25

, где V – объем тела, полученного вращением криволинейной трапеции
0£ x £ j(y),
c £ y £ d вокруг оси ОУ.
Рис. 26
. Площади плоских фигур, длины дуг кривых, площадь поверхности тела вращения рассмотрим в таблице 12.
Таблица 12.
| В прямоугольных координатах
| В полярных
координатах
|
y=f(x) на  или
x=φ(y)на или
x=φ(y)на 
|  
| |


 .
. .
.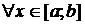 справедливо равенство
справедливо равенство 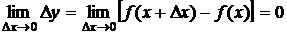 , где
, где  .
. где C-const.
где C-const. .
. .
. где u, v, w – некоторые функции от х.
где u, v, w – некоторые функции от х.
 , то и
, то и  , где
, где 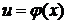 - произвольная функция, имеющая непрерывную производную.
- произвольная функция, имеющая непрерывную производную.
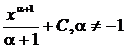
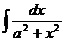
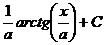







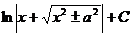





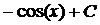




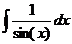

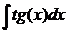





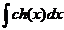










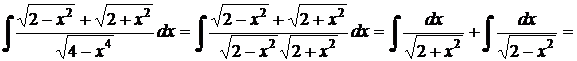
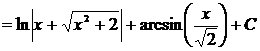 ;
;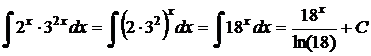 .
. - функция имеющая непрерывную производную
- функция имеющая непрерывную производную  . Применяется свойство инвариантности формулы интегрирования неопределенного интеграла, получаем:
. Применяется свойство инвариантности формулы интегрирования неопределенного интеграла, получаем:  .
. .
. ;
; .
.

 ;
; .
. =
=  =
=  ;
;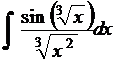 .
.
 =
=  .
.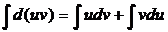 . Из этого равенства получаем формулу интегрирования по частям:
. Из этого равенства получаем формулу интегрирования по частям:  .
. .
. ; тогда
; тогда  ,
,  . Следовательно,
. Следовательно,  .
. тогда
тогда  . Получаем,
. Получаем,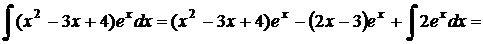
 ;
; .
.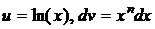 ; тогда
; тогда 
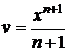 . Следовательно,
. Следовательно,

 ;
; .
. ; тогда
; тогда  ,
, 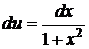 . Следовательно,
. Следовательно,  .
. . Тогда
. Тогда 
 ;
; .
.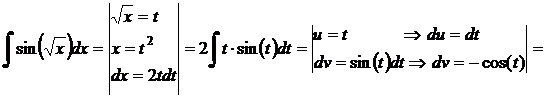

 .
. .
. ; тогда
; тогда 
 . Следовательно,
. Следовательно, 
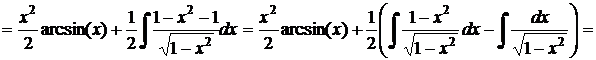
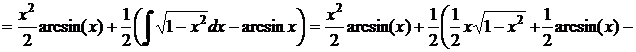
 ;
;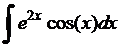 .
. тогда
тогда 
 . Следовательно,
. Следовательно,  .
.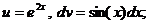 тогда
тогда 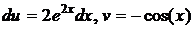 . Получается,
. Получается,
 =
= .
. . Тогда
. Тогда  .
.
 ,
,
 ,
,
 ,
,
 .
.
 , а за dv все остальные подынтегральные выражения.
, а за dv все остальные подынтегральные выражения.
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
 , а за u все остальные подынтегральные выражения.
, а за u все остальные подынтегральные выражения.
 ,
,
 ,
,
 ,
,
 .
.
 ,
,
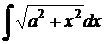 , a > 0.
, a > 0.
 =
=  ;
; .
.
 ;
;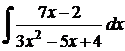 .
.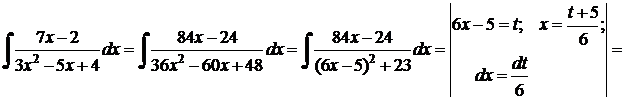



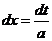

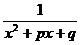

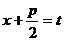




 и раскладывается на сумму двух интегралов
и раскладывается на сумму двух интегралов
 - правильная рациональная дробь, где знаменатель имеет вид:
- правильная рациональная дробь, где знаменатель имеет вид: где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины.
где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины. .
. .
. .
. .
.








 .
. 6 x 5 – 8 x 4 – 25 x 3 + 20 x 2 – 76 x – 7 3 x 3 – 4 x 2 – 17 x + 6
6 x 5 – 8 x 4 – 25 x 3 + 20 x 2 – 76 x – 7 3 x 3 – 4 x 2 – 17 x + 6
 применяем схему Горнера:
применяем схему Горнера: .
. .
.
 .
.

 .
.



 .
.
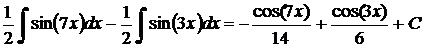 .
. .
.

 .
.
 ;
; .
.



 .
.
 ;
; .
.
 .
.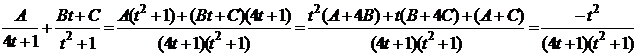 .
.
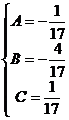 .
.


 .
.

















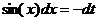
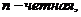

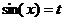
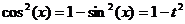
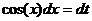

 ,
, 
 ,
, 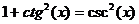








 ;
;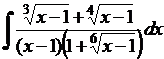 .
.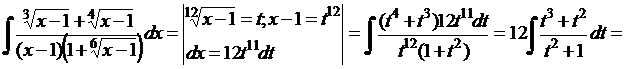
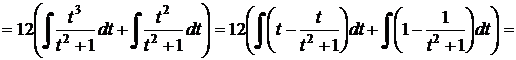
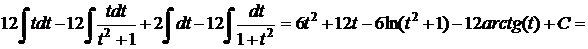
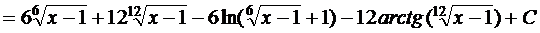 .
.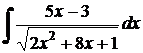 .
.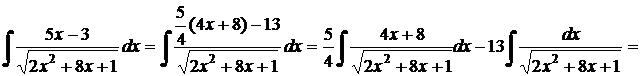
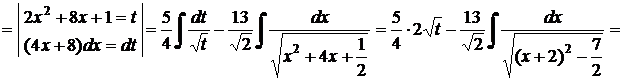
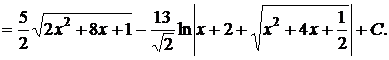
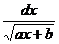
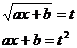

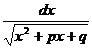
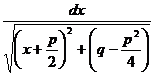
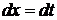
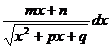
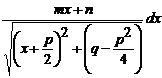

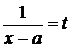 ,
,
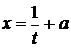

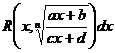 ,
где
,
где 
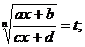
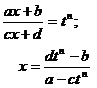
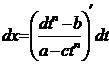
 , где Pn(x) – многочлен п- ой степени. Интеграл находится методом неопределённых коэффициентов, с помощью тождества:
, где Pn(x) – многочлен п- ой степени. Интеграл находится методом неопределённых коэффициентов, с помощью тождества: 
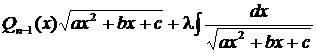 ,
,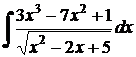 .
. .
.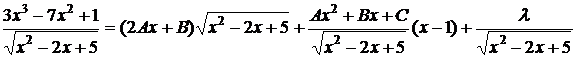 .
.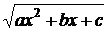 и сгруппируем коэффициенты при одинаковых степенях х:
и сгруппируем коэффициенты при одинаковых степенях х: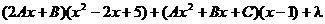 =
= 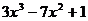
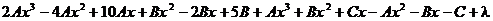 =
= 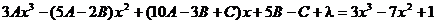
 .
. =
=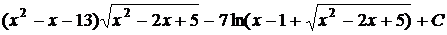 ;
; .
.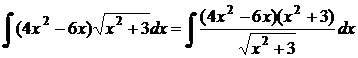
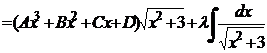 .
.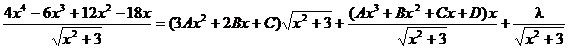 .
.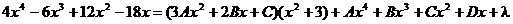
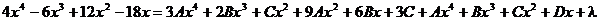
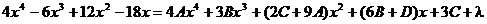
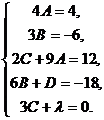
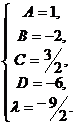


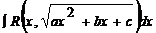 .
. , и вводят обозначение:
, и вводят обозначение: 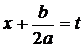 ,
, 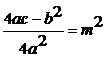 .
. .
. ;
;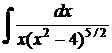 .
.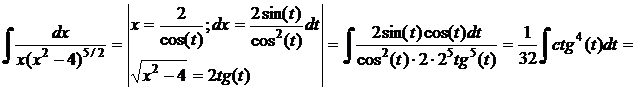
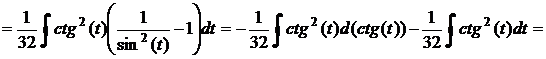

 ;
;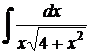 .
.
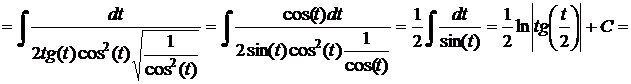


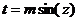 или
или 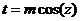

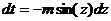
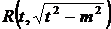
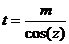 или
или 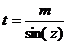
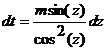 или
или
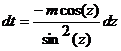
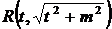
 или
или 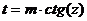
 или
или

 Пусть на отрезке [ a, b ] задана непрерывная функция f(x). Разобьём отрезок [ a, b ] произвольным образом на п частей точками
Пусть на отрезке [ a, b ] задана непрерывная функция f(x). Разобьём отрезок [ a, b ] произвольным образом на п частей точками  . На каждом отрезке
. На каждом отрезке 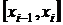 длины
длины 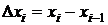 выберем произвольную точку
выберем произвольную точку 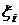 . Составим сумму
. Составим сумму 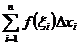 , называемую интегральной суммой для функции f(x) на отрезке [ a, b ].
, называемую интегральной суммой для функции f(x) на отрезке [ a, b ].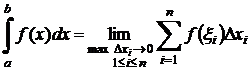 , этот предел конечен и не зависит от способов разбиения отрезка [ a, b ] на части и выбора точек
, этот предел конечен и не зависит от способов разбиения отрезка [ a, b ] на части и выбора точек 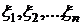 , на отрезках
, на отрезках  .
.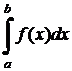 , где а называется нижним пределом, b называется верхним пределом, х называется переменной интегрирования, f(x) называется подынтегральной функцией, f(x)dx называется подынтегральным выражением, [ a, b ] – отрезок интегрирования.
, где а называется нижним пределом, b называется верхним пределом, х называется переменной интегрирования, f(x) называется подынтегральной функцией, f(x)dx называется подынтегральным выражением, [ a, b ] – отрезок интегрирования.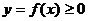 . Фигура, ограниченная сверху графиком функции
. Фигура, ограниченная сверху графиком функции 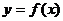 , снизу – осью Ox, сбоку прямыми x=a и x=b, называется криволинейной трапецией.
, снизу – осью Ox, сбоку прямыми x=a и x=b, называется криволинейной трапецией. , то величина интеграла будет изменяться. Интеграл:
, то величина интеграла будет изменяться. Интеграл: 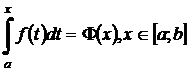 , называется определённым интегралом с переменным верхним пределом и является функцией верхнего предела х.
, называется определённым интегралом с переменным верхним пределом и является функцией верхнего предела х.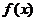 имеет первообразную, равную интегралу
имеет первообразную, равную интегралу  , и тогда, согласно определению неопределённого интеграла, имеет место равенство
, и тогда, согласно определению неопределённого интеграла, имеет место равенство 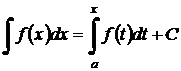 .
.  – это выражение известно под названием формулы Ньютона – Лейбница [1].
– это выражение известно под названием формулы Ньютона – Лейбница [1].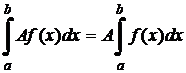 .
.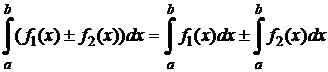 .
.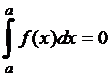 .
. .
. .
.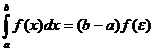 .
.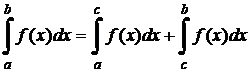 , где равенство выполняется, если существует каждый из входящих в него интегралов.
, где равенство выполняется, если существует каждый из входящих в него интегралов. .
.
 .
. , где f(x) – непрерывная функция на отрезке
, где f(x) – непрерывная функция на отрезке  . Введем новую переменную в соответствии с формулой x = j(t).
. Введем новую переменную в соответствии с формулой x = j(t). .
. .
. .
.
 .
. .
. =
=  =
=  =
= =
=  +
+  =0.
=0. - не существует
- не существует  несобственный интеграл расходится.
несобственный интеграл расходится.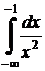 .
. - интеграл сходится.
- интеграл сходится.
 , где V – объем тела, полученного вращением криволинейной трапеции 0 £ y £ f(x), a £ x £ b вокруг оси О х.
, где V – объем тела, полученного вращением криволинейной трапеции 0 £ y £ f(x), a £ x £ b вокруг оси О х.

 , где V – объем тела, полученного вращением криволинейной трапеции 0£ x £ j(y),
, где V – объем тела, полученного вращением криволинейной трапеции 0£ x £ j(y),
 или
x=φ(y)на
или
x=φ(y)на 





