Понятие о логической функции

В математической логике основными понятиями являются логическая переменная и логическая функция.

Логическими переменными называются знаки (символы), которые принимают различные значения из соответствующей области. Такие переменные будем обозначать, например, буквами латинского алфавита: x₁, x₂,..., x_i, или y₁,y₂,..., y_i, или z₁, z₂,..., z_k. Область значений переменных может быть различной: нуль и единица {0,1}; нуль, плюс единица и минус единица {0,+1,-1}; нуль, единица, два {0,1,2} и др. Если область значений логических переменных содержит два значения, то такие логические переменные называют двоичными или булевыми, если же она содержит три значения, то их называют троичными, а если она содержит четыре более значений, то их называют многозначными переменными. Будем рассматривать только двоичные (булевы) переменные и под выражением “двоичные переменные” будем понимать логические двоичные переменные.

Совокупности значений переменных образуют наборы значений переменных, или просто наборы. Наборы значений логических переменных можно представить в виде двоичных чисел или в виде эквивалентов двоичных чисел. Например, переменные x₁, x₂, x₃, x₄ в зависимости от принимаемых значений образуют наборы: 0000, 0001, 0010,0011,0100,0101,0110,0111,1000,...,1111.

В общем виде набор значений переменных запишем как

,

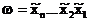где 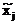(j=1,2,...,n) обозначает конкретное значение переменой x_j и равно либо 0, либо 1. Если каждая переменная принимает два значения, а число переменных равно n, то число различных наборов равно 2ⁿ. Переменные и наборы играют важную роль в понятии “логическая функция”.

Логической функцией называют функцию, зависящую от логических переменных и принимающую значения из того же множества, что и переменные, от которых она зависит. Логические функции двоичных (булевых) переменных принимают одно из двух значений: либо 0, либо 1.

Для обозначения логических функций будем пользоваться записями вида f (x), f (x_n, x_n-1,..., x₂, x₁), y_i(x), z(x), u(x) и другими, где в скобках указываются переменные, от которых зависит логическая функция.

Различные значения переменных логической функции образуют наборы значений этой функции. Наборы значений переменных зависят от порядка расположения переменных, поэтому для однозначного задания наборов введем порядок размещения переменных в наборе. Если не оговорено особо, переменные в наборе будем располагать справа налево в порядке возрастания индексов переменных. Например, набор w_i =1101 означает, что переменных в наборе четыре и переменные x₁=1, x₂=0, x₃= x₄=1.

Совокупность наборов, на которых определена логическая функция, образует область отправления (задания) этой функции. Для логической функции от n переменных эта область содержит 2 различных наборов. Множество значений, на которых определена логическая функция, образует область прибытия. Область прибытия булевых функций содержит два значения: “0” и “1”.

Определим число различных логических функций от n переменных. Из n переменных можно образовать 2ⁿ различных наборов.

На каждом наборе логическая функция может принимать значение либо 0, либо 1 независимо от ее значения на других наборах. Отсюда число различных логических функций определяется как произведение 2ⁿ чисел 2, т.е. N=2^{2 n} (таблица 2.1).

 

Таблица 2.1

Таблица соответствия логических функций, зависящих от n переменных

№	Набор значений	Логическая функция
п/п	переменных				...		...
	00...0
	00...1
	0...10
	0...11
	...
2n	1...11

 

Число различных логических функций возрастает с увеличением числа переменных и уже для функций пяти переменных составит огромное число - 4 294 966 296.

Всякая функция от меньшего числа переменных автоматически входит в число функций от большего числа переменных. Логическая функция f (x_n,..., x₂,x₁,) существенно зависит от переменной x_i, если имеет место соотношение

f (x_n,..., x_i+1, 0, x_i-1,..., x₁)¹ f (x_n,..., x_i+1, 1, x_i-1,..., x₁,).

В противном случае говорят, что функция f (x_n,..., x₂,x₁,) не зависит существенно от переменной x_i, т.е. x_i есть фиктивная переменная.

Функции n переменных, которые существенно зависят от всех переменных, называются невырожденными функциями от n переменных. Функции n переменных, которые фактически зависят от меньшего числа переменных, называются вырожденными.

Наборы переменных, на которых логическая функция принимает значение 1, будем называть единичными наборами, а наборы на которых функция принимает значение 0, будем называть нулевыми наборами.

Наряду с функциями, значения которых определены на всех 2ⁿ наборах, нередко возникает необходимость рассмотрения функций, значения которых определены только для части наборов. Наборы переменных, на которых значение функции не определено, будем называть неопределенными наборами. Логические функции, значения которых определены только на части наборов переменных, будем называть неполностью определенными функциями. Значения функций на условных наборах могут выбираться произвольным образом. В связи с этим неполностью определенную логическую функцию можно рассматривать как семейство полностью определенных логических функций, отличающихся друг от друга значениями на условных наборах. Если логическая функция содержит k условных наборов, то ей соответствует семейство, состоящее из 2^k различных полностью определенных функций, рабочие и запрещенные наборы которых полностью совпадают.

 

2.2. Способы задания логической функции

Для задания логической функции необходимо указать однозначное соответствие между наборами переменных и значениями функции (0 или 1). Логические функции могут быть заданы:

- словесным описанием;

- таблицами соответствия;

- номерами единичных и нулевых (неопределенных) наборов;

- формулами (аналитическими выражениями).

При словесном описании логической функции должны быть перечислены совокупности единичных и нулевых (неопределенных) наборов или указаны их характерные свойства. Например, логическая функция трех переменных задана единичными и нулевыми наборами. Единичные наборы переменных содержат две или более переменных, равных единице (011, 110, 101, 111), а все остальные наборы (000, 001, 010, 100) являются нулевыми.

Задание логических функций таблицами соответствия может быть выполнено несколькими вариантами. Для задания логической функции строится таблица, число строк которой равно числу различных наборов значений переменных, а число столбцов равно n+1. Первые n столбцов обозначаются символами переменных от которых зависит функция, а (n+1)-й столбец обозначается символом функции. В каждую строку такой таблицы записываются набор значений переменных и соответствующее ему значение функции. Например, функция трех переменных z(x) задана таблицей соответствия 2.2. Такую таблицу называют одновходовой таблицей соответствия.

 

Таблица 2.2

Таблица соответствия полностью и неполностью определенных логических функций z(x) и u(x)

w10	x3	x2	x1	z(x)	u(x)
					~
					~
					~

При задании неполностью определенных функций таблицами соответствия значения функции на условных наборах будем обозначать “-“ или “~” как показано в таблице соответствия 2.2 для логической функции u(x).

Рассмотренный способ задания функций приемлем для функций небольшого числа переменных, так как с увеличением числа переменных (n) количество наборов увеличится как 2ⁿ и таблица соответствия получается громоздкой.

Более компактным табличным способом задания логических функций является использование двухвходовых таблиц соответствия. Для построения такой таблицы переменные, от которых зависит логическая функция, разделяются на две примерно равные группы. Для образования групп переменных определяются всевозможные наборы их значений. Строки таблицы в произвольном порядке обозначаются наборами переменных первой группы, а столбцы таблицы - наборами переменных второй группы. Каждая клетка такой таблицы соответствует одному набору значений переменных, от которых зависит функция. В каждой клетке таблицы проставляется значение функции на соответствующем ей наборе значений переменных. Количество клеток такой таблицы соответствует числу всевозможных наборов значений переменных. Примером двухуровневой таблицы является таблица 2.3 в которой задана неполностью определенная логическая функция трех переменных u(x).

 

Таблица 2.3

Двухвходовая таблица соответствия для логической функции u(x)

x3	x3 x1
				~
	~	~

u(x)

Удобным способом задания логических функций является использование номеров единичных, нулевых или неопределенных наборов. Для этой цели любой набор будем рассматривать как представление целого неотрицательного числа в двоичной системе счисления, которая также оперирует с цифрами “0” и “1”. Целое число в двоичной системе счисления можно представить эквивалентным ему числом в десятичной или восьмеричной системах счисления. Эти числа будем называть номерами наборов в двоичной, восьмеричной или десятичной системах счисления, что позволит записывать в компактной форме наборы значений переменных логической функции. При этом будем полагать, что в двоичном числе младший разряд расположен справа. Например, набор 10011 может быть представлен десятичным числом

1×2⁴+0×2³+0×2²+1×2¹+1×2⁰=19,

а набор 1110 - числом

1×2³+1×2²+1×2¹+0×2=14.

Для представления набора (двоичного числа) в восьмеричной системе счисления необходимо его разделить на триады, начиная с младшего разряда, и каждую триаду записать цифрой в восьмеричной системе счисления. Например, набор 110011 может быть представлен восьмеричным числом 63, так как 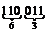® 63.

При разделении двоичного набора на триады крайняя левая триада может оказаться неполной. В этом случае значения старших недостающих разрядов двоичного набора принимаются равными нулю. Например, двоичному набору 1101110 соответствует восьмеричное числоь156, так как 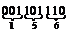® 156.

Удобство использования восьмеричной системы счисления состоит в том, что при записи двоичного набора в этой системе счисления сохраняется взаимооднозначное соответствие между разрядами восьмеричного числа и триадами двоичного набора (двоичного числа). Это позволяет легко переходить от задания двоичного набора значений переменных логических функций к восьмеричному числу и наоборот.

Для однозначного задания двоичного набора значений переменных необходимо указать его номер, систему счисления, в которой задан номер, порядок расположения переменных и размерность, т.е. количество переменных логических функций. Так, например, десятичному числу 25 соответствует набор 11001 при размерности 5 или набор 0011001 при размерности 7.

Условимся при задании логической функции номерами единичные наборы записывать в квадратных скобках, нулевые в круглых скобках, а неопределенные - в фигурных скобках. При задании логической функции номерами единичных и нулевых наборов первыми после квадратной скобки указываются номера единичных наборов, а затем в круглых скобках - номера нулевых наборов. За последней скобкой указывается основание системы счисления. Например логическая функция z(x) (таблица 2.2) может быть задана номерами единичных и нулевых наборов в виде

z(x₃, x_2, x₁)=[3, 5, 6, 7 (0, 1, 2, 4)]₁₀.

 

При задании неполностью определенной логической функции номерами единичных и неопределенных наборов, а затем в фигурных скобках - номера неопределенных наборов. Например, функция u(x) (табл.2.3) может быть задана выражением

u(x₃, x_2, x₁)=[1, 5, {3, 4,6}]₁₀.

При задании логической функции номерами нулевых и неопределенных наборов первыми после круглой скобки записываются номера нулевых наборов, а затем в фигурных скобках -номера неопределенных наборов. Например, функция, рассмотренная в предыдущем примере, может быть задана выражением

u(x₃, x_2, x₁)=[0, 2, 7 (3, 4, 6)]₁₀.

Необходимо отметить, что при таком способе задания, в зависимости от указанного порядка переменных, одними и теми же совокупностями номеров наборов могут быть заданы различные логический функции.

Произвольная логическая функция может быть задана в виде аналитического выражения (формулы), представляющего совокупность переменных, объединяемых определенными логическими операциями, которые будут введены в следующих параграфах.