ПРЕДМЕТ ИССЛЕДОВАНИЕ ОПЕРАЦИЙ
Исследование операций – это комплексная математическая дисциплина, занимающаяся построением, анализом и применением математических моделей принятия оптимальных решений при проведении операций.
Операция – система управляемых действий, объединенная единым замыслом и направленная на достижение определенной цели. Набор управляющих параметров (переменных) при проведении операции называется решением. Решение называется допустимым, если оно удовлетворяет набору определенных условий. Решение называется оптимальным, если оно допустимо и, по определенным признакам, предпочтительнее других, или, по крайней мере, не хуже. Признак предпочтения называется критерием оптимальности. Критерий оптимальности включает в себя целевую функцию и направление оптимизации или набор целевых функций и соответствующих направлений оптимизации. Целевая функция – это количественный показатель предпочтительности или эффективности решений. Направление оптимизации – это максимум (минимум), если наиболее предпочтительным является наибольшее (наименьшее) значение целевой функции. Например, критерием может быть максимизация прибыли либо минимизация расходов.
Математическая модель задачи ИСО включает в себя:
1) описание переменных, которые необходимо найти
2) описание критериев оптимальности
3) описание множества допустимых решений (ограничений, накладываемых на переменные).
Цель ИСО количественно и качественно обосновать принимаемое решение. Окончательное решение принимает ответственное лицо (либо группа лиц), называемое лицо, принимающее решение (ЛПР). Математическая модель задачи ИСО составляется в соответствии с представлениями ЛПР об этой задаче, т.e. в соответствии с его информационным состоянием.
Классификация задач ИСО
Классификация по зависимости параметров задачи от времени.
1.Статическая задача. Принятие решения происходит при условии, что все параметры задачи заранее известны и не изменяются, но времени. Процедура принятия решения осуществляется один раз.
2. Динамическая задача. В процессе принятия решения параметры задачи изменяются по времени. Процедура принятия решения осуществляется поэтапно и может быть представлена и виде процесса, зависящего от времени, в том числе непрерывно. Пример–навигационная задача.
Классификация в зависимости от достоверности информации о задаче.
1. Детерминированная задача. Все параметры задачи заранее известны. Для решения детерминированных задач в основном применяются методы математического программирования.
2. Недетерминированная задача. Не все параметры задачи заранее известны. Например, необходимо принять решение об управлении устройством, некоторые узлы которого могут непредсказуемо выходить из строя. Оптимальное решение недетерминированной задачи ИСО отыскать практически невозможно.
а) Стохастическая задача. Не все параметры задачи заранее известны, но имеются статистические данные о неизвестных параметрах (вероятности, функции распределения, математические ожидания и т.д.).
Для отыскания оптимального решения стохастической задачи применяется один и из следующих приемов:
1. искусственное сведение к детерминированной задаче (неизвестные параметры заменяются их средними значениями).
2. "оптимизация в среднем" (вводится и оптимизируется некоторый статистический критерий).
б) Задача в условиях (полной) неопределенности. Статистические данные о неизвестных параметрах отсутствуют. Задачи ИСО в условиях неопределенности в основном изучаются в рамках теории игр.
Классификация по виду критерия оптимальности.
Критерий оптимальности может иметь любой вид, в том числе неформализуемый. Наиболее распространенные формализуемые критерии оптимальности заключаются в оптимизации (минимизации либо максимизации) одной, либо нескольких скалярных целевых функций. Функция называется скалярной, если ее значением является некоторое число. Задача оптимизации скалярной функции на заданном множестве допустимых числовых решений называется задачей математического программирования. Наиболее изученными представителями однокритериальных задач математического программирования, т.е. задач с одной целевой функцией, являются следующие задачи (Рис.1):
· Задачи линейного программирования
· Задачи квадратичного программирования
· Задачи квадратичного программирования
· Задачи стохастического программирования
· Задача дискретного программирования
· Задача целочисленного программирования
· Задачи булева программирования
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Пример решения задачи линейного программирования
Рассмотрим на конкретном примере.Для изготовления изделий A, B, C и D, фабрика расходует в качестве сырья сталь и цветные металлы, имеющиеся в ограниченном количестве. Указанные изделия производят спомощью токарных и фрезерных станков. Определить план выпуска продукции, при котором будет достигнута максимальная прибыль. Необходимые данные приведены в таблице:
| Вид ресурса
| Объем ресурса
| Нормы расхода на одно изделие
|
A
| B
| C
| D
|
| Сталь, кг
|
|
|
|
|
|
| Цв. Металлы, кг
|
|
|
|
|
|
| Токарные станки, станко-час
|
|
|
|
|
|
| Фрезерные станки, станко-час
|
|
|
|
|
|
| Прибыль, ден. ед.
|
|
|
|
|
1) симплексным методом найти план выпуска продукции по видам с учетом имеющихся ограниченных ресурсов, который обеспечивал бы предприятию максимальный доход. Дать содержательный ответ, изложив экономический смысл всех переменных, участвующих в решении задачи;
2) сформулировать в экономических терминах двойственную задачу и составить еематематическую модель;
3) используя решение исходной задачи и соответствие между двойственными переменными, найти компоненты оптимального плана двойственной задачи — двойственные оценки у*i;
4) указать наиболее дефицитный и недефицитный (избыточный) ресурс, если он имеется;
5) с помощью двойственных оценок уi* обосновать рациональность оптимального плана, сопоставив оценку затрат fmin израсходованных ресурсов и максимальный доход zmaxот реализации готовой продукции по всему оптимальному плану и по каждому виду продукции в отдельности;
6) построить матрицу взаимозаменяемости ресурсов;
7) оценить целесообразность приобретения ∆bk = 3 единиц ресурса Рkпо цене сk=0,5 (к=3) за единицу;
8) установить размеры максимальной прибыли при изменении ресурса Р1, на -20 единиц, Р2— на 40 единиц, Р3 — на -10 единиц, Р4 — на 30 единиц. Оценить раздельное влияние этих изменений и суммарное их влияние на прибыль.
9) установить, целесообразно ли выпускать новую продукцию, на единицу которой ресурсы Р1, Р2и Р3 ,Р4 расходуются в количествах 12, 5, 17 и 9 единиц, а цена единицы готовой продукции составляет 5 ден. ед.
10) Компьютерная реализация:
10.1. Решить прямую и двойственную задачи. Построить диаграммы по полученным результатам (т.е. представить в виде диаграммы полученные прямое и двойственное решения)
10.2. Создать отчеты по результатам, пределам и устойчивости для прямой и двойственной задач. Дать пояснения к полученным в отчетах результатам и сравнить полученные результаты с результатами п. I. (т.е. с результатами, полученными без использования компьютера)
10.3. Решить задачи из п. I. 8) (4 задачи) и оценить раздельное и суммарное влияние этих изменений с помощью диаграммы.
Решить исходную задачу при условии, что решение должно быть целочисленным.
2.1. Обозначим через Х1, Х2, Х3, Х4 - количество изделий каждого вида соответственно, планируемого к выпуску, а через f – величину прибыли от реализации этих изделий. Тогда, учитывая значение прибыли от единицы продукции П1 = 4 ден. ед., П2= 2 ден. ед., П3= 4 ден. ед., П4= 3 ден. ед., запишем суммарную величину прибыли – целевую функцию в следующем виде:
f = 4Х1 + 2Х2 +4Х3 + 3Х4 (мах) (2.1)
Переменные Х1, Х2, Х 3, Х4 должны удовлетворять ограничениям, накладываемым на расход имеющихся в распоряжении предприятия ресурсов. Так, затраты ресурса P1(сталь, кг) на выполнение плана (Х1, Х2, Х3, Х4) составят (10Х1 + 20Х2 +15Х3+18Х4) ед., где 10Х1 – затраты ресурса P1 на выпуск Х1 ед. изделий А; 20Х2- затраты ресурса P2 на выпуск Х2 ед. изделий Б и т.д. Понятно, что указанная сумма не может превышать имеющийся запас P1 в 250 кг., т.е.
10Х1 + 20Х2 +15Х3+18Х4≤250 (2.2)
Аналогично получаем ограничение по расходу ресурса P2 (цветные металлы, кг.)
0Х1 + 5Х2 + 8Х3+ 7Х4 ≤40 (2.3)
ограничение по расходу ресурсов P3 (токарные станки, станко-час)
15Х1 + 18Х2 +12Х3+ 20Х4 ≤100 (2.4)
ограничение по расходу ресурсов P4 (фрезерные станки, станко-час)
8Х1 + 12Х2 + 11Х3+ 10Х4 ≤80. (2.5)
По смыслу задачи переменные Х1, Х2, Х 3, Х4 не могут выражаться отрицательными числами, т.е.
Хj≥0 (j=1,4) (2.6)
Соотношения (2.1) - (2.6) образуют экономико-математическую модель данной задачи.
Итак, математически задача сводится к нахождению числовых значений Х1*, Х2*, Х 3*, Х4* переменных Х1, Х2, Х 3, Х4, удовлетворяющих линейным неравенствам (2.2) - (2.6) и доставляющих максимум линейной функции (2.1)
Прежде чем решать задачу линейного программирования симплекс-методом, ее модель приводят к канонической форме. Основным признаком канонической формы является запись ограничений задачи в виде равенств. В нашем же случае ограничения (2.2) - (2.5) имеют вид неравенств типа "≤". Чтобы преобразовать их в эквивалентные уравнения, введем в левые части неравенств дополнительные (балансовые) неотрицательные переменные Х5, Х6, Х7, Х8, обозначающие разности между правыми и левыми частями этих неравенств. В результате модель можно записать в виде
f = 75Х1 + 35Х2 +40Х3 +20Х4 (мах) (2.7)
10Х1 + 20Х2 +15Х3+18Х4+ Х5 = 250
0Х1 + 5Х2 + 8Х3+ 7Х4 + Х6 = 40
15Х1 + 18Х2 +12Х3+ 20Х4 + Х7 = 100 (2.8)
8Х1 + 12Х2 + 11Х3+ 10Х4 + Х8 = 80
Хj≥0 (j=1,8) (2.9)
Заметим здесь же, что дополнительные переменные Х5, Х6, Х7, Х8имеют вполне определенный экономический смысл - это возможные остатки ресурсов соответственно P1, P2, P3 ,Р4. Их еще называют резервами.
Анализируя каноническую модель (2.7) - (2.9), замечаем, что каждая из переменных Х5, Х6, Х7, Х8 входит только в одно из уравнений системы (2.8). Это обстоятельство свидетельствует о том, что в системе (2.8) переменные Х5, Х6, Х7, Х8являются базисными, а остальные переменные Х1, Х2, Х3, Х4 - свободными. В связи с этим в первую симплекс-таблицу систему ограничительных уравнений (2.7) можно записать в виде, разрешенном относительно базиса Х5, Х6, Х7, Х8(табл. 2.1).
Таблица 2.1
| БП
|
| СП
|
| - Х1
| - Х2
| - Х3
| - Х4
|
| Х5=
|
|
|
|
|
|
| Х6=
|
|
|
|
|
|
| Х7=
|
| 15
|
|
|
|
| Х8=
|
|
|
|
|
|
| f
|
| -4
| -2
| -4
| -3
|
Все элементы столбца свободных членов положительны, поэтому содержащийся в табл. 2.1 план (0; 0; 0; 0; 250; 40; 100; 80), является опорным. Однако этот план не является оптимальным: в f — строке имеются отрицательные элементы. Чтобы получить опорный план, более близкий к оптимальному, выполним симплексное преобразование табл. 2.1. С этой целью выберем переменные, участвующие в преобразовании базиса Х5, Х6, Х7, Х8в новый базис. Наибольший по модулю отрицательный элемент (-4) f-строки указывает, что в новый базис следует ввести переменную Х1,т.е. в качестве разрешающего в предстоящем симплексном преобразовании надо взять первый столбец. Чтобы определить переменную, выводимую из базиса, составляем симплексные отношения и выбираем наименьшее из них
min(250/10; 40/0; 100/15; 80/8)= 100/15 = 6,667
Итак, из базиса надо исключить переменную, стоящую в третьей (разрешающей) строке, т.е. Х7. На пересечении разрешающих столбца и строки находится разрешающий элемент 15, с которым и выполняется симплексное преобразование (шаг жорданова исключения). В результате приходим к табл. 2.2.
В f-строке табл. 2.2 есть отрицательные элементы, значит, опорный план оптимальным не является.
Таблица 2.2
| БП
|
| СП
|
| - Х7
| - Х2
| - Х3
| - Х4
|
| Х5=
| 183,3
| -0,667
|
|
| 4,667
|
| Х6=
|
|
|
| 8
|
|
| Х1=
| 6,667
| 0,067
| 1,2
| 0,8
| 1,333
|
| Х8=
| 26,667
| -0,533
| 2,4
| 4,6
| 0,667
|
| F
| 26,667
| 0,267
| 2,8
| -0,8
| 2,333
|
Рассуждая аналогично предыдущему, устанавливаем, что для улучшения этого плана надо выполнить очередное симплексное преобразование с разрешающим элементом 8. В результате получаем табл. 2.3, в f-строке которой отрицательных элементов нет.
Таблица 2.3
| БП
|
| СП
|
| - Х7
| - Х2
| - Х6
| - Х4
|
| Х5=
| 148,3
| -0,667
| 3,625
| -0,875
| -1,46
|
| Х3=
|
|
| 0,625
| 0,125
| 0,875
|
| Х1=
| 2,667
| 0,0667
| 0,7
| -0,1
| 0,633
|
| Х8=
| 3,667
| -0,5333
| -0,475
| -0,575
| -4,69
|
| F
| 30,667
| 0,2667
| 3,3
| 0,1
| 3,033
|
Следовательно, опорный план (2,667; 0; 5; 0; 148,3; 0; 0; 3,667) является оптимальным, а соответствующее ему значение 30,667 целевой функции будет максимальным.
Итак, по оптимальному плану следует производить 2,667 ед. изделий А; 0 ед. изделий Б; 5 ед. изделий В; 0 ед. изделий С.
При этом предприятие получит максимальную прибыль в размере 30,667 ден. ед. Останутся неиспользованными 148,3 ед. ресурса P1 (сталь, кг.), и 3,667 ед. ресурса Р4 (фрезерные станки, станко-час), а ресурсы P2 и Р3 будут израсходованы полностью.
2.2. Двойственная переменная Yi. выступает коэффициентом при bi,следовательно, определяет зависимость целевой функции от изменения ресурсов bi на единицу.
Чтобы составить модель двойственной задачи, напишем матрицу исходной
задачи (2.1)- (2.6) в следующем виде:
Транспонируем матрицу (2.11). В результате получим матрицу (2.12) двойственной задачи:
По матрице (2.12) легко написать модель задачи, двойственной к исходной задаче:
φ = 250Y1 + 40Y2 +100Y3+ 80Y4 (min) (2.13)
10Y1 + 0Y2+ 15Y3+ 8Y4 ≥4
20Y1 + 5Y2 + 18Y3+ 12Y4 ≥2
15Y1 + 8Y2 +12Y3+ 11Y4 ≥4 (2.14)
18Y1 + 7Y2+ 20Y3+ 10Y4 ≥3
Yi≥0 (j=1,3) (2.15)
2.3. Из теорем двойственности следует, что если решена одна из пары двойственных задач, то одновременно найдено решение и другой задачи. Компоненты оптимального плана этой задачи находятся в строке целевой функции последней симплекс - таблицы решенной задачи.
В п. 1 мы нашли оптимальный план исходной задачи, его компоненты находятся в табл. 2.3. В f-строке этой же таблицы содержатся и компоненты Yi* оптимального плана двойственной задачи (2.13) - (2.15). Выписать компоненты Yi* поможет соответствие между переменными двойственных задач. Чтобы установить это соответствие, преобразуем ограничения-неравенства (2.14) в эквивалентные уравнения, вычитая из левых частей дополнительные неотрицательные переменные Y1, Y2 и Y3,Y4 равные разностям между левыми и правыми частями этих неравенств. Тогда модель (2.13)-- (2.15) запишется в виде
φ = 250Y1 + 40Y2 +100Y3+ 80Y4 (min)
10Y1 + 0Y2+ 15Y3+ 8Y4 – Y5= 4
20Y1 + 5Y2 + 18Y3+ 12Y4 – Y6= 2
15Y1 + 8Y2 +12Y3+ 11Y4 - Y7= 4
18Y1 + 7Y2+ 20Y3+ 10Y4 - Y8= 3
Yi≥0 (j=1,8)
В этой записи переменные Y5, Y6 и Y7, Y8 являются базисными, а Y1, Y2 и Y3, Y4 - свободными. В исходной задаче (2.7) - (2.9) переменные Х1, Х2 и Х3, Х4 являются свободными, a Х5, Х6 и Х7, Х8 - базисными.
Соответствие, о котором шла речь выше, устанавливают, сопоставляя базисным переменным одной задачи свободные переменные двойственной задачи и наоборот, т.е.
Х5ÛY1, Х6ÛY2, Х7ÛY3, Х8ÛY4, Х1ÛY5, Х2ÛY6 , Х3ÛY7, Х4ÛY8.
(2.16)
Воспользуемся соответствием (2.16) следующим образом. Как видно, переменная Y1 связана с переменной Х5 (поэтому их называют двойственными переменными), а в табл.2.3 переменная Х5 находится в базисе, значит, двойственная ей переменная Y1 на этом этапе расчетов является свободной и, как свободная переменная, равна нулю (в любой двойственной паре всегда одна переменная базисная, а другая свободная). Итак, Y1* = 0. Далее, Y2 соответствует Х6, а в табл.2.3 под Х6 в f- строке находится элемент 0,1, следовательно, Y2* = 0,1. Точно так же устанавливается, что Y3* = 0,2667; Y4* = 0; Y5* = 0; Y6* = 3,3; Y7* = 0; Y8* =3,033.
Из теорем двойственности следует, что экстремальные значения целевых функций разрешимых двойственных задач совпадают, поэтому φmin = fmax = = 30,667.
2.4. Оценки ресурсов Р2 и Р3являются положительными, следовательно эти виды сырья используется постоянно и является дефицитным. Наиболее дефицитным ресурсом будет ресурс Р3, так он имеет наибольшую оценку. Избыточным ресурсами является ресурсы Р1и Р4, так как их оценки равны нулю.
2.5. Чтобы определить изменение максимальной прибыли при изменении ресурсов, необходимо найти интервалы устойчивости двойственных оценок, в пределах которых они точно измеряют влияние ограничений на целевую функцию.Определим интервал устойчивости по отношению к ограничению по ресурсу 1-го вида. Для этого выпишем матрицу из коэффициентов при базисных неизвестных. Базисными переменными в оптимальном решении являются Х4, Х6, Х7, Х1. Матрица коэффициентов при этих переменных в системе ограничений имеет вид:

Обратная матрица 
|
| -0,875
| -0,667
|
|
|
| 0,125
|
|
|
|
| -0,1
| 0,0667
|
|
|
| -0,575
| -0,533
|
|
используя формулы 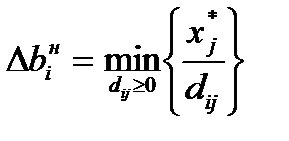 ;
;  , находим
, находим
 min (148,3/1)= 148,3
min (148,3/1)= 148,3
 ∞
∞
В соответствии с формулой:  , интервал устойчивости оценок по отношению к первому ресурсу примет вид: (250 – 148,3; 250 + ∞) = (101,7; ∞)
, интервал устойчивости оценок по отношению к первому ресурсу примет вид: (250 – 148,3; 250 + ∞) = (101,7; ∞)
Аналогично находим интервал устойчивости для остальных видов ресурсов.
 5/0,125 = 40
5/0,125 = 40  3,667/0,575 = 6,377
3,667/0,575 = 6,377
Р2:(40 – 40; 40 + 3,677) = (0; 43,677)
 2,6667/0,06667 = 40
2,6667/0,06667 = 40  3,667/0,533 = 6,875
3,667/0,533 = 6,875
Р3:(100 – 40; 100 + 6,875) = (60; 106,875)
 3,667/1 = 3,667
3,667/1 = 3,667  ∞
∞
Р4:(80 – 3,667; 80 + ∞) = (76,333; +∞)
Величина двойственной оценки численно равна изменению целевой функции при изменении соответствующего ресурса на одну единицу.
При увеличении ресурса Р2 на одну весовую единицу значение целевой функции оптимального плана увеличится на 0,1 ден. ед. При увеличении ресурса Р3 на одну весовую единицу значение целевой функции оптимального плана увеличится на 0,2667 ден. ед. Оценки ресурсов Р1 и Р4 равны нулю, следовательно данные ресурсы не является дефицитным, при их увеличении значение целевой функции не изменится. Оценка изделий Б и С больше нуля, следовательно производство данных изделий не будет рентабельным и при производстве одной единицы изделия Б значение целевой функции оптимального плана уменьшится на 3,3 ден. ед., а при производстве одной единицы изделия С значение целевой функции оптимального плана уменьшится на 3,033ден. ед.
2.6. Матрица коэффициентов взаимозаменяемости ресурсов:

|
| -0,875
| -0,667
|
|
|
| 0,125
|
|
|
|
| -0,1
| 0,0667
|
|
|
| -0,575
| -0,533
|
|
2.7. Оценим целесообразность приобретения Db= 3 единиц ресурса P3по цене c3=0,5 заединицу. Определим значение ∆ = y3 – C3 = 0,1 – 0,5 = -0,4. Увеличение прибыли при закупке 1 единицы ресурса Р3 меньше цены данного ресурса, следовательно не имеет смысла закупать данный ресурс.
2.8. Изменение второго вида ресурса не находится в пределах устойчивости оценок, следовательно мы не можем оценить влияние изменения на целевую функцию. Изменения ресурсов 1, 3, 4 находятся в пределах устойчивости оценок, то их раздельное влияние на величину прибыли, Dfimax определяется произведением оценки yi и величины изменения Dbi.
Df1max=Db1·y1= -20· 0= 0 ден. ед.
Df3max=Db3·y3= -10·0,2667 = -2,667 ден. ед.
Df4max=Db4·y4= 30·0 = 0 ден. ед.
Суммарное влияние Dfmax=Df1max+Df3max +Df4max= 0 – 2,667 + 0= -2,667 ден. ед.
2.9. Установим, целесообразно ли выпускать новую продукцию, на единицу которой ресурсы Р1, Р2 и Р3, Р4 расходуются в количествах 12; 5; 17 и 9 единиц, а цена единицы готовой продукции составляет 5 ед. Для этого вычисляем характеристику:
 (12·0+ 5·0,1+ 17·0,2667+ 9) – 5 = 0,0339 > 0
(12·0+ 5·0,1+ 17·0,2667+ 9) – 5 = 0,0339 > 0
Так как прибыль не превышает затраты то введение в план производства нового изделия не целесообразно.
3.5.
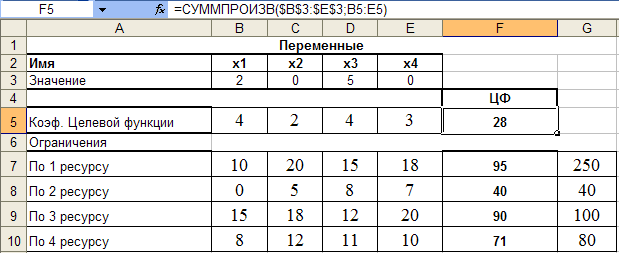
Оптимальное значение целевой функции при целочисленном решении будет 28 ден.ед., что на 2,667 ден. ед. меньше, чем при нецелочисленном решении.
Заключение
По произведенным нами расчетам можем сказать следующее. Согласно оптимальному плану рассматриваемой нами задачи следует производить 2,667 ед. изделий А; 0 ед. изделий Б; 5 ед. изделий В; 0 ед. изделий С. При этом предприятие получит максимальную прибыль в размере 30,667 ден. ед. Останутся неиспользованными 148,3 ед. ресурса P1 (сталь, кг.), и 3,667 ед. ресурса Р4 (фрезерные станки, станко-час), а ресурсы P2 и Р3 будут израсходованы полностью.
Основываясь на решении двойственной задачи, можем отметить, оценки ресурсов Р2 и Р3являются положительными, следовательно эти виды сырья используется постоянно и является дефицитным. Наиболее дефицитным ресурсом будет ресурс Р3, так он имеет наибольшую оценку. Избыточным ресурсами является ресурсы Р1и Р4, так как их оценки равны нулю.
Величина двойственной оценки численно равна изменению целевой функции при изменении соответствующего ресурса на одну единицу. При увеличении ресурса Р2 на одну весовую единицу значение целевой функции оптимального плана увеличится на 0,1 ден. ед. При увеличении ресурса Р3 на одну весовую единицу значение целевой функции оптимального плана увеличится на 0,2667 ден. ед. Оценки ресурсов Р1 и Р4 равны нулю, следовательно данные ресурсы не является дефицитным, при их увеличении значение целевой функции не изменится. Оценка изделий Б и С больше нуля, следовательно производство данных изделий не будет рентабельным и при производстве одной единицы изделия Б значение целевой функции оптимального плана уменьшится на 3,3 ден. ед., а при производстве одной единицы изделия С значение целевой функции оптимального плана уменьшится на 3,033 ден. ед.
Реализовывать новую товарную группу, на единицу которой ресурсы Р1, Р2 и Р3, Р4 расходуются в количествах 14; 20; 25; 90 единиц, а цена реализации составляет 10 ден. ед. не целесообразно, так как затраты на её реализацию не превышают прибыль при её продаже.
Увеличение прибыли при закупке 1 единицы ресурса Р3 меньше цены данного ресурса, следовательно не имеет смысла закупать данный ресурс.
Изменение второго вида ресурса не находится в пределах устойчивости оценок, следовательно мы не можем оценить влияние изменения на целевую функцию. Изменения ресурсов 1, 3, 4 находятся в пределах устойчивости оценок, то их раздельное влияние на величину прибыли, Dfimax определяется произведением оценки yi и величины изменения Dbi.
Df1max0ден. ед.; Df3max= -2,667 ден. ед.; Df4max= 0 ден. ед.
Суммарное влияние Dfmax=Df1max+Df3max +Df4max= 0 – 2,667 + 0= -2,667 ден. ед.
При введении в производство нового вида продукции прибыль не превышает затраты, следовательно нет смысла внедрять новый вид продукции.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
[1] Taha, Н. Operationsresearch
[2] Орлов А.И., Основы теории принятия решений. Учебное пособие. Москва, 2002.
[3] Новикова, Н.А. Исследование Операций, Минск.2010
[4] Лемешко Б.Ю., Теория игр и исследование операций. Новосибирский государственный технический университет, 2013
[5] Алексеев Е.Р., Павловская Е.В., Чеснокова О.В., Ломовцева О., Решение задач оптимизации и линейного программирования с помощью современных программных средств.
ПРЕДМЕТ ИССЛЕДОВАНИЕ ОПЕРАЦИЙ
Исследование операций – это комплексная математическая дисциплина, занимающаяся построением, анализом и применением математических моделей принятия оптимальных решений при проведении операций.
Операция – система управляемых действий, объединенная единым замыслом и направленная на достижение определенной цели. Набор управляющих параметров (переменных) при проведении операции называется решением. Решение называется допустимым, если оно удовлетворяет набору определенных условий. Решение называется оптимальным, если оно допустимо и, по определенным признакам, предпочтительнее других, или, по крайней мере, не хуже. Признак предпочтения называется критерием оптимальности. Критерий оптимальности включает в себя целевую функцию и направление оптимизации или набор целевых функций и соответствующих направлений оптимизации. Целевая функция – это количественный показатель предпочтительности или эффективности решений. Направление оптимизации – это максимум (минимум), если наиболее предпочтительным является наибольшее (наименьшее) значение целевой функции. Например, критерием может быть максимизация прибыли либо минимизация расходов.
Математическая модель задачи ИСО включает в себя:
1) описание переменных, которые необходимо найти
2) описание критериев оптимальности
3) описание множества допустимых решений (ограничений, накладываемых на переменные).
Цель ИСО количественно и качественно обосновать принимаемое решение. Окончательное решение принимает ответственное лицо (либо группа лиц), называемое лицо, принимающее решение (ЛПР). Математическая модель задачи ИСО составляется в соответствии с представлениями ЛПР об этой задаче, т.e. в соответствии с его информационным состоянием.
Классификация задач ИСО
Классификация по зависимости параметров задачи от времени.
1.Статическая задача. Принятие решения происходит при условии, что все параметры задачи заранее известны и не изменяются, но времени. Процедура принятия решения осуществляется один раз.
2. Динамическая задача. В процессе принятия решения параметры задачи изменяются по времени. Процедура принятия решения осуществляется поэтапно и может быть представлена и виде процесса, зависящего от времени, в том числе непрерывно. Пример–навигационная задача.
Классификация в зависимости от достоверности информации о задаче.
1. Детерминированная задача. Все параметры задачи заранее известны. Для решения детерминированных задач в основном применяются методы математического программирования.
2. Недетерминированная задача. Не все параметры задачи заранее известны. Например, необходимо принять решение об управлении устройством, некоторые узлы которого могут непредсказуемо выходить из строя. Оптимальное решение недетерминированной задачи ИСО отыскать практически невозможно.
а) Стохастическая задача. Не все параметры задачи заранее известны, но имеются статистические данные о неизвестных параметрах (вероятности, функции распределения, математические ожидания и т.д.).
Для отыскания оптимального решения стохастической задачи применяется один и из следующих приемов:
1. искусственное сведение к детерминированной задаче (неизвестные параметры заменяются их средними значениями).
2. "оптимизация в среднем" (вводится и оптимизируется некоторый статистический критерий).
б) Задача в условиях (полной) неопределенности. Статистические данные о неизвестных параметрах отсутствуют. Задачи ИСО в условиях неопределенности в основном изучаются в рамках теории игр.
Классификация по виду критерия оптимальности.
Критерий оптимальности может иметь любой вид, в том числе неформализуемый. Наиболее распространенные формализуемые критерии оптимальности заключаются в оптимизации (минимизации либо максимизации) одной, либо нескольких скалярных целевых функций. Функция называется скалярной, если ее значением является некоторое число. Задача оптимизации скалярной функции на заданном множестве допустимых числовых решений называется задачей математического программирования. Наиболее изученными представителями однокритериальных задач математического программирования, т.е. задач с одной целевой функцией, являются следующие задачи (Рис.1):
· Задачи линейного программирования
· Задачи квадратичного программирования
· Задачи квадратичного программирования
· Задачи стохастического программирования
· Задача дискретного программирования
· Задача целочисленного программирования
· Задачи булева программирования
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ





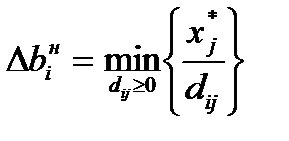 ;
;  , находим
, находим min (148,3/1)= 148,3
min (148,3/1)= 148,3 ∞
∞ , интервал устойчивости оценок по отношению к первому ресурсу примет вид: (250 – 148,3; 250 + ∞) = (101,7; ∞)
, интервал устойчивости оценок по отношению к первому ресурсу примет вид: (250 – 148,3; 250 + ∞) = (101,7; ∞) 5/0,125 = 40
5/0,125 = 40  3,667/0,575 = 6,377
3,667/0,575 = 6,377 2,6667/0,06667 = 40
2,6667/0,06667 = 40  3,667/0,533 = 6,875
3,667/0,533 = 6,875 3,667/1 = 3,667
3,667/1 = 3,667  ∞
∞ (12·0+ 5·0,1+ 17·0,2667+ 9) – 5 = 0,0339 > 0
(12·0+ 5·0,1+ 17·0,2667+ 9) – 5 = 0,0339 > 0



