СФЕРИЧЕСКАЯ ФУНКЦИЯ
 ,
,
 ;
;  ;
;  ;
; 
Описывает угловую зависимость состояния объекта в сферической системе координат  .
.
Используется для описания вращательного движения, в теории излучения и рассеяния волн и частиц, в теории потенциала.
Определяется как собственная функция оператора момента импульса и оператора Лапласа.
Число l связано с модулем момента импульса, m – с его проекцией на ось z. Проекция вектора не может быть больше его модуля, поэтому  , для проекции возможны положительные и отрицательные значения.
, для проекции возможны положительные и отрицательные значения.
Набор  образует полный ортонормированный базис на единичной сфере.
образует полный ортонормированный базис на единичной сфере.
Момент импульса ЧАСТИЦЫ
В классической механике
 ,
,
 – радиус-вектор частицы,
– радиус-вектор частицы,  – импульс. Направление L определяется правилом правого винта.
– импульс. Направление L определяется правилом правого винта.

В декартовых координатах
 ,
,
 ,
,
 ,
,
 .
.
Формулы переходят друг в друга при циклической перестановке
 .
.
В квантовой механике величины заменяются операторами
 ,
, 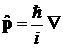 ,
,
 .
.
Оператор градиента
 , (7.1)
, (7.1)
n k – единичные орты, направленные в сторону перемещения точки при бесконечно малом увеличении соответствующего аргумента.
Операторы момента импульса
 ,
,
 ,
,
 ,
,
 ,
,
 . (7.2)
. (7.2)
Формулы переходят друг в друга при циклической перестановке
 .
.
Сферические координаты
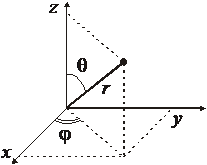
 ,
,  ,
,  . (7.3)
. (7.3)

Оператор градиента
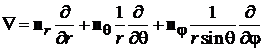 , (П.8.1)
, (П.8.1)
 – единичные орты. Операторы момента импульса
– единичные орты. Операторы момента импульса
 , (7.4)
, (7.4)
 . (7.5)
. (7.5)
Оператор Лапласа
Выражается через квадрат момента импульса
 , (7.6)
, (7.6)
определяет кинетическую энергию частицы.
Радиальная часть оператора Лапласа
 . (7.7)
. (7.7)
Перестановочное соотношение операторов (коммутатор)
 .
.
Предполагается, что правее каждого слагаемого находится функция, на которую действуют операторы:
 .
.
Выполняются
 ,
,
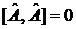 .
.
Если операторы коммутируют, т. е. их можно переставлять  , то соответствующие им физические величины измеримы одновременно с неограниченной точностью. Если коммутатор операторов не равен нулю, то чем точнее измеряется одна величина, тем больше неустранимая погрешность другой величины.
, то соответствующие им физические величины измеримы одновременно с неограниченной точностью. Если коммутатор операторов не равен нулю, то чем точнее измеряется одна величина, тем больше неустранимая погрешность другой величины.
Для операторов момента импульса
 ,
,
 ,
,
 ,
,
 . (7.8)
. (7.8)
Определенные значения имеют одновременно квадрат модуля момента импульса  и одна из его проекций
и одна из его проекций  .
.
Повышающий и понижающий операторы
 ,
,
 . (7.9)
. (7.9)
Действуя на сферическую функцию  , операторы
, операторы  изменяют на единицу число m, т. е. проекцию вектора момента импульса на ось z.
изменяют на единицу число m, т. е. проекцию вектора момента импульса на ось z.
Выполняются
 ,
,
 , (7.11)
, (7.11)
 . (7.12)
. (7.12)
Доказательство (7.12):

 ,
,
где использовано
 . (7.8)
. (7.8)
УРАВНЕНИЕ СферическОЙ функциИ
 является собственной функцией оператора квадрата момента импульса
является собственной функцией оператора квадрата момента импульса
 , (7.13)
, (7.13)
где 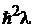 – собственное значение оператора
– собственное значение оператора 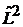 . Если объект находится в состоянии
. Если объект находится в состоянии  , то квадрат момента импульса равен
, то квадрат момента импульса равен  .
.
С учетом
 , (7.5)
, (7.5)
уравнение для сферической функции
 . (7.14)
. (7.14)
Ищем решение уравнения  и собственное значение λ.
и собственное значение λ.
Разделение переменных
Слагаемые (7.14) имеют производные от разных аргументов, поэтому аргументы решения разделяются
 .
.
Подставляем в уравнение, умноженное слева на  , и группируем слагаемые по их аргументам
, и группируем слагаемые по их аргументам
 .
.
Левая и правая стороны зависят от разных аргументов, поэтому они равны постоянной m. В результате получаем независимые уравнения
 , (7.15)
, (7.15)
 . (7.16)
. (7.16)
Решение уравнения (7.15)
1. Уравнение (7.15) является уравнением Гельмгольца и имеет решение
 .
.
2. Однозначность решения накладывает условие периодичности по углу 
 .
.
Получаем
 ,
,
откуда
 ,
,  ,
,
 – магнитное число,
– магнитное число,
 .
.
3. Квадрат модуля функции состояния является плотностью вероятности состояния и удовлетворяет условию нормировки
 ,
,
тогда
 ,
,
 . (7.17)
. (7.17)
На основании
 (1.43)
(1.43)
выполняется условие ортонормированности
 . (7.18)
. (7.18)
4. Для оператора проекции момента импульса
 , (7.4)
, (7.4)
выполняется
 ,
,
 . (7.19)
. (7.19)
Следовательно, 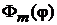 и
и  – собственные функции оператора проекции момента импульса на ось z с собственным значением
– собственные функции оператора проекции момента импульса на ось z с собственным значением  . В состоянии, описываемом функцией
. В состоянии, описываемом функцией 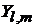 , измерение проекции момента импульса на ось z дает
, измерение проекции момента импульса на ось z дает
 .
.
Значение l в уравнении 
1. Оператором
 (7.11)
(7.11)
действуем на  и используем
и используем
 , (7.19)
, (7.19)
получаем
 .
.
Операторы  переводят состояние с собственным значением m в состояния с собственными значениями
переводят состояние с собственным значением m в состояния с собственными значениями  , т. е.
, т. е.  – повышающий оператор,
– повышающий оператор,  – понижающий оператор.
– понижающий оператор.
2. Проекция вектора не превышает его модуль. Если
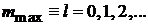 ,
,
то нет состояний с 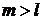 , тогда действие повышающего оператора на состояние с максимальной проекцией
, тогда действие повышающего оператора на состояние с максимальной проекцией
 .
.
3. Действуем на  оператором
оператором
 . (7.12)
. (7.12)
Используем
 (7.19)
(7.19)
и
 , (7.13)
, (7.13)
тогда

и находим
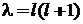 .
.
4. В результате
 ,
,
 , (7.20)
, (7.20)
где
 – магнитное число;
– магнитное число;
 – орбитальное число;
– орбитальное число;
 – проекция орбитального момента на ось z;
– проекция орбитального момента на ось z;
 – модуль орбитального момента.
– модуль орбитального момента.
Сферическая функция
В результате
 , (7.24)
, (7.24)
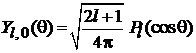 . (7.24а)
. (7.24а)
Из
 (6.120)
(6.120)
следует соотношение между состояниями с противоположными проекциями
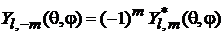 . (7.25)
. (7.25)
Используем
 , (1.43)
, (1.43)
 , (6.123)
, (6.123)
получаем условие ортонормированности
 . (7.27)
. (7.27)
Инверсия координат
Заменяем
 ,
,

 ,
,
 ,
,
 ,
,  ,
,
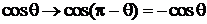 ,
,
 ,
,
получаем
 . (7.28)
. (7.28)
Четность состояния, описываемого сферической функцией, совпадает с четностью орбитального числа l.
Частные выражения
Используем
 , (7.24)
, (7.24)
и находим
 ,
,
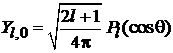 ,
,
 ,
,
 ,
,
 ,
,
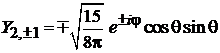 ,
,
 . (7.29)
. (7.29)
При 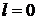 нет зависимости от углов – центрально-симметричное распределение;
нет зависимости от углов – центрально-симметричное распределение;
При  нет зависимости от угла φ – осесимметричное распределение.
нет зависимости от угла φ – осесимметричное распределение.
Плотность вероятности
Рекуррентные соотношения
1. Соотношение
 . (6.127)
. (6.127)
умножаем на
 ,
,
учитываем
 (7.24)
(7.24)
и получаем
 . (7.32)
. (7.32)
2. В (6.125) заменяем  , тогда
, тогда
 .
.
Умножаем на

и находим

 . (7.33)
. (7.33)
3. В (7.33) заменяем  , комплексно сопрягаем, используем
, комплексно сопрягаем, используем
 , (7.25)
, (7.25)
 ,
,
получаем
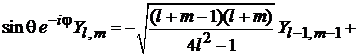
 . (7.34)
. (7.34)
Первое слагаемое
При изменении радиуса
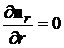 ,
,  ,
,  ,
,
тогда
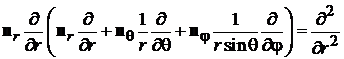 .
.
Второе слагаемое
При изменении угла θ, аналогично углу φ в полярных координатах:
 ,
,  ,
,  ,
,
тогда
 .
.

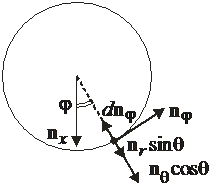
Третье слагаемое
При изменении угла φ используем
 ,
,  ,
,  ,
,
находим
 .
.
В результате оператор Лапласа в сферических координатах
 . (П.8.3)
. (П.8.3)
СФЕРИЧЕСКАЯ ФУНКЦИЯ
 ,
,
 ;
;  ;
;  ;
; 
Описывает угловую зависимость состояния объекта в сферической системе координат  .
.
Используется для описания вращательного движения, в теории излучения и рассеяния волн и частиц, в теории потенциала.
Определяется как собственная функция оператора момента импульса и оператора Лапласа.
Число l связано с модулем момента импульса, m – с его проекцией на ось z. Проекция вектора не может быть больше его модуля, поэтому  , для проекции возможны положительные и отрицательные значения.
, для проекции возможны положительные и отрицательные значения.
Набор  образует полный ортонормированный базис на единичной сфере.
образует полный ортонормированный базис на единичной сфере.
Момент импульса ЧАСТИЦЫ
В классической механике
 ,
,
 – радиус-вектор частицы,
– радиус-вектор частицы,  – импульс. Направление L определяется правилом правого винта.
– импульс. Направление L определяется правилом правого винта.

В декартовых координатах
 ,
,
 ,
,
 ,
,
 .
.
Формулы переходят друг в друга при циклической перестановке
 .
.
В квантовой механике величины заменяются операторами
 ,
, 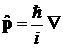 ,
,
 .
.
Оператор градиента
 , (7.1)
, (7.1)
n k – единичные орты, направленные в сторону перемещения точки при бесконечно малом увеличении соответствующего аргумента.
Операторы момента импульса
 ,
,
 ,
,
 ,
,
 ,
,
 . (7.2)
. (7.2)
Формулы переходят друг в друга при циклической перестановке
 .
.
Сферические координаты

 ,
,  ,
,  . (7.3)
. (7.3)

Оператор градиента
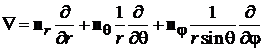 , (П.8.1)
, (П.8.1)
 – единичные орты. Операторы момента импульса
– единичные орты. Операторы момента импульса
 , (7.4)
, (7.4)
 . (7.5)
. (7.5)
Оператор Лапласа
Выражается через квадрат момента импульса
 , (7.6)
, (7.6)
определяет кинетическую энергию частицы.
Радиальная часть оператора Лапласа
 . (7.7)
. (7.7)
Перестановочное соотношение операторов (коммутатор)
 .
.
Предполагается, что правее каждого слагаемого находится функция, на которую действуют операторы:
 .
.
Выполняются
 ,
,
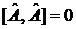 .
.
Если операторы коммутируют, т. е. их можно переставлять  , то соответствующие им физические величины измеримы одновременно с неограниченной точностью. Если коммутатор операторов не равен нулю, то чем точнее измеряется одна величина, тем больше неустранимая погрешность другой величины.
, то соответствующие им физические величины измеримы одновременно с неограниченной точностью. Если коммутатор операторов не равен нулю, то чем точнее измеряется одна величина, тем больше неустранимая погрешность другой величины.
Для операторов момента импульса
 ,
,
 ,
,
 ,
,
 . (7.8)
. (7.8)
Определенные значения имеют одновременно квадрат модуля момента импульса  и одна из его проекций
и одна из его проекций  .
.



 ,
, ;
;  ;
;  ;
; 
 .
. , для проекции возможны положительные и отрицательные значения.
, для проекции возможны положительные и отрицательные значения. образует полный ортонормированный базис на единичной сфере.
образует полный ортонормированный базис на единичной сфере. ,
, – радиус-вектор частицы,
– радиус-вектор частицы,  – импульс. Направление L определяется правилом правого винта.
– импульс. Направление L определяется правилом правого винта.
 ,
, ,
, ,
, .
. .
. ,
, 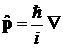 ,
, .
. , (7.1)
, (7.1) ,
, ,
, ,
, ,
, . (7.2)
. (7.2)
 ,
,  ,
,  . (7.3)
. (7.3)
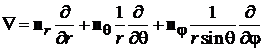 , (П.8.1)
, (П.8.1) – единичные орты. Операторы момента импульса
– единичные орты. Операторы момента импульса , (7.4)
, (7.4) . (7.5)
. (7.5) , (7.6)
, (7.6) . (7.7)
. (7.7) .
. .
. ,
,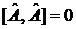 .
. , то соответствующие им физические величины измеримы одновременно с неограниченной точностью. Если коммутатор операторов не равен нулю, то чем точнее измеряется одна величина, тем больше неустранимая погрешность другой величины.
, то соответствующие им физические величины измеримы одновременно с неограниченной точностью. Если коммутатор операторов не равен нулю, то чем точнее измеряется одна величина, тем больше неустранимая погрешность другой величины. ,
, ,
, ,
, . (7.8)
. (7.8) и одна из его проекций
и одна из его проекций  .
. ,
, . (7.9)
. (7.9) изменяют на единицу число m, т. е. проекцию вектора момента импульса на ось z.
изменяют на единицу число m, т. е. проекцию вектора момента импульса на ось z. ,
, , (7.11)
, (7.11) . (7.12)
. (7.12)
 ,
, , (7.13)
, (7.13)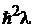 – собственное значение оператора
– собственное значение оператора 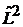 . Если объект находится в состоянии
. Если объект находится в состоянии  , то квадрат момента импульса равен
, то квадрат момента импульса равен  .
. . (7.14)
. (7.14) и собственное значение λ.
и собственное значение λ. .
. , и группируем слагаемые по их аргументам
, и группируем слагаемые по их аргументам .
. , (7.15)
, (7.15) . (7.16)
. (7.16) .
.
 .
. ,
, ,
,  ,
, – магнитное число,
– магнитное число, .
. ,
, ,
, . (7.17)
. (7.17) (1.43)
(1.43) . (7.18)
. (7.18) ,
, . (7.19)
. (7.19)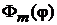 и
и  . В состоянии, описываемом функцией
. В состоянии, описываемом функцией 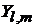 , измерение проекции момента импульса на ось z дает
, измерение проекции момента импульса на ось z дает .
.
 (7.11)
(7.11) .
. , т. е.
, т. е.  – повышающий оператор,
– повышающий оператор,  – понижающий оператор.
– понижающий оператор.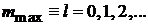 ,
,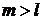 , тогда действие повышающего оператора на состояние с максимальной проекцией
, тогда действие повышающего оператора на состояние с максимальной проекцией .
. оператором
оператором . (7.12)
. (7.12) (7.19)
(7.19) , (7.13)
, (7.13)
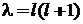 .
. ,
, , (7.20)
, (7.20) – модуль орбитального момента.
– модуль орбитального момента. , (7.24)
, (7.24)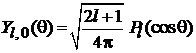 . (7.24а)
. (7.24а) (6.120)
(6.120)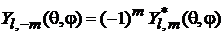 . (7.25)
. (7.25) , (6.123)
, (6.123) . (7.27)
. (7.27) ,
,
 ,
, ,
, ,
,  ,
,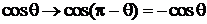 ,
, ,
, . (7.28)
. (7.28) ,
,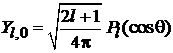 ,
, ,
, ,
, ,
,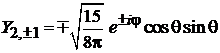 ,
, . (7.29)
. (7.29)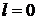 нет зависимости от углов – центрально-симметричное распределение;
нет зависимости от углов – центрально-симметричное распределение; нет зависимости от угла φ – осесимметричное распределение.
нет зависимости от угла φ – осесимметричное распределение. . (6.127)
. (6.127) ,
, . (7.32)
. (7.32) , тогда
, тогда .
.

 . (7.33)
. (7.33) , комплексно сопрягаем, используем
, комплексно сопрягаем, используем , (7.25)
, (7.25) ,
,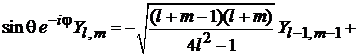
 . (7.34)
. (7.34) ,
,  ,
,  ,
,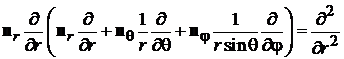 .
. ,
,  ,
,  ,
, .
.

 ,
,  ,
,  ,
, .
. . (П.8.3)
. (П.8.3)


