Формулы площадей некоторых плоских фигур
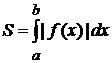 , (2.1)
, (2.1)
где  -- площадь криволинейной трапеции, ограниченной графиком функции
-- площадь криволинейной трапеции, ограниченной графиком функции  , отрезком
, отрезком  на оси ОХ и прямыми
на оси ОХ и прямыми  .
.
 , (2.2)
, (2.2)
где  -- площадь фигуры, заключенной между графиками функций
-- площадь фигуры, заключенной между графиками функций  и
и  ,
,  , прямыми
, прямыми  .
.
 , (2.3)
, (2.3)
где  -- площадь криволинейной трапеции, верхняя граница которой задана параметрическими уравнениями
-- площадь криволинейной трапеции, верхняя граница которой задана параметрическими уравнениями  непрерывны на
непрерывны на  , функция
, функция  монотонна на
монотонна на  .
.
 , (2.4)
, (2.4)
где  -- площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением
-- площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением  -- непрерывна на
-- непрерывна на  ), и двумя полярными радиусами, составляющими с полярной осью углы
), и двумя полярными радиусами, составляющими с полярной осью углы 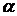 и
и  .
.
Пример 2.7. Найти площадь фигуры, ограниченной параболой  , прямой
, прямой  и осью ОХ.
и осью ОХ.
Прежде всего следует начертить эскиз данной плоской фигуры.
Часть фигуры находится над осью ОХ, а
часть—под осью ОХ. Следовательно, учитывая формулу (2.1), находим искомую площадь:


 .
.
Пример 2.8. Найти площадь фигуры, ограниченной прямой и параболой  .
.
В данном случае заштрихованная фигура
ограничена двумя линиями. Следователь
но, для вычисления площади этой фигуры
надо применить формулу (2.2). Для этого
найдем точки пересечения параболы и
прямой. Решая систему  ,
,
получим  . Тогда, согласно формуле (2.2), имеем:
. Тогда, согласно формуле (2.2), имеем:
 .
.
Пример 2.9. Вычислить площадь эллипса  .
.
Ввиду симметрии кривой относительно осей координат достаточно вычислить площадь части эллипса, находящегося в первой четверти. Поэтому находим
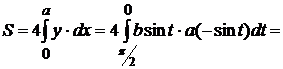
 .
.
Пример 2.10. Вычислить площадь фигуры ограниченной лемнискатой
 .
.
Предварительно остановимся на описании формы кривой. При  полярный радиус кривой
полярный радиус кривой  , следовательно, кривая проходит через полюс. Из уравнения кривой видно, что
, следовательно, кривая проходит через полюс. Из уравнения кривой видно, что 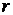 принимает действительные значения, когда
принимает действительные значения, когда  , то есть когда угол
, то есть когда угол  удовлетворяет неравенствам
удовлетворяет неравенствам  . Откуда
. Откуда  ,
,  . Заметим, что когда
. Заметим, что когда  , то полярный радиус
, то полярный радиус 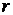 описывает часть кривой, расположенной в первой и четвертой четвертях, а при
описывает часть кривой, расположенной в первой и четвертой четвертях, а при 
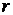 описывает часть кривой, расположенной во второй и третьей четвертях. Если к тому же учесть, что период
описывает часть кривой, расположенной во второй и третьей четвертях. Если к тому же учесть, что период  равен
равен  , то при замене
, то при замене  на
на 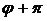 полярный радиус не изменяется. Таким образом, эта кривая расположена в двух вертикальных углах между прямыми, проведенными под углами
полярный радиус не изменяется. Таким образом, эта кривая расположена в двух вертикальных углах между прямыми, проведенными под углами  и
и  к полярной оси, и пересекает себя сама в полюсе О. Этих соображений уже достаточно для того, чтобы построить всю кривую.
к полярной оси, и пересекает себя сама в полюсе О. Этих соображений уже достаточно для того, чтобы построить всю кривую.
Учитывая симметрию кривой относительно полюса и полярной оси, мы можем ограничиться вычислением площади фигуры, находящейся в первой четверти
 . Следовательно, вся площадь фигуры, согласно формуле (2.4) будет равна:
. Следовательно, вся площадь фигуры, согласно формуле (2.4) будет равна:
 .
.
Пример 2.11. Найти площадь фигуры, ограниченной кардиоидой 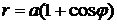 .
.
Так как кривая симметрична относительно полярной оси, в силу четности  , то достаточно вычислить площадь верхней половины
, то достаточно вычислить площадь верхней половины  . Тогда по формуле (2.4) находим:
. Тогда по формуле (2.4) находим:

 .
.
Упражнения
2.2. Найти площади фигур, ограниченных линиями:
1).  7).
7). 
2). 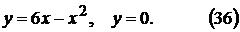 8).
8). 
3). 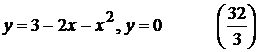 9).
9). 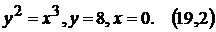
4).  10).
10). 
5).  11).
11). 
6).  12).
12). 
13). Осью ОХ и одной аркой циклоиды 
14). Астроидой 
15).  16).
16). 
17).  .
.
Формулы длин плоских кривых
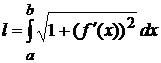 , (2.5)
, (2.5)
где  -- длина дуги кривой, заданной уравнением
-- длина дуги кривой, заданной уравнением  (функция
(функция  непрерывна на
непрерывна на  вместе со своей производной).
вместе со своей производной).
 (2.6)
(2.6)
где  -- длина дуги кривой, заданной параметрическими уравнениями
-- длина дуги кривой, заданной параметрическими уравнениями  (функции
(функции  и
и 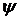 имеют непрерывные производные на
имеют непрерывные производные на  ,
,  ).
).
 (2.7)
(2.7)
где  -- длина дуги кривой, заданной в полярных координатах уравнением
-- длина дуги кривой, заданной в полярных координатах уравнением  (функция
(функция 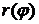 имеет непрерывную производную на
имеет непрерывную производную на  ).
).
Пример 2.12. Найти длину полукубической параболы 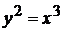 , отсеченной прямой
, отсеченной прямой  .
.
Данная кривая симметрична относительно оси ОХ. Мы вычислим длину дуги одной ветви кривой например, верхней) и результат удвоим. Из уравнения кривой  . Следовательно, по формуле (2.5) получим:
. Следовательно, по формуле (2.5) получим: 
 .
.
Пример 2.13. Найти длину дуги одной арки циклоиды  .
.
Циклоида --- плоская кривая, которую описывает точка М окружности радиуса  , катящейся без скольжения по оси ОХ из начала координат. Из уравнения циклоиды находим
, катящейся без скольжения по оси ОХ из начала координат. Из уравнения циклоиды находим 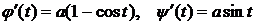 .
.
Когда 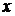 пробегает отрезок
пробегает отрезок  , параметр
, параметр  пробегает отрезок
пробегает отрезок  . Следовательно, по формуле (2.6) имеем:
. Следовательно, по формуле (2.6) имеем:
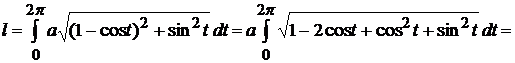
 .
.
Пример 2.14. Найти длину дуги кардиоиды 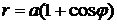 (см. рис. в примере 2.11).
(см. рис. в примере 2.11).
Так как кривая симметрична относительно полярной оси, то для 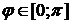 полярный радиус
полярный радиус 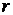 описывает половину кривой. Тогда, если учесть, что
описывает половину кривой. Тогда, если учесть, что  , формула (2.7) дает:
, формула (2.7) дает:

 .
.
Упражнения
Найти длину дуги кривой.
1). 
2). 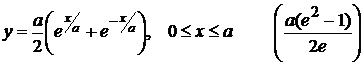
3). 
4). 
5). 
6). 
7). 
8). Астроиды 
9). 
10). Кардиоиды 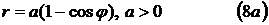 .
.
Формулы объемов тел вращения
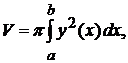 (2.8)
(2.8)
где 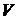 -- объем тела, полученного вращением криволинейной трапеции
-- объем тела, полученного вращением криволинейной трапеции 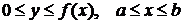 вокруг оси ОХ.
вокруг оси ОХ.
 (2.9)
(2.9)
где 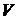 -- объем тела, полученного вращением криволинейной трапеции
-- объем тела, полученного вращением криволинейной трапеции  вокруг оси ОУ.
вокруг оси ОУ.
Пример 2.14. Найти объем тела, образованного вращением вокруг оси ОХ криволинейной трапеции, ограниченной линиями 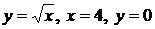 .
.
Изобразим тело вращения. По формуле (2.8) 
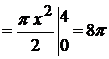 .
.
Пример 2.15. Найти объем тела, образованного вращением эллипса 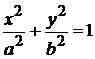 вокруг оси ОУ.
вокруг оси ОУ.
Так как эллипс симметричен относительно осей координат, то достаточно найти половину искомого объема и результат удвоить. По формуле (2.9) имеем
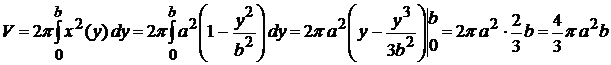
Упражнения
2.3. Найти объемы тел, образованных вращением фигуры, ограниченной линиями:
1).  вокруг: а) оси ОХ; б) оси ОУ.
вокруг: а) оси ОХ; б) оси ОУ. 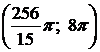 .
.
2). 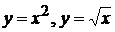 вокруг оси ОХ.
вокруг оси ОХ. 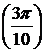
3). 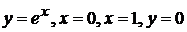 вокруг: а) оси ОХ; б) оси ОУ.
вокруг: а) оси ОХ; б) оси ОУ. 
4).  вокруг: а) оси ОХ; б) оси ОУ.
вокруг: а) оси ОХ; б) оси ОУ. 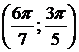
5). 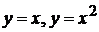 вокруг: а) оси ОХ; б) оси ОУ.
вокруг: а) оси ОХ; б) оси ОУ. 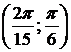
6). 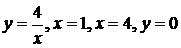 вокруг: а) оси ОХ; б) оси ОУ.
вокруг: а) оси ОХ; б) оси ОУ. 
7).  вокруг: а) оси ОХ; б) оси ОУ.
вокруг: а) оси ОХ; б) оси ОУ. 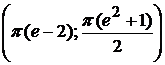 .
.
Эскизы графиков некоторых кривых (для справок).
3 Несобственные интегралы
Несобственные интегралы с бесконечными пределами интегрирования (несобственные интегралы первого рода)
Пусть функция  непрерывна на промежутке
непрерывна на промежутке 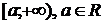 , тогда она непрерывна на любом промежутке
, тогда она непрерывна на любом промежутке  и существует
и существует 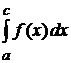 .
.
Определение 3.1. Если существует конечный предел 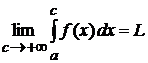 , то говорят, что функция
, то говорят, что функция  интегрируема на
интегрируема на  в несобственном смысле, величину
в несобственном смысле, величину 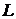 обозначают символом
обозначают символом 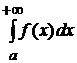 и называют сходящимся несобственным интегралом первого рода.
и называют сходящимся несобственным интегралом первого рода.
В противном случае говорят, что несобственный интеграл первого рода расходится.
Аналогично,  ;
;  , где
, где  -- любое число.
-- любое число.
Пример 3.1. Исследовать сходимость  .
.
По определению имеем 
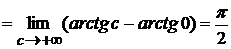 ,
,
то есть несобственный интеграл первого рода сходится и равен 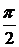 .
.
Пример 3.2. Исследовать сходимость  .
.
1) Если  , то
, то  2) Если
2) Если  , то
, то 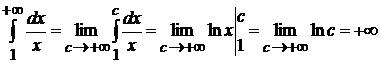 .
.
Таким образом, данный интеграл сходится при  и расходится при
и расходится при 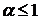 .
.
Несобственные интегралы от неограниченных функций (несобственные интегралы второго рода)
Пусть функция  непрерывна на промежутке
непрерывна на промежутке 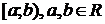 и не ограничена слева от точки
и не ограничена слева от точки 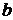 (ее называют особой точкой). Очевидно, что функция
(ее называют особой точкой). Очевидно, что функция  непрерывна на любом промежутке
непрерывна на любом промежутке 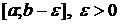 , заключенном в
, заключенном в  .
.
Определение 3.2. Если существует конечный предел 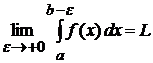 , то говорят, что функция
, то говорят, что функция  интегрируема на
интегрируема на  в несобственном смысле, величину
в несобственном смысле, величину 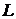 обозначают символом
обозначают символом 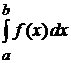 и называют сходящимся несобственным интегралом второго рода.
и называют сходящимся несобственным интегралом второго рода.
В противном случае говорят, что несобственный интеграл второго рода расходится.
Аналогично, если  -- особая точка, то, по определению,
-- особая точка, то, по определению, 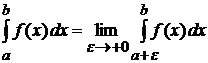 . Если внутренняя точка
. Если внутренняя точка  -- точка
-- точка  -- особая, то
-- особая, то 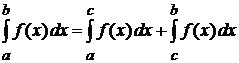 . Наконец, если
. Наконец, если  и
и 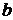 -- особые точки, то несобственный интеграл определяется как сумма:
-- особые точки, то несобственный интеграл определяется как сумма: 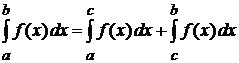 , где
, где  -- любая точка из
-- любая точка из  .
.
Пример 3.3. Исследовать сходимость  .
.
Точка  -- особая для подынтегральной функции
-- особая для подынтегральной функции 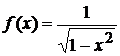 , она не ограничена в окрестности
, она не ограничена в окрестности  . На любом отрезке
. На любом отрезке 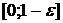 функция непрерывна, поэтому, по определению, имеем
функция непрерывна, поэтому, по определению, имеем  .
.
Следовательно, интеграл сходится.
Пример 3.4. Исследовать сходимость 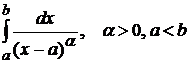 .
.
Подынтегральная функция не ограничена в окрестности точки  , поэтому точка
, поэтому точка  особая.
особая.
1) Пусть  . Тогда, по определению,
. Тогда, по определению, 

2) Если  , то
, то 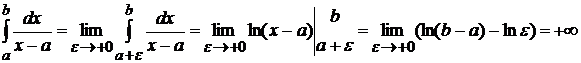 .
.
Таким образом, данный интеграл сходится при  и расходится при
и расходится при  .
.



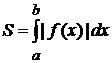 , (2.1)
, (2.1) -- площадь криволинейной трапеции, ограниченной графиком функции
-- площадь криволинейной трапеции, ограниченной графиком функции  , отрезком
, отрезком  на оси ОХ и прямыми
на оси ОХ и прямыми  .
. , (2.2)
, (2.2) и
и  ,
,  , прямыми
, прямыми  , (2.3)
, (2.3) непрерывны на
непрерывны на  , функция
, функция  монотонна на
монотонна на  , (2.4)
, (2.4) -- непрерывна на
-- непрерывна на 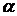 и
и  .
. , прямой
, прямой  и осью ОХ.
и осью ОХ.

 .
. .
. ,
, . Тогда, согласно формуле (2.2), имеем:
. Тогда, согласно формуле (2.2), имеем: .
. .
.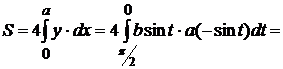
 .
. .
. полярный радиус кривой
полярный радиус кривой  , следовательно, кривая проходит через полюс. Из уравнения кривой видно, что
, следовательно, кривая проходит через полюс. Из уравнения кривой видно, что 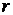 принимает действительные значения, когда
принимает действительные значения, когда  , то есть когда угол
, то есть когда угол  удовлетворяет неравенствам
удовлетворяет неравенствам  . Откуда
. Откуда  ,
,  . Заметим, что когда
. Заметим, что когда  равен
равен  , то при замене
, то при замене  на
на 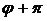 полярный радиус не изменяется. Таким образом, эта кривая расположена в двух вертикальных углах между прямыми, проведенными под углами
полярный радиус не изменяется. Таким образом, эта кривая расположена в двух вертикальных углах между прямыми, проведенными под углами  к полярной оси, и пересекает себя сама в полюсе О. Этих соображений уже достаточно для того, чтобы построить всю кривую.
к полярной оси, и пересекает себя сама в полюсе О. Этих соображений уже достаточно для того, чтобы построить всю кривую. . Следовательно, вся площадь фигуры, согласно формуле (2.4) будет равна:
. Следовательно, вся площадь фигуры, согласно формуле (2.4) будет равна: .
.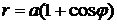 .
. , то достаточно вычислить площадь верхней половины
, то достаточно вычислить площадь верхней половины  . Тогда по формуле (2.4) находим:
. Тогда по формуле (2.4) находим:
 .
. 7).
7). 
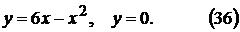 8).
8). 
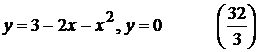 9).
9). 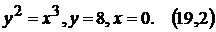
 10).
10). 
 11).
11). 
 12).
12). 


 16).
16). 
 .
.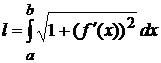 , (2.5)
, (2.5) -- длина дуги кривой, заданной уравнением
-- длина дуги кривой, заданной уравнением  (функция
(функция  (2.6)
(2.6) (функции
(функции 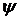 имеют непрерывные производные на
имеют непрерывные производные на  ,
,  ).
). (2.7)
(2.7) (функция
(функция 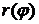 имеет непрерывную производную на
имеет непрерывную производную на 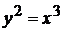 , отсеченной прямой
, отсеченной прямой  .
. . Следовательно, по формуле (2.5) получим:
. Следовательно, по формуле (2.5) получим: 
 .
. .
. , катящейся без скольжения по оси ОХ из начала координат. Из уравнения циклоиды находим
, катящейся без скольжения по оси ОХ из начала координат. Из уравнения циклоиды находим 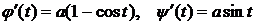 .
.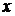 пробегает отрезок
пробегает отрезок  , параметр
, параметр  пробегает отрезок
пробегает отрезок  . Следовательно, по формуле (2.6) имеем:
. Следовательно, по формуле (2.6) имеем: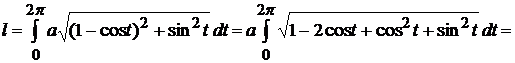
 .
.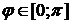 полярный радиус
полярный радиус  , формула (2.7) дает:
, формула (2.7) дает:
 .
.
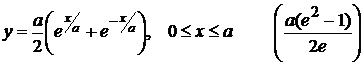







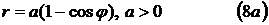 .
.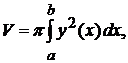 (2.8)
(2.8)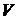 -- объем тела, полученного вращением криволинейной трапеции
-- объем тела, полученного вращением криволинейной трапеции 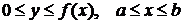 вокруг оси ОХ.
вокруг оси ОХ. (2.9)
(2.9) вокруг оси ОУ.
вокруг оси ОУ.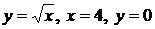 .
.
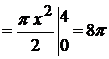 .
.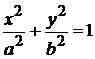 вокруг оси ОУ.
вокруг оси ОУ.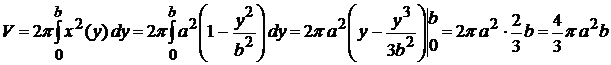
 вокруг: а) оси ОХ; б) оси ОУ.
вокруг: а) оси ОХ; б) оси ОУ. 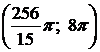 .
.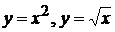 вокруг оси ОХ.
вокруг оси ОХ. 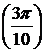
 вокруг: а) оси ОХ; б) оси ОУ.
вокруг: а) оси ОХ; б) оси ОУ. 
 вокруг: а) оси ОХ; б) оси ОУ.
вокруг: а) оси ОХ; б) оси ОУ. 
 вокруг: а) оси ОХ; б) оси ОУ.
вокруг: а) оси ОХ; б) оси ОУ. 
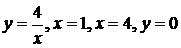 вокруг: а) оси ОХ; б) оси ОУ.
вокруг: а) оси ОХ; б) оси ОУ. 
 вокруг: а) оси ОХ; б) оси ОУ.
вокруг: а) оси ОХ; б) оси ОУ. 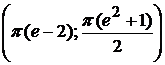 .
. непрерывна на промежутке
непрерывна на промежутке 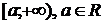 , тогда она непрерывна на любом промежутке
, тогда она непрерывна на любом промежутке  и существует
и существует 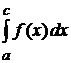 .
.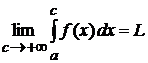 , то говорят, что функция
, то говорят, что функция  в несобственном смысле, величину
в несобственном смысле, величину 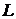 обозначают символом
обозначают символом 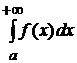 и называют сходящимся несобственным интегралом первого рода.
и называют сходящимся несобственным интегралом первого рода. ;
;  , где
, где  -- любое число.
-- любое число. .
.
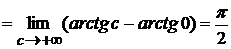 ,
,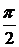 .
. .
. , то
, то  2) Если
2) Если  , то
, то 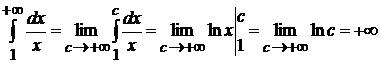 .
. и расходится при
и расходится при 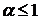 .
.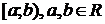 и не ограничена слева от точки
и не ограничена слева от точки 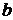 (ее называют особой точкой). Очевидно, что функция
(ее называют особой точкой). Очевидно, что функция 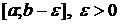 , заключенном в
, заключенном в  .
.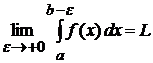 , то говорят, что функция
, то говорят, что функция 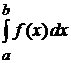 и называют сходящимся несобственным интегралом второго рода.
и называют сходящимся несобственным интегралом второго рода. -- особая точка, то, по определению,
-- особая точка, то, по определению, 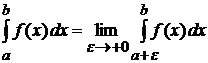 . Если внутренняя точка
. Если внутренняя точка  -- особая, то
-- особая, то 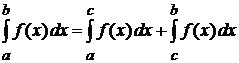 . Наконец, если
. Наконец, если  .
. .
. -- особая для подынтегральной функции
-- особая для подынтегральной функции 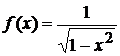 , она не ограничена в окрестности
, она не ограничена в окрестности 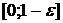 функция непрерывна, поэтому, по определению, имеем
функция непрерывна, поэтому, по определению, имеем  .
.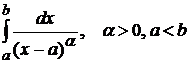 .
.

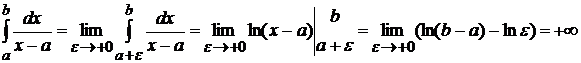 .
. и расходится при
и расходится при  .
.


