Если подынтегральная функция непрерывна и неотрицательна на 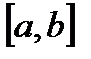 , то
, то  есть масса неоднородного стержня
есть масса неоднородного стержня 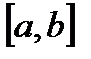 с плотностью
с плотностью  .
.
5.3. Теорема существования определенного интеграла.
Если  непрерывна на отрезке
непрерывна на отрезке 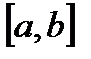 , то
, то 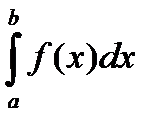 существует.
существует.
5.4. Свойства определенного интеграла.
1) 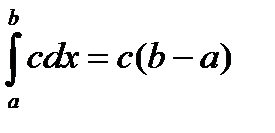
2) 
3) Постоянный множитель можно выносить за знак интеграла.
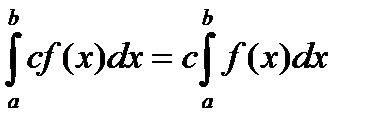 , с=const.
, с=const.
4) 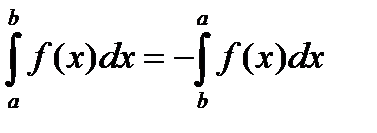
5) 
6) 
7) Если  знакопостоянна на
знакопостоянна на 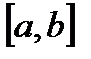 , то
, то  имеет тот же знак, что и
имеет тот же знак, что и  .
.
8) Если  ,
,  , то
, то  .
.
9) Теорема об оценке интеграла.
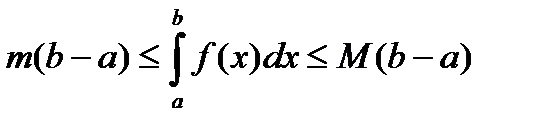 , где m и M – соответственно наименьшее и наибольшее значения
, где m и M – соответственно наименьшее и наибольшее значения  на
на 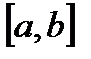 .
.
Замечание: свойства 2, 3, 4, 5, 7, 8, 9 справедливы, если соответствующие интегралы существуют.
10) Теорема о среднем.
Если  непрерывна на
непрерывна на 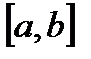 , то существует точка
, то существует точка  , для которой справедливо равенство
, для которой справедливо равенство 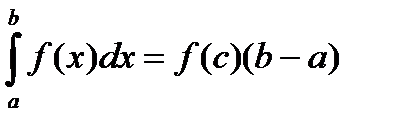 .
.
Доказательство.
Так как  непрерывна на отрезке
непрерывна на отрезке 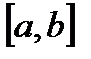 , то она на этом отрезке достигает свои наименьшее и наибольшее значения и принимает все промежуточные значения между наименьшим и наибольшим значениями.
, то она на этом отрезке достигает свои наименьшее и наибольшее значения и принимает все промежуточные значения между наименьшим и наибольшим значениями.
 , тогда по теореме об оценке интеграла имеем:
, тогда по теореме об оценке интеграла имеем:
 , т.к. по условию
, т.к. по условию  и
и  существует.
существует.
В последних неравенствах все части неравенств поделим на (b-a), в результате получим:
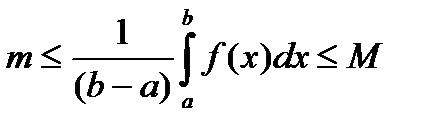 .
.
Т.к.  принимает все промежуточные значения между m и M, то
принимает все промежуточные значения между m и M, то 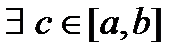 , в которой
, в которой 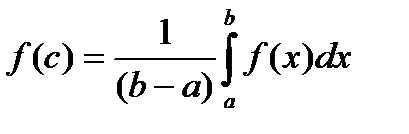 . Теорема доказана.
. Теорема доказана.
Выражение 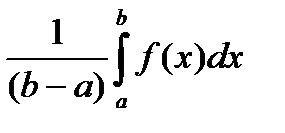 называется средним значением функции
называется средним значением функции  на
на 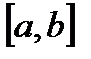 .
.
Лекция 6.
Тема: Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница. Интегрирование по частям и заменой переменной в определенном интеграле.
6.1. Интеграл с переменным верхним пределом.
Пусть  непрерывная функция на отрезке
непрерывная функция на отрезке 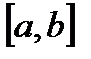 . Рассмотрим интеграл
. Рассмотрим интеграл  , где верхний предел
, где верхний предел 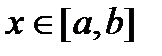 . Верхний предел x и x под знаком интеграла разные и имеют разный смысл. Верхний предел x является произвольной фиксированной точкой отрезка
. Верхний предел x и x под знаком интеграла разные и имеют разный смысл. Верхний предел x является произвольной фиксированной точкой отрезка 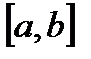 , а x под знаком интеграла является переменной, которая изменяется от a до верхнего предела x. Интеграл
, а x под знаком интеграла является переменной, которая изменяется от a до верхнего предела x. Интеграл  называется интегралом с переменным верхним пределом, т.к. верхний предел x может принимать любое значение из отрезка
называется интегралом с переменным верхним пределом, т.к. верхний предел x может принимать любое значение из отрезка 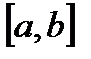 . По условию
. По условию  непрерывна на любом отрезке
непрерывна на любом отрезке 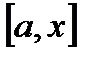 ,
, 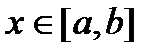 , то по теореме существования интеграл
, то по теореме существования интеграл  существует для любого
существует для любого 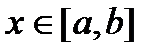 , поэтому
, поэтому 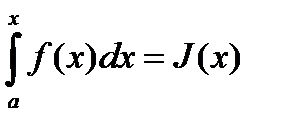 является функцией от x.
является функцией от x.
Далее покажем, что функция  является дифференцируемой функцией.
является дифференцируемой функцией.
Теорема. Если  непрерывна на отрезке
непрерывна на отрезке 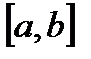 , то производная от интеграла с переменным верхним пределом равна подынтегральной функции, т.е.
, то производная от интеграла с переменным верхним пределом равна подынтегральной функции, т.е.  является первообразной для подынтегральной функции на
является первообразной для подынтегральной функции на 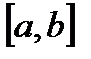 ,
, 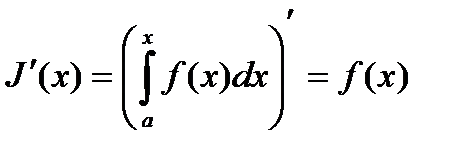
Доказательство.
По определению производной 

где с расположено между 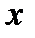 и
и  .
.
Последнее равенство имеет место в силу теоремы о среднем. Подставляя вместо  полученное выражение, будем иметь
полученное выражение, будем иметь
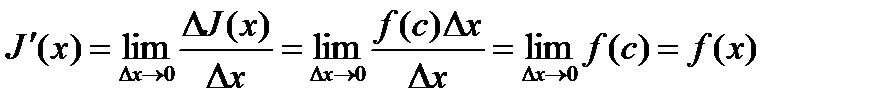 .
.
Точка с расположена между 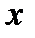 и
и  , поэтому
, поэтому  при
при  . Так как
. Так как  непрерывна в точке x, то
непрерывна в точке x, то  . ▼
. ▼
6.2. Формула Ньютона-Лейбница.
Теорема. Справедлива формула  , где Ф(x) какая-либо первообразная для подынтегральной функции
, где Ф(x) какая-либо первообразная для подынтегральной функции  .
.
Доказательство.
Рассмотрим интеграл с переменным верхним пределом  . Этот интеграл является первообразной для функции
. Этот интеграл является первообразной для функции  . Пусть
. Пусть  – произвольная другая первообразная для
– произвольная другая первообразная для  . Две различные первообразные для функции
. Две различные первообразные для функции  различаются на константу. Поэтому
различаются на константу. Поэтому  . Положим верхний предел
. Положим верхний предел  , тогда получим:
, тогда получим:  , отсюда
, отсюда 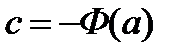 ,
, 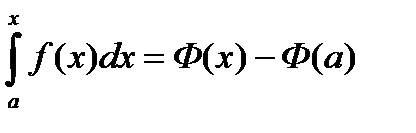 . В последнем интеграле вместо верхнего предела x подставим
. В последнем интеграле вместо верхнего предела x подставим 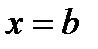 , тогда получим:
, тогда получим:  . ▼
. ▼
Пример. Вычислить 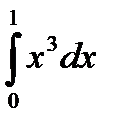
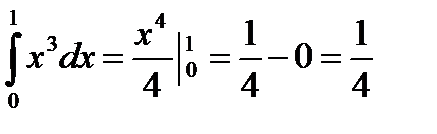
6.3. Интегрирование по частям в определенном интеграле.
Теорема. Справедлива формула  .
.
Доказательство. Имеем: 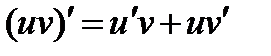 .
.
Почленно проинтегрируем последнее равенство

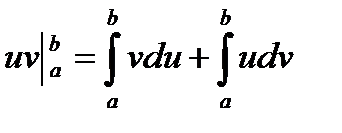
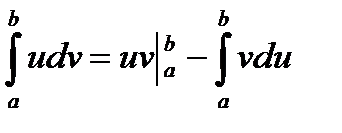 . ▼
. ▼
Пример. Вычислить 
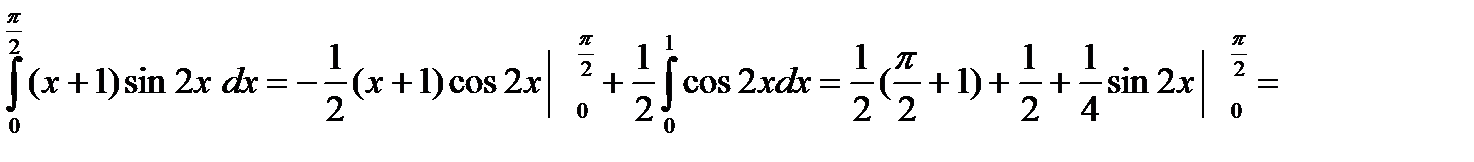
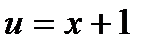



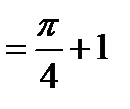 .
.
Пример. Вычислить 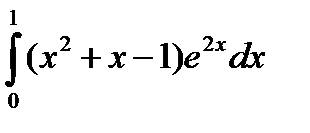

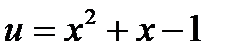 ;
; 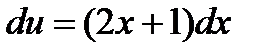
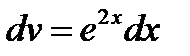 ;
; 
К последнему интегралу применим еще раз формулу интегрирование по частям.

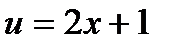 ;
; 
 ;
; 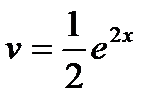

Пример. Вычислить 

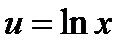 ;
; 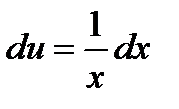
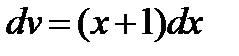 ;
; 

6.4. Замена переменной в определенном интеграле.
Пусть 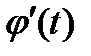 непрерывна на отрезке
непрерывна на отрезке 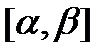 и
и 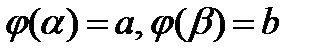 , а функция
, а функция  непрерывна на отрезке
непрерывна на отрезке 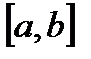 .
.
Справедлива формула
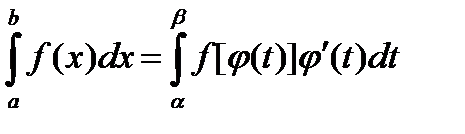 .
.
Доказательство. Так как  непрерывна на
непрерывна на 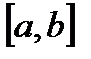 , то она на этом отрезке имеет первообразную, которую обозначим
, то она на этом отрезке имеет первообразную, которую обозначим 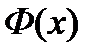 .
.
Функция 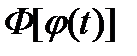 является первообразной для функции
является первообразной для функции 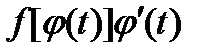 на отрезке
на отрезке 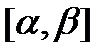 .
.
В самом деле, применяя правило дифференцирования сложной функции, получим:  , где
, где  .
.
Используя формулу Ньютона-Лейбница, получим:  . ▼
. ▼
Пример. Вычислить 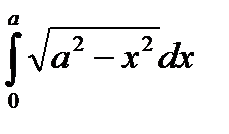
Сделаем замену 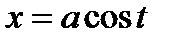

Если 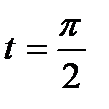 , то
, то 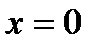 , если
, если  , то
, то 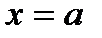
Следовательно, 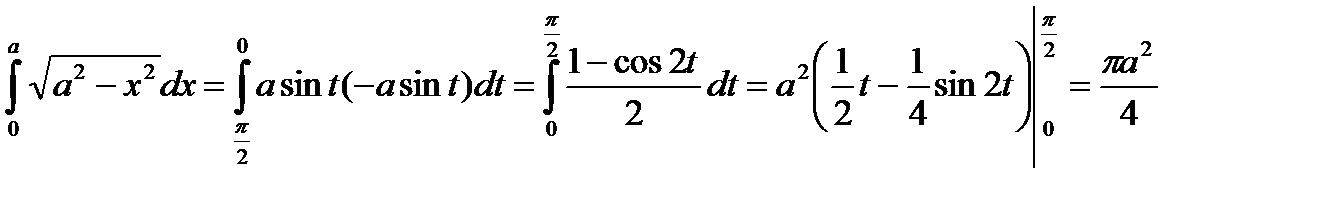
Лекция 7.
Тема: Интегрирование четных и нечетных функций. Несобственные интегралы.
7.1. Интегрирование четных и нечетных функций.
Пусть  - четная функция на отрезке
- четная функция на отрезке 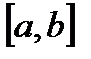 , т.е.
, т.е. 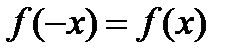 . Рассмотрим интеграл
. Рассмотрим интеграл

В интеграле 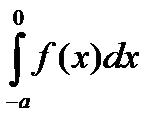 сделаем замену переменной
сделаем замену переменной  .
.

В результате получим
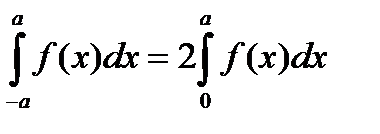
Пусть 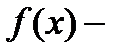 нечетная функция на отрезке
нечетная функция на отрезке 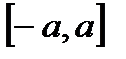 , т.е.
, т.е.  .
.
Как и в предыдущем случае в интеграле 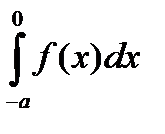 сделаем замену
сделаем замену  . В результате получим:
. В результате получим:  .
.
 .
.
7.2. Несобственные интегралы.
До сих пор мы рассматривали интегралы 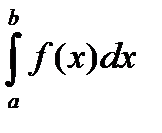 , для которых отрезок
, для которых отрезок 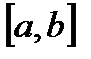 конечен и функция
конечен и функция  ограничена на отрезке
ограничена на отрезке 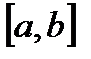 . При этом
. При этом 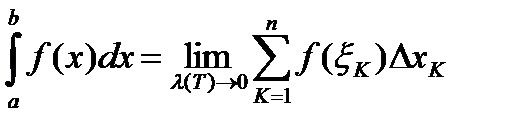 .
.
На практике часто встречаются случаи, когда 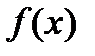 задана на бесконечном промежутке и непрерывна на нем либо
задана на бесконечном промежутке и непрерывна на нем либо 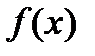 задана на конечном отрезке
задана на конечном отрезке 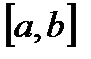 , но неограниченна на нем. Если промежуток
, но неограниченна на нем. Если промежуток 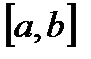 бесконечен, то при любом разбиении его на конечное число частей один из промежутков будет бесконечным, сумма
бесконечен, то при любом разбиении его на конечное число частей один из промежутков будет бесконечным, сумма  равна
равна 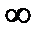 , а
, а 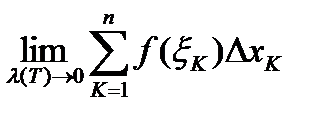 не существует. Если же
не существует. Если же 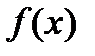 определена на конечном отрезке
определена на конечном отрезке 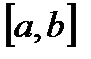 , но неограниченна, то всегда существует отрезок разбиения
, но неограниченна, то всегда существует отрезок разбиения 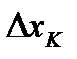 , на котором
, на котором 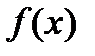 неограниченна и на этом отрезке можно выбрать точку
неограниченна и на этом отрезке можно выбрать точку 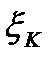 так, что
так, что  , где М наперед заданное число и в этом случае
, где М наперед заданное число и в этом случае 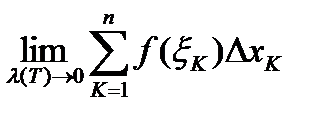 не существует.
не существует.
Если 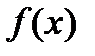 задана на бесконечном промежутке и непрерывна на нем либо
задана на бесконечном промежутке и непрерывна на нем либо 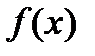 задана на конечном промежутке и неограниченна на нем, то интегралы от таких функций определяются с помощью предельного перехода и эти интегралы называются несобственными.
задана на конечном промежутке и неограниченна на нем, то интегралы от таких функций определяются с помощью предельного перехода и эти интегралы называются несобственными.
7.2.1. Несобственные интегралы от непрерывных функций по бесконечному промежутку.
Пусть 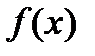 задана и непрерывна на промежутке
задана и непрерывна на промежутке 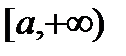 .
.
Рассмотрим интеграл  , этот интеграл существует
, этот интеграл существует  , т.к.
, т.к. 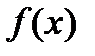 непрерывна на отрезке
непрерывна на отрезке 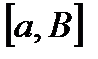 .
.
Положим по определению
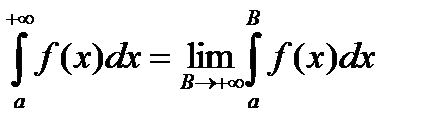 . (1)
. (1)
Интеграл 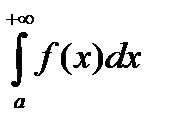 называется несобственным интегралом. Если предел в равенстве (1) существует, то говорят, что несобственный интеграл сходится. Если предел в равенстве (1) не существует, то говорят, что несобственный интеграл расходится.
называется несобственным интегралом. Если предел в равенстве (1) существует, то говорят, что несобственный интеграл сходится. Если предел в равенстве (1) не существует, то говорят, что несобственный интеграл расходится.
Пусть теперь функция 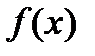 задана и непрерывна на промежутке
задана и непрерывна на промежутке 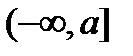 .
.
Несобственный интеграл  определяется аналогично:
определяется аналогично:

Далее, пусть функция 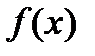 задана и непрерывна на всей числовой оси
задана и непрерывна на всей числовой оси 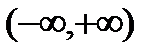 .
.
Несобственный интеграл  определяется следующим образом:
определяется следующим образом:
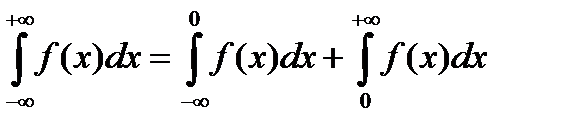 ,
,
при условии, что оба интеграла справа сходятся.
Заметим, что вместо 0 можно взять любое конечное число а и при этом сходимость несобственного интеграла 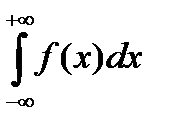 и его значение не изменится.
и его значение не изменится.



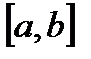 , то
, то  есть масса неоднородного стержня
есть масса неоднородного стержня  .
. непрерывна на отрезке
непрерывна на отрезке 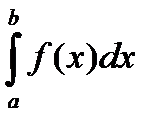 существует.
существует.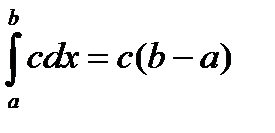

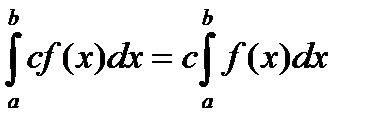 , с=const.
, с=const.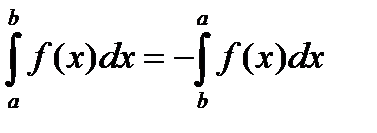


 имеет тот же знак, что и
имеет тот же знак, что и  ,
,  , то
, то  .
.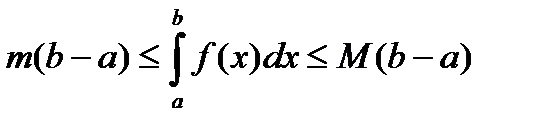 , где m и M – соответственно наименьшее и наибольшее значения
, где m и M – соответственно наименьшее и наибольшее значения  , для которой справедливо равенство
, для которой справедливо равенство 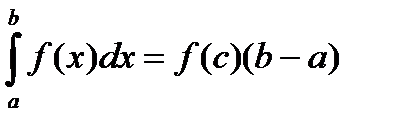 .
. , тогда по теореме об оценке интеграла имеем:
, тогда по теореме об оценке интеграла имеем: , т.к. по условию
, т.к. по условию  и
и 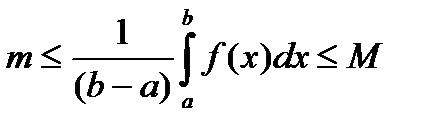 .
.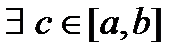 , в которой
, в которой 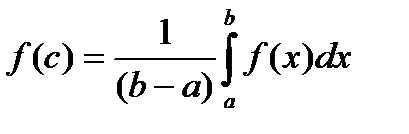 . Теорема доказана.
. Теорема доказана.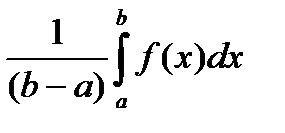 называется средним значением функции
называется средним значением функции  , где верхний предел
, где верхний предел 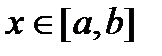 . Верхний предел x и x под знаком интеграла разные и имеют разный смысл. Верхний предел x является произвольной фиксированной точкой отрезка
. Верхний предел x и x под знаком интеграла разные и имеют разный смысл. Верхний предел x является произвольной фиксированной точкой отрезка 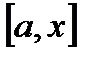 ,
, 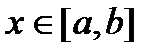 , то по теореме существования интеграл
, то по теореме существования интеграл 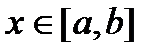 , поэтому
, поэтому 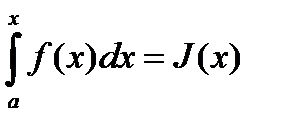 является функцией от x.
является функцией от x. является дифференцируемой функцией.
является дифференцируемой функцией. является первообразной для подынтегральной функции на
является первообразной для подынтегральной функции на 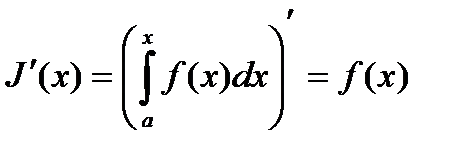


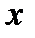 и
и  .
. полученное выражение, будем иметь
полученное выражение, будем иметь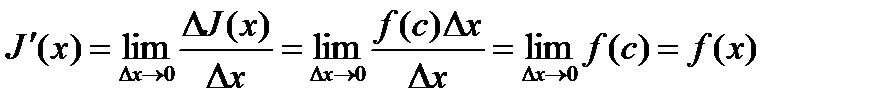 .
. при
при  . Так как
. Так как  . ▼
. ▼ , где Ф(x) какая-либо первообразная для подынтегральной функции
, где Ф(x) какая-либо первообразная для подынтегральной функции  . Этот интеграл является первообразной для функции
. Этот интеграл является первообразной для функции  – произвольная другая первообразная для
– произвольная другая первообразная для  . Положим верхний предел
. Положим верхний предел  , тогда получим:
, тогда получим:  , отсюда
, отсюда 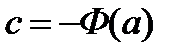 ,
, 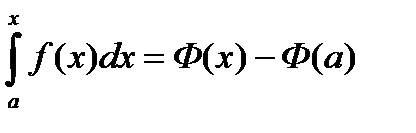 . В последнем интеграле вместо верхнего предела x подставим
. В последнем интеграле вместо верхнего предела x подставим 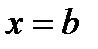 , тогда получим:
, тогда получим:  . ▼
. ▼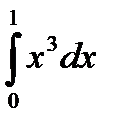
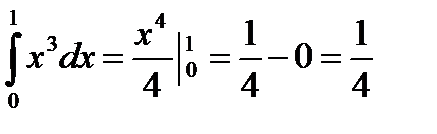
 .
.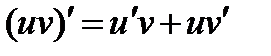 .
.
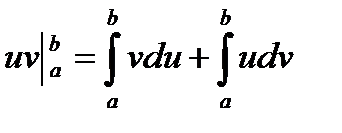
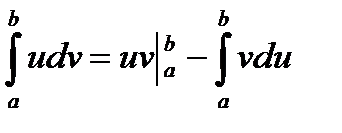 . ▼
. ▼
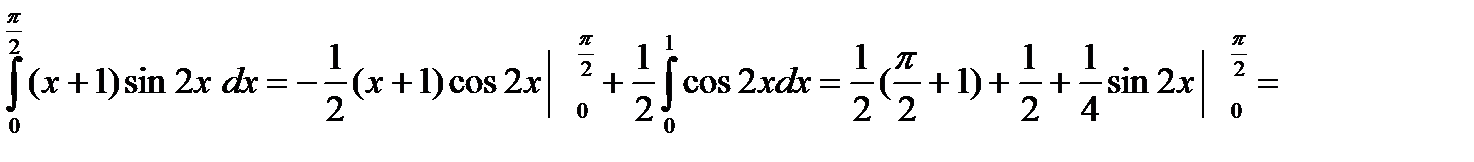
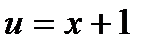



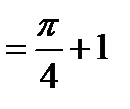 .
.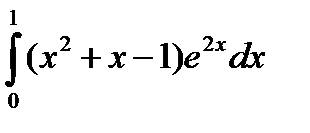

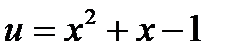 ;
; 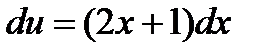
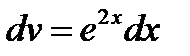 ;
; 

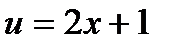 ;
; 
 ;
; 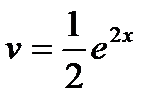



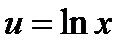 ;
; 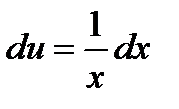
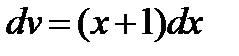 ;
; 

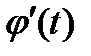 непрерывна на отрезке
непрерывна на отрезке 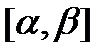 и
и 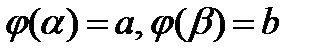 , а функция
, а функция 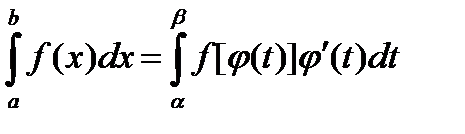 .
.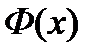 .
.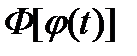 является первообразной для функции
является первообразной для функции 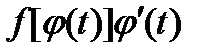 на отрезке
на отрезке  , где
, где  .
. . ▼
. ▼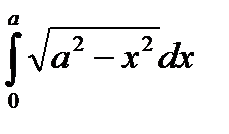
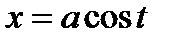

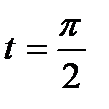 , то
, то 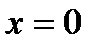 , если
, если  , то
, то 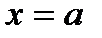
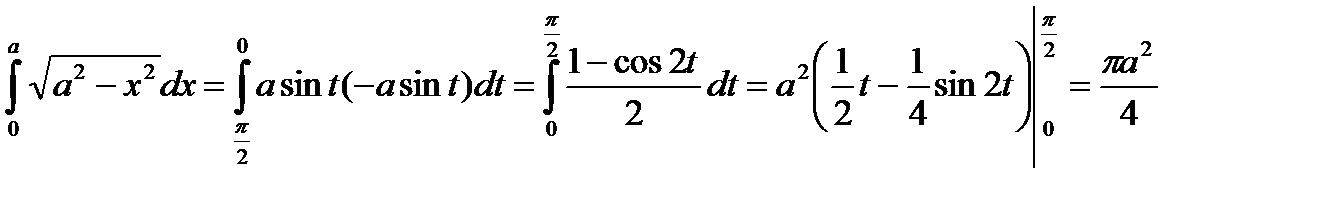
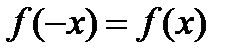 . Рассмотрим интеграл
. Рассмотрим интеграл
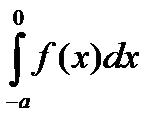 сделаем замену переменной
сделаем замену переменной  .
.
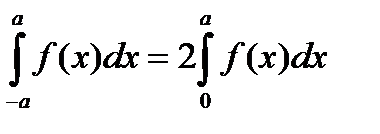
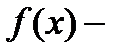 нечетная функция на отрезке
нечетная функция на отрезке 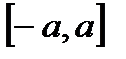 , т.е.
, т.е.  .
.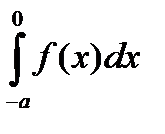 сделаем замену
сделаем замену  .
. .
.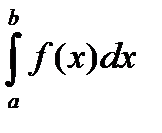 , для которых отрезок
, для которых отрезок 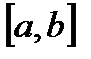 конечен и функция
конечен и функция  ограничена на отрезке
ограничена на отрезке 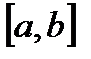 . При этом
. При этом 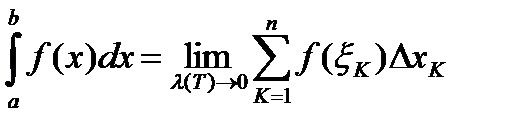 .
.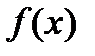 задана на бесконечном промежутке и непрерывна на нем либо
задана на бесконечном промежутке и непрерывна на нем либо 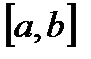 , но неограниченна на нем. Если промежуток
, но неограниченна на нем. Если промежуток  равна
равна 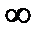 , а
, а 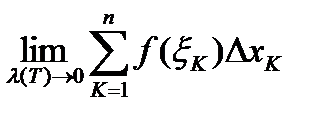 не существует. Если же
не существует. Если же 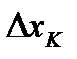 , на котором
, на котором 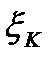 так, что
так, что  , где М наперед заданное число и в этом случае
, где М наперед заданное число и в этом случае 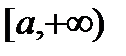 .
. , этот интеграл существует
, этот интеграл существует  , т.к.
, т.к. 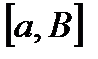 .
.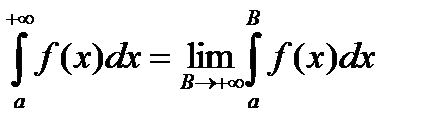 . (1)
. (1)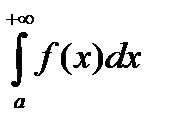 называется несобственным интегралом. Если предел в равенстве (1) существует, то говорят, что несобственный интеграл сходится. Если предел в равенстве (1) не существует, то говорят, что несобственный интеграл расходится.
называется несобственным интегралом. Если предел в равенстве (1) существует, то говорят, что несобственный интеграл сходится. Если предел в равенстве (1) не существует, то говорят, что несобственный интеграл расходится.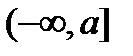 .
. определяется аналогично:
определяется аналогично:
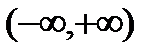 .
. определяется следующим образом:
определяется следующим образом: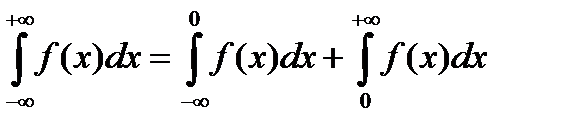 ,
,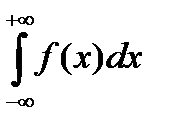 и его значение не изменится.
и его значение не изменится.


