Содержание.
| Лекция 1.Первообразная. Определение неопределенного интеграла, его свойства. Таблица интегралов. Замена переменной в неопределенном интеграле……………………………………………………………………………
Лекция 2.Интегрирование по частям. Замена переменной в неопределенном интеграле. Интегрирование рациональных дробей. Разложение правильной рациональной дроби на простейшие……………………………………………...
Лекция 3.Интегрирование простейших рациональных дробей. Интегрирование тригонометрических выражений………………………………
Лекция 4.Интегрирование некоторых иррациональных выражений. Примеры интегралов, не выражающихся в элементарных функциях………….
Лекция 5.Задачи, приводящие к понятию определенного интеграла. Определение определенного интеграла, его свойства. Теорема существования определенного интеграла………………………………………........................................................
Лекция 6.Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница. Интегрирование по частям и заменой переменной в определенном интеграле……………………………………………………………………………
Лекция 7.Интегрирование четных и нечетных функций. Несобственные интегралы…………………………………………………………………………...
Лекция 8. Вычисление площадей плоских фигур. Вычисление объемов тел…
Лекция 9.Вычисление длины кривой, площади поверхности тела вращения..
|
|
Введение. В первом семестре мы по известной функции находили ее производную. Теперь рассмотрим обратное действие, т.е. по известной производной найти саму функцию. Решение этой обратной задачи имеет важное значение в анализе и его приложениях. В частности, полученные результаты мы будем применять при вычислении определенных интегралов и решении дифуравнений.
Лекция 1.
Тема: Первообразная. Определение неопределенного интеграла, его свойства. Таблица интегралов. Замена переменной в неопределенном интеграле.
1.1. Первообразная
Определение. Первообразной для функции  в интервале
в интервале  называется функция
называется функция  , производная которой равна
, производная которой равна  , т.е.
, т.е.  .
.
Пример. Найти первообразную для функции  ,
,  , так как
, так как  . Легко заметить, что любая функция
. Легко заметить, что любая функция  является первообразной для функции
является первообразной для функции  , где
, где  – const.
– const.
Таким образом, если функция  имеет одну первообразную
имеет одну первообразную 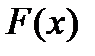 , то
, то  имеет бесконечно много первообразных
имеет бесконечно много первообразных  т.к.
т.к.  .
.
Теорема: Если функция  в интервале имеет первообразную
в интервале имеет первообразную  , то любая другая первообразная отличается от данной на константу.
, то любая другая первообразная отличается от данной на константу.
Доказательство: Пусть  и
и  – две первообразные для функции
– две первообразные для функции  в интервале
в интервале  , т.е.
, т.е.  и
и  . Рассмотрим функцию
. Рассмотрим функцию  .
.
Функция  дифференцируема в интервале
дифференцируема в интервале  как разность двух дифференцируемых функций. Следовательно,
как разность двух дифференцируемых функций. Следовательно,  непрерывна в интервале
непрерывна в интервале  . Рассмотрим произвольный отрезок
. Рассмотрим произвольный отрезок  принадлежащий
принадлежащий  . Функция
. Функция  непрерывна на отрезке
непрерывна на отрезке  , дифференцируема в интервале
, дифференцируема в интервале  . Следовательно,
. Следовательно,  на отрезке
на отрезке  удовлетворяет всем условиям теоремы Лагранжа, по которой выполняется равенство
удовлетворяет всем условиям теоремы Лагранжа, по которой выполняется равенство  , где
, где  некоторая точка интервала
некоторая точка интервала  .
.
Имеем  .Поэтому
.Поэтому  и
и  . Отсюда следует, что
. Отсюда следует, что  и
и  . ▼
. ▼
В дальнейшем будет доказано, что всякая непрерывная функция имеет первообразную.
1.2. Определение неопределенного интеграла и его свойства.
Определение: Неопределенным интегралом для функции  называют совокупность всех ее первообразных
называют совокупность всех ее первообразных  .
.
Неопределенный интеграл обозначается  .
.
 , где
, где  какая-либо одна из первообразных для
какая-либо одна из первообразных для  .
.  называется подынтегральной функцией,
называется подынтегральной функцией,  подынтегральным выражением.
подынтегральным выражением.
Свойства неопределенного интеграла:
1. 
Доказательство. Пусть  одна из первообразных функции
одна из первообразных функции  , тогда
, тогда 
 .
.
Таким образом, действие интегрирования проверяется дифференцированием.
2. 
Свойство 2 вытекает из свойства 1.
3. Постоянный множитель можно выносить за знак неопределенного интеграла.

4.  .
.
Таблица интегралов.
Из определения интеграла и формул дифференцирования функций следуют равенства:
1)  2)
2) 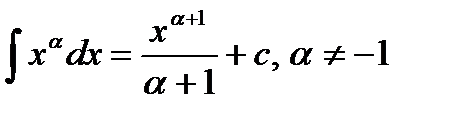 3)
3)  4)
4)  5)
5)  6)
6) 
| 7)  8)
8)  9)
9)  10)
10)  11)
11) 
|
Все формулы проверяются дифференцированием.
Так из равенства:

следует справедливость второй формулы.
Проверим теперь формулу 3 при  .
.
Имеем:  и
и  .
.
В последнем равенстве применили правило дифференцирования сложной функции.
1.3. Замена переменной в неопределенном интеграле.
Замена переменной в неопределенном интеграле есть действие обратное дифференцированию сложной функции.
Справедливо равенство:
 , где
, где  (1)
(1)
В самом деле, пусть  первообразная для
первообразная для  тогда
тогда

Использование формулы (1) слева направо называется подведением под знак дифференциала.
Приведем некоторые примеры:
Пример
 , где
, где 
В данном примере подводим под знак дифференциала 2х
Имеем:  отсюда
отсюда  .
.
Пример  , где
, где 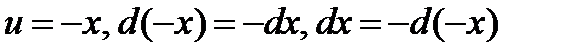
Пример


Пример
 , т.к.
, т.к. 
В дальнейшем мы покажем использование формулы (1) замены переменной справа налево.
Лекция 2.
Тема: Интегрирование по частям. Замена переменной в неопределенном интеграле. Интегрирование рациональных дробей. Разложение правильной рациональной дроби на простейшие.
2.1. Интегрирование по частям.
Интегрирование по частям есть действие обратное дифференцированию произведения.
Имеем: 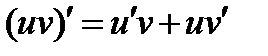
Проинтегрируем обе части равенства:

 отсюда получаем:
отсюда получаем:
Пример


Пример

В интеграле  еще раз применим интегрирование по частям:
еще раз применим интегрирование по частям:

В данном примере интегрирование по частям применено дважды.
Пример
 , где
, где 
Замечание: Если под знаком интеграла имеем дробь  , числитель которой есть производная знаменателя, то интеграл от этой дроби равен логарифму натуральному от модуля знаменателя!!!
, числитель которой есть производная знаменателя, то интеграл от этой дроби равен логарифму натуральному от модуля знаменателя!!!
Пример



2.2. Интегрирование заменой переменной.
Рассмотрим формулу (1) в следующем виде:
 , где
, где  обратная функция для функции
обратная функция для функции  . Обратим внимание на то, что при замене переменной
. Обратим внимание на то, что при замене переменной  последняя функция должна иметь обратную.
последняя функция должна иметь обратную.
В данном интеграле сделана замена  . Сложность заключается в том, что таких замен бесконечно много и нужно подобрать такую, чтобы вновь полученный интеграл был проще исходного.
. Сложность заключается в том, что таких замен бесконечно много и нужно подобрать такую, чтобы вновь полученный интеграл был проще исходного.
Пример


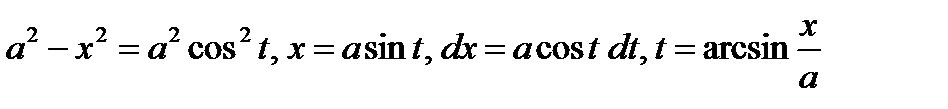

2.3. Интегрирование рациональных дробей. Разложение правильной дроби на простейшие.
Определение: Рациональной дробью называется отношение двух многочленов.
 , где
, где  и
и  многочлены соответственно степеней m и n.
многочлены соответственно степеней m и n.
Определение: Рациональная дробь  называется правильной, если степень числителя меньше степени знаменателя, т.е.
называется правильной, если степень числителя меньше степени знаменателя, т.е.  , в противном случае рациональная дробь – неправильная.
, в противном случае рациональная дробь – неправильная.
Всякая неправильная дробь всегда может быть представлена в виде суммы многочлена и правильной рациональной дроби. Это достигается делением числителя на знаменатель.
Отсюда следует, что интегрирование неправильной рациональной дроби всегда можно свести к интегрированию правильной рациональной дроби.
В дальнейшем мы покажем, что всякую правильную рациональную дробь можно представить в виде суммы простейших рациональных дробей.
К простейшим рациональным дробям относятся дроби:
1) 
2) 
3) 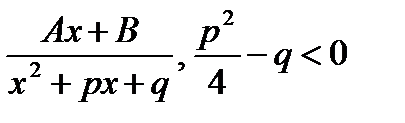
4) 
Пусть дана правильная рациональная дробь  .
.
Коэффициент при  у многочлена
у многочлена  можно считать равным 1. Этого можно достичь, деля числитель и знаменатель на одно и то же число.
можно считать равным 1. Этого можно достичь, деля числитель и знаменатель на одно и то же число.
Многочлен  имеет ровно n корней, учитывая их кратность, т.е.:
имеет ровно n корней, учитывая их кратность, т.е.:
 , где
, где  действительные корни,
действительные корни,  комплексные корни,
комплексные корни,  кратность соответствующих корней.
кратность соответствующих корней.
Так как  – многочлен с действительными коэффициентами, то каждому комплексному корню соответствует сопряженный комплексный корень той же кратности.
– многочлен с действительными коэффициентами, то каждому комплексному корню соответствует сопряженный комплексный корень той же кратности.
Пусть  комплексный корень
комплексный корень  кратности
кратности  , тогда
, тогда 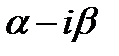 тоже корень
тоже корень  кратности
кратности  . Поэтому в многочлене
. Поэтому в многочлене  будет присутствовать произведение:
будет присутствовать произведение:

где 
Следовательно, многочлен  всегда можно представить в следующем виде:
всегда можно представить в следующем виде:
 .
.
Теорема: Всякую правильную рациональную дробь всегда можно представить в виде суммы простейших рациональных дробей в следующем виде:

где А, В, С с соответствующими индексами – неопределенные коэффициенты.
(теорема без доказательства)
Неопределенные коэффициенты находятся следующим образом: равенство (2) приводят к общему знаменателю, которым является  . Затем приравниваем числители в левой и правой части полученного равенства. Далее приравнивают коэффициенты при одинаковых степенях х в левой и правой части последнего равенства. В результате получим систему линейных уравнений относительно неопределенных коэффициентов. Решая эту систему, найдем неопределенные коэффициенты.
. Затем приравниваем числители в левой и правой части полученного равенства. Далее приравнивают коэффициенты при одинаковых степенях х в левой и правой части последнего равенства. В результате получим систему линейных уравнений относительно неопределенных коэффициентов. Решая эту систему, найдем неопределенные коэффициенты.
Таким образом, интегрирование всякой рациональной дроби сводится к интегрированию простейших рациональных дробей.
Лекция 3.
Тема: Интегрирование простейших рациональных дробей. Интегрирование тригонометрических выражений.
3.1. Интегрирование простейших рациональных дробей.




Выделим в числителе производную знаменателя



В подынтегральной функции в знаменателе выделим полный квадрат


Сначала в числителе выделим производную квадратного трехчлена
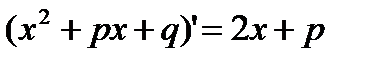

В последнем интеграле сделаем замену переменной 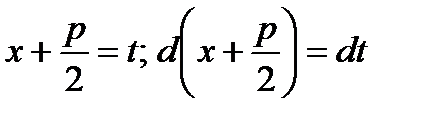

Нам остается вычислить интеграл

К последнему интегралу применим формулу интегрирования по частям

В результате получим

Итак, мы получили рекуррентную (возвратную) формулу
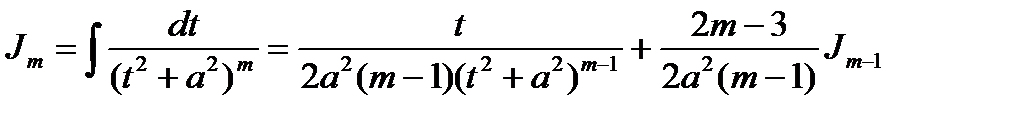
Применяя рекуррентную формулу вычисления интеграла  можно свести к вычислению интеграла
можно свести к вычислению интеграла 

Пример. Вычислить.  . В данном интеграле
. В данном интеграле 
 , где
, где  .
.
Для вычисления  снова применим рекуррентную формулу, где
снова применим рекуррентную формулу, где  .
.

Учитывая полученное, будем иметь:

Пример. Вычислить интеграл  . Во-первых, отметим, что подынтегральная функция является неправильной рациональной дробью, т.к. степень числителя больше степени знаменателя, поэтому поделим числитель на знаменатель и представим данную неправильную рациональную дробь в виде суммы многочлена и правильной рациональной дроби.
. Во-первых, отметим, что подынтегральная функция является неправильной рациональной дробью, т.к. степень числителя больше степени знаменателя, поэтому поделим числитель на знаменатель и представим данную неправильную рациональную дробь в виде суммы многочлена и правильной рациональной дроби.

Итак, имеем:


Теперь остается вычислить интеграл 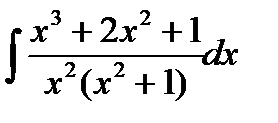 от правильной рациональной дроби. Для этого подынтегральную правильную рациональную дробь представили в виде суммы простейших рациональных дробей
от правильной рациональной дроби. Для этого подынтегральную правильную рациональную дробь представили в виде суммы простейших рациональных дробей




Учитывая полученный результат, будем иметь:

3.2. Интегрирование тригонометрических выражений.
Мы будем рассматривать
 , где
, где  есть рациональная функция от
есть рациональная функция от  и
и  . Т.е. если положить
. Т.е. если положить  , a
, a  , то
, то  есть отношение двух многочленов от
есть отношение двух многочленов от  .
.
Например:

Далее функция
 не является рациональной функцией от
не является рациональной функцией от  и
и  , т.к.
, т.к.  входит под знак корня.
входит под знак корня.
3.2.1. Универсальная подстановка.
Интеграл  с помощью подстановки
с помощью подстановки  всегда сводится к интегралу от рациональной функции:
всегда сводится к интегралу от рациональной функции:



В результате получаем:

Пример. Вычислить интеграл  , пользуясь указанной заменой переменной
, пользуясь указанной заменой переменной 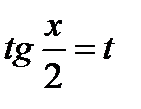 ,
,  ,
,  , получим:
, получим:

Пример. Вычислить интеграл 
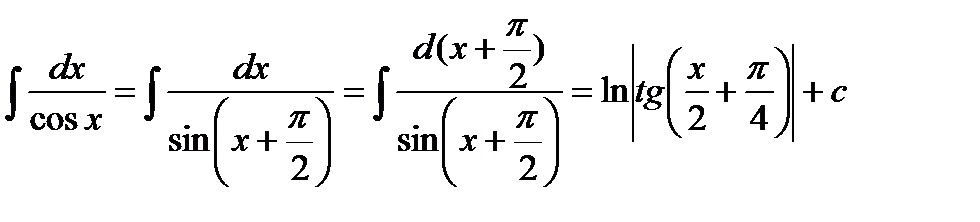
3.2.2. Теперь предположим, что  , т.е. подынтегральная функция нечетная относительно
, т.е. подынтегральная функция нечетная относительно  . В этом случае имеем:
. В этом случае имеем:
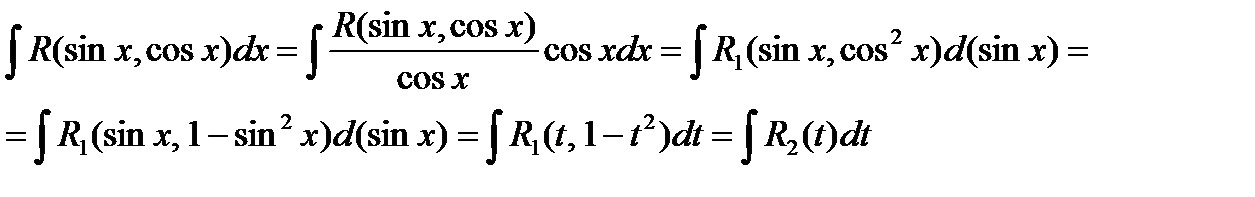
В этом случае была сделана замена  , и вычисление данного интеграла сводится к вычислению интеграла от рациональной функции.
, и вычисление данного интеграла сводится к вычислению интеграла от рациональной функции.
Пример. Вычислить интеграл:

3.2.3. Пусть  , т.е. подынтегральная функция нечетная относительно
, т.е. подынтегральная функция нечетная относительно  . В этом случае замена
. В этом случае замена  сводит вычисление
сводит вычисление  к вычислению интеграла от рациональной функции.
к вычислению интеграла от рациональной функции.
3.2.4. Теперь рассмотрим тот случай, когда
 , т.е. подынтегральная функция четная относительно
, т.е. подынтегральная функция четная относительно  и
и  одновременно. В этом случае замена
одновременно. В этом случае замена  позволяет свести вычисление интеграла
позволяет свести вычисление интеграла  к вычислению интеграла от рациональной функции. В самом деле,
к вычислению интеграла от рациональной функции. В самом деле,
 , т.к.
, т.к.
 , то функция
, то функция  является четной относительно
является четной относительно  , поэтому
, поэтому  и
и
 .
.

В результате замены переменной получим:

Пример. Вычислить интеграл  .
.
Подынтегральная функция является четной относительно  и
и  одновременно. Поэтому можно применить подстановку:
одновременно. Поэтому можно применить подстановку:  ,
,  . Имеем:
. Имеем:
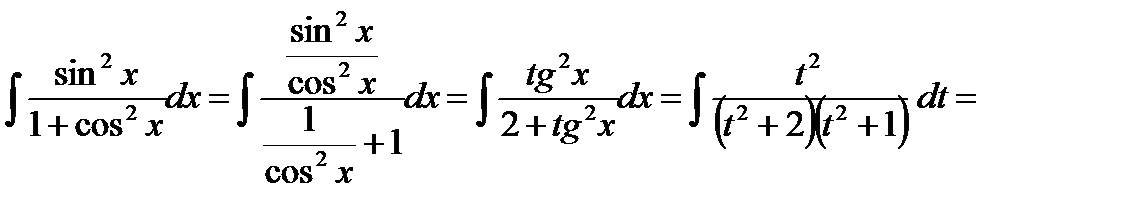
В последнем интеграле подынтегральная функция является правильной рациональной дробью, которую представим в виде суммы простейших рациональных дробей



Лекция 4.
Тема: Интегрирование некоторых иррациональных выражений. Примеры интегралов, не выражающихся в элементарных функциях.
4.1. Вычисление интегралов вида:  , где
, где  ,
,  символ рациональности функции.
символ рациональности функции.
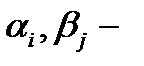 натуральные числа.
натуральные числа.
Пусть  наименьшее общее кратное.
наименьшее общее кратное.
В данном интеграле сделаем замену
 , тогда
, тогда  , где
, где  целое положительное число для любого
целое положительное число для любого 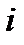 ,
,  .
.
Далее имеем:

 и
и 
Сделав подстановку, получим:

Таким образом, вычисление данного интеграла с помощью указанной замены сводится к вычислению интеграла от рациональной функции.
Пример. Вычислить интеграл  .
.
В данном интеграле сделаем замену: 
В результате замены получим:

Неправильную рациональную дробь  представим в виде суммы многочлена и правильной рациональной дроби, для этого поделим числитель на знаменатель:
представим в виде суммы многочлена и правильной рациональной дроби, для этого поделим числитель на знаменатель:

Таким образом, имеем:

4.2. Вычисление интегралов вида:

Выражение  означает следующее: если
означает следующее: если  , то
, то  есть рациональная функция от
есть рациональная функция от  .
.
Интегрирование данных выражений можно осуществить различными способами.
4.2.1. Интеграл  после выделения полного квадрата под знаком квадратного корня и замены
после выделения полного квадрата под знаком квадратного корня и замены  сводится к интегралу одного из следующего типов:
сводится к интегралу одного из следующего типов:
а) 
б) 
в) 
В свою очередь, последние три интеграла соответствующей подстановкой

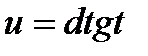

сводятся к интегралу вида:
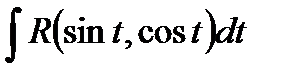
Пример. Вычислить: 
Выделяя полный квадрат в квадратном трехчлене x  +2x+3, получим:
+2x+3, получим:
 , где
, где  ,
, 
Делая подстановку 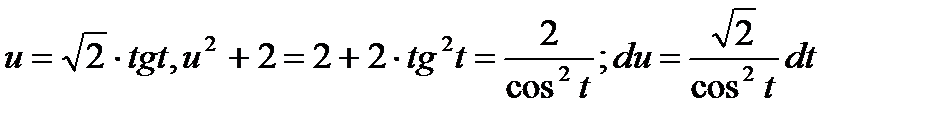 , получим:
, получим:

Пример. Вычислить: 
Делая подстановку  ,
,  ,
,  ,
,  получим:
получим:


4.2.2. Подстановка Эйлера.
Интеграл  ,
,  , может быть сведен к вычислению интеграла от рациональной функции с помощью подстановки
, может быть сведен к вычислению интеграла от рациональной функции с помощью подстановки  , которая носит имя Эйлера, впервые применившего эту подстановку.
, которая носит имя Эйлера, впервые применившего эту подстановку.
Пусть для определенности:

Возведем обе части последнего равенства в квадрат, в результате получим:

 ;
;  ;
;
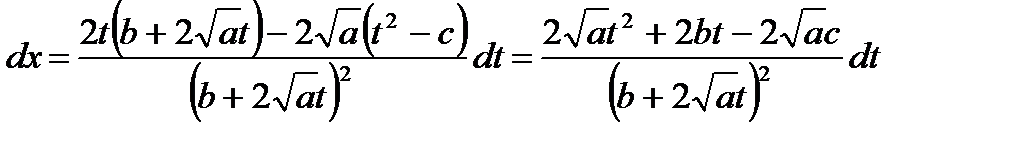

 .
.
Используя данную подстановку, будем иметь:
 ,
,
т.к. рациональная функция от рациональной функции есть рациональная функция и произведение двух рациональных функций есть рациональная функция.
Пример. Вычислить: 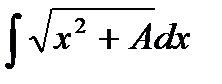
При вычислении данного интеграла используем подстановку Эйлера, т.к. коэффициент при x  больше 0.
больше 0.
 ;
;  ;
; 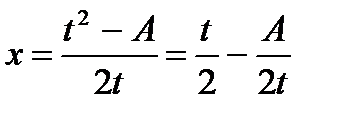 ;
;
 ;
;  ;
;
 .
.
Осуществляя подстановку, получим:

Пример. Вычислить: 
Применим снова подстановку Эйлера:
 ,
, 


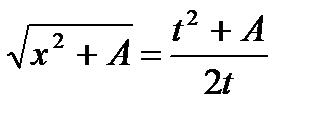 (см. пример 25)
(см. пример 25)
Далее имеем:

4.3. Примеры интегралов, не выражающихся в элементарных функциях:
 .
.
Лекция 5.
Тема: Задачи, приводящие к понятию определенного интеграла. Определение определенного интеграла, его свойства. Теорема существования определенного интеграла.
5.1 Задачи, приводящие к понятию определенного интеграла.
Задача 1. Вычислить площадь криволинейной трапеции.
Во-первых, мы должны дать определение криволинейной трапеции.
Во-вторых, должны дать определение площади криволинейной трапеции.
В-третьих, должны указать способ вычисления площади криволинейной трапеции.
Определение. Криволинейной трапецией называется фигура, ограниченная прямой l, двумя прямыми, перпендикулярными прямой l и непрерывной кривой, которая расположена по одну сторону от прямой l и любой прямой, перпендикулярной l, пересекается не более чем в одной точке.

Если прямую l взять за ось OX; OY  OX, тогда определение криволинейной трапеции можно дать следующим образом.
OX, тогда определение криволинейной трапеции можно дать следующим образом.
Определение. Криволинейной трапецией называется фигура, ограниченная осью OX, прямыми x=a; x=b и графиком непрерывной функции  ,
,  .
.

Далее, определение площади криволинейной трапеции и способ вычисления этой площади дадим одновременно.
При решении этих задач мы будем пользоваться следующими известными фактами:
1) Площадь фигуры есть неотрицательное число.
2) Если фигуру разбить на конечное число частей, то площадь всей фигуры равна сумме площадей ее частей.
3) Площадь прямоугольника равна произведению основания на высоту.
Криволинейную трапецию будем рассматривать в декартовой системе координат.
Отрезок  произвольным способом разобьем на n частей точками:
произвольным способом разобьем на n частей точками:
 . Это разбиение обозначим через (T),
. Это разбиение обозначим через (T),  . Через
. Через  обозначим наибольшую из длин
обозначим наибольшую из длин  ,
,  .
.
Далее, в каждом из отрезков разбиения произвольным способом выберем по точке  .
.
Прямые  , разобьют нашу криволинейную трапецию на n элементарных криволинейных трапеций. K- тую элементарную трапецию заменим прямоугольником с основанием
, разобьют нашу криволинейную трапецию на n элементарных криволинейных трапеций. K- тую элементарную трапецию заменим прямоугольником с основанием 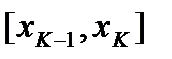 и высотой
и высотой  .
.
Тогда вся криволинейная трапеция заменится ступенчатой фигурой, состоящей из n прямоугольников, и площадь криволинейной трапеции будет приближенно равна площади ступенчатой фигуры.
Следовательно,  , где
, где  - площадь K- того прямоугольника.
- площадь K- того прямоугольника.
Символ  (греческая буква «сигма») обозначает сумму, т.е.
(греческая буква «сигма») обозначает сумму, т.е.
 .
.
Площадью криволинейной трапеции называют предел сумм  при
при  , т.е.
, т.е.  .
.
Тем самым мы одновременно дали определение площади криволинейной трапеции и указали способ ее вычисления.
Задача 2. Найти массу неоднородного стержня 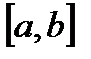 с плотностью
с плотностью  .
.
При решении этой задачи мы будем пользоваться следующими известными фактами:
1) Если плотность отрезка 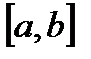 постоянна и равна
постоянна и равна  , то масса отрезка
, то масса отрезка  .
.
2) Если отрезок 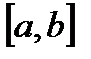 разбить на конечное число частей, то масса отрезка равна сумме масс его частей.
разбить на конечное число частей, то масса отрезка равна сумме масс его частей.
Теперь мы дадим определение массы неоднородного стержня 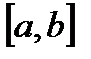 неоднородной плотности и укажем способ ее вычисления.
неоднородной плотности и укажем способ ее вычисления.
Отрезок 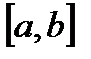 произвольным способом разобьем на n частей точками
произвольным способом разобьем на n частей точками  .
.
Это разбиение обозначим (T),  ,
, 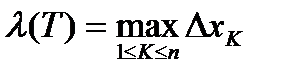 .
.
В каждом из отрезков разбиения произвольным способом выберем по точке  .
.
Масса К-того отрезка разбиения приближенно равна  , а масса всего стержня
, а масса всего стержня 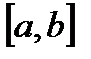 приближенно равна
приближенно равна  .
.
За массу стержня 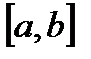 принимают предел сумм
принимают предел сумм  при
при  , т.е.
, т.е. 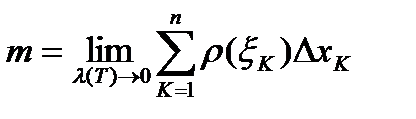 .
.
Таким образом, дано определение массы неоднородного стержня и указан способ ее вычисления.
Заметим, что многие другие задачи сводятся к вычислению пределов аналогичных сумм.
Отметим, если в задаче 1 и задаче 2 отвлечься от геометрического и механического смысла задач, то эти задачи решаются одним и тем же методом, т.е. решение задач сводится к нахождению пределов  .
.
5.2. Определение определенного интеграла.
Пусть  – произ
– произ



 в интервале
в интервале  называется функция
называется функция  , производная которой равна
, производная которой равна  , т.е.
, т.е.  .
. ,
,  , так как
, так как  . Легко заметить, что любая функция
. Легко заметить, что любая функция  является первообразной для функции
является первообразной для функции  , где
, где  – const.
– const. имеет одну первообразную
имеет одну первообразную  , то
, то  т.к.
т.к.  .
. в интервале имеет первообразную
в интервале имеет первообразную  , то любая другая первообразная отличается от данной на константу.
, то любая другая первообразная отличается от данной на константу. и
и  – две первообразные для функции
– две первообразные для функции  в интервале
в интервале  и
и  . Рассмотрим функцию
. Рассмотрим функцию  .
. дифференцируема в интервале
дифференцируема в интервале  принадлежащий
принадлежащий  , дифференцируема в интервале
, дифференцируема в интервале  . Следовательно,
. Следовательно,  , где
, где  некоторая точка интервала
некоторая точка интервала  .
. .Поэтому
.Поэтому  и
и  . Отсюда следует, что
. Отсюда следует, что  и
и  . ▼
. ▼ называют совокупность всех ее первообразных
называют совокупность всех ее первообразных  .
. .
. , где
, где  какая-либо одна из первообразных для
какая-либо одна из первообразных для  .
.  называется подынтегральной функцией,
называется подынтегральной функцией,  подынтегральным выражением.
подынтегральным выражением.
 одна из первообразных функции
одна из первообразных функции  , тогда
, тогда 
 .
.

 .
. 2)
2) 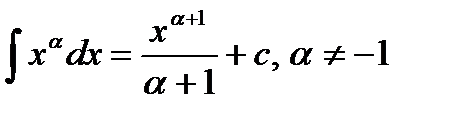 3)
3)  4)
4)  5)
5)  6)
6) 
 8)
8)  9)
9)  10)
10)  11)
11) 

 .
. и
и  .
. , где
, где  (1)
(1) первообразная для
первообразная для  тогда
тогда
 , где
, где 
 отсюда
отсюда  .
. , где
, где 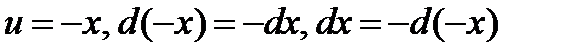


 , т.к.
, т.к. 
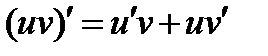

 отсюда получаем:
отсюда получаем:



 еще раз применим интегрирование по частям:
еще раз применим интегрирование по частям:
 , где
, где 
 , числитель которой есть производная знаменателя, то интеграл от этой дроби равен логарифму натуральному от модуля знаменателя!!!
, числитель которой есть производная знаменателя, то интеграл от этой дроби равен логарифму натуральному от модуля знаменателя!!!


 , где
, где  обратная функция для функции
обратная функция для функции  . Обратим внимание на то, что при замене переменной
. Обратим внимание на то, что при замене переменной 

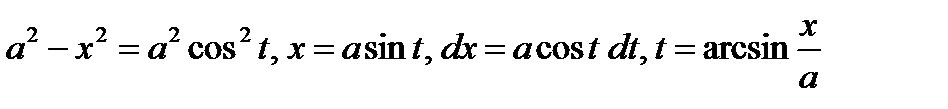

 , где
, где  и
и  многочлены соответственно степеней m и n.
многочлены соответственно степеней m и n. называется правильной, если степень числителя меньше степени знаменателя, т.е.
называется правильной, если степень числителя меньше степени знаменателя, т.е.  , в противном случае рациональная дробь – неправильная.
, в противном случае рациональная дробь – неправильная.

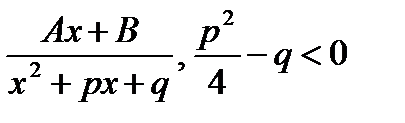

 .
. у многочлена
у многочлена  можно считать равным 1. Этого можно достичь, деля числитель и знаменатель на одно и то же число.
можно считать равным 1. Этого можно достичь, деля числитель и знаменатель на одно и то же число. имеет ровно n корней, учитывая их кратность, т.е.:
имеет ровно n корней, учитывая их кратность, т.е.: , где
, где  действительные корни,
действительные корни,  комплексные корни,
комплексные корни,  кратность соответствующих корней.
кратность соответствующих корней. комплексный корень
комплексный корень  , тогда
, тогда 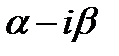 тоже корень
тоже корень 

 .
.









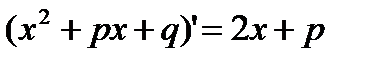

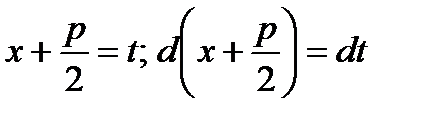




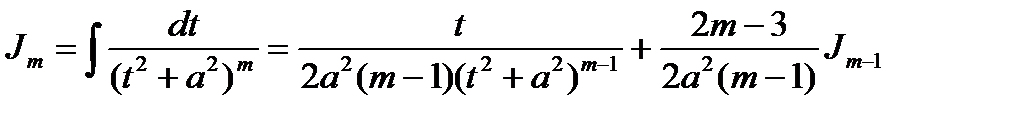
 можно свести к вычислению интеграла
можно свести к вычислению интеграла 

 . В данном интеграле
. В данном интеграле 
 , где
, где  .
. снова применим рекуррентную формулу, где
снова применим рекуррентную формулу, где  .
.

 . Во-первых, отметим, что подынтегральная функция является неправильной рациональной дробью, т.к. степень числителя больше степени знаменателя, поэтому поделим числитель на знаменатель и представим данную неправильную рациональную дробь в виде суммы многочлена и правильной рациональной дроби.
. Во-первых, отметим, что подынтегральная функция является неправильной рациональной дробью, т.к. степень числителя больше степени знаменателя, поэтому поделим числитель на знаменатель и представим данную неправильную рациональную дробь в виде суммы многочлена и правильной рациональной дроби.


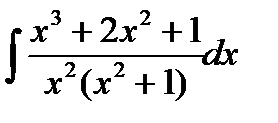 от правильной рациональной дроби. Для этого подынтегральную правильную рациональную дробь представили в виде суммы простейших рациональных дробей
от правильной рациональной дроби. Для этого подынтегральную правильную рациональную дробь представили в виде суммы простейших рациональных дробей




 , где
, где  есть рациональная функция от
есть рациональная функция от  и
и  . Т.е. если положить
. Т.е. если положить  , a
, a  , то
, то  есть отношение двух многочленов от
есть отношение двух многочленов от  .
.
 не является рациональной функцией от
не является рациональной функцией от  с помощью подстановки
с помощью подстановки  всегда сводится к интегралу от рациональной функции:
всегда сводится к интегралу от рациональной функции:



 , пользуясь указанной заменой переменной
, пользуясь указанной заменой переменной 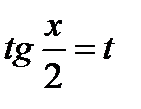 ,
,  ,
,  , получим:
, получим:

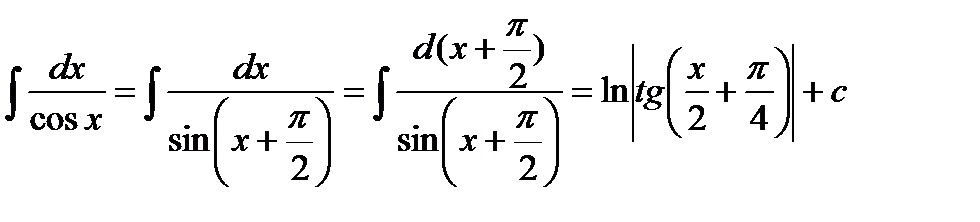
 , т.е. подынтегральная функция нечетная относительно
, т.е. подынтегральная функция нечетная относительно 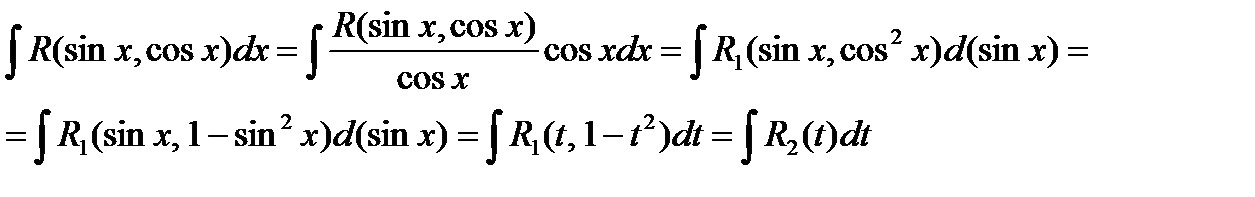
 , и вычисление данного интеграла сводится к вычислению интеграла от рациональной функции.
, и вычисление данного интеграла сводится к вычислению интеграла от рациональной функции.
 , т.е. подынтегральная функция нечетная относительно
, т.е. подынтегральная функция нечетная относительно  . В этом случае замена
. В этом случае замена  сводит вычисление
сводит вычисление  к вычислению интеграла от рациональной функции.
к вычислению интеграла от рациональной функции. , т.е. подынтегральная функция четная относительно
, т.е. подынтегральная функция четная относительно  и
и  одновременно. В этом случае замена
одновременно. В этом случае замена 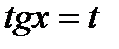 позволяет свести вычисление интеграла
позволяет свести вычисление интеграла  к вычислению интеграла от рациональной функции. В самом деле,
к вычислению интеграла от рациональной функции. В самом деле, , т.к.
, т.к. , то функция
, то функция  является четной относительно
является четной относительно  , поэтому
, поэтому  и
и .
.

 .
. ,
,  . Имеем:
. Имеем: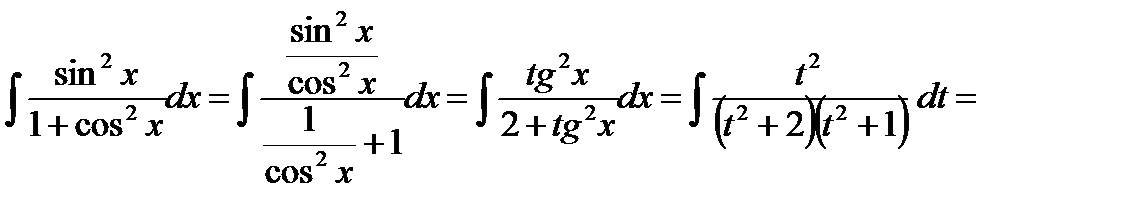



 , где
, где  ,
,  символ рациональности функции.
символ рациональности функции. натуральные числа.
натуральные числа. наименьшее общее кратное.
наименьшее общее кратное. , тогда
, тогда  , где
, где  целое положительное число для любого
целое положительное число для любого  ,
,  .
.
 и
и 

 .
.

 представим в виде суммы многочлена и правильной рациональной дроби, для этого поделим числитель на знаменатель:
представим в виде суммы многочлена и правильной рациональной дроби, для этого поделим числитель на знаменатель:


 означает следующее: если
означает следующее: если  , то
, то  есть рациональная функция от
есть рациональная функция от  .
. после выделения полного квадрата под знаком квадратного корня и замены
после выделения полного квадрата под знаком квадратного корня и замены  сводится к интегралу одного из следующего типов:
сводится к интегралу одного из следующего типов:



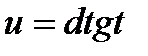

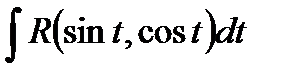

 +2x+3, получим:
+2x+3, получим: , где
, где  ,
, 
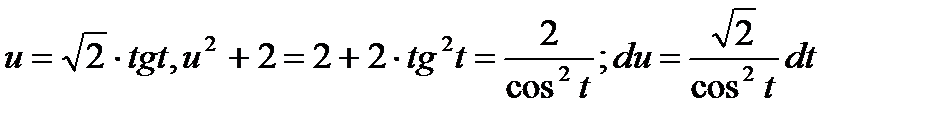 , получим:
, получим:

 ,
,  ,
,  ,
,  получим:
получим:

 ,
,  , может быть сведен к вычислению интеграла от рациональной функции с помощью подстановки
, может быть сведен к вычислению интеграла от рациональной функции с помощью подстановки  , которая носит имя Эйлера, впервые применившего эту подстановку.
, которая носит имя Эйлера, впервые применившего эту подстановку.

 ;
;  ;
;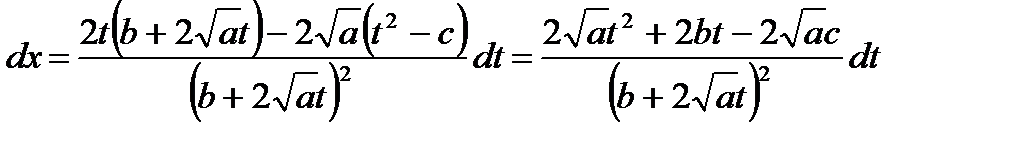

 .
. ,
,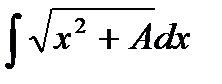
 ;
;  ;
; 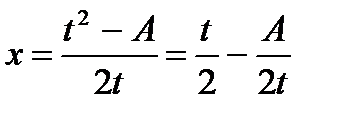 ;
; ;
;  ;
; .
.




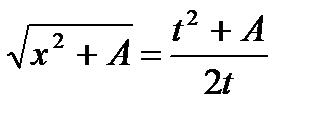 (см. пример 25)
(см. пример 25)
 .
.
 OX, тогда определение криволинейной трапеции можно дать следующим образом.
OX, тогда определение криволинейной трапеции можно дать следующим образом. ,
,  .
.
 произвольным способом разобьем на n частей точками:
произвольным способом разобьем на n частей точками: . Это разбиение обозначим через (T),
. Это разбиение обозначим через (T),  . Через
. Через  обозначим наибольшую из длин
обозначим наибольшую из длин  ,
,  .
. .
. , разобьют нашу криволинейную трапецию на n элементарных криволинейных трапеций. K- тую элементарную трапецию заменим прямоугольником с основанием
, разобьют нашу криволинейную трапецию на n элементарных криволинейных трапеций. K- тую элементарную трапецию заменим прямоугольником с основанием 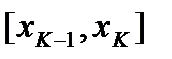 и высотой
и высотой  .
. , где
, где  - площадь K- того прямоугольника.
- площадь K- того прямоугольника. (греческая буква «сигма») обозначает сумму, т.е.
(греческая буква «сигма») обозначает сумму, т.е. .
. при
при  , т.е.
, т.е.  .
. .
. , то масса отрезка
, то масса отрезка  .
. .
. ,
, 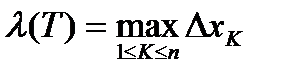 .
. .
. , а масса всего стержня
, а масса всего стержня  .
. при
при  , т.е.
, т.е. 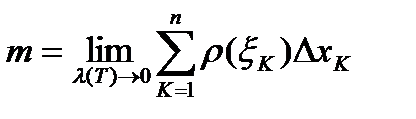 .
. .
. – произ
– произ