 , где
, где  -постоянные числа, называемые коэффициентами ряда,
-постоянные числа, называемые коэффициентами ряда,  -фиксированное число.При
-фиксированное число.При 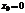 получаем степенной ряд вида
получаем степенной ряд вида
 . Ряд (1) легко приводится к ряду (2), если положить
. Ряд (1) легко приводится к ряду (2), если положить  . Поэтому при изучении степенных рядов иногда ограничиваются степенным рядом (2).
. Поэтому при изучении степенных рядов иногда ограничиваются степенным рядом (2).
Выясним вопрос о сходимости степенного ряда (7.3). Область сходимости этого степенного ряда содержит, по крайней мере, одну точку  (ряд (1) сходится в точке
(ряд (1) сходится в точке  ).
).
Об области сходимости степенного ряда можно судить, исходя из следующей теоремы. Теорема (теорема Абеля). Если степенной ряд (7.3) сходится в точке  , то он абсолютно сходится при всех
, то он абсолютно сходится при всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству  .Из теоремы Абеля следует, что если
.Из теоремы Абеля следует, что если 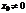 есть точка сходимости степенного ряда, то интервал
есть точка сходимости степенного ряда, то интервал  весь состоит их точек сходимости данного ряда; при всех значениях
весь состоит их точек сходимости данного ряда; при всех значениях  вне этого интервала ряд (7.3) расходится.Пусть
вне этого интервала ряд (7.3) расходится.Пусть  . Интервал
. Интервал 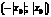 или
или  называют интервалом сходимости. Число
называют интервалом сходимости. Число  называют радиусом сходимости степенного ряда. Таким образом,
называют радиусом сходимости степенного ряда. Таким образом,  - это такое число, что при всех
- это такое число, что при всех  , для которых
, для которых  , ряд (7.3) абсолютно сходится, а при
, ряд (7.3) абсолютно сходится, а при  ряд расходится.Отметим, что на концах интервала сходимости (т.е. при
ряд расходится.Отметим, что на концах интервала сходимости (т.е. при  и при
и при  ) сходимость ряда проверяется в каждом случае отдельно.В частности, когда ряд (7.3) сходится лишь в одной точке
) сходимость ряда проверяется в каждом случае отдельно.В частности, когда ряд (7.3) сходится лишь в одной точке  , то считаем, что
, то считаем, что 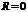 . Если же ряд (7.3) сходится при всех значениях
. Если же ряд (7.3) сходится при всех значениях  (т.е. во всех точках числовой оси), то считаем, что
(т.е. во всех точках числовой оси), то считаем, что  .
.
Для нахождения радиуса сходимости степенного ряда (7.3) можно поступить следующим образом. Составим ряд из модулей членов данного степенного ряда

и применим к нему признак Даламбера. Допустим, что существует предел
 .
.
По признаку Даламбера ряд сходится, если  , т.е. ряд сходится при тех значениях
, т.е. ряд сходится при тех значениях  , для которых
, для которых
 .
.
Ряд, составленный из модулей членов ряда (7.3), расходится при тех значениях  , для которых
, для которых  .
.
Таким образом, для ряда (7.3) радиус сходимости
 . (7.4)
. (7.4)
Аналогично, воспользовавшись радикальным признаком Коши, можно получить, что
 . (7.5)
. (7.5)
Замечания:Если  , то ряд (7.3) абсолютно сходится на всей числовой оси. В этом случае
, то ряд (7.3) абсолютно сходится на всей числовой оси. В этом случае  . Если
. Если  , то
, то 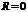 .
.
Если дан степенной ряд (7.2), то его радиус сходимости определяется также по формулам (7.4) или (7.5), а интервал сходимости будет интервал с центром в точке  :
: 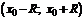 .
.
Свойства степенных рядов.
Сформулируем без доказательства основные свойства степенных рядов.
1)Сумма  степенного ряда (7.3) является непрерывной функцией в интервале сходимости
степенного ряда (7.3) является непрерывной функцией в интервале сходимости  .
.
2)Степенные ряды  и
и  , имеющие радиусы сходимости соответственно
, имеющие радиусы сходимости соответственно  и
и  , можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядов не меньше, чем меньшее из числе
, можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядов не меньше, чем меньшее из числе  и
и  .
.
3)Степенной ряд внутри интервала сходимости можно почленно дифференцировать. Для ряда

при 
 . (7.6)
. (7.6)
4)Степенной ряд можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости. Для ряда (7.3) при  выполняется равенство
выполняется равенство
 Ряды (7.6) и (7.7) имеют тот же радиус сходимости, что и исходный степенной ряд. Перечисленные свойства остаются справедливыми и для степенных рядов вида.
Ряды (7.6) и (7.7) имеют тот же радиус сходимости, что и исходный степенной ряд. Перечисленные свойства остаются справедливыми и для степенных рядов вида.
Ряды Тейлора и Маклорена.
Для приложений важно уметь данную функцию  представлять в виде суммы степенного ряда.Для любой функции
представлять в виде суммы степенного ряда.Для любой функции  , определенной в окрестности точки
, определенной в окрестности точки  и имеющей в ней производные до
и имеющей в ней производные до  -го порядка включительно, справедлива формула Тейлора:
-го порядка включительно, справедлива формула Тейлора:
 ,
,
где  , - остаточный член в форме Лагранжа. Причем число
, - остаточный член в форме Лагранжа. Причем число  можно записать в виде
можно записать в виде  , где
, где 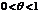 .
.
Формулу (7.8) можно записать в виде
 ,
,
где  - многочлен Тейлора.
- многочлен Тейлора.
Если функция  имеет производные любых порядков (т.е. бесконечно дифференцируема) в окрестности точки
имеет производные любых порядков (т.е. бесконечно дифференцируема) в окрестности точки  и остаточный член
и остаточный член  стремится к нулю при
стремится к нулю при  (
( ), то из формулы Тейлора получается разложение функции
), то из формулы Тейлора получается разложение функции 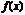 по степени
по степени  , называемое рядом Тейлора:
, называемое рядом Тейлора:
 Если в ряде Тейлора положить
Если в ряде Тейлора положить  , то получим разложение функции по степеням
, то получим разложение функции по степеням  в так называемый ряд Маклорена:
в так называемый ряд Маклорена:

Отметим, что ряд Тейлора можно формально построить для любой бесконечно дифференцируемой функции (это необходимое условие) в окрестности точки  . Но отсюда еще не следует, что он будет сходиться к данной функции
. Но отсюда еще не следует, что он будет сходиться к данной функции 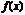 ;он может оказаться расходящимся или сходится, но не к функции
;он может оказаться расходящимся или сходится, но не к функции  .
.
В следующей теореме (которую примем без доказательства) сформулировано необходимое и достаточное условие сходимости ряда Тейлора к функции 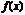 .
.
Теорема Для того чтобы ряд Тейлора (7.9) функции  сходился к функции
сходился к функции 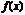 в точке
в точке  , необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора (7.8) стремился к нулю при
, необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора (7.8) стремился к нулю при  , т.е. чтобы
, т.е. чтобы  .
.
Для разложения функции  в ряд Маклорена (7.10) нужно:
в ряд Маклорена (7.10) нужно:
1. найти производные  ;
;
2. вычислить значения производных в точке 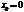 ;
;
3. выписать ряд (7.10) для заданной функции и найти его интервал сходимости;
4. найти интервал  , в котором остаточный член ряда Маклорена
, в котором остаточный член ряда Маклорена 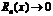 при
при  . Если такой интервал существует, то в нем функция
. Если такой интервал существует, то в нем функция  и сумма ряда Маклорена совпадают.
и сумма ряда Маклорена совпадают.



 , где
, где  -постоянные числа, называемые коэффициентами ряда,
-постоянные числа, называемые коэффициентами ряда,  -фиксированное число.При
-фиксированное число.При 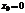 получаем степенной ряд вида
получаем степенной ряд вида . Ряд (1) легко приводится к ряду (2), если положить
. Ряд (1) легко приводится к ряду (2), если положить  . Поэтому при изучении степенных рядов иногда ограничиваются степенным рядом (2).
. Поэтому при изучении степенных рядов иногда ограничиваются степенным рядом (2). (ряд (1) сходится в точке
(ряд (1) сходится в точке  ).
). , то он абсолютно сходится при всех
, то он абсолютно сходится при всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству  .Из теоремы Абеля следует, что если
.Из теоремы Абеля следует, что если 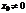 есть точка сходимости степенного ряда, то интервал
есть точка сходимости степенного ряда, то интервал  весь состоит их точек сходимости данного ряда; при всех значениях
весь состоит их точек сходимости данного ряда; при всех значениях  вне этого интервала ряд (7.3) расходится.Пусть
вне этого интервала ряд (7.3) расходится.Пусть  . Интервал
. Интервал 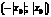 или
или  называют интервалом сходимости. Число
называют интервалом сходимости. Число  называют радиусом сходимости степенного ряда. Таким образом,
называют радиусом сходимости степенного ряда. Таким образом,  - это такое число, что при всех
- это такое число, что при всех  , для которых
, для которых  , ряд (7.3) абсолютно сходится, а при
, ряд (7.3) абсолютно сходится, а при  ряд расходится.Отметим, что на концах интервала сходимости (т.е. при
ряд расходится.Отметим, что на концах интервала сходимости (т.е. при  и при
и при  ) сходимость ряда проверяется в каждом случае отдельно.В частности, когда ряд (7.3) сходится лишь в одной точке
) сходимость ряда проверяется в каждом случае отдельно.В частности, когда ряд (7.3) сходится лишь в одной точке  , то считаем, что
, то считаем, что 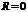 . Если же ряд (7.3) сходится при всех значениях
. Если же ряд (7.3) сходится при всех значениях  (т.е. во всех точках числовой оси), то считаем, что
(т.е. во всех точках числовой оси), то считаем, что  .
.
 .
. , т.е. ряд сходится при тех значениях
, т.е. ряд сходится при тех значениях  , для которых
, для которых .
. .
. . (7.4)
. (7.4) . (7.5)
. (7.5) , то ряд (7.3) абсолютно сходится на всей числовой оси. В этом случае
, то ряд (7.3) абсолютно сходится на всей числовой оси. В этом случае  , то
, то  :
: 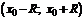 .
. степенного ряда (7.3) является непрерывной функцией в интервале сходимости
степенного ряда (7.3) является непрерывной функцией в интервале сходимости  .
. и
и  , имеющие радиусы сходимости соответственно
, имеющие радиусы сходимости соответственно  и
и  , можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядов не меньше, чем меньшее из числе
, можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядов не меньше, чем меньшее из числе  и
и  .
.

 . (7.6)
. (7.6) Ряды (7.6) и (7.7) имеют тот же радиус сходимости, что и исходный степенной ряд. Перечисленные свойства остаются справедливыми и для степенных рядов вида.
Ряды (7.6) и (7.7) имеют тот же радиус сходимости, что и исходный степенной ряд. Перечисленные свойства остаются справедливыми и для степенных рядов вида. представлять в виде суммы степенного ряда.Для любой функции
представлять в виде суммы степенного ряда.Для любой функции  , определенной в окрестности точки
, определенной в окрестности точки  и имеющей в ней производные до
и имеющей в ней производные до  -го порядка включительно, справедлива формула Тейлора:
-го порядка включительно, справедлива формула Тейлора: ,
, , - остаточный член в форме Лагранжа. Причем число
, - остаточный член в форме Лагранжа. Причем число  можно записать в виде
можно записать в виде  , где
, где 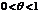 .
. ,
, - многочлен Тейлора.
- многочлен Тейлора. имеет производные любых порядков (т.е. бесконечно дифференцируема) в окрестности точки
имеет производные любых порядков (т.е. бесконечно дифференцируема) в окрестности точки  и остаточный член
и остаточный член  стремится к нулю при
стремится к нулю при  (
( ), то из формулы Тейлора получается разложение функции
), то из формулы Тейлора получается разложение функции 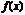 по степени
по степени  , называемое рядом Тейлора:
, называемое рядом Тейлора: Если в ряде Тейлора положить
Если в ряде Тейлора положить  , то получим разложение функции по степеням
, то получим разложение функции по степеням 
 . Но отсюда еще не следует, что он будет сходиться к данной функции
. Но отсюда еще не следует, что он будет сходиться к данной функции  .
. сходился к функции
сходился к функции  , т.е. чтобы
, т.е. чтобы  .
. ;
;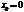 ;
; , в котором остаточный член ряда Маклорена
, в котором остаточный член ряда Маклорена 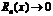 при
при  и сумма ряда Маклорена совпадают.
и сумма ряда Маклорена совпадают.

