Из фотографий лекций – рис 27
Теоремы о численности множеств. Задачи.
 Теорема: (для 2-х множеств) | AUB|+ |AUB|=|A|+|B|. Док-во: Если сложитьA| и |B|, то сумма будет больше | AUB| на | AUB|, т.к. эл-ты пересечения были сосчитаны дважды.
Теорема: (для 2-х множеств) | AUB|+ |AUB|=|A|+|B|. Док-во: Если сложитьA| и |B|, то сумма будет больше | AUB| на | AUB|, т.к. эл-ты пересечения были сосчитаны дважды.
Теорема для 3-х множеств: |AUBUC|=|A|+|B|+|C|- |A  B|-|B
B|-|B  C|-|C
C|-|C  A|+|A
A|+|A  B
B  C|
C|
 Доказательство:Если сложить ||A|, |B|, |C|, то сумма будет больше модуля |AUBUC| на |A
Доказательство:Если сложить ||A|, |B|, |C|, то сумма будет больше модуля |AUBUC| на |A  B|+|B
B|+|B  C|+|C
C|+|C  A| поэтому эту сумму надо вычесть. Однако при этом элементы из А
A| поэтому эту сумму надо вычесть. Однако при этом элементы из А  B
B  C не будут учтены ни разу(сначала их трижды сосчитали, а потом вычли), поэтому надо прибавить ||A
C не будут учтены ни разу(сначала их трижды сосчитали, а потом вычли), поэтому надо прибавить ||A  B
B  C|, тогда получим |AUBUC|.
C|, тогда получим |AUBUC|.
Задача: В группе 30 человек, кот-е изучают английский, немецкий, французский и китайский языки. 15 чел. изучают англ. яз., 14 –нем., 13-французский. Англ. и нем. изучают 9, нем. и фр.-8, фр. и англ. -7 чел., 3-е изучают 3 эти языка (англ., нем., фр.) Есть ли студенты, изучающие только немецкий? Только китайский язык? Сколько их? А также изучающих по одному или по 2 европейских языка? По одному языку? Решение: 30.
Замечание: можно понимать, что 9 человек изучают англ. и нем. без фр., а можно с францезским.
 В 1-ом случае (рис. выше): 9,8,7,3. Во 2-м случае- что же делать?(будем писать в центре 3, а дальше 6, 5, 4). Мы заметим, что 1-ый случай не может иметь места.(условие можно понимать только как 2-ой случай). Т.о. Т.к. |E
В 1-ом случае (рис. выше): 9,8,7,3. Во 2-м случае- что же делать?(будем писать в центре 3, а дальше 6, 5, 4). Мы заметим, что 1-ый случай не может иметь места.(условие можно понимать только как 2-ой случай). Т.о. Т.к. |E  D|=9,то |E
D|=9,то |E  D
D  не F|=9-3=6(чел. изучают англ. и нем. и не изучают французский).
не F|=9-3=6(чел. изучают англ. и нем. и не изучают французский).
Аналогично |D  F
F  не Е|=8-3=5(изуч. нем. и фр. но не изуч. англ. яз.), |F
не Е|=8-3=5(изуч. нем. и фр. но не изуч. англ. яз.), |F  E
E  не D|=7-3=4(не изуч. нем.)
не D|=7-3=4(не изуч. нем.)
После этого ищем тех, кто изучает только английский: |E  неD
неD  не F|=15-(6+4+3) = 2, только немецкий язык:
не F|=15-(6+4+3) = 2, только немецкий язык:
|D  не F
не F  не Е|=14-6-5-3=0-таких студентов нет. Изучающие только французский: | F
не Е|=14-6-5-3=0-таких студентов нет. Изучающие только французский: | F  не D
не D  не Е|=13-4-5-3=1.
не Е|=13-4-5-3=1.
После этого находим: |не E  неD
неD  не F|=30-15-1-0-5=9- они изучают китайский язык. Только нем. не изучает никто.
не F|=30-15-1-0-5=9- они изучают китайский язык. Только нем. не изучает никто.
Тождественные преобразования в алгебре множеств.
Основные понятия. Примеры.
Говорят, что между мно-вами А и В задано соответствие f, если хотя бы одному элементу из А соответствует что-то из В.
a f b (b=f(a), a→b). элементу а из А по закону f соответствует b из В.
Множество всех преобразований называется областью определения соответствия f и обозначается D(f).
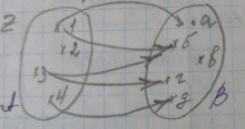 Граф соответствия f – это
Граф соответствия f – это
Мы видим, что 1 f a, 1 →б, б=f(3), 3fг, 4fд, а также, что D(f) = {1,3,4}, E(f) = {а, б, г, д}.
Понятно, что (область определения часть) D(f) c A, E(f) c B.
График соответствия f – это множество G(f) всех пар вида (a.b), где a f b. Понятно, что G(f) c AxB
У нас G(f) = {(1,a), (2, б), (3, г), (4, д)}
Частные виды соответствий: всюду определённые, сюръекции, функции, инъекции (а также отображения и биекции). Особенности графов и матриц.
Обратные соответствие f -1 и его свойства.
О композиции f о g соответствий f и g. Ассоциативность композиций.
Примеры биекций. свойства биекций.
Определения. 1) Если f одновременно всюду определено и функция, то f – отображением A в B. (На графе: из каждой точки A только одна стрелка. f – всюду определенное (D(f)=A. На графе: из каждой точки A должна выходить хотя бы одна стрелка.)).
2) Соответствие f – биекция (f одновременно сюръекция, функция и инъекция (равночисленность множеств). f – сюръекция (E(f)=B. На графе: к каждой точке B должна подходить хотя бы одна стрелка). f – функция (у каждого элемента из A не более одного образа в B (1 или 0). На графе: из каждой точки A выходит не более 1 стрелки). f – инъекция (у каждого элемента из B не более 1 прообраза в A. На графе: к каждой точке B подходит не более 1 стрелки).).
Примеры биекции: 1) Если f – биекция между конечными множествами A и B, то можно понять, что эти множества должны быть равночисленными (|A|=|B|).
2) N: 1, 2, 3, 4, 5, …; N0: 0, 1, 2, 3, 4, …; f(n)=n-1 (биекция) не трудно убедиться, что f – биекция, проверяем является ли оно сюръекцией, функцией и инъекцией).
3) N: 1, 2, 3, 4, 5, …; N2: 2, 4, 6, 8, 10, …; f(n)=2n (биекция)
4) N и веревка с узлами. Биекция между N и узлами этой веревки устанавливается легко.
Равномощность множеств. Примеры. Счётные множества и множества мощности континуум.
Рассмотрим два множества A и B.
Отображение ƒ из A в B (обозначается ƒ: A→B) — это правило, которое каждому элементу множества A ставит в соответствие элемент множества B, причём ровно один. (При этом не запрещается двум элементам множества A ставить в соответствие один и тот же элемент множества B, рис. 1, а.)
Отображение ƒ называется взаимно однозначным, если каждый элемент множества B поставлен в соответствие ровно одному элементу множества A (рис. 1, б).
Множества A и B называются равномощными, если существует взаимно однозначное отображение ƒ:A→B. Понимать это можно так: множества равномощны, если в них одинаковое количество элементов.
Например, множества {0, 1, 2} и {лошадь, корова, телевизор} равномощны, а множества {0, 1, 2} и {лошадь, корова} неравномощны (телевизор был по делу...).
Определение Множества, эквивалентные по числу элементов множеству N={1, 2, 3, 4, …} называются счетными множествами.
Примеры счетных множеств:
{2, 4, 6, 8, …};;{1, 4, 9, 16, 25, …}; {1, 8, 27, 64, 125, …}
Свойства счетных множеств изложим, пользуясь терминологией математики, т.е. громко именуя их теоремами.
Теорема 1. Для того, чтобы множество А было счетным, необходимо и достаточно, чтобы его можно было представить в виде А={a1, a2, a3,…}
Бинарные отношения на множестве. Примеры. Частные виды. Особенности графов и матриц.*)
Определение. Про соответствие f между множествами A и B в случае, когда эти множества равны (A=B), можно говорить, что это бинарное отношение на множестве A. Таким образом бинарное отношение это частный случай соответствия. Поэтому для бинарных отношений справедливо все, что верно для соответствий.
Примеры. 1) A=N Пусть afb, если a  b. Например, 1f1, но 1
b. Например, 1f1, но 1  2, 13f1, но 13
2, 13f1, но 13  7.
7.
2) A – тоже, но afb, если натуральное a кратно простому b. Это другой пример, так как здесь на втором месте не может быть 1, т.к. оно не простое (простое – N, у которого ровно 2 делителя; составное – N, у которого больше двух делителей).
3) A={1, 2, 3, …, 9} Пусть afb, если a≤b. Например, 0≤ любого b, любое a≤9, но 3  2.
2.
Определения. 1. f называется рефлексивным отношением, если всегда afa, т.е. любой элемент a находится в отношение f сам с собой. На графе такого отношения каждая точка снабжена петлей.
Примеры. 1) Быть кратным на N (но не на N0). 2) Быть родственниками. 3) Быть не выше (но не «быть выше»).
2. В последнем случае, когда всегда a не f a, говорят что f антирефлексивно. В этом случае на графе нет ни одной петли.
3. f называется симметричным отношением, если из afb всегда следует bfa. На графе все стрелки вот такие:↔.
4. Если же для различных a и b из afb всегда следует b не f a, то такое f называют антисимметричным.
Примеры. 1) быть знакомыми, 2) быть одного возраста, 3) учиться в одном классе, 4) иметь одних и тех же родителей и т.д., 5) быть мамой своего ребенка, 6) быть длиннее на множестве отрезков.
5. f называется транзитивным отношением, если из afb,bfc всегда следует afc. На графе все цепочки должны быть замкнуты.
6. Если же f одновременно рефлексивно, симметрично и транзитивно, то оно называется отношением эквивалентности.
Примеры. 1) Учиться в одном классе. 2) Родиться в одном и том же году или в одном и том же месте. 3) Начинаться с одинаковой буквы, но не иметь «хотя бы одну» одинаковую букву (мама f мыла, мыла f рыльце, но мама не f рыльце).
Отношение эквивалентности. Примеры. Класса эквивалентности.
Отношение R на мн-ве Х наз отношением эквивалент
ности, если оно одновременно обладает cв-вами рефлексивности, симметричности и транзитивности.
Если на.мн-ве Х задано отношение эквuва лентности, то оно порождает разбиение этого мн-ва на попарно непересекающиеся подмн-ва (классы эквивалентности).
Бинарным отношением на мн-ве Х наз всякое подмн-во декартова произведения ХCХ.
1º R рефлексивно на Х Û хRх для любого хÎХ. P
2º симметрично хRу Û уRу (туда-сюда)
3º транзитивности хRу, уRz } хRz хªу, уªz I хªz
Классы: 1. элементы одного класса эквивалентности взаимозаменяемы. Так в дробь 3/6 можно заменить на ½.
2. класс эквивалентности опр-ся любым своим представителем
3. разбиение мн-ва на классы исп-ся для введения новых понятий.
Отношение R на мн-вe Х наз отношением порядка, если оно одновременно обладает св-вом антисuмметричности и транзитивности. Примеры: отношения «меньше» на мн-ве N, «короче» на мн-ве отрезков.
Теорема. 1. Каждое отношение эквивалентности порождает разбиение мн-ва на классы, подчиненное данному отношению.
Теорема. 2. Если есть разбиение на мн-ва М на классы, то существует отношение эквивалентности на этом мн-ве М, которому подчинено данное разбиение.
Отношения порядка. Примеры.
Определение. Бинарное отношение f на M называется отношением порядка, если f транзитивно и антисимметрично (т.е. для различных a и b из afb всегда следует bfa). Можно сказать что из afb и bfa всегда следует, что a=b.
Примеры. 1) N0={0, 1, 2, 3, …}. Отношения >, <, ≤, ≥ транзитивны и антисимметричны (a>b следовательно b>a). 2) A – все студенты. Пусть afb, если a – не старше b (выше, тяжелее, веселее и т.д.). Если под «не старше» понимать что человек a родился в тот же день, что и b, или позже, то антисимметричности нет, т.к. есть «нарушители» - «однодневки». Если учитывать еще и время рождения, то это отношение антисимметрично. 3) T – множество треугольников. afb, если Sa>Sb. f – транзитивно и антисимметрично. 4)  . Попробуем ввести в этом множестве отношение порядка.
. Попробуем ввести в этом множестве отношение порядка.  , если a<b – порядок.
, если a<b – порядок.  , если a и b взаимно простые числа. g – не транзитивно. Контрпример:
, если a и b взаимно простые числа. g – не транзитивно. Контрпример:  ,
,  , но
, но  .
.
Частные виды порядков: Определения. Порядок f называется строгим, если он антирефлексивен, т.е. всегда afa. Порядок f называется нестрогим, если он рефлексивен.
Примеры. В рассмотренных выше примерах строгими будут из 1) отношения <, >; отношения порядка из 3) и из 4). К нестрогим порядкам относятся из 1) примера отношения ≤, ≥; из 2) примера отношения порядка.
Определение. Порядок f называется линейным, если для любых различных a и b справедливо afb или bfa.
Примеры. Порядок из примера 1) будет строгим (<, >) или нестрогим (≤, ≥) линейным порядком; порядок из 2) примера.
БАО как отображение МxМ М. Свойства и примеры БАО.
Определение. Если на некотором множестве M задан закон, по которому любым двум элементам a и b из M (может быть a=b) сопоставляется вполне определенный элемент a*b из этого же множества то говорят, что на M задана бинарная алгебраическая операция *.
Примеры. 1) сложение и вычитание на множестве всех векторов, 2) конъюнкция, дизъюнкция, импликация, разделительная дизъюнкция, штрих Шеффера и стрелка Пирса на множестве всех высказываний, 3) сложение, умножение, вычитание и деление на множестве целых чисел, 4) объединение, пересечение, разность множеств, декартово произведение множеств.
Свойства:
1) Коммутативность. БАО коммутативно, если для любых а и b из M выполняется равенство а*b=b*а. Примеры. 2∙5=5∙2.
2) Ассоциативность. БАО ассоциативно, если для любых а, b и c из M выполняется равенство (а*b)*c=а*(b*c). Примеры. (4+7)+9=4+(7+9).
3) Идемпотентность. БАО идемпотентно, если для любого а из M выполняется равенство а*а=а. Примеры. 1∙(:)1=1, 0+0=0.
4) Нейтральный и поглощающий элементы (левый, правый, просто). Нейтральный элемент e из множества M относительно БАО, если для любого элемента a из M выполняется равенство e*a=a или a*e=a. Примеры. 2+0=0+2=2 (для сложения в Z – 0), 2∙1=1∙2=2 (для умножения в Z – 1), 2-0=2 (правый нейтральный элемент для вычитания).
Поглощающий элемент e из множества M относительно БАО, если для любого элемента a из M выполняется равенство e*a=е или a*e=е. 2∙0=0∙2=0 (для сложения в Z – 0), 0:2=0 (левый поглощающий элемент для вычитания).
5) Дистрибутивность (левый, правый, просто). БАО ◦ дистрибутивно относительно БАО *, если для любых элементов а, b и c из M выполняются равенства (a*b)◦c=(a◦c)*(b◦c), c◦(a*b)=(c◦a)*(c◦b). Примеры. (1+3)∙6=(1∙6)+(3∙6), 6∙(1+3)=(6∙1)+(6∙3).
6) Закон поглощения. Если для любых а и b из M выполняется равенство (a*b)◦a=a◦(a*b)=a, то это закон поглащения. Примеры. (АvВ)ʌA=Aʌ(АvВ)=A (на множестве высказываний).
Понятие УАО на множестве M. Примеры. Свойства УАО: инволютивность + закон А. де Моргана (1806-1871) в логике и теории множеств + законы исключенного третьего (Tertium non datur) и противоречия (там же).
УАО как (~5 вопросов по лекциям).
Определение. Если на некотором множестве M задан закон, по которому любому элементу a из M сопоставляется вполне определенный элемент a* из этого же множества то говорят, что на M задана унарная алгебраическая операция *.
Примеры. 1) отрицание высказываний, 2) дополнение множества до универсального, 3) центральная и осевая симметрия.
Свойства:
1) Инволютивность. УАО инволютивно, если для любого а из M выполняется равенство а*=а. Примеры. 1) U=N (U – универсальное множество). Для множества N2 его дополнением до универсального будет множество  , в свою очередь его дополнением до универсального будет
, в свою очередь его дополнением до универсального будет  , а по свойству N2=
, а по свойству N2=  . 2) 7>5,
. 2) 7>5,  ,
, 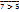 =7>5.
=7>5.
2) Закон де Моргана. Если для любых а и b из M выполняется равенство (a◦b)*=a*▫b*=a, то это закон де Моргана. Примеры. 1)  , 2)
, 2)  .
.
3) Закон исключенного третьего. Если для любых а из M выполняется равенство a◦а*=е, то это закон исключенного третьего. Примеры. 1) Аv  =И, 2) А
=И, 2) А  =U.
=U.
4) Закон противоречия. Если для любых а из M выполняется равенство a◦а*=е, то это закон противоречия. Примеры. 1) Аʌ  =Л, 2) А
=Л, 2) А  =Ø.
=Ø.
Примеры комбинаторных задач
Определение. В обыденной жизни нам не редко встречаются задачи, которые имеют несколько различных вариантов решения. Чтобы сделать правильный выбор, важно не упустить ни один из них. Для этого надо уметь осуществлять перебор всех возможных вариантов или подсчитывать их число. Задачи требующие такого решения, называют комбинаторными.
Примеры: 1) Сколько квадратов на рисунке? (всего 5)
2) Сколько здесь прямоугольников? (1×1-4, 2×1-2, 1×2-2, 2×2-1 всего 9)
3) Сколько треугольников на рисунке?



 Теорема: (для 2-х множеств) | AUB|+ |AUB|=|A|+|B|. Док-во: Если сложитьA| и |B|, то сумма будет больше | AUB| на | AUB|, т.к. эл-ты пересечения были сосчитаны дважды.
Теорема: (для 2-х множеств) | AUB|+ |AUB|=|A|+|B|. Док-во: Если сложитьA| и |B|, то сумма будет больше | AUB| на | AUB|, т.к. эл-ты пересечения были сосчитаны дважды. B|-|B
B|-|B  Доказательство:Если сложить ||A|, |B|, |C|, то сумма будет больше модуля |AUBUC| на |A
Доказательство:Если сложить ||A|, |B|, |C|, то сумма будет больше модуля |AUBUC| на |A  В 1-ом случае (рис. выше): 9,8,7,3. Во 2-м случае- что же делать?(будем писать в центре 3, а дальше 6, 5, 4). Мы заметим, что 1-ый случай не может иметь места.(условие можно понимать только как 2-ой случай). Т.о. Т.к. |E
В 1-ом случае (рис. выше): 9,8,7,3. Во 2-м случае- что же делать?(будем писать в центре 3, а дальше 6, 5, 4). Мы заметим, что 1-ый случай не может иметь места.(условие можно понимать только как 2-ой случай). Т.о. Т.к. |E  Граф соответствия f – это
Граф соответствия f – это b. Например, 1f1, но 1
b. Например, 1f1, но 1  2, 13f1, но 13
2, 13f1, но 13  2.
2. . Попробуем ввести в этом множестве отношение порядка.
. Попробуем ввести в этом множестве отношение порядка.  , если a<b – порядок.
, если a<b – порядок.  , если a и b взаимно простые числа. g – не транзитивно. Контрпример:
, если a и b взаимно простые числа. g – не транзитивно. Контрпример:  ,
,  , но
, но  .
. , в свою очередь его дополнением до универсального будет
, в свою очередь его дополнением до универсального будет  , а по свойству N2=
, а по свойству N2=  ,
, 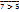 =7>5.
=7>5. , 2)
, 2)  .
. =И, 2) А
=И, 2) А  =U.
=U. =Ø.
=Ø.


