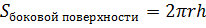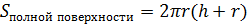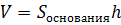Логарифмы
· Логарифм числа b по основанию a (log ab) определяется как показатель степени, в которую надо возвести число a, чтобы получить число b (Логарифм существует только у положительных чисел).
· Обозначение: log ab.
· log ab = x, ax = b.
· Логарифм числа b по основанию a - log ab (a > 0, a ≠ 1, b > 0)
· Десятичный логарифм - lg b (Логарифм по основанию 10, а = 10).
· Натуральный логарифм - ln b (Логарифм по основанию e, а = e).
Переход от выражения к логарифму называется логарифмированием этого выражения. Переход от логарифма к подлогарифмическому выражению называется потенциированием.

| ОСНОВНЫЕ СВОЙСТВА КОРНЕЙ
| ОСНОВНЫЕ СВОЙСТВА ЛОГАРИФМОВ
|
- n√a b = n√ a × n√ b
- n√a / b = n√a / n√b (b ≠ 0)
- n√ k√ a = nk√ a, (k > 0)
- n√ a = nk√ a k, (k > 0)
- n√ a k = (n√ a)k, если k ≤ 0, то a ≠ 0
- n√ x n = | x |, если n – четно и x, если n – нечетно.
- n√ – a ≤ – n√ a
- для любых a для любых b, таких что 0 ≤ a ≤ b верно неравенство: n√ a ≤ n√ a
| Для любых a; a > 0; a ≠ 1 и для любых x; y > 0.
1. loga1 = 0
- logaa = 1
- logax×y = logax + logay
- logax/y = logax – logay
- logaxp = p logax, если p – четное число, тогда | x |
- logak x = 1/k × logax, при k ≠ 0
- logax = logac xc
- logax = (logbx) / (logba)
- alogab = b (определение логарифма)
|
Правила дифференцирования общих функций

| Таблица Первообразных
| Таблица Производных
|
sinx=0, x=pn
sinx=1, x=p/2+2pn
sinx=-1, x=-p/2+2pn
cosx=0, x=p/2+pn
cosx=1, x=2pn
cosx=-1, x=p+2pn, где nÎZ

| ФОРМУЛЫ ПРИВЕДЕНИЯ
|
| Функция / угол
| π/2 – α
| π/2 + α
| π – α
| π + α
| 3π/2 – α
| 3π/2 + α
| 2π – α
| 2π + α
|
| sin
| cos α
| cos α
| sin α
| – sin α
| – cos α
| – cos α
| – sin α
| sin α
|
| cos
| sin α
| – sin α
| – cos α
| – cos α
| – sin α
| sin α
| cos α
| cos α
|
| tg
| ctg α
| – ctg α
| – tg α
| tg α
| ctg α
| – ctg α
| – tg α
| tg α
|
| ctg
| tg α
| – tg α
| – ctg α
| ctg α
| tg α
| – tg α
| – ctg α
| ctg α
|
y = f(x0) + f '(x0)(x – x0) – уравнение касательной
Стереометрия.
· В пространстве через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.
· Через три точки, не лежащие на одной прямой, всегда можно провести плоскость (и притом только одну).
· Прямая, две точки которой лежат в плоскости, вся лежит в этой плоскости (т.е. все её точки лежат в плоскости). Следовательно, если прямая не лежит в плоскости, то на не может иметь с ней более одной общей точки (точка пересечения прямой и плоскости).
· Параллельные прямые определяют плоскость и притом только одну.
· Если две прямые параллельны третей прямой, то они параллельны между собой.
· Два угла с соответственно параллельными и одинаково направленными сторонами равны.
· Прямые называются скрещивающимися, если одна из прямых лежит в плоскости, а другая эту плоскость пересекает в точке не принадлежащей первой прямой.
· Прямые называются скрещивающимися, если одна из прямых лежит в плоскости, а другая эту плоскость пересекает в точке не принадлежащей первой прямой.
· Скрещивающиеся прямые не определяют плоскость.
· Углом между скрещивающимися прямыми называется угол между двумя прямыми, параллельными им и проходящими через произвольную точку.
· Синус угла между скрещивающимися прямыми равен отношению длины проекции одной из прямых на плоскость, к которой другая прямая перпендикулярна, к её длине.
· Плоскостью называется поверхность, обладающая тем свойством, что всякая прямая, соединяющая две её точки, лежит в ней целиком.
· Прямая может занимать относительно плоскости три различных положения:
1) Она может иметь с ней две общие точки и, следовательно, лежать в ней целиком; в этом случае говорят также, что плоскость проходит через прямую.
2) Она может иметь с ней одну общую точку; в этом случае говорят, что прямая пересекает плоскость.
3) Наконец, плоскость и прямая могут не иметь ни одной общей точки; в этом случае говорят, что они параллельны.
· Через три точки, не лежащие на одной прямой, проходит только одна плоскость.
· Три точки пространства, не лежащие на одной прямой, определяют плоскость.
· Прямая и точка вне её определяют плоскость.
· Две пересекающиеся прямые определяют плоскость и притом только одну.
· Две прямые в пространстве называют параллельными, если они лежат в одной плоскости и не пересекаются.
· Две параллельные прямые определяют плоскость и притом только одну.
· Две различные плоскости, имеющие одну общую точку, имеют бесчисленное множество общих точек, образующих прямую линию.
· Если эти прямые не совпадают между собой, то могут, очевидно, иметь место лишь следующие три случая:
1) прямые пересекаются;
2) прямые параллельны;
3) прямые не лежат в одной плоскости.
· Прямая называется перпендикулярной к плоскости, если она перпендикулярна ко всем прямым, проходящим через точку её пересечения с этой плоскостью и лежащим в этой плоскости.
· Перпендикуляром, проведенным из данной точки к данной плоскости, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной данной плоскости.
· Наклонной, проведенной из данной точки к данной плоскости, называется отрезок, соединяющий данную точку с любой точкой взятой плоскости, не являющейся основанием перпендикуляра, опущенного из данной точки на данную плоскость. Один из концов наклонной, лежащий на плоскости, называется основанием наклонной.
· Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной точки, называется проекцией наклонной на плоскости (имеется ввиду данная плоскость и данная наклонная).
· Прямая, перпендикулярная к плоскости, перпендикулярна ко всем прямым, лежащим на плоскости.
· Прямая, перпендикулярная к плоскости, перпендикулярна ко всем прямым, параллельным этой плоскости.
· Если прямая перпендикулярна ко всем прямым, лежащим в некоторой плоскости, то она не может быть параллельной этой плоскости следовательно, она пересекает плоскость и потому к ней перпендикулярна.
· Плоскость, перпендикулярная к некоторой прямой, перпендикулярна ко всякой прямой, параллельной этой прямой.
· Геометрическое место точек, равноудалённых от двух точек В и B1, есть плоскость, перпендикулярная к прямой ВВ1 и проходящая через середину отрезка ВВ1.
· Для, того, чтобы какая-либо прямая, была перпендикулярна к плоскости, достаточно, чтобы она была перпендикулярна к двум прямым, лежащим в этой плоскости и проходящим через точку пересечения прямой плоскостью.
· Для того, чтобы прямая D была перпендикулярна к плоскости Р, достаточно, чтобы она была перпендикулярна к двум прямым D1 и D2, не параллельным между собой и лежащим в этой плоскости или ей параллельным.
· Через данную точку О пространства можно про вести плоскость, перпендикулярную к прямой D и притом только одну. Эта плоскость есть геометрическое место прямых, перпендикулярных к данной прямой и проходящих через данную точку.
· Две плоскости, перпендикулярные к одной и той же прямой, параллельны.
· Прямая и плоскость, перпендикулярные к одной и той же прямой, параллельны.
· Через данную точку О пространства можно провести прямую, перпендикулярную к данной плоскости Р, и притом только одну.
· Две прямые, перпендикулярные одной и той же плоскости, параллельны между собой.
· Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
· Если из точки, лежащей вне плоскости, провести к этой плоскости перпендикуляр и различные наклонные, то:
- перпендикуляр короче всякой наклонной;
- две наклонные, одинаково удалённые от основания перпендикуляра, равны;
- из двух наклонных, не одинаково удаленных от основания перпендикуляра, длиннее та, основание которой дальше отстоит от основания перпендикуляра.
· Расстоянием точки от плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость.
· Прямая и плоскость называются параллельными, если они не пересекаются.
· Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то на параллельна и самой плоскости.
· Угол между прямой лежащей в одной плоскости с другой плоскостью есть угол между этой прямой и её проекцией на эту плоскость.
· Теорема о трех перпендикулярах. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной.
· Обратная теореме о трех перпендикулярах. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и её проекции.
· Двугранным углом называется часть пространства, ограниченная двумя полуплоскостями, границей каждой из которых служит их общая прямая. Двугранный угол также называют углом между данными плоскостями.
· Плоскости (полуплоскости), которые ограничивают двугранный угол, называются гранями двугранного угла.
· Линия пересечения граней двугранного угла называется ребром двугранного угла.
· Линейным углом двугранного угла называется угол, образованный двумя полупрямыми, полученными при пересечении граней двугранного угла плоскостью, перпендикулярной ребру этого двугранного угла. Значение линейного угла данного двугранного угла есть значение данного двугранного угла.
· Две плоскости называются параллельными, если они не пересекаются, сколько бы мы их не продолжали.
· Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
· Если две параллельные плоскости пересекаются третей, то прямые пересечения параллельны.
· Отрезки параллельных прямых, заключенных между двумя параллельными плоскостями, равны.
· Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они тоже перпендикулярны.
· Две плоскости называются перпендикулярными, если линейный угол при ребре двугранного угла между этими плоскостями — прямой.
· Признак перпендикулярности плоскостей. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
· Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то это перпендикуляр полностью лежит в первой плоскости.
· Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.
Пирамида
Пирамидой называется тело, образованное плоским многоугольником (основание), точкой, не лежащей в плоскости этого многоугольника (вершина), и всех отрезков, соединяющих точки основания с вершиной. Стороны основания есть ребра основания. Прямые, соединяющие вершины основания с вершиной трапеции, есть боковые ребра. Совокупности прямых, соединяющих каждую по отдельности сторону основания с вершиной, называются боковыми гранями. Совокупность боковых граней задает боковую поверхность пирамиды. Высота, проведенная в боковой грани из вершины пирамиды на сторону основания, называется апофемой. Углы при вершине боковых граней называются плоскими углами при вершине пирамиды. Двугранные углы, образованные смежными боковым гранями, называются двугранными углами при боковых ребрах пирамиды. При вершинах основания мы имеем n трехгранных углов. Здесь: Плоские углы, образованные боковыми ребрами и сторонами основания, называются плоскими углами при основании. Двугранные углы между боковыми гранями и плоскостью основания называются двугранными углами при основании. Треугольная пирамида иначе называется тетраэдром (т.е. четырехгранником). Особенность тетраэдра в том, что любая из его граней может быть принята за основание.
Пирамида называется правильной, если в её основании лежит правильный многоугольник, а высота, опущенная из вершины пирамиды на основание, пересекает его в центре этого многоугольника (иначе говоря, вершина пирамиды проектируется в центр основания).
Прямоугольной называется пирамида, одно из боковых ребер которой перпендикулярно основанию.
A – длина апофемы
Конус
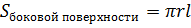

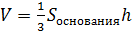 l - образующая
l - образующая
Цилиндр
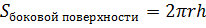
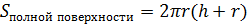
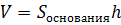
Логарифмы
· Логарифм числа b по основанию a (log ab) определяется как показатель степени, в которую надо возвести число a, чтобы получить число b (Логарифм существует только у положительных чисел).
· Обозначение: log ab.
· log ab = x, ax = b.
· Логарифм числа b по основанию a - log ab (a > 0, a ≠ 1, b > 0)
· Десятичный логарифм - lg b (Логарифм по основанию 10, а = 10).
· Натуральный логарифм - ln b (Логарифм по основанию e, а = e).
Переход от выражения к логарифму называется логарифмированием этого выражения. Переход от логарифма к подлогарифмическому выражению называется потенциированием.

| ОСНОВНЫЕ СВОЙСТВА КОРНЕЙ
| ОСНОВНЫЕ СВОЙСТВА ЛОГАРИФМОВ
|
- n√a b = n√ a × n√ b
- n√a / b = n√a / n√b (b ≠ 0)
- n√ k√ a = nk√ a, (k > 0)
- n√ a = nk√ a k, (k > 0)
- n√ a k = (n√ a)k, если k ≤ 0, то a ≠ 0
- n√ x n = | x |, если n – четно и x, если n – нечетно.
- n√ – a ≤ – n√ a
- для любых a для любых b, таких что 0 ≤ a ≤ b верно неравенство: n√ a ≤ n√ a
| Для любых a; a > 0; a ≠ 1 и для любых x; y > 0.
1. loga1 = 0
- logaa = 1
- logax×y = logax + logay
- logax/y = logax – logay
- logaxp = p logax, если p – четное число, тогда | x |
- logak x = 1/k × logax, при k ≠ 0
- logax = logac xc
- logax = (logbx) / (logba)
- alogab = b (определение логарифма)
|
Правила дифференцирования общих функций

| Таблица Первообразных
| Таблица Производных
|
sinx=0, x=pn
sinx=1, x=p/2+2pn
sinx=-1, x=-p/2+2pn
cosx=0, x=p/2+pn
cosx=1, x=2pn
cosx=-1, x=p+2pn, где nÎZ

| ФОРМУЛЫ ПРИВЕДЕНИЯ
|
| Функция / угол
| π/2 – α
| π/2 + α
| π – α
| π + α
| 3π/2 – α
| 3π/2 + α
| 2π – α
| 2π + α
|
| sin
| cos α
| cos α
| sin α
| – sin α
| – cos α
| – cos α
| – sin α
| sin α
|
| cos
| sin α
| – sin α
| – cos α
| – cos α
| – sin α
| sin α
| cos α
| cos α
|
| tg
| ctg α
| – ctg α
| – tg α
| tg α
| ctg α
| – ctg α
| – tg α
| tg α
|
| ctg
| tg α
| – tg α
| – ctg α
| ctg α
| tg α
| – tg α
| – ctg α
| ctg α
|
y = f(x0) + f '(x0)(x – x0) – уравнение касательной
Стереометрия.
· В пространстве через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.
· Через три точки, не лежащие на одной прямой, всегда можно провести плоскость (и притом только одну).
· Прямая, две точки которой лежат в плоскости, вся лежит в этой плоскости (т.е. все её точки лежат в плоскости). Следовательно, если прямая не лежит в плоскости, то на не может иметь с ней более одной общей точки (точка пересечения прямой и плоскости).
· Параллельные прямые определяют плоскость и притом только одну.
· Если две прямые параллельны третей прямой, то они параллельны между собой.
· Два угла с соответственно параллельными и одинаково направленными сторонами равны.
· Прямые называются скрещивающимися, если одна из прямых лежит в плоскости, а другая эту плоскость пересекает в точке не принадлежащей первой прямой.
· Прямые называются скрещивающимися, если одна из прямых лежит в плоскости, а другая эту плоскость пересекает в точке не принадлежащей первой прямой.
· Скрещивающиеся прямые не определяют плоскость.
· Углом между скрещивающимися прямыми называется угол между двумя прямыми, параллельными им и проходящими через произвольную точку.
· Синус угла между скрещивающимися прямыми равен отношению длины проекции одной из прямых на плоскость, к которой другая прямая перпендикулярна, к её длине.
· Плоскостью называется поверхность, обладающая тем свойством, что всякая прямая, соединяющая две её точки, лежит в ней целиком.
· Прямая может занимать относительно плоскости три различных положения:
1) Она может иметь с ней две общие точки и, следовательно, лежать в ней целиком; в этом случае говорят также, что плоскость проходит через прямую.
2) Она может иметь с ней одну общую точку; в этом случае говорят, что прямая пересекает плоскость.
3) Наконец, плоскость и прямая могут не иметь ни одной общей точки; в этом случае говорят, что они параллельны.
· Через три точки, не лежащие на одной прямой, проходит только одна плоскость.
· Три точки пространства, не лежащие на одной прямой, определяют плоскость.
· Прямая и точка вне её определяют плоскость.
· Две пересекающиеся прямые определяют плоскость и притом только одну.
· Две прямые в пространстве называют параллельными, если они лежат в одной плоскости и не пересекаются.
· Две параллельные прямые определяют плоскость и притом только одну.
· Две различные плоскости, имеющие одну общую точку, имеют бесчисленное множество общих точек, образующих прямую линию.
· Если эти прямые не совпадают между собой, то могут, очевидно, иметь место лишь следующие три случая:
1) прямые пересекаются;
2) прямые параллельны;
3) прямые не лежат в одной плоскости.
· Прямая называется перпендикулярной к плоскости, если она перпендикулярна ко всем прямым, проходящим через точку её пересечения с этой плоскостью и лежащим в этой плоскости.
· Перпендикуляром, проведенным из данной точки к данной плоскости, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной данной плоскости.
· Наклонной, проведенной из данной точки к данной плоскости, называется отрезок, соединяющий данную точку с любой точкой взятой плоскости, не являющейся основанием перпендикуляра, опущенного из данной точки на данную плоскость. Один из концов наклонной, лежащий на плоскости, называется основанием наклонной.
· Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной точки, называется проекцией наклонной на плоскости (имеется ввиду данная плоскость и данная наклонная).
· Прямая, перпендикулярная к плоскости, перпендикулярна ко всем прямым, лежащим на плоскости.
· Прямая, перпендикулярная к плоскости, перпендикулярна ко всем прямым, параллельным этой плоскости.
· Если прямая перпендикулярна ко всем прямым, лежащим в некоторой плоскости, то она не может быть параллельной этой плоскости следовательно, она пересекает плоскость и потому к ней перпендикулярна.
· Плоскость, перпендикулярная к некоторой прямой, перпендикулярна ко всякой прямой, параллельной этой прямой.
· Геометрическое место точек, равноудалённых от двух точек В и B1, есть плоскость, перпендикулярная к прямой ВВ1 и проходящая через середину отрезка ВВ1.
· Для, того, чтобы какая-либо прямая, была перпендикулярна к плоскости, достаточно, чтобы она была перпендикулярна к двум прямым, лежащим в этой плоскости и проходящим через точку пересечения прямой плоскостью.
· Для того, чтобы прямая D была перпендикулярна к плоскости Р, достаточно, чтобы она была перпендикулярна к двум прямым D1 и D2, не параллельным между собой и лежащим в этой плоскости или ей параллельным.
· Через данную точку О пространства можно про вести плоскость, перпендикулярную к прямой D и притом только одну. Эта плоскость есть геометрическое место прямых, перпендикулярных к данной прямой и проходящих через данную точку.
· Две плоскости, перпендикулярные к одной и той же прямой, параллельны.
· Прямая и плоскость, перпендикулярные к одной и той же прямой, параллельны.
· Через данную точку О пространства можно провести прямую, перпендикулярную к данной плоскости Р, и притом только одну.
· Две прямые, перпендикулярные одной и той же плоскости, параллельны между собой.
· Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
· Если из точки, лежащей вне плоскости, провести к этой плоскости перпендикуляр и различные наклонные, то:
- перпендикуляр короче всякой наклонной;
- две наклонные, одинаково удалённые от основания перпендикуляра, равны;
- из двух наклонных, не одинаково удаленных от основания перпендикуляра, длиннее та, основание которой дальше отстоит от основания перпендикуляра.
· Расстоянием точки от плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость.
· Прямая и плоскость называются параллельными, если они не пересекаются.
· Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то на параллельна и самой плоскости.
· Угол между прямой лежащей в одной плоскости с другой плоскостью есть угол между этой прямой и её проекцией на эту плоскость.
· Теорема о трех перпендикулярах. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной.
· Обратная теореме о трех перпендикулярах. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и её проекции.
· Двугранным углом называется часть пространства, ограниченная двумя полуплоскостями, границей каждой из которых служит их общая прямая. Двугранный угол также называют углом между данными плоскостями.
· Плоскости (полуплоскости), которые ограничивают двугранный угол, называются гранями двугранного угла.
· Линия пересечения граней двугранного угла называется ребром двугранного угла.
· Линейным углом двугранного угла называется угол, образованный двумя полупрямыми, полученными при пересечении граней двугранного угла плоскостью, перпендикулярной ребру этого двугранного угла. Значение линейного угла данного двугранного угла есть значение данного двугранного угла.
· Две плоскости называются параллельными, если они не пересекаются, сколько бы мы их не продолжали.
· Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
· Если две параллельные плоскости пересекаются третей, то прямые пересечения параллельны.
· Отрезки параллельных прямых, заключенных между двумя параллельными плоскостями, равны.
· Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они тоже перпендикулярны.
· Две плоскости называются перпендикулярными, если линейный угол при ребре двугранного угла между этими плоскостями — прямой.
· Признак перпендикулярности плоскостей. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
· Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то это перпендикуляр полностью лежит в первой плоскости.
· Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.
Пирамида
Пирамидой называется тело, образованное плоским многоугольником (основание), точкой, не лежащей в плоскости этого многоугольника (вершина), и всех отрезков, соединяющих точки основания с вершиной. Стороны основания есть ребра основания. Прямые, соединяющие вершины основания с вершиной трапеции, есть боковые ребра. Совокупности прямых, соединяющих каждую по отдельности сторону основания с вершиной, называются боковыми гранями. Совокупность боковых граней задает боковую поверхность пирамиды. Высота, проведенная в боковой грани из вершины пирамиды на сторону основания, называется апофемой. Углы при вершине боковых граней называются плоскими углами при вершине пирамиды. Двугранные углы, образованные смежными боковым гранями, называются двугранными углами при боковых ребрах пирамиды. При в





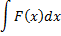
 Интегрирование
Интегрирование

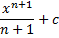
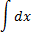
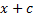

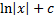
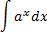
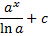

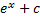

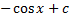
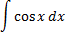

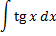
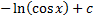
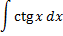

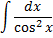

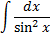
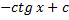
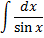
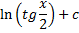

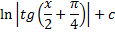
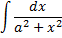

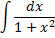

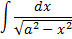
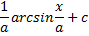
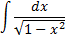

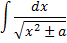

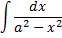
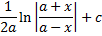
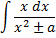


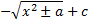
 Дефферинцирование
Дефферинцирование


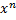
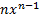
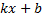
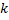
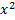
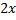
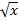
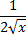



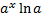
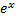



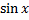



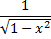

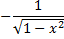
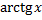
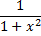


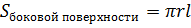

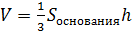 l - образующая
l - образующая