Пусть задана дифференцируемая функция 2-х переменных z=z(x,y). Дифференцируемость означает существование у нее частных производных. Эти производные в свою очередь являются функциями x, y; если они дифференцируемы, то у них тоже есть частные производные, это будут производные 2-ого порядка, т.е.

В свою очередь эти производные снова можно дифференцировать, получим производные 3-ого порядка и т.д.
Справедлива теорема Шварца:
Смешанные производные не зависят от порядка их дифференцирования, т.е.

Пример. Рассмотрим функцию  И найдем обе смешанные производные.
И найдем обе смешанные производные.
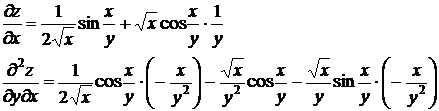
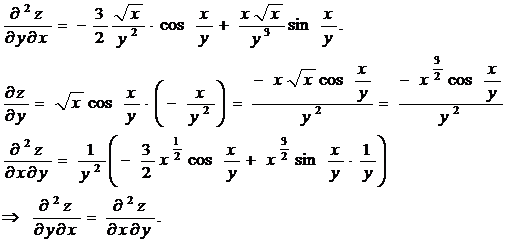
Дифференциал 2-ого порядка определяется, как дифференциал от первого дифференциала, т.е.

Символически формула для определения дифференциалов высших порядков можно записать так 
- Дать определение скалярного поля, поверхностей уровня и производной по направлению. Примеры.
Опр. Если каждой точке  поставлено в соответствие единственное число u=u(M), то говорят, что в этой области задано скалярное поле. Пример поле температур.
поставлено в соответствие единственное число u=u(M), то говорят, что в этой области задано скалярное поле. Пример поле температур.

Если в область D поместить систему координат, то скалярное поле будет задаваться функцией 3-х переменных.
Поле называется плоским, если область D занимает часть плоскости.

Поверхностью уровня скалярного поля называется поверхность, на которой скалярное поле принимает одно и то же значение: F(x,y,z)=C.
Для плоского поля линия уровня F(x,y)=C.
Градиентом с калярного поля называется вектор

Пусть скалярное поле задано двумя точками M и N, 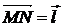 . Производная скалярного поля по направлению
. Производная скалярного поля по направлению  в точке M называется
в точке M называется

Геометрический смысл производной по направлению и частных производных.
Пусть имеется плоское поле u=f(x,y). Выберем на поверхности некоторую точку M и некоторый вектор  . Рассечем поверхность вертикальной плоскостью, проходящей через точку M и вектор
. Рассечем поверхность вертикальной плоскостью, проходящей через точку M и вектор  .
.


Если секущая плоскость параллельна оси OX, то  совпадает с частной производной по x. Можно показать, что производная по направлению вычисляется по следующей формуле: (12)
совпадает с частной производной по x. Можно показать, что производная по направлению вычисляется по следующей формуле: (12)  , где
, где  это углы, которые составляет вектор
это углы, которые составляет вектор  с осями координат или иначе вектор
с осями координат или иначе вектор 
 ортвектор вектора
ортвектор вектора 

- Доказать теорему о вычислении производной по направлению.
Если секущая плоскость параллельна оси OX, то  совпадает с частной производной по x. Можно показать, что производная по направлению вычисляется по следующей формуле:
совпадает с частной производной по x. Можно показать, что производная по направлению вычисляется по следующей формуле:

(12)  , где
, где  это углы, которые составляет вектор
это углы, которые составляет вектор  с осями координат или иначе вектор
с осями координат или иначе вектор 
 ортвектор вектора
ортвектор вектора 

Пример. 
Найти производную функции и в точке M по направлению вектора  .
.


Если поле плоское, то вектор 

(13) 
Используя формулу для градиентов формулу (12) можно записать:
 или иначе
или иначе 
Максимальное значение производной по направлению достигается, когда это направление совпадает с направлением градиента, т.е. 
- Дать определение градиента скалярного поля и доказать теорему о связи производной по направлению и градиента. Дать инвариантное определение градиента. Примеры.
Градиентом с калярного поля называется вектор

Пусть имеется плоское поле u=f(x,y). Выберем на поверхности некоторую точку M и некоторый вектор  . Рассечем поверхность вертикальной плоскостью, проходящей через точку M и вектор
. Рассечем поверхность вертикальной плоскостью, проходящей через точку M и вектор  .
.

Если секущая плоскость параллельна оси OX, то  совпадает с частной производной по x. Можно показать, что производная по направлению вычисляется по следующей формуле:
совпадает с частной производной по x. Можно показать, что производная по направлению вычисляется по следующей формуле:

(12)  , где
, где  это углы, которые составляет вектор
это углы, которые составляет вектор  с осями координат или иначе вектор
с осями координат или иначе вектор 
 ортвектор вектора
ортвектор вектора 

- Дать определение касательной плоскости и вывести уравнения касательной плоскости и нормали к поверхности. Примеры.
Пусть поверхность задана уравнениям f(x,y,z)=0. Выберем на этой поверхности некоторую точку M и проведем через эту точку различные вертикальные плоскости, в сечении получатся некоторые плоские кривые. Оказывается, что если градиент  , то касательные к этим кривым расположены в одной плоскости. Эта плоскость называется касательной плоскостью поверхности F(x,y,z)=0 в точке M.
, то касательные к этим кривым расположены в одной плоскости. Эта плоскость называется касательной плоскостью поверхности F(x,y,z)=0 в точке M.
Выведем уравнение касательной к плоскости в точке 

Нормаль к касательной плоскости совпадает с направлением градиента в этой плоскостит.
F(x,y,z)=C



Пусть поверхность задана явно z=z(x,y).
F(x,y,z)=z(x,y)-z 
- Дать определение локального экстремума функции двух переменных. Доказать теорему о необходимом условии экстремума.
Экстремум функции 2-х переменных.
z=z(x,y) в точке M0 локальный max
1) z(M) определена в окрестности  ; 2)
; 2) 

Теорема 1. Необходимое условие экстремума.
Если M0 является точкой экстремума функции т. extremum z=z(x,y), то частные производные в этой точке равны нулю. 
Пусть точка M0 – точка максимума. Проведя сечения координатными плоскостями, мы получим плоские кривые.

А для плоских линий, т.е. графика функции одной переменной необходимым условием экстремума является равенство нулю производной.
Эти производные будут частными производными для функции 2-х переменных, т.е. теорема доказана.
Опр. Точка M0 называется стационарной точкой, если частные производные в этой точке равны нулю 
Замечание.
Теорема 1 дает лишь необходимое условие экстремума, т.е. если функция дифференцируема и у нее есть экстремум, то частные производные равны нулю. Обратное вообще говоря не верно.
Замечания:
1) Функция z=z(x,y) может быть не дифференцируемой в точке M0, тем не менее экстремум там может быть.

2) Рассмотрим примеры 2-х функций:






Точка O не является точкой экстремума, O – точка минимакса.
Этот пример подчеркивает, что теорема (1) дает лишь необходимое условие экстремума.
Тем не менее в большинстве случаев определив с помощью теоремы 1 стационарные точки, догадаться о том будут ли они точками
экстремума можно исходя из геометрических или физических соображений.
- Доказать теорему о достаточном условии экстремума функции двух переменных. Примеры.
Теорема 2. Достаточное условие экстремума функции 2-х переменных.
Пусть функция z=z(x,y) дважды непрерывно дифференцируема и P0 – стационарная точка, т.е. 
Рассмотрим число
(1) 
Если  точка экстремума.
точка экстремума.
При этом если  , то
, то  точка максимума.
точка максимума.
Если  точка минимакса.
точка минимакса.
Если  , то неизвестно что это за точка.
, то неизвестно что это за точка.
Для доказательства воспользуемся формулой Тейлора:

Этот же вид формула Тейлора сохраняет для функции любого числа переменных, т.е.  , но здесь
, но здесь  ,
,

Если функция z(x,y) имеет в точке P0 экстремум, то приращение функции в окрестности этой точки сохраняет знак.

Пусть для удобства  , но в точке P0 dz=0
, но в точке P0 dz=0  знак
знак  определяется вторым дифференциалом, т.е.
определяется вторым дифференциалом, т.е.

Дальнейшие слагаемые имеют более высокий порядок малости по сравнению со вторым дифференциалом и потому знак  влияния не оказывает.
влияния не оказывает.

Получим 
В квадратных скобках стоит квадратный трехчлен по t, т.е. выражение вида
 чтобы этот трехчлен держал знак нужно, чтобы его дискриминант был отрицательным, т.е
чтобы этот трехчлен держал знак нужно, чтобы его дискриминант был отрицательным, т.е 
А это и есть условие (1) теоремы.


Если  , то P0 –точка минимума.
, то P0 –точка минимума.
Если  , то P0 – точка максимума
, то P0 – точка максимума
- Дать определение условного экстремума и рассказать о методе множителей Лагранжа. Рассказать о нахождении наибольшего и наименьшего значений функции двух переменных в области. Примеры.
Условный экстремум.
Рассмотрим следующую задачу:
Дано А квадратных сантиметров жести. Требуется сделать коробку в виде прямоугольного параллелепипеда, имеющего максимальный объем.

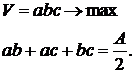



 Найти экстремум функции
Найти экстремум функции 
при выполнении условия F(x,y)=0 (2).

Задачу (1)-(2) можно попытаться решить формально, выразив из (2) уравнения y=y(x) и подставив его в (1):
 .
.
Задача нахождения условного экстремума функции (1) при условии (2) свелась к задаче нахождения безусловного экстремума функции  , однако этот путь далеко не всегда возможен, т.к. не всегда можно выразить y явно из соотношения (2), поэтому применяется другой общий прием, носящий название метод множителей Лагранжа
, однако этот путь далеко не всегда возможен, т.к. не всегда можно выразить y явно из соотношения (2), поэтому применяется другой общий прием, носящий название метод множителей Лагранжа

Ее безусловный экстремум и будет условным экстремумом функции (1) при условии (2).
Необходимым условием экстремума функции 3-х переменных является равенство нулю всех ее частных производных.

Докажем, что система (3) определяет стационарные точки для условного экстремума, для этого найдем полную производную функции  и приравняем ее к нулю
и приравняем ее к нулю

Отсюда, 
С другой стороны из соотношения (2) мы можем найти значение производной неявной функции  Эти соотношения равны, отсюда получим
Эти соотношения равны, отсюда получим
 а это и есть соотношение (3).
а это и есть соотношение (3).
Этот метод применим для функций любого числа переменных, разница лишь в том, что там возникает несколько множителей Лагранжа. Число множителей Лагранжа равно числу условий, налагаемых на функцию.
Пример.

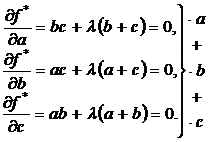
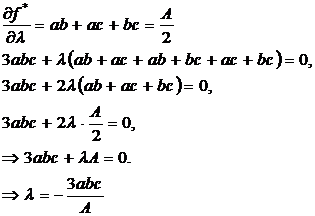
Вставляем полученное значение  вставляем в первое уравнение:
вставляем в первое уравнение:

В силу симметричности системы числа a,b и c равны между собой.

 этот параллелепипед является кубом.
этот параллелепипед является кубом.
Наименьшее и наибольшее значение функции в области (глобальный экстремум).
Пусть требуется найти экстремум некоторой функции 2-х переменных:
Z=f(x,y) в D 1) Ищем стационарные точки функции: 
Пусть это будут точки 
2) Выделяем те из них, которые находятся внутри области D и на ее границах.
Пусть это будут точки 
3) Находим значение функции в этих точках

4) Находим условный экстремум функции z при условии, что точка лежит на одной из линий, составляющих границу области D.
5) Находим значения функции в угловых точках
z(A), z(B), z(C).
Наименьшее из этих значений и будет наименьшим значением функции в области, наибольшее – наибольшим.
Пример. Найти экстремум функции  в области D, ограниченной линией
в области D, ограниченной линией 


На линии OA: y=0,z=0.
На линии OB: x=0,z=0.
На линии AB: 
т.е. 



- Дать определение первообразной и неопределенного интеграла. Доказать лемму о первообразных. Примеры.
Функция F(x) называется первообразной функции f(x), если 
Пример.

Неопределенное интегрирование – это операция, обратная дифференцированию и как всякая обратная операция она и сложнее и не всегда исполнима.
Лемма о первообразной.
Пусть  и
и  первообразные функции f(x), т.е.
первообразные функции f(x), т.е.  и
и  тогда
тогда 
Тогда они отличаются между собой не более чем на постоянную.
Доказательство:
Рассмотрим функцию  и применим к этой функции теорему Лагранжа на
и применим к этой функции теорему Лагранжа на 

Найдем чему равняется 

Эта лемма позволяет сделать корректным следующее определение:
Опр. 2. Неопределенным интегралом называется совокупность всех первообразных, т.е. справедлива формула (2)
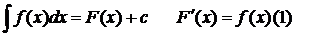
- Доказать основные свойства неопределенного интеграла и вывести правила интегрирования. Примеры.
Свойства неопределенных интегралов.
1) 
Доказательство:
Продифференцируем формулу (2)
 что и требовалось доказать.
что и требовалось доказать.
2) 
Доказательство:



3) 
1 и 2 свойства выражают взаимную обратимость операции дифференцирования и интегрирования, 3 свойство выражает линейность операции интегрирования.
На практике для вычисления интегралов их сводят к одному или нескольким табличным, используя правила интегрирования.
Пример.

Произвольная постоянная «спрятана» в последнем не взятом интеграле.
Для проверки правильности интегрирования нужно продифференцировать ответ, должна получиться подынтегральная функция.

- Инвариантность формул интегрирования. Замена переменной и интегрирование по частям в неопределенном интеграле. Примеры.
Свойство инвариантности формул интегрирования заключается в следующем: в качестве и в формулах интегрирования может стоять как независимая переменная, так и произвольная дифференцируемая функция u=u(x).





 И найдем обе смешанные производные.
И найдем обе смешанные производные.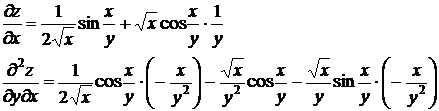
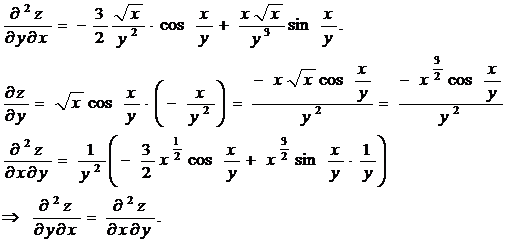


 поставлено в соответствие единственное число u=u(M), то говорят, что в этой области задано скалярное поле. Пример поле температур.
поставлено в соответствие единственное число u=u(M), то говорят, что в этой области задано скалярное поле. Пример поле температур.



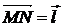 . Производная скалярного поля по направлению
. Производная скалярного поля по направлению  в точке M называется
в точке M называется


 совпадает с частной производной по x. Можно показать, что производная по направлению вычисляется по следующей формуле: (12)
совпадает с частной производной по x. Можно показать, что производная по направлению вычисляется по следующей формуле: (12)  , где
, где  это углы, которые составляет вектор
это углы, которые составляет вектор 
 ортвектор вектора
ортвектор вектора 

 .
.




 или иначе
или иначе 


 , то касательные к этим кривым расположены в одной плоскости. Эта плоскость называется касательной плоскостью поверхности F(x,y,z)=0 в точке M.
, то касательные к этим кривым расположены в одной плоскости. Эта плоскость называется касательной плоскостью поверхности F(x,y,z)=0 в точке M.





 ; 2)
; 2) 













 точка экстремума.
точка экстремума. , то
, то  точка максимума.
точка максимума. точка минимакса.
точка минимакса. , то неизвестно что это за точка.
, то неизвестно что это за точка.
 , но здесь
, но здесь  ,
,

 , но в точке P0 dz=0
, но в точке P0 dz=0  знак
знак  определяется вторым дифференциалом, т.е.
определяется вторым дифференциалом, т.е.


 чтобы этот трехчлен держал знак нужно, чтобы его дискриминант был отрицательным, т.е
чтобы этот трехчлен держал знак нужно, чтобы его дискриминант был отрицательным, т.е 


 , то P0 – точка максимума
, то P0 – точка максимума
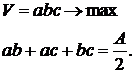



 .
. , однако этот путь далеко не всегда возможен, т.к. не всегда можно выразить y явно из соотношения (2), поэтому применяется другой общий прием, носящий название метод множителей Лагранжа
, однако этот путь далеко не всегда возможен, т.к. не всегда можно выразить y явно из соотношения (2), поэтому применяется другой общий прием, носящий название метод множителей Лагранжа



 Эти соотношения равны, отсюда получим
Эти соотношения равны, отсюда получим а это и есть соотношение (3).
а это и есть соотношение (3).
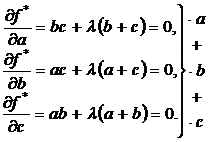
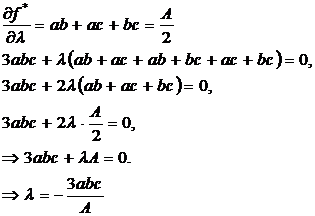
 вставляем в первое уравнение:
вставляем в первое уравнение:





 в области D, ограниченной линией
в области D, ограниченной линией 









 первообразные функции f(x), т.е.
первообразные функции f(x), т.е.  и
и  тогда
тогда 
 и применим к этой функции теорему Лагранжа на
и применим к этой функции теорему Лагранжа на 



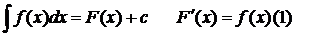

 что и требовалось доказать.
что и требовалось доказать.









