Определение. Подобием  называется такое преобразование пространства, при котором для любых точек пространства X, Y и их образов X´, Y´ выполняется соотношение
называется такое преобразование пространства, при котором для любых точек пространства X, Y и их образов X´, Y´ выполняется соотношение  , где k – некоторое фиксированное положительное число (называемое коэффициентом подобия).
, где k – некоторое фиксированное положительное число (называемое коэффициентом подобия).
Определение. Фигура Ф называется подобной фигуре Ф´, если существует подобие, переводящее Ф в Ф´.
Гомотетия пространства.
Вначале рассмотрим важный частный случай подобия – гомотетию.
Определение. Гомотетией  с центром О и коэффициентом
с центром О и коэффициентом 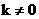 называется преобразование пространства, при котором образом каждой точки Х является точка Х´ такая, что
называется преобразование пространства, при котором образом каждой точки Х является точка Х´ такая, что  .
.
Свойства гомотетии.
- Преобразование, обратное гомотетии
 , – гомотетия
, – гомотетия  .
. - Композицией гомотетий
 и
и  является гомотетия
является гомотетия  .
. - Композицией гомотетий
 и
и 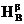 будет параллельный перенос, если
будет параллельный перенос, если 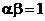 , и гомотетия с центром на прямой АВ и коэффициентом
, и гомотетия с центром на прямой АВ и коэффициентом  , если
, если  .
. - Гомотетия переводит прямую (плоскость), не проходящую через центр гомотетии, в параллельную ей прямую (плоскость); прямую (плоскость), проходящую через центр гомотетии, – в себя.
- Гомотетия сохраняет величину угла между прямыми, между прямой и плоскостью, между двумя плоскостями.
Доказательства свойств.
1 и 2. Следуют из определения гомотетии.
3. Доказывается аналогично соответствующей теореме на плоскости. Действительно, если мы рассмотрим произвольную точку Х пространства, нам будет достаточно доказать нашу теорему для плоскости (АХВ).
4. Доказывается от противного.
- Следует из свойства 1.
Свойства подобия.
Теорема 2.1. Подобие  пространства можно представить композицией гомотетии
пространства можно представить композицией гомотетии  и движения f:
и движения f:
 или
или 
Доказательство. Произведём гомотетию  с центром в произвольной точке. Рассмотрим преобразование f такое, что
с центром в произвольной точке. Рассмотрим преобразование f такое, что  (существование такого преобразования следует из определения преобразования). Преобразование f будет движением по определению движения.
(существование такого преобразования следует из определения преобразования). Преобразование f будет движением по определению движения.
Заметим, что, выбрав за f движение  , мы сможем получить представление нашего подобия и в таком виде
, мы сможем получить представление нашего подобия и в таком виде  .
.
Свойства подобия.
- При подобии прямая отображается на прямую, луч – на луч, отрезок – на отрезок, плоскость – на плоскость, полуплоскость – на полуплоскость.
- Подобие сохраняет величину угла между прямыми, между прямой и плоскостью, между плоскостями.
- Подобие сохраняет отношение отрезков.
- Если тело Т´ – образ тела Т при подобии
 , то V(T´)=k3∙V(T).
, то V(T´)=k3∙V(T).
Доказательства свойств.
1 и 2. Следствия из теоремы 2.1.
3. Следует из определения подобия.
4. Для куба теорема, очевидно, верна. Для тела, состоящего из кубов, естественно, тоже.
Произвольный многогранник М можно наложить на кубическую решётку. Будем измельчать эту решётку. При стремлении стороны одного кубика нашей решётки к нулю объёмы двух тел: тела I, состоящего из кубиков лежащих полностью внутри М, и тела S, состоящего из кубиков, имеющих общие точки с М, – стремятся к объёму многогранника М (это следует из того, что для каждой грани нашего многогранника М к нулю будет стремиться объём кубиков, пересекающих эту грань). При этом для образа М´ многогранника М при нашем подобии объёмы тел I´, S´ (образов тел I, S) стремятся к объёму многогранника М´. Для тел I и S наша теорема верна, значит, она верна и для многогранника М.
Объём произвольного тела определяется через объёмы соответствующих многогранников, поэтому теорема верна и для произвольного тела.
Теорема 2.2. (о задании подобия пространства) Если даны два тетраэдра ABCD и A´B´C´D´ такие, что  , то существует ровно одно подобие пространства, при котором А→А´, В→В´, С→С´, D→D´.
, то существует ровно одно подобие пространства, при котором А→А´, В→В´, С→С´, D→D´.
Доказательство. То, что такое подобие существует, следует из теоремы 2.1 и теоремы о задании движения пространства (часть I, теорема 5.1). Пусть таких преобразований два: P и Р´. Тогда преобразование 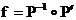 – движение, имеющие неподвижные точки A, B, C, D, т.е. f – тождественное преобразование. Отсюда Р=Р´.
– движение, имеющие неподвижные точки A, B, C, D, т.е. f – тождественное преобразование. Отсюда Р=Р´.



 называется такое преобразование пространства, при котором для любых точек пространства X, Y и их образов X´, Y´ выполняется соотношение
называется такое преобразование пространства, при котором для любых точек пространства X, Y и их образов X´, Y´ выполняется соотношение  , где k – некоторое фиксированное положительное число (называемое коэффициентом подобия).
, где k – некоторое фиксированное положительное число (называемое коэффициентом подобия). с центром О и коэффициентом
с центром О и коэффициентом 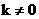 называется преобразование пространства, при котором образом каждой точки Х является точка Х´ такая, что
называется преобразование пространства, при котором образом каждой точки Х является точка Х´ такая, что  .
. .
. и
и  является гомотетия
является гомотетия  .
. и
и 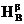 будет параллельный перенос, если
будет параллельный перенос, если 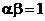 , и гомотетия с центром на прямой АВ и коэффициентом
, и гомотетия с центром на прямой АВ и коэффициентом  , если
, если  .
. и движения f:
и движения f: или
или 
 , мы сможем получить представление нашего подобия и в таком виде
, мы сможем получить представление нашего подобия и в таком виде  , то существует ровно одно подобие пространства, при котором А→А´, В→В´, С→С´, D→D´.
, то существует ровно одно подобие пространства, при котором А→А´, В→В´, С→С´, D→D´.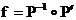 – движение, имеющие неподвижные точки A, B, C, D, т.е. f – тождественное преобразование. Отсюда Р=Р´.
– движение, имеющие неподвижные точки A, B, C, D, т.е. f – тождественное преобразование. Отсюда Р=Р´.


