Часть I. Движения пространства.

Введение.

Геометрические преобразования являются достаточно поздним разделом математики. Первые геометрические преобразования стали рассматриваться в XVII веке, а проективные преобразования появились лишь в начале XIX века.

В алгебре рассматриваются различные функции. Функция f каждому числу х из области определения функции ставит в соответствие некоторое число f(x) – значение функции f в точке х. В геометрии рассматриваются функции, у которых другие области определения и множества значений. Они каждой точке ставят в соответствие точку. Эти функции называются геометрическими преобразованиями.

Геометрические преобразования имеют большое значение в геометрии. С помощью геометрических преобразований определяются такие важные геометрические понятия, как равенство и подобие фигур. Благодаря геометрическим преобразованиям, многие разрозненные факты геометрии укладываются в стройную теорию.

В реферате, в основном, речь пойдёт о преобразованиях пространства. Будут рассмотрены все движения, подобия, круговые и аффинные преобразования пространства, а также аффинные и проективные преобразования плоскости. Для каждого преобразования будут рассмотрены его свойства и примеры применения к решению геометрических задач.

Для начала обратимся к некоторым основным понятиям, которые будут необходимы нам для работы с преобразованиями. Остановимся на двух терминах: расстояние и преобразование. Итак, что мы будем понимать под этими словами:

 

Определение. Расстоянием между двумя точками будем называть длину отрезка с концами в этих точках.

 

Определение. Преобразованием множества будем называть взаимно однозначное отображение этого множества на себя.

 

Теперь перейдём к рассмотрению отдельных видов геометрических преобразований.

Часть I. Движения пространства.

Общие свойства движений.

Определение. Преобразование пространства называется движением, если оно сохраняет расстояния между точками.

Свойства движений.

1. Преобразование, обратное к движению, – движение.
2. Композиция движений – движение.
3. При движении прямая переходит в прямую, луч – в луч, отрезок – в отрезок, плоскость – в плоскость, полуплоскость – в полуплоскость.
4. Образом плоского угла при движении является плоский угол той же величины.
5. Движение сохраняет величину угла между прямыми, между прямой и плоскостью, между плоскостями.
6. Движение сохраняет параллельность прямых, прямой и плоскости, плоскостей.

 

Доказательства свойств.

1 и 2. Следуют из определения движения.

1. Пусть точки А, Х и В лежат на одной прямой, причём точка Х лежит между А и В. Тогда АХ+ХВ=АВ. Пусть точки А´, Х´, В´ – образы точек А, Х, В при движении. Тогда А´Х´+Х´В´=А´В´ (из определения движения). А отсюда следует, что точки A´, X´, B´ лежат на одной прямой, причём Х´ лежит между А´ и В´.
   Из доказанного утверждения сразу следует, что при движении прямая переходит в прямую, луч – в луч, отрезок – в отрезок.

Для плоскости доказательство можно провести так. Пусть a, b – две пересекающиеся прямые нашей плоскости α, a´, b´ – их образы. Очевидно, a´ и b´ пересекаются. Пусть α´ – плоскость, содержащая прямые a´, b´. Докажем, что α´ – образ плоскости α. Пусть М – произвольная точка плоскости α, не лежащая на прямых a и b. Проведём через M прямую c, пересекающую прямые a и b в различных точках. Образом этой прямой является прямая с´, пересекающая прямые a´, b´ в различных точках. Значит, 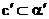и М´, образ точки М, лежит в плоскости α´. Итак, образ любой точки плоскости α лежит в плоскости α´. Аналогично доказывается, что прообраз любой точки плоскости α´ лежит в плоскости α. Отсюда α´ – образ плоскости α.

Теперь уже несложно доказать утверждение и для полуплоскости. Надо лишь дополнить полуплоскость до плоскости, рассмотреть прямую а, ограничивающую полуплоскость, и её образ а´, а затем доказать от противного, что образы любых двух точек полуплоскости лежат по одну сторону от а´.

1. Следует из свойства 3.
2. Следует из свойства 4 и определения угла между прямыми (прямой и плоскостью, двумя плоскостями) в пространстве.
3. Предположим противное, т.е. пусть образы наших параллельных прямых (прямой и плоскости, плоскостей) пересекаются (в случае параллельных прямых ещё надо показать, что их образы не могут быть скрещивающимися прямыми, но это сразу следует из того, что плоскость, содержащая эти прямые, перейдёт в плоскость). Тогда рассмотрим их общую точку. У неё будет два прообраза, что невозможно по определению преобразования.

 

Определение. Фигура Ф называется равной фигуре Ф´, если существует движение, переводящее Ф в Ф´.

 

Виды движений.

3.1. Тождественное преобразование.

Определение. Тождественным преобразованием Е пространства называется преобразование, при котором каждая точка пространства переходит в себя.

Очевидно, тождественное преобразование является движением.

3.2. Параллельный перенос.

Определение. Пусть в пространстве задан вектор . Параллельным переносом пространства на вектор называется преобразование, при котором каждая точка М отображается в такую точку М´, что .

Теорема 3.2. Параллельный перенос – движение.

Доказательство. Пусть А´, В´ – образы точек А, В при параллельном переносе на вектор . Достаточно показать, что АВ=А´В´, что следует из равенства:

.

 

Свойство переноса. Параллельный перенос переводит прямую (плоскость) в себя или в параллельную ей прямую (плоскость).

 

Доказательство. При доказательстве теоремы 3.2, мы доказали, что при параллельном переносе сохраняются вектора. Значит, сохраняются направляющие вектора прямых и векторы нормали плоскостей. Отсюда и следует наше утверждение.

 

Центральная симметрия.

Определение. Симметрией 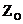относительно точки О (центральной симметрией) пространства называется преобразование пространства, которое точку О отображает на себя, а любую другую точку М отображает на такую точку М´, что точка О является серединой отрезка ММ´. Точка О называется центром симметрии.

 

Теорема 3.4. Центральная симметрия – движение.

 

Доказательство.

Пусть А, В – две произвольные точки, А´, В´ – их образы, О – центр симметрии. Тогда .

 

Свойство центральной симметрии. Центральная симметрия переводит прямую (плоскость) в себя или в параллельную ей прямую (плоскость).

 

Доказательство. При доказательстве теоремы 3.4, мы доказали, что при параллельном переносе вектора меняются на противоположные. Значит, у направляющих векторов прямых и векторов нормали плоскостей при центральной симметрии лишь меняются направления. Отсюда и следует наше утверждение.

Теорема о задании движения.

Теорема 5.1. (теорема о задании движения) Если даны два тетраэдра ABCD и A´B´C´D´ с соответственно равными рёбрами, то существует одно и только одно движение пространства, отображающее точки A, B, C, D соответственно на точки A´, B´, C´, D´.

Доказательство.

I. Существование. Если А совпадает с А´, В – с B´, С – с C´, D – с D´, то задано просто тождественное преобразование. Если нет, то положим для определённости, что А не совпадает с А´. Рассмотрим плоскость α симметрии точек А и А´. Пусть симметрия S_α переводит тетраэдр ABCD в тетраэдр A´B₁C₁D₁.

Теперь, если В₁ совпала с В´, С₁ – с С´, D₁ – с D´, то доказательство завершено. Если нет, то можно без ограничения общности считать, что точки В´ и В₁ не совпали. Рассмотрим плоскость β симметрии точек B₁ и B´. Точка A´ – равноудалена от точек В₁ и В´, следовательно лежит на плоскости β. Пусть симметрия S_β переводит тетраэдр A´B₁C₁D₁ в тетраэдр A´B´C₂D₂.

Теперь, если С₂ совпала с С´, а D₂ – с D´, то доказательство завершено. Если нет, то можно без ограничения общности считать, что точки С´ и С₂ не совпали. Рассмотрим плоскость γ симметрии точек С₂ и С´. Точки А´, В´ равноудалены от точек С₂ и С´, поэтому лежат в плоскости γ. Пусть симметрия S_γ переводит тетраэдр A´B´C₂D₂ в тетраэдр A´B´C´D₃.

Теперь, если D₃ совпала с D´, то доказательство завершено. Если нет, то рассмотрим плоскость δ симметрии точек D₃ и D´. Точки А´, В´, С´ равноудалены от точек D₃ и D´, поэтому лежат в плоскости δ. Значит, симметрия S_δ переводит тетраэдр A´B´C´D₃ в тетраэдр A´B´C´D´.

Итак, композиция нужного числа приведённых зеркальных симметрий переводит тетраэдр ABCD в тетраэдр A´B´C´D´. А это преобразование является движением (свойство 2 движений).

II. Единственность. Пусть существуют 2 движения f и g, переводящие А в А´, В в В´, С в С´, D в D´. Тогда движение является тождественным преобразованием, т.к. оставляет точки А, B, C, D неподвижными. Значит, f=g.

 

При доказательстве теоремы 5.1 (существование), фактически была доказана и

Теорема 5.2. Любое движение пространства есть композиция не более четырёх зеркальных симметрий.

Гомотетия пространства.

Вначале рассмотрим важный частный случай подобия – гомотетию.

Определение. Гомотетией с центром О и коэффициентом 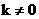называется преобразование пространства, при котором образом каждой точки Х является точка Х´ такая, что .

 

Свойства гомотетии.

1. Преобразование, обратное гомотетии , – гомотетия .
2. Композицией гомотетий и является гомотетия .
3. Композицией гомотетий и 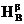будет параллельный перенос, если 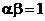, и гомотетия с центром на прямой АВ и коэффициентом , если .
4. Гомотетия переводит прямую (плоскость), не проходящую через центр гомотетии, в параллельную ей прямую (плоскость); прямую (плоскость), проходящую через центр гомотетии, – в себя.
5. Гомотетия сохраняет величину угла между прямыми, между прямой и плоскостью, между двумя плоскостями.

 

Доказательства свойств.

1 и 2. Следуют из определения гомотетии.

3. Доказывается аналогично соответствующей теореме на плоскости. Действительно, если мы рассмотрим произвольную точку Х пространства, нам будет достаточно доказать нашу теорему для плоскости (АХВ).

4. Доказывается от противного.

1. Следует из свойства 1.

 

Свойства подобия.

 

Теорема 2.1. Подобие пространства можно представить композицией гомотетии и движения f:

или

 

Доказательство. Произведём гомотетию с центром в произвольной точке. Рассмотрим преобразование f такое, что (существование такого преобразования следует из определения преобразования). Преобразование f будет движением по определению движения.

Заметим, что, выбрав за f движение , мы сможем получить представление нашего подобия и в таком виде .

 

Свойства подобия.

1. При подобии прямая отображается на прямую, луч – на луч, отрезок – на отрезок, плоскость – на плоскость, полуплоскость – на полуплоскость.
2. Подобие сохраняет величину угла между прямыми, между прямой и плоскостью, между плоскостями.
3. Подобие сохраняет отношение отрезков.
4. Если тело Т´ – образ тела Т при подобии , то V(T´)=k³∙V(T).

 

Доказательства свойств.

1 и 2. Следствия из теоремы 2.1.

3. Следует из определения подобия.

4. Для куба теорема, очевидно, верна. Для тела, состоящего из кубов, естественно, тоже.

Произвольный многогранник М можно наложить на кубическую решётку. Будем измельчать эту решётку. При стремлении стороны одного кубика нашей решётки к нулю объёмы двух тел: тела I, состоящего из кубиков лежащих полностью внутри М, и тела S, состоящего из кубиков, имеющих общие точки с М, – стремятся к объёму многогранника М (это следует из того, что для каждой грани нашего многогранника М к нулю будет стремиться объём кубиков, пересекающих эту грань). При этом для образа М´ многогранника М при нашем подобии объёмы тел I´, S´ (образов тел I, S) стремятся к объёму многогранника М´. Для тел I и S наша теорема верна, значит, она верна и для многогранника М.

Объём произвольного тела определяется через объёмы соответствующих многогранников, поэтому теорема верна и для произвольного тела.

 

Теорема 2.2. (о задании подобия пространства) Если даны два тетраэдра ABCD и A´B´C´D´ такие, что , то существует ровно одно подобие пространства, при котором А→А´, В→В´, С→С´, D→D´.

 

Доказательство. То, что такое подобие существует, следует из теоремы 2.1 и теоремы о задании движения пространства (часть I, теорема 5.1). Пусть таких преобразований два: P и Р´. Тогда преобразование 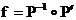– движение, имеющие неподвижные точки A, B, C, D, т.е. f – тождественное преобразование. Отсюда Р=Р´.

 

Задача 1.

Точки M, N, P расположены на сторонах АВ, ВС, АС треугольника АВС. Точки M´, N´, P´ симметричны точкам M, N, P относительно сторон АВ, ВС, АС. Доказать, что площади треугольников MNP и M´N´P´ равны.

Решение.

Для правильного треугольника утверждение очевидно.

Точно так же любую трапецию можно аффинным преобразованием перевести в равнобедренную, т.е. любое аффинное утверждение достаточно доказать для равнобедренной трапеции.

 

Задача 2.

В трапеции ABCD с основаниями AD и ВС через точку В проведена прямая, параллельная стороне CD и пересекающая диагональ АС в точке Р, а через точку С – прямая, параллельная стороне АВ и пересекающая диагональ BD в точке Q. Доказать, что прямая PQ параллельна основаниям трапеции.

Решение.

Для равнобедренной трапеции утверждение очевидно.

Сжатие к прямой.

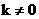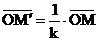Определение. Сжатием к прямой ℓ с коэффициентом k () называется преобразование, переводящее произвольную точку М в такую точку М´, что и , где .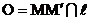

 

Теорема 2.1. Сжатие к прямой – аффинное преобразование.

 

Доказательство. Непосредственной проверкой убеждаемся, что прямая переходит в прямую. Можно даже заметить, что сжатие к прямой – частный случай параллельного проектирования (когда направление проектирования перпендикулярно линии пересечения плоскостей).

 

Теорема 2.2. Для любого аффинного преобразования существует квадратная решётка, которая при этом преобразовании переходит в прямоугольную решётку.

 

Доказательство. Возьмём произвольную квадратную решётку и рассмотрим один из её квадратиков ОАВС. Он при нашем преобразовании перейдёт в параллелограмм О´А´В´С´. Если О´А´В´С´ – прямоугольник, то наше доказательство закончено. В противном случае положим для определённости, что угол А´О´В´ – острый. Будем поворачивать квадрат ОАВС и всю нашу решётку вокруг точки О. Когда квадрат ОАВС повернётся на (так что точка А перешла в точку В), точка А´ перейдёт в точку В´, а В´ в вершину параллелограмма, смежного с О´А´В´С´. Т.е. угол А´О´В´ станет тупым. По принципу непрерывности, в какой-то момент он был прямым. В этот момент квадрат ОАВС переходил в прямоугольник, а наша решётка – в прямоугольную решётку, ч.т.д.

 

Теорема 2.3. Аффинное преобразование можно представить композицией сжатия к прямой и подобия.

 

Доказательство. Следует из теоремы 2.2.

 

Теорема 2.4. Аффинное преобразование, переводящее некоторую окружность в окружность, является подобием.

 

Доказательство. Опишем около нашей окружности квадрат и повернём его так, чтобы он переходил при нашем преобразовании в прямоугольник (теорема 2.2.). Наша окружность перейдёт в окружность, вписанную в этот прямоугольник, поэтому этот прямоугольник является квадратом. Теперь мы можем указать квадратную решётку, переходящую при нашем преобразовании в квадратную решётку. Очевидно, наше преобразование – подобие.

 

3. Аффинные преобразования пространства.

 

Определение. Аффинным преобразованием пространства называется преобразование пространства, переводящее каждую плоскость в плоскость.

 

Свойства.

1. При аффинном преобразовании прямые переходят в прямые.
2. Аффинное преобразование пространства индуцирует аффинное отображение каждой плоскости на её образ.
3. При аффинном преобразовании параллельные плоскости (прямые) переходят в параллельные плоскости (прямые).

 

Доказательства свойств.

1. Следует из того, что прямая есть пересечение двух плоскостей, и из определения аффинного преобразования.
2. Следует из определения аффинного преобразования и свойства 1.
3. Для плоскостей доказывается от противного, для прямых – через свойство 2 и свойство аффинного преобразования плоскости.

 

Теорема 3.1. (о задании аффинного преобразования пространства) Для любых данных тетраэдров АВСD и А´В´С´D´ существует единственное аффинное преобразование, переводящее А в А´, В в В´, С в С´, D в D´.

 

Доказательство. Доказывается аналогично теореме 1.1. (строятся решётки параллелепипедов).

 

Из доказательства теоремы 3.1 следует, что если у нас есть некоторая косоугольная система координат W, а W´ – её образ при аффинном преобразовании, то координаты произвольной точки пространства в системе координат W равны координатам её образа в системе координат W´.

Отсюда сразу вытекают ещё некоторые свойства аффинного преобразования.

1. Преобразование, обратное аффинному, является аффинным.
2. Аффинные преобразования сохраняют отношения длин параллельных отрезков.

 

Теперь пусть в пространстве задана система координат (О, , , 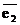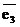) и аффинное преобразование f переводит О в О´ 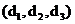, а базисные вектора в вектора , , 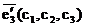соответственно. Найдём координаты x´, y´, z´ образа M´(x´,y´,z´) точки M(x,y,z) при преобразовании f.

Будем исходить из того, что точка М в системе координат (О, , , 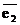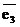) имеет такие же координаты, что и точка М´ в системе координат (О´, , , 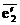). Отсюда

.

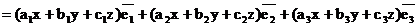Поэтому имеем равенства (*):

Стоит ещё заметить, что 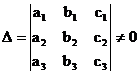, т.к. векторы , , 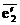линейно независимы.

Этот определитель называется определителем аффинного преобразования.

 

Теорема 3.2. Преобразование, заданное равенствами (*), при 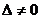является аффинным.

 

Доказательство. Достаточно проверить, что преобразование, обратное преобразованию(*), является аффинным (свойство 4). Возьмём произвольную плоскость Аx´+Вy´+Сz´+D=0, где А, В, С не равны одновременно нулю. Выполняя подстановки (*), получим уравнение её прообраза:

.

Остаётся лишь проверить, что в полученном уравнении коэффициенты при x, y, z одновременно не равны нулю. Это действительно так, т.к. иначе система

с неравным нулю определителем имела бы лишь нулевое решение: А=В=С=0, что неверно.

Теорема 3.3. Для объёмов V и V´ соответственных при аффинном преобразовании тел имеет место зависимость .

Доказательство. Пусть некомпланарные векторы , , 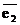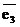образуют векторный базис пространства, и пусть в пространстве заданы векторы , и . Вычислив смешанное произведение этих векторов, получим:

.

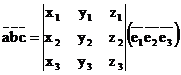Воспользуемся тем, что объём ориентированного параллелепипеда, построенного на векторах как на рёбрах, равен смешанному произведению этих векторов:

,

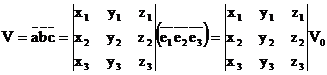где V₀ – объём параллелепипеда, построенного на базисных векторах.

Аффинное преобразование не изменяет координаты соответственных векторов в соответственных базисах. Поэтому для объёма V´ образа параллелепипеда объёма V имеем:

,

где – объём параллелепипеда, построенного на векторах , как на рёбрах.

Отсюда получаем: . Далее 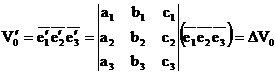, поэтому для неориентированных объёмов имеем . На все тела это равенство можно распространить аналогично доказательству свойства 4 подобий (часть II, §2).

 

Задача.

Вершина параллелепипеда соединена с центрами трёх не содержащих её граней. Найдите отношение объёма полученного тетраэдра к объёму данного параллелепипеда.

Решение.

Посчитаем данное отношение для куба и, переведя аффинным преобразованием куб в параллелепипед, воспользуемся тем, что аффинное преобразование сохраняет отношение объёмов. Для куба отношение легко считается. Оно равно 1:12.

Ответ: 1:12.

 

Родство пространства.

Определение. Аффинное преобразование пространства, имеющее плоскость неподвижных точек, называется родственным преобразованием ρ (родством), а плоскость его неподвижных точек называется плоскостью родства. Соответственные при родстве элементы называются родственными.

 

Определение. Направление прямых, соединяющих родственные точки, называется направлением родства.

 

Свойства родства.

1. Родственные прямые (плоскости) пересекаются на плоскости родства или ей параллельны.
2. (Корректность определения направления родства) Прямые, каждая из которых соединяет две родственные точки, параллельны.
3. Если направление родства непараллельно плоскости этого родства, то каждый отрезок, соединяющий две родственные точки, делится плоскостью родства в одном и том же отношении.
4. Всякая плоскость, параллельная направлению родства, неподвижна при этом родстве. В ней индуцируется родство плоскости (аффинное преобразование, имеющее прямую неподвижных точек, называющуюся осью родства), осью которого является прямая её пересечения с плоскостью данного родства пространства.

 

Доказательства свойств.

1. Доказательство аналогично доказательству свойства зеркальной симметрии (часть I, §3.5).

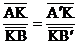2. Пусть А, В – две различные точки; А´, В´ – их образы при родстве, α – плоскость родства. Пусть . Тогда (свойство аффинного преобразования), т.е. АА´||ВВ´, ч.т.д.

3 и 4. Следуют из доказательства свойства 2.

 

Определение. Поверхность, представляемая уравнением 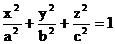, называется эллипсоидом. Частным случаем эллипсоида является сфера.

 

Имеет место следующий факт, который мы доказывать не будем, однако, при доказательстве следующих теорем он нам понадобится:

Теорема 4.1. Аффинное преобразование переводит эллипсоид в эллипсоид.

Теорема 4.2. Произвольное аффинное преобразование пространства представимо композицией подобия и родства.

 

Доказательство. Пусть аффинное преобразование f отображает сферу σ на эллипсоид σ´. Из теоремы 3.1 следует, что f может быть задано этими фигурами. Рассмотрим плоскость α´, содержащую центр эллипсоида и пересекающую его по некоторой окружности ω´ (существование такой плоскости легко доказать из соображений непрерывности). Пусть α – прообраз α´, 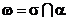– прообраз ω´, β – сфера, имеющая окружность ω´ своей диаметральной окружностью. Существует родство ρ, отображающее β на σ´, и существует подобие P, отображающее σ на β. Тогда – искомое представление.

 

Из доказательства предыдущей теоремы сразу следует теорема 4.3:

Теорема 4.3. Аффинное преобразование, сохраняющее сферу, является подобием.

 

 

Часть IV. Проективные преобразования.

1. Проективные преобразования плоскости.

Определение. Проективная плоскость – обычная (евклидова)плоскость, дополненная бесконечно удаленными точками и бесконечно удаленной прямой, называемыми также несобственными элементами. При этом каждая прямая дополняется одной несобственной точкой, вся плоскость – одной несобственной прямой; параллельные прямые дополняются общей несобственной точкой, непараллельные – разными; несобственные точки, дополняющие всевозможные прямые плоскости, принадлежат несобственной прямой.

 

Определение. Преобразование проективной плоскости, переводящее любую прямую в прямую, называется проективным.

 

Следствие. Проективное преобразование, сохраняющее бесконечно удалённую прямую является аффинным; любое аффинное преобразование является проективным, сохраняющим бесконечно удалённую прямую.

 

Определение. Центральным проектированием плоскости α на плоскость β с центром в точке О, не лежащей на этих плоскостях, называется отображение, которое любой точке А плоскости α ставит в соответствие точку А´ пересечения прямой ОА с плоскостью β.

При этом, если плоскости α и β не параллельны, то в плоскости α найдётся прямая ℓ такая, что плоскость, проходящая через точку О и прямую ℓ, параллельна плоскости β. Будем считать, что ℓ при нашем проектировании переходит в бесконечно удалённую прямую плоскости β (при этом каждая точка B прямой ℓ переходит в ту точку бесконечно удалённой прямой, что дополняет прямые параллельные ОВ). В плоскости β найдётся прямая ℓ´ такая, что плоскость, проходящая через точку О и прямую ℓ´, параллельна плоскости α. Будем считать ℓ´ образом бесконечно удалённой прямой плоскости α. Прямые ℓ и ℓ´ будем называть выделенными.

Мы можем говорить, что задано просто преобразование проективной плоскости (если совместить плоскости α и β).

 

Из определения сразу вытекают свойства центральной проекции:

1. Центральное проектирование – проективное преобразование.
2. Обратное к центральному проектированию преобразование – центральное проектирование с тем же центром.
3. Прямые, параллельные выделенным, переходят в параллельные.

 

Определение. Пусть точки А, В, С, D лежат на одной прямой. Двойным отношением (АВ; СD) этих точек называется величина 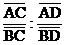. Если одна из точек является бесконечно удалённой, то длины отрезков, концом которых является эта точка, можно сократить.

 

Теорема 1.1. Центральная проекция сохраняет двойные отношения.

 

Доказательство. Пусть О – центр проектирования, А, В, С, D – четыре точки, лежащие на одной прямой, A´, B´, C´, D´ – их образы.

Тогда .

Аналогично .

Поделив одно равенство на другое, получим .

Аналогично, вместо точки С рассматривая точку D, получим .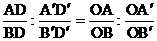

Отсюда , т.е. .

Чтобы доказательство было полным, осталось заметить, что все отрезки, площади и углы можно считать ориентированными.

 

Теорема 1.2. Пусть даны четыре точки A, B, C, D плоскости π, не лежащие на одной прямой, и четыре точки M, N, P, Q плоскости π´, не лежащие на одной прямой. Тогда существует композиция центральной (параллельной) проекции и подобия, переводящая A в M, В в N, С в Р, D в Q.

 

Доказательство.

Будем для удобства говорить, что ABCD и MNPQ – четырёхугольники, хотя на самом деле это не обязательно (например, могут пересекаться отрезки АВ и CD). Из доказательства будет видно, что мы нигде не используем, что точки A, В, С, D и M, N, P, Q в указанном порядке образуют четырёхугольники.

I. Если наши четырёхугольники – трапеции (АD||BC и MQ||NP), то доказательство совсем простое. Рассмотрим четырёхугольник A´B´C´D´, подобный четырёхугольнику MNPQ, такой, что AD=A´D´. Расположим плоскости π и π´ так, чтобы совпали точки А с А´ и D с D´. Теперь, если 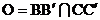, то нужный нам результат даст центральная проекция с центром О (см. рис.), а если ВВ´||CC´, то нужный нам результат даст параллельная проекция с направлением ВВ´.

II. Теперь докажем утверждение, если четырёхугольники произвольные. Пусть , 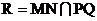. Отметим точки Х₁, Х₂, Z₁, Z₂ на прямых АВ, CD, MN, PQ соответственно так, что

; ; ; .

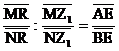Проведём теперь через точки A, B, C, D прямые АK, BL, CF, DG, параллельные X₁X₂ (K, L лежат на DC; G, F – на АВ), а через точки N, M – прямые NT, MS, параллельные Y₁Y₂ (T, S лежат на PQ). Переведём центральной (параллельной) проекцией f трапецию АВLK в трапецию А´В´L´K´ плоскости π´, подобную трапеции MNTS (это возможно по части I нашего доказательства). При этом из выбора точек Х₁, Х₂ следует, что прямая Х₁Х₂ – выделенная прямая плоскости π´. Отметим на прямой L´K´ точки С´, D´ такие, что трапеция ABCD подобна трапеции A´B´C´D´. Проведём прямые C´F´, D´G´, параллельные прямой B´L´ (F´, G´ лежат на А´В´), и отметим на прямой А´В´ точку Y₁´ такую, что 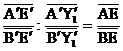, . На прямой C´D´ отметим точку Y₂´ такую, что Y₁´Y₂´||A´K´ (см. рис.). Из выбора точек Y₁´ и Y₂´ следует, что прямая Y₁´Y₂´ – выделенная прямая плоскости π´. При преобразовании f точка Е переходит в точку Е´ пересечения прямых A´B´ и L´K´. Точка С переходит в некоторую точку С₀´ прямой С´D´.

Докажем, что С₀ совпадает с С´. Из того, что Х₂ при преобразовании f переходит в бесконечно удалённую точку прямой C´D´, а Y₂´ - образ бесконечно удалённой точки прямой CD и центральная проекция сохраняет двойные отношения, следует, что , откуда 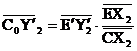. Теперь рассмотрим преобразование g, композицию центральной проекции и подобия, переводящее трапецию CDGF в трапецию C´D´G´F´. Для преобразования g аналогично можно показать, что . Отсюда будет следовать, что точки С₀ и С´ совпадают. Аналогично можно показать, что D₀ – образ точки D при преобразовании f – совпадает с D´. Итак, преобразование f переводит четырёхугольник ABCD в четырёхугольник A´B´C´D´, подобный четырёхугольнику MNPQ, что и требовалось.

 

Теорема 1.3. Пусть даны четвёрки точек, из которых никакие три не лежат на одной прямой: A, B, C, D и A´, B´, C´, D´. Тогда существует единственное проективное преобразование, переводящее А в А´, В в В´, С в С´, D в D´.

 

Существование такого преобразования следует из теоремы 1.1.

Единственность можно доказывать так же, как и единственность аффинного преобразования (теорема 1.1, часть III): рассматривать квадратную решётку, строить её образ, а затем измельчать. Обойти те трудности, с которыми мы столкнулись п