УДК 53
ББК 22.3
© ГОУ ВПО «Омский государственный
технический университет», 2009
ВВЕДЕНИЕ
Физика – в своей основе экспериментальная наука. Выявленные ею объективные законы природы получены чаще всего в результате экспериментальных исследований.
Работа в лабораториях физического практикума является частью процесса изучения как физических законов, так и методов, применяемых в физике.
Целями физического практикума являются:
а) иллюстрация теоретических положений физики;
б) знакомство с измерительными приборами;
в) приобретение опыта проведения экспериментов;
г) выработка навыков, необходимых для учёта различного рода погрешностей и оценки точности полученного результата;
д) развитие умения делать правильные выводы при анализе экспериментальных данных.
ЧАСТЬ 1
МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Измерения. Погрешности измерений
Каждая из лабораторных работ физического практикума ставит своей целью изучение определенного физического явления и связана с измерением той или иной величины, характеризующей данное явление.
Измерением называется нахождение значения физической величины опытным путем с помощью специальных технических средств.
По способу получения различают прямые и косвенные измерения.
Прямым называется такое измерение, в котором значение физической величины получают в результате опыта с помощью прибора, проградуированного в соответствующих единицах. Примеры: измерение массы с помощью весов, промежутков времени – секундомером, длины – линейкой или штангенциркулем, тока – амперметром и т.д.
Прямые измерения могут быть однократными (физическая величина измеряется один раз) и многократными (физическая величина измеряется несколько раз в одних и тех же условиях одним и тем же измерительным прибором).
Косвенным называют такое измерение, в котором значение физической величины получают вычислением на основании известной зависимости между этой величиной и величинами, полученными при прямых измерениях. Примеры: определение плотности материала по измеренным массе и объёму; сопротивления проводника – по измеренным напряжению и току и т.д.
Измерить в реальном эксперименте какую-либо физическую величину абсолютно точно, т.е. получить ее истинное значение, невозможно
[1, 2]. На результат измерения могут оказывать влияние различные факторы. Это влияние проявляется как погрешность. Другими словами, измеренное значение величины всегда отличается от истинного.
Aбсолютной погрешностью  измерения называется разность между результатом измерения и истинным значением измеряемой величины. Абсолютная погрешность выражается в единицах измеряемой величины.
измерения называется разность между результатом измерения и истинным значением измеряемой величины. Абсолютная погрешность выражается в единицах измеряемой величины.
Наряду с абсолютной погрешностью используется относительная погрешность  , равная отношению абсолютной погрешности к результату измерения. Относительная погрешность может быть выражена в процентах, она характеризует точность измерений (чем меньше величина относительной погрешности, тем выше точность измерений).
, равная отношению абсолютной погрешности к результату измерения. Относительная погрешность может быть выражена в процентах, она характеризует точность измерений (чем меньше величина относительной погрешности, тем выше точность измерений).
Пример обработки результатов
Прямых измерений
Пример. В результате пяти измерений диаметра некоторого цилиндра, выполненных штангенциркулем, точность которого 0,1 мм, получены следующие значения: 



 . Необходимо определить доверительный интервал, в пределах которого с заданной доверительной вероятностью (надежностью) лежит истинное значение диаметра цилиндра.
. Необходимо определить доверительный интервал, в пределах которого с заданной доверительной вероятностью (надежностью) лежит истинное значение диаметра цилиндра.
1) По формуле (7) вычислим среднее арифметическое значение 
 .
.
(Расчет среднего значения производится с числом значащих цифр, превышающим на единицу число значащих цифр в результатах измерений).
2) По формуле (8) вычислим погрешности отдельных измерений:

3)По формуле (9) вычислим среднеквадратичную погрешность 
 .
.
4) Задаем значение доверительной вероятности 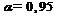 . По таблице определяем значение коэффициента Стьюдента
. По таблице определяем значение коэффициента Стьюдента 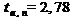 (при
(при  и
и 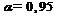 ).
).
5) По формуле (10) вычислим случайную погрешность  :
:
 .
.
6) По формуле (11) оценим погрешность  , даваемую штангенциркулем:
, даваемую штангенциркулем:
 .
.
7) По формуле (12) вычислим абсолютную погрешность результата измерений 
 .
.
8) По формуле (13) вычислим относительную погрешность 
 .
.
( При расчете погрешностей (  ,
,  ,
,  и
и  ) рекомендуется оставлять три значащих цифры, а округление проводить только при записи окончательного результата).
) рекомендуется оставлять три значащих цифры, а округление проводить только при записи окончательного результата).
9) Запишем окончательный результат:
 ,
,
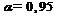 ;
; 
(Значение  округлили в большую сторону до двух значащих цифр, поскольку первая значащая цифра 1).
округлили в большую сторону до двух значащих цифр, поскольку первая значащая цифра 1).
Замечание. Все вычисления выполнены в соответствии с правилами, изложенными в 1.10.
Пример обработки результатов
Косвенных измерений
Пример. Определить массу шара по известному значению плотности материала  и измеренному многократно диаметру
и измеренному многократно диаметру  :
:  (погрешность диаметра определялась с надежностью
(погрешность диаметра определялась с надежностью 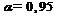 ). Оценить погрешности определения массы.
). Оценить погрешности определения массы.
1) Находим среднее значение массы по формуле:
 .
.
(В соответствии с правилами приближенных вычислений в этом, еще неокончательном результате, сохранена одна запасная цифра.)
2)Выведем формулу для относительной погрешности  , воспользовавшись (19), поскольку выражение для
, воспользовавшись (19), поскольку выражение для 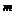 легко логарифмируется.
легко логарифмируется.

Логарифмируем функцию  и находим частные производные по соответствующим переменным:
и находим частные производные по соответствующим переменным:
 .
.
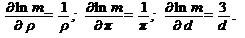
Подставим полученные выражения производных в формулу для  :
:
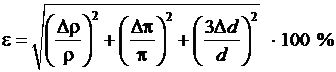
3) Вычислим относительную погрешность:


(Погрешность табличной величины  принимаем равной 0,5 единицы наименьшего разряда числа
принимаем равной 0,5 единицы наименьшего разряда числа  , т.е.
, т.е. 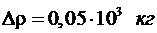 . Погрешность числа
. Погрешность числа  также принимаем равной 0,5 единицы наименьшего разряда числа 3.14, т. е.
также принимаем равной 0,5 единицы наименьшего разряда числа 3.14, т. е.  ).
).
4) Вычислим абсолютную погрешность  , воспользовавшись формулой (20):
, воспользовавшись формулой (20):
 .
.
5) Запишем окончательный результат, соблюдая правила округления при его записи:
 .
.
Замечание. Все вычисления выполнены в соответствии с правилами, изложенными в 1.10.
ЧАСТЬ 2
ОФОРМЛЕНИЕ РЕЗУЛЬТАТОВ РАБОТЫ
Подготовка к выполнению лабораторной работы
В начале семестра студентам сообщается учебный план на семестр, в нём указывается количество лабораторных работ, которые необходимо выполнить в течение семестра.
Каждая лабораторная работа рассчитана на одно занятие.
Выполнение всех работ физического практикума включает самостоятельную подготовку, которая должна быть закончена к началу занятия.
Можно выделить несколько этапов самостоятельной подготовки:
1) знакомство с описанием лабораторной работы (по методическим указаниям);
2) изучение теоретического материала по теме, рассматриваемой в лабораторной работе;
3) самопроверка готовности к выполнению лабораторной работы;
4) подготовка конспекта отчета к лабораторной работе.
Проверить степень своей готовности к выполнению конкретной работы можно с помощью обобщенных контрольных вопросов, общих для всех работ физического практикума.
Вопросы для самопроверки готовности к выполнению
Лабораторной работы
1) Какова цель работы?
2) Какое физическое явление или закон изучается в данной работе?
3) Какими физическими зависимостями связаны величины, описывающие данное явление?
4) Какая теоретическая зависимость может быть проверена в данном опыте?
5) Какие физические явления положены в основу экспериментального метода определения искомых величин?
6) Какие допущения сделаны при описании теории метода?
7) Какое уравнение (или система уравнений) позволяет найти искомую величину или нужную зависимость на основании опытных данных?
8) Какие конкретные задачи придется решать в ходе эксперимента для достижения цели?
9) Что представляет объект исследования в данной работе?
10) Каково назначение отдельных узлов экспериментальной установки?
11) Какие измерительные приборы будут использоваться при проведении опытов?
12) Какие физические величины будут измеряться непосредственно, а какие будут получены в результате вычислений?
13) Какие постоянные (табличные данные, параметры образца или установки) нужны для определения искомой величины по данным опыта?
14) Какие графики должны быть построены по полученным данным?
15) Как придется оценивать погрешность конечного результата?
16) Как можно проверить надежность полученных экспериментальных данных?
17) Можно ли сопоставить результаты эксперимента с литературными данными?
Рекомендации по оформлению отчета
По лабораторной работе
Лабораторные работы оформляются в специальном журнале лабораторных работ, в отдельной тетради или на отдельных бланках (листах).
Отчет по лабораторной работе составляется по следующей схеме:
1) Название и номер лабораторной работы.
2) Цель работы.
3) Используемые приборы и принадлежности.
4) Краткая теория. (Здесь кратко излагаются теоретические положения, лежащие в основе эксперимента. Указывается, какие законы и зависимости проверяются, какие соотношения используются при выводе рабочих формул. Приводятся расчетные формулы с пояснениями. Рекомендуется сделать схематический рисунок, поясняющий идею данного эксперимента, а также начертить электрическую или оптическую схемы, если они применяются в лабораторной работе).
5) Таблицы.
6) Расчет искомых величин и их погрешностей.
7) Графики.
8) Выводы.
В начале занятия студент предъявляет преподавателю подготовленный конспект отчета лабораторной работы. Допуск к выполнению лабораторной работы студент получает после собеседования с преподавателем.
Для получения допуска к выполнению лабораторной работы
студент должен знать:
1) название работы;
2) цель работы;
3) используемые приборы и оборудование;
4) формулировки физических законов и соотношений, используемых при выводе рабочих формул; определения физических величин, прямо или косвенно измеряемых в данной работе;
5) порядок выполнения лабораторной работы; какие величины измеряются прямыми методами, а какие определяются в данной работе в результате косвенных измерений;
6) вид представления результата:
а) измеренная величина с погрешностями;
б) соотношения;
в) графическая зависимость.
Окончание эксперимента отмечается в рабочем журнале студента и журнале преподавателя.
Оформленный отчет о работе (с математической обработкой результатов измерений и выводами) сдается на следующем занятии или на специально отведенном (итоговом) занятии.
В выводах по работе необходимо отразить:
1) что и как исследовалось (измерялось);
2) результаты, полученные в лабораторной работе;
3) анализ полученных результатов:
а) как согласуются результаты, полученные в лабораторной работе, с известными теоретическими выводами и соотношениями;
б) при наличии расхождений с тем, что предсказывает теория, объяснить возможные причины.
Метод наименьших квадратов
В задачи экспериментальной физики входит не только измерение конкретных величин, но и исследование зависимостей между физическими характеристиками.
Пусть в результате эксперимента получен ряд значений величины 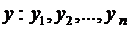 , соответствующих значениям аргумента
, соответствующих значениям аргумента 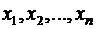 , и необходимо построить график зависимости
, и необходимо построить график зависимости 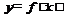 .
.
Характер теоретической зависимости 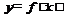 обычно бывает известен из физического смысла задачи (например,
обычно бывает известен из физического смысла задачи (например,  зависит от
зависит от 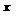 по линейному или квадратичному закону). Однако экспериментальные точки вследствие неизбежных погрешностей, возникающих при измерениях, имеют разброс относительно ожидаемой графической зависимости.
по линейному или квадратичному закону). Однако экспериментальные точки вследствие неизбежных погрешностей, возникающих при измерениях, имеют разброс относительно ожидаемой графической зависимости.
Задача экспериментатора − провести по экспериментальным точкам линию, которая давала бы наилучшее согласие между экспериментальными результатами и теоретической зависимостью 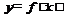 .
.
Для решения подобных задач применяется метод наименьших квадратов (МНК).
Ограничимся случаем, когда ожидаемую зависимость между 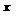 и
и  можно полагать линейной. Тогда функция
можно полагать линейной. Тогда функция 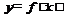 записывается в следующем виде:
записывается в следующем виде:
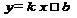 . (21)
. (21)
В основе МНК лежит положение, согласно которому наилучшим приближением к теоретической будет такая прямая линия, для которой сумма квадратов разностей экспериментальных значений  и соответствующих вычисленных значений
и соответствующих вычисленных значений 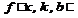 является минимальной.
является минимальной.
То есть наиболее вероятные значения параметров  и
и 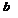 выбирают так, чтобы сумма была минимальной:
выбирают так, чтобы сумма была минимальной:
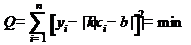 .
.
Условие минимума  выполняется, если равны нулю частные производные
выполняется, если равны нулю частные производные  и
и  :
:
 ,
,
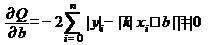 .
.
Записанные соотношения являются системой линейных алгебраических уравнений:
 , (22)
, (22)
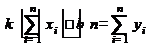 . (23)
. (23)
Решение системы уравнений (22) и (23) приводит к следующим значениям искомых параметров  и
и 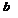 :
:
 , (24)
, (24)
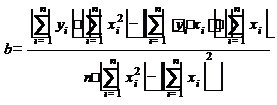 . (25)
. (25)
Примечание. Значения параметров  и
и 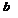 не изменится, если ввести в (24) и (25) другие переменные:
не изменится, если ввести в (24) и (25) другие переменные:
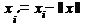 ;
; 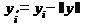 ,
,
где 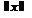 и
и 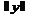 определяются соответственно как
определяются соответственно как
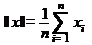 ,
,  ,
,
однако расчетные формулы  и
и 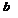 при этом упрощаются:
при этом упрощаются:
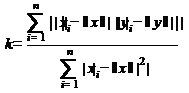 , (26)
, (26)
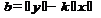 . (27)
. (27)
Коэффициенты, вычисленные по формулам (24) и (25) или (26) и (27), полагаются наилучшими приближенными значениями (оценками) параметров  и
и 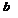 линейной функции (21). Их значения можно использовать для вычисления
линейной функции (21). Их значения можно использовать для вычисления 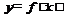 при произвольных значениях аргумента
при произвольных значениях аргумента 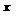 .
.
В тех случаях, когда до опыта известно, что зависимость 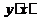 проходит через начало координат, т.е. ожидаемую зависимость можно представить в виде
проходит через начало координат, т.е. ожидаемую зависимость можно представить в виде
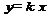 , (28)
, (28)
значение параметра  , согласно МНК, находят из условия минимума суммы:
, согласно МНК, находят из условия минимума суммы:
 . (29)
. (29)
Дифференцируя (29) по параметру  и приравнивая
и приравнивая  нулю, получаем:
нулю, получаем:
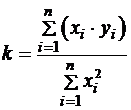 . (30)
. (30)
Рассчитанное по формуле (30) значение параметра  является наилучшим в функциональной зависимости
является наилучшим в функциональной зависимости 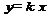 .
.
Метод наименьших квадратов дает не истинные параметры  и
и 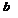 в линейной зависимости
в линейной зависимости 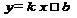 , а их наиболее вероятные приближённые значения. Следовательно, при построении искомой прямой линии, аппроксимирующей экспериментальную зависимость, кроме значений параметров
, а их наиболее вероятные приближённые значения. Следовательно, при построении искомой прямой линии, аппроксимирующей экспериментальную зависимость, кроме значений параметров  и
и 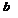 , необходимо в общем случае знать и доверительные интервалы, в которых они лежат. Для этого требуется оценить среднеквадратичные погрешности, с которыми
, необходимо в общем случае знать и доверительные интервалы, в которых они лежат. Для этого требуется оценить среднеквадратичные погрешности, с которыми  и
и 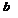 определены.
определены.
Математическая статистика даёт следующие выражения для среднеквадратичных погрешностей параметров  и
и 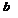 :
:
 , (31)
, (31)
 . (32)
. (32)
В частном случае, когда прямая проходит через точку  ,
, 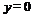 , вычисляют среднеквадратичную погрешность определения только параметра
, вычисляют среднеквадратичную погрешность определения только параметра  :
:
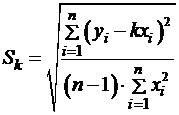 . (33)
. (33)
Полуширину доверительного интервала, с которой определено значение параметра  , вычисляют по стандартной методике:
, вычисляют по стандартной методике:
 , (34)
, (34)
здесь 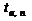 – коэффициент Стьюдента для надежности
– коэффициент Стьюдента для надежности 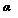 и числа пар точек
и числа пар точек 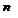 .
.
Пример. В эксперименте получено пять измерений величин 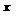 и
и  , результаты которых приведены в таблице. Известно, что уравнение измерения имеет вид
, результаты которых приведены в таблице. Известно, что уравнение измерения имеет вид 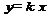 . Используя метод наименьших квадратов, рассчитать наилучшее значение коэффициента
. Используя метод наименьших квадратов, рассчитать наилучшее значение коэффициента  и погрешность
и погрешность 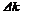 , с которой этот коэффициент определён. Построить наилучшую прямую.
, с которой этот коэффициент определён. Построить наилучшую прямую.
Для наглядности сведём исходные данные и результаты расчетов в таблицу.
|
| 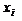
| 
| 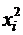
| 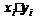
| 
| 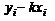
| 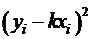
| 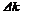
|
|
| 0,4
0,8
1,2
1,6
2,0
| 0,50
1,40
1,66
2,80
3,20
| 0,16
0,64
1,44
2,56
4,00
| 0,20
1,12
1,99
4,48
6,40
|
1,61
| -0,144
0,112
-0,272
0,224
-0,020
| 0,0207
0,0125
0,0740
0,0502
0,0004
|
0,19
|
1) По формуле (30) найдем величину параметра  :
:
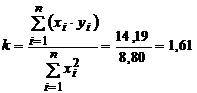
2) По формуле (33) оценим среднеквадратичную погрешность определения параметра  :
:
 .
.
3) Задаем значение доверительной вероятности 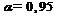 . По таблице определяем значение коэффициента Стьюдента
. По таблице определяем значение коэффициента Стьюдента 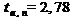 (при
(при  и
и 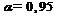 ).
).
4) По формуле (34) вычислим абсолютную погрешность определения параметра  :
:
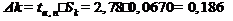 .
.
5) Окончательный результат:
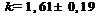 при доверительной вероятности
при доверительной вероятности 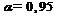 .
.
6) Запишем уравнение наиболее правдоподобной прямой:
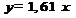 .
.
 7) Поскольку зависимость
7) Поскольку зависимость 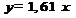 линейная, то для построения графика достаточно найти только одну точку и провести прямую через начало координат и найденную точку. Эта прямая (см. рис.) и будет "наилучшей" прямой, описывающей заданную функциональную зависимость.
линейная, то для построения графика достаточно найти только одну точку и провести прямую через начало координат и найденную точку. Эта прямая (см. рис.) и будет "наилучшей" прямой, описывающей заданную функциональную зависимость.
Примечание. Если экспериментальная зависимость заменяется аналитическим уравнением прямой линии, то при определении абсолютной погрешности величины  , соответствующей значению аргумента
, соответствующей значению аргумента 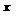 , применяется метод переноса ошибок (см. 1.7). В частности, если прямая проходит через начало координат, абсолютная погрешность
, применяется метод переноса ошибок (см. 1.7). В частности, если прямая проходит через начало координат, абсолютная погрешность 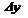 равна:
равна:
 ,
,
где 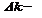 абсолютная погрешность определения параметра
абсолютная погрешность определения параметра  .
.
ЧАСТЬ 3
ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Распределение Гаусса
Одним из наиболее важных непрерывных распределений, встречающихся в статистике, является нормальное распределение, или распределение Гаусса. Плотность вероятности  этого распределения имеет вид:
этого распределения имеет вид:
 . (36)
. (36)
Параметр 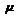 в (36) называется математическим ожиданием, а
в (36) называется математическим ожиданием, а  − дисперсией случайной величины (определения
− дисперсией случайной величины (определения 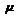 и
и  будут даны ниже).
будут даны ниже).
График функции распределения Гаусса (36) изображен на рисунке.

По оси абсцисс откладывается значения 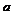 случайной величины
случайной величины  , по оси ординат − плотность вероятности. Функция плотности
, по оси ординат − плотность вероятности. Функция плотности 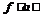 представляет колоколообразную симметричную кривую, имеющую максимум при
представляет колоколообразную симметричную кривую, имеющую максимум при 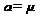 , а точки
, а точки 
 являются точками перегиба. График нормального закона распределения зависит от параметра
являются точками перегиба. График нормального закона распределения зависит от параметра  . Чем больше
. Чем больше  , тем более пологий вид имеет кривая распределения.
, тем более пологий вид имеет кривая распределения.
Функция (36) является нормированной на единицу, это значит, что площадь, заключенная между кривой плотности вероятности 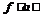 и осью абсцисс, равна единице. Другими словами, вероятность того, что величина
и осью абсцисс, равна единице. Другими словами, вероятность того, что величина  имеет произвольное значение в интервале
имеет произвольное значение в интервале  , равна единице. Расчеты показывают, что вероятность того, что значение случайной величины
, равна единице. Расчеты показывают, что вероятность того, что значение случайной величины  попадет в интервал
попадет в интервал  равна
равна 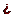 68 %. Это значит, что почти в 70 % случаев значение величины
68 %. Это значит, что почти в 70 % случаев значение величины  находится в довольно узком доверительном интервале.
находится в довольно узком доверительном интервале.
1) Математическое ожидание 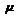 случайной величины
случайной величины  есть среднее арифметическое значение
есть среднее арифметическое значение 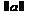 , и для непрерывного распределения оно равно значению интеграла:
, и для непрерывного распределения оно равно значению интеграла:
 .
.
Параметр 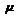 является наиболее вероятным значением случайной величины
является наиболее вероятным значением случайной величины  .
.
2) Дисперсией  случайной величины
случайной величины  называется математическое ожидание функции
называется математическое ожидание функции 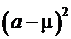 , и для непрерывного распределения оно равно значению интеграла:
, и для непрерывного распределения оно равно значению интеграла:
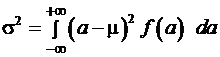 .
.
Дисперсия характеризует разброс значений случайной величины  относительно
относительно 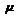 . Каждый метод измерения, а также измерительный прибор характеризуется своим значением
. Каждый метод измерения, а также измерительный прибор характеризуется своим значением 
Если значение дисперсии  не известно, то наилучшей оценкой ее является квадрат среднеквадратичной погрешности
не известно, то наилучшей оценкой ее является квадрат среднеквадратичной погрешности 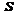 :
:
 .
.
(Величина  при
при 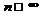 вообще совпадает с
вообще совпадает с  ).
).
Квадратный корень из дисперсии  называется стандартным отклонением значения
называется стандартным отклонением значения 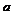 от
от 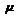 .
.
Разность 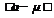 в (36) – это величина погрешности, следовательно, значение функции (35), записанное для
в (36) – это величина погрешности, следовательно, значение функции (35), записанное для 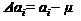 , является плотностью вероятности появления данной погрешности. Соответствующий закон распределения запишется в виде:
, является плотностью вероятности появления данной погрешности. Соответствующий закон распределения запишется в виде:
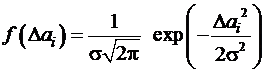 . (37)
. (37)
Максимум кривой (37) приходится на  . Это значит, что, когда плотность вероятности появления той или иной погрешности подчиняется нормальному закону, малые погрешности являются более вероятными, чем большие.
. Это значит, что, когда плотность вероятности появления той или иной погрешности подчиняется нормальному закону, малые погрешности являются более вероятными, чем большие.
Распределение Гаусса является основным в теории погрешностей. Обоснованием данного утверждения является центральная предельная теорема статистики.
Теорема. Пусть случайная величина  имеет среднее значение
имеет среднее значение 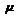 и дисперсию
и дисперсию  . Если
. Если  конечно, то при стремлении числа измерений случайной величины
конечно, то при стремлении числа измерений случайной величины  к бесконечности распределение среднего арифметического
к бесконечности распределение среднего арифметического 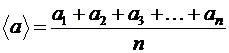 будет стремиться к нормальному распределению с тем же математическим ожиданием
будет стремиться к нормальному распределению с тем же математическим ожиданием 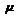 и дисперсией
и дисперсией 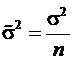 .
.
Благодаря этой теореме, доверительную вероятность 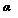 того, что это среднее
того, что это среднее 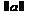 лежит внутри выбранного доверительного интервала
лежит внутри выбранного доверительного интервала 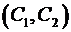 , можно найти с помощью соотношения:
, можно найти с помощью соотношения:
 . (38)
. (38)
Записанная теорема по сути утверждает, что во многих случаях, имеющих место в физических экспериментах, неважно, какому распределению подчиняются случайные погрешности измерения физической величины  , её среднее значение
, её среднее значение 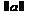 распределено по гауссовому закону (36) около наиболее вероятного значения
распределено по гауссовому закону (36) около наиболее вероятного значения 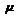 , которое можно считать истинным значением измеряемой величины. Именно поэтому практически во всех случаях экспериментальные погрешности можно вычислять, пользуясь одними и теми же методами, часть которых изложена в данном пособии.
, которое можно считать истинным значением измеряемой величины. Именно поэтому практически во всех случаях экспериментальные погрешности можно вычислять, пользуясь одними и теми же методами, часть которых изложена в данном пособии.
ПРИЛОЖЕНИЕ
Значения коэффициентов Стьюдента
Таблица 1
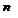
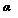
|
|
|
|
|
|
|
|
|
| 
|
| 0,8
| 3,08
| 1,89
| 1,64
| 1,53
| 1,48
| 1,44
| 1,42
| 1,40
| 1,38
| 1,3
|
| 0,9
| 6,31
| 2,92
| 2,35
| 2,13
| 2,02
| 1,94
| 1,90
| 1,86
| 1,83
| 1,65
|
| 0,95
| 12,7
| 4,30
| 3,18
| 2,78
| 2,57
| 2,45
| 2,36
| 2,31
| 2,26
| 1,96
|
 число измерений;
число измерений;  доверительная вероятность, или надежность.
доверительная вероятность, или надежность.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Зайдель А. Н. Элементарные оценки ошибок измерений / А. Н. Зайдель. – Л.: Наука, 1967. – 89 с.
2. Тойберг П. Оценка точности результатов измерений / П. Тойберг. – М.: Энергоиздат, 1988. –88 с.
3. Худсон Д. Статистика для физиков / Д. Худсон. – М.: Мир, 1970. – 296 с.
4. Деденко Л. Г. Математическая обработка и оформление результатов эксперимента / Л. Г. Деденко, В. В. Керженцев. – М.: Изд-во МГУ, 1977. – 121 с.
ОГЛАВЛЕНИЕ
Введение............................................................................................................. 3
Часть 1. Математическая обработка результатов измерений................ 4
1.1. Измерения. Погрешности измерений.............................................................. 4
1.2. Учет случайных погрешностей при прямых измерениях.............................. 6
1.3. Учет систематических (приборных) погрешностей
при прямых измерениях..................................................................................... 7
1.4. Совместный учёт случайных и систематических
(приборных) погрешностей............................................................................... 8
1.5. Последовательность действий при обработке
результатов многократных прямых измерений............................. 9
1.6. Пример обработки результатов прямых измерений.................... 10
1.7 Учёт погрешностей при косвенных измерениях.......................... 12
1.8. Последовательность действий при обработке
результатов косвенных измерений............................................... 15
1.9. Пример обработки результатов косвенных измерений.............. 17
1.10. Правила работы с приближёнными числами. Правила
округления при записи окончательного результата
измерений.......................................................................................................... 18
Часть 2. Правила работы в лаборатории, оформление
результатов работы......................................................................................... 20
2.1. Подготовка к выполнению лабораторной работы....................... 20
2.2. Графическое представление результатов измерений................. 23
2.3. Метод наименьших квадратов....................................................... 24
Часть 3. Элементы теории вероятностей и математической
статистики........................................................................................................ 31
3.1. Вероятность. Плотность вероятности........................................... 31
3.2. Распределение Гаусса..................................................................... 32
Приложение..................................................................................................... 36
Библиографический список......................................................................... 37
Редактор Л. И. Чигвинцева
Компьютерная верстка – Е. В. Беспалова
ИД № 06039 от 12.10.2001 г.
Сводный темплан 2009 г.
Подписано в печать 22.06.09. Формат 60×84 1/16. Бумага офсетная.
Отпечатано на дупликаторе. Усл. печ. л. 2,5. Уч.-изд. л. 2,5.
Тираж 250 экз. Заказ 455.
_________________________________________________________
Издательство ОмГТУ. 644050, г. Омск, пр. Мира, 11; т. 23-02-12
Типография ОмГТУ
УДК 53
ББК 22.3
© ГОУ ВПО «Омский государственный
технический университет», 2009
ВВЕДЕНИЕ
Физика – в своей основе экспериментальная наука. Выявленные ею объективные законы природы получены чаще всего в результате экспериментальных исследований.
Работа в лабораториях физического практикума является частью процесса изучения как физических законов, так и методов, прим



 измерения называется разность между результатом измерения и истинным значением измеряемой величины. Абсолютная погрешность выражается в единицах измеряемой величины.
измерения называется разность между результатом измерения и истинным значением измеряемой величины. Абсолютная погрешность выражается в единицах измеряемой величины. , равная отношению абсолютной погрешности к результату измерения. Относительная погрешность может быть выражена в процентах, она характеризует точность измерений (чем меньше величина относительной погрешности, тем выше точность измерений).
, равная отношению абсолютной погрешности к результату измерения. Относительная погрешность может быть выражена в процентах, она характеризует точность измерений (чем меньше величина относительной погрешности, тем выше точность измерений).



 . Необходимо определить доверительный интервал, в пределах которого с заданной доверительной вероятностью (надежностью) лежит истинное значение диаметра цилиндра.
. Необходимо определить доверительный интервал, в пределах которого с заданной доверительной вероятностью (надежностью) лежит истинное значение диаметра цилиндра.
 .
.

 .
.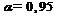 . По таблице определяем значение коэффициента Стьюдента
. По таблице определяем значение коэффициента Стьюдента 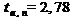 (при
(при  и
и  :
: .
. , даваемую штангенциркулем:
, даваемую штангенциркулем: .
.
 .
.
 .
. ,
,  и
и  ,
,
 и измеренному многократно диаметру
и измеренному многократно диаметру  :
:  (погрешность диаметра определялась с надежностью
(погрешность диаметра определялась с надежностью  .
.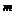 легко логарифмируется.
легко логарифмируется.
 и находим частные производные по соответствующим переменным:
и находим частные производные по соответствующим переменным: .
.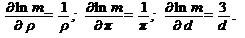
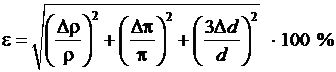


 принимаем равной 0,5 единицы наименьшего разряда числа
принимаем равной 0,5 единицы наименьшего разряда числа  , т.е.
, т.е. 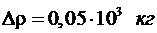 . Погрешность числа
. Погрешность числа  также принимаем равной 0,5 единицы наименьшего разряда числа 3.14, т. е.
также принимаем равной 0,5 единицы наименьшего разряда числа 3.14, т. е.  ).
). , воспользовавшись формулой (20):
, воспользовавшись формулой (20): .
. .
.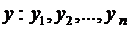 , соответствующих значениям аргумента
, соответствующих значениям аргумента 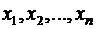 , и необходимо построить график зависимости
, и необходимо построить график зависимости 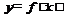 .
. зависит от
зависит от 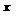 по линейному или квадратичному закону). Однако экспериментальные точки вследствие неизбежных погрешностей, возникающих при измерениях, имеют разброс относительно ожидаемой графической зависимости.
по линейному или квадратичному закону). Однако экспериментальные точки вследствие неизбежных погрешностей, возникающих при измерениях, имеют разброс относительно ожидаемой графической зависимости.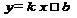 . (21)
. (21) и соответствующих вычисленных значений
и соответствующих вычисленных значений 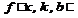 является минимальной.
является минимальной. и
и 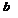 выбирают так, чтобы сумма была минимальной:
выбирают так, чтобы сумма была минимальной: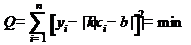 .
. выполняется, если равны нулю частные производные
выполняется, если равны нулю частные производные  и
и  :
: ,
,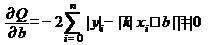 .
. , (22)
, (22)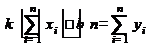 . (23)
. (23) , (24)
, (24)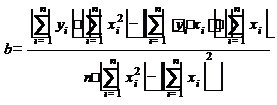 . (25)
. (25)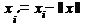 ;
; 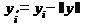 ,
,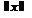 и
и 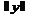 определяются соответственно как
определяются соответственно как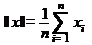 ,
,  ,
,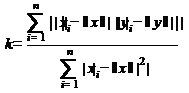 , (26)
, (26)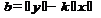 . (27)
. (27)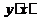 проходит через начало координат, т.е. ожидаемую зависимость можно представить в виде
проходит через начало координат, т.е. ожидаемую зависимость можно представить в виде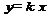 , (28)
, (28) . (29)
. (29)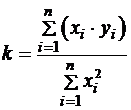 . (30)
. (30) , (31)
, (31) . (32)
. (32) ,
, 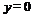 , вычисляют среднеквадратичную погрешность определения только параметра
, вычисляют среднеквадратичную погрешность определения только параметра 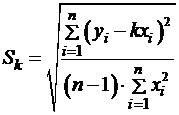 . (33)
. (33) , (34)
, (34)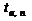 – коэффициент Стьюдента для надежности
– коэффициент Стьюдента для надежности 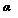 и числа пар точек
и числа пар точек 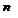 .
.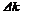 , с которой этот коэффициент определён. Построить наилучшую прямую.
, с которой этот коэффициент определён. Построить наилучшую прямую.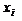
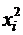
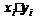
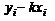
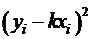
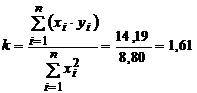
 .
.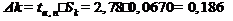 .
.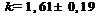 при доверительной вероятности
при доверительной вероятности 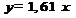 .
. 7) Поскольку зависимость
7) Поскольку зависимость 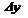 равна:
равна: ,
,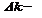 абсолютная погрешность определения параметра
абсолютная погрешность определения параметра  этого распределения имеет вид:
этого распределения имеет вид: . (36)
. (36)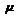 в (36) называется математическим ожиданием, а
в (36) называется математическим ожиданием, а  − дисперсией случайной величины (определения
− дисперсией случайной величины (определения 
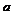 случайной величины
случайной величины  , по оси ординат − плотность вероятности. Функция плотности
, по оси ординат − плотность вероятности. Функция плотности 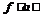 представляет колоколообразную симметричную кривую, имеющую максимум при
представляет колоколообразную симметричную кривую, имеющую максимум при 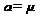 , а точки
, а точки  являются точками перегиба. График нормального закона распределения зависит от параметра
являются точками перегиба. График нормального закона распределения зависит от параметра  . Чем больше
. Чем больше  , равна единице. Расчеты показывают, что вероятность того, что значение случайной величины
, равна единице. Расчеты показывают, что вероятность того, что значение случайной величины  равна
равна 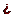 68 %. Это значит, что почти в 70 % случаев значение величины
68 %. Это значит, что почти в 70 % случаев значение величины 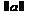 , и для непрерывного распределения оно равно значению интеграла:
, и для непрерывного распределения оно равно значению интеграла: .
.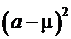 , и для непрерывного распределения оно равно значению интеграла:
, и для непрерывного распределения оно равно значению интеграла: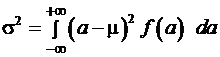 .
.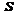 :
: .
. при
при 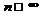 вообще совпадает с
вообще совпадает с  называется стандартным отклонением значения
называется стандартным отклонением значения 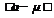 в (36) – это величина погрешности, следовательно, значение функции (35), записанное для
в (36) – это величина погрешности, следовательно, значение функции (35), записанное для 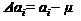 , является плотностью вероятности появления данной погрешности. Соответствующий закон распределения запишется в виде:
, является плотностью вероятности появления данной погрешности. Соответствующий закон распределения запишется в виде: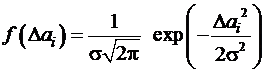 . (37)
. (37) . Это значит, что, когда плотность вероятности появления той или иной погрешности подчиняется нормальному закону, малые погрешности являются более вероятными, чем большие.
. Это значит, что, когда плотность вероятности появления той или иной погрешности подчиняется нормальному закону, малые погрешности являются более вероятными, чем большие.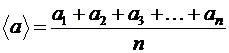 будет стремиться к нормальному распределению с тем же математическим ожиданием
будет стремиться к нормальному распределению с тем же математическим ожиданием 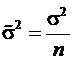 .
.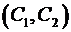 , можно найти с помощью соотношения:
, можно найти с помощью соотношения: . (38)
. (38)
 число измерений;
число измерений;  доверительная вероятность, или надежность.
доверительная вероятность, или надежность.


