

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...
Топ:
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Интересное:
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Дисциплины:
|
из
5.00
|
Заказать работу |
Рассмотрим равновесие малого элементарного параллелепипеда с размерами вдоль осей X и Y соответственно ∆ х, ∆ у, b и толщиной, равной единице.
Обозначим площадки, на которых действуют напряжения, индексами 1,2,3,4. С учетом изменения напряжений в пространстве, напряжения, например, sx для граней 1 и 3, не строго равны друг другу. Символы sx, sу, txy, относятся к т. О (x,y) в центре прямоугольника на рис. 2.9.

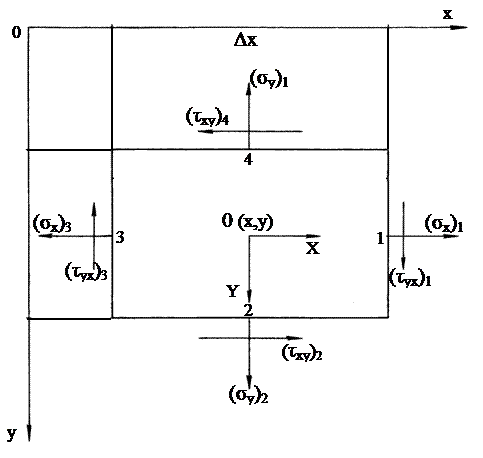
Рис. 2.9. К выводу дифференциальных уравнений равновесия в
системе прямоугольных координат
Значения напряжений посередине граней будем обозначать через (sx)1, (sx)3, и т.д. Поскольку грани прямоугольника малы, то усилия, приложенные к ним, определятся путем умножения соответствующих напряжений на площадь граней, по которым они действуют. Массовые силы в данном случае имеют тот же порядок, что и напряжения. Обозначим компоненты массовых сил через X и Y, тогда уравнение равновесия сил, действующих параллельно оси X, будет иметь вид:
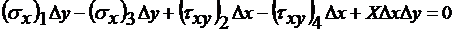 ,
,
или, после деления всех членов уравнения на  ,
,
 . (2.25)
. (2.25)
Если теперь уменьшить размеры элементарного параллелепипеда, положив  ®0 и
®0 и 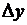 ®0, то, согласно определению производной, предел выражения
®0, то, согласно определению производной, предел выражения 
 будет равен
будет равен 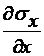 , а второй член уравнения (2.25) станет равным
, а второй член уравнения (2.25) станет равным  . Аналогичные выражения получим, проецируя все силы на ось Y.
. Аналогичные выражения получим, проецируя все силы на ось Y.
Таким образом, будем иметь

(2.26)

Это и есть два дифференциальных уравнения равновесия для двухмерной плоской задачи.
Практически во всех задачах геомеханики единственной массовой силой является вес горных пород. Тогда, направив ось Y вниз и обозначив через γ объемный вес горных пород ( ), получим уравнения равновесия в следующем виде:
), получим уравнения равновесия в следующем виде:
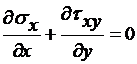 ;
;  . (2.27)
. (2.27)
Очень многие задачи механики горных пород удобно решать в полярной системе координат (r, q), в которой компоненты напряжений имеют обозначения sr,sq и trq. (рис. 2.10).
Между напряжениями, записанными в полярной и прямоугольной системе координат, существуют следующие функциональные соотношения

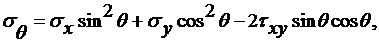 (2.28)
(2.28)
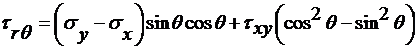 .
.

Рис. 2.10. К выводу дифференциальных уравнений равновесия в полярных координатах
Подставляя (2.28) в (2.27), получим дифференциальное уравнение равновесия в полярной системе координат

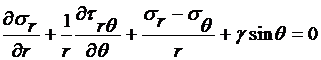 ,
,
(2.29)
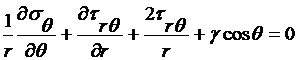 .
.
В случае полярно-симметричной задачи (trq=0) и при отсутствии массовых сил (γ=0) уравнения равновесия (2.29) сводятся к одному, более простому
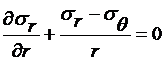 . (2.30)
. (2.30)
Граничные условия
Уравнения равновесия должны удовлетворяться во всех точках исследуемого тела. При достижении границ области компоненты напряжений должны быть такими, чтобы они находились в равновесии с внешними силами, приложенными к границе. В силу этого внешние силы можно рассматривать как продолжение внутренних напряжений.
Рассмотрим малую треугольную призму, такую, что ее гипотенуза совпадает с границей тела (рис 2.11). Обозначим через  и
и  компоненты поверхностных сил Р, отнесенных к единице поверхности в этой точке границы. Уравнения равновесия будут иметь вид:
компоненты поверхностных сил Р, отнесенных к единице поверхности в этой точке границы. Уравнения равновесия будут иметь вид:
 ,
,  , (2.31)
, (2.31)
где l, m – направляющие косинусы нормали  к границе.
к границе.

В частном случае рассмотрения равновесия прямоугольной пластинки координатные оси обычно направляют параллельно граням пластинки и граничные условия (2.31) можно упростить. Пусть, например, одна из сторон пластинки параллельна оси X, тогда нормаль  на этой части границы будет параллельна оси Y; отсюда l =0, m =1. Уравнения (2.31) в этом случае примут вид:
на этой части границы будет параллельна оси Y; отсюда l =0, m =1. Уравнения (2.31) в этом случае примут вид:
 ;
;  (2.32)
(2.32)
причем знак (+) берется в том случае, если нормаль  проведена в сторону положительных значений y; в противном случае берется знак (-). Из последних формул видно, что компоненты напряжений на границе равны компонентам поверхностных усилий, отнесенных к единице площади границы.
проведена в сторону положительных значений y; в противном случае берется знак (-). Из последних формул видно, что компоненты напряжений на границе равны компонентам поверхностных усилий, отнесенных к единице площади границы.

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!