Т еория напряжений. Принимая во внимание гипотезу об однородности и непрерывном распределении вещества, выделим в деформированном породном массиве, который находится в равновесии, произвольную точку А (x, y, z).
Мысленно рассечем рассматриваемый массив плоскостью, проходящей через точку А на две части и отбросим одну из них (рис. 2.3.).  При этом для того, чтобы оставшаяся часть осталась в состоянии равновесия к плоскости сечения необходимо приложить некоторые внутренние силы pν, распределенные по этому сечению и отражающие действие отброшенной части породного массива на оставшуюся. Величина, характеризующая интенсивность распределения внутренних сил, называется напряжением.
При этом для того, чтобы оставшаяся часть осталась в состоянии равновесия к плоскости сечения необходимо приложить некоторые внутренние силы pν, распределенные по этому сечению и отражающие действие отброшенной части породного массива на оставшуюся. Величина, характеризующая интенсивность распределения внутренних сил, называется напряжением.
Выделим в окрестности точки А элемент ∆F площади сечения. Пусть ν – внешняя нормаль к элементу площади ∆F. Обозначим углы, образованные нормалью с осями координат через αx, αy, αz. Косинусы этих углов называются направляющими и обозначаются, соответственно, через l, m, n. Внутренние силы рν заменим главным вектором ∆Pν, приложенным в точке А. Отношение ∆Pν к ∆F характеризует среднюю интенсивность распределения внутренних сил по рассматриваемой элементарной площадке. При стремлении ∆F к нулю предел отношения имеет вполне определенное значение, называемое полным напряжением pν в точке А по площадке с нормалью ν:
 . (2.2)
. (2.2)
Для дальнейшего рассмотрения целесообразно ввести в рассмотрение две составляющие полного напряжения рν: проекцию вектора Pν на нормаль ν к площадке, т.е. нормальное напряжение σν, и проекцию вектора Pν на плоскость элементарной площадки ∆Fi – касательное напряжение τν.
Очевидно, что через точку А можно провести множество различно ориентированных площадок ∆Fi. Каждой из площадок соответствует свой вектор полного напряжения Рνi. Совокупность векторов напряжений во всех площадках, проходящих через рассматриваемую точку, полностью характеризует напряженное состояние в этой точке.
Напряженное состояние в точке А может быть определено также заданием векторов напряжений Рx, Рy, Рz в трех взаимноперпендикулярных площадках, проходящих через это точку (рис. 2.4). Пересекаясь, эти площадки образуют некоторую прямоугольную систему координат.

Рис. 2.4. Обозначение компонентов напряжения на косой произвольно
ориентированной площадке
Полное напряжение, например, Px в координатной плоскости y0z, т.е. в площадке с нормалью х, в общем случае раскладывается на три напряжения, параллельные осям координат: нормальное напряжение σx и и касательные напряжения τxy, τxz. Эти составляющие называют еще компонентами напряжения. Индексы у касательных напряжений означают: первый – координатную ось, нормальную к рассматриваемой площадке, второй – координатную ось, которой рассматриваемая составляющая касательного напряжения параллельна. Таким образом, имеется три компонента нормального sx, sy и sz и шесть - касательного напряжений - txy, tyx, txz, tzx, tyz, tzy.
Зная величины и направления нормальных и касательных напряжений в трех взамноперпендикулярных площадках, которые принимаются за координатные плоскости, можно вычислить напряжения в любой площадке, проходящей через рассматриваемую точку, если известны направляющие косинусы l, m, n нормали ν к этой площадке по отношению к выбранным осям.
Итак, полное напряжение Pν можно разложить на составляющие, параллельные координатным осям Xν, Yν, Zν. Тогда из условия равновесия пирамиды АВСО получим следующие выражения для составляющих полного напряжения Pν в наклонной грани пирамиды:
 (2.3)
(2.3)
Полное напряжение Pν на наклонной площадке определится через свои составляющие следующим образом:
 (2.4)
(2.4)
Таким образом, напряженное состояние в произвольной точке породного массива считается установленным, если известны девять компонентов напряжений, из которых, в силу закона парности касательных напряжений ( и т.д.) независимыми являются шесть.
и т.д.) независимыми являются шесть.
В геомеханике часто используют иное представление о распределении напряжений в породном массиве. Для этого в окрестности исследуемой точки выделяют прямоугольный параллелепипед, грани которого параллельны координатным плоскостям (рис. 2.5.). На гранях параллелепипеда изображают составляющие компоненты напряжения. Компоненты напряжения на параллельных гранях равны, если расстояние между ними стремится к нулю.

Можно доказать, что напряженное состояние в точке исследуемого тела есть некоторая величина, не зависящая от выбора координатных осей [25]. Эта величина называется тензором напряжения, а компоненты напряженного состояния - компонентами тензора. Более строгое определение понятия «тензор» рассматривается в специальном разделе математики – тензорном исчислении.
Как числа и векторы, тензоры можно складывать, умножать. Так, суммой двух тензоров является новый тензор, компоненты которого равны суммам соответствующих компонент слагаемых тензоров. Умножить тензор на число – значит умножить на это число каждый из его компонент.
Тензор напряжения записывается в форме следующей симметричной матрицы
 . (2.5)
. (2.5)
Если ввести понятие о среднем, или гидростатическом, напряжении
 , (2.6)
, (2.6)
то тензор напряжения можно представить в виде суммы двух составляющих:
 (2.7)
(2.7)
где  - шаровой тензор, равный
- шаровой тензор, равный
 , (2.8)
, (2.8)
и 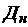 - девиатор напряжений, равный
- девиатор напряжений, равный
 (2.9)
(2.9)
Шаровой тензор в общем напряженном состоянии обеспечивает уменьшение (увеличение) объема деформируемого тела без изменения формы, а девиатор – изменение его формы.
Систему координат всегда можно изменить таким образом, что направления координатных осей совпадут с линиями действия таких нормальных напряжений, при которых касательные напряжения равны нулю. Эти напряжения называют главными и обозначают σ1, σ2, σ3. Причем, подразумевается, что σ1 > σ2 > σ3.
Главные напряжения в точке σ1, σ2, σ3 можно вычислить, зная девять компонент напряжения при произвольной ориентации системы координат. Так, например, для определения величины σ1 следует приравнять нулю определитель
 (2.10)
(2.10)
Развернув этот определитель в строчку, получим кубическое уравнение с одним неизвестным σ1:
 (2.11)
(2.11)
Коэффициенты при 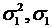 и свободный член в уравнении (2.11) называются, соответственно, первым, вторым и третьим инвариантами тензора напряжения и обозначаются
и свободный член в уравнении (2.11) называются, соответственно, первым, вторым и третьим инвариантами тензора напряжения и обозначаются 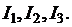
Первый инвариант  называется линейным. Он характеризует изменение объема вещества в окрестности инварианта
называется линейным. Он характеризует изменение объема вещества в окрестности инварианта  и определяет возможность перехода тела в пластическую область. Мизес показал, что пластическая текучесть наступает, если второй инвариант тензора девиатора напряжений достигает некоторой критической величины, характерной для данного тела:
и определяет возможность перехода тела в пластическую область. Мизес показал, что пластическая текучесть наступает, если второй инвариант тензора девиатора напряжений достигает некоторой критической величины, характерной для данного тела:
 (2.12)
(2.12)
где 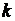 - константа материала, которая равна пределу текучести при чистом сдвиге.
- константа материала, которая равна пределу текучести при чистом сдвиге.
Третий инвариант также имеет определенный физический смысл.
Теория деформаций. Под деформацией породного массива подразумевают изменение взаимного положения его точек. По-прежнему полагаем, что породная среда является сплошной и однородной. Тогда в любой ее точке находится материальная частица. Пусть координаты этой частицы будут x, y, z. В процессе деформирования породной среды рассматриваемая частица получит перемещения u, v, w по направлениям координатных осей x, y, z и в результате будет иметь координаты x+u, y+v, z+ w. В общем случае перемещения u, v, w меняются от точки к точке и поэтому являются функциями координат x, y, z.
Исследование деформаций начнем на примере двухмерной задачи плоской деформации. Под плоской деформацией будем понимать такой частный случай деформированного состояния, при котором все частицы, находившиеся первоначально в одной плоскости, останутся после деформирования в той же плоскости. Предположим, что координатные оси выбраны так, что оси x и y лежат в плоскости деформации. Тогда w=0, а величины u и v не зависят от координат z.
Рассмотрим малый прямоугольный элемент АВСД недеформированной породной среды со стороны dx и dy (рис. 2.6).
После деформации элемент занимает положение А'В'С'Д'. С геометрической точки зрения различают два основных типа деформаций: продольную – изменение первоначальной длины – и деформацию сдвига – изменение величины первоначально прямого угла. Продольная деформация обозначается буквой ε, сдвиговая – γ.
Продольная деформация определяется как предел отношения изменения длины отрезка  к его первоначальной длины
к его первоначальной длины  , т.е.
, т.е.
 (2.13)
(2.13)
или
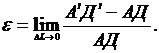 (2.14)
(2.14)

Рис. 2.6. Схема к выводу соотношений между компонентами
Перемещений и деформаций
Выражая длины отрезков А'Д' и АД через U и dx и пренебрегая величинами высшего порядка малости для продольной деформации в направлении оси x, после преобразований получим, что
 (2.15)
(2.15)
Чтобы определить деформацию сдвига, рассмотрим искажение первоначально прямого угла ВАД. Деформация сдвига ху в точке А определится как изменение величины угла между двумя элементарными отрезками АВ и АД, первоначально параллельными осями x и y. Из геометрического рассмотрения получим
 (2.16)
(2.16)
Для трехмерной задачи компоненты деформаций могут быть получены аналогичным образом. Они будут равны:
 . (2.17)
. (2.17)
Эти соотношения известны под названием уравнений Коши. Шесть величин εx, εy, εz, γxy, γyz, γzx, называются компонентами деформации. Деформации сдвига, как следует из (2.17), обладают симметрией, т.е. 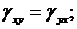
 и т.д.
и т.д.
По аналогии с напряжениями можно ввести в рассмотрение понятие о средней деформации:
 . (2.18)
. (2.18)
Тогда тензор деформации, подобно тензору напряжения, можно также разложить на шаровой тензор деформаций и девиатор деформаций:
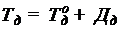 . (2.19)
. (2.19)
Шаровой тензор деформации представляет собой следующую матрицу
 , (2.20)
, (2.20)
а девиатор деформаций, соответственно, равен
 (2.21)
(2.21)
Первый характеризует величину объемного расширения (сжатия), второй - формоизменение объема в окрестности рассматриваемой точки среды.
Связь между напряжениями и деформациями. Все тела, находящиеся в напряженном состоянии, получают деформацию. Зависимость между деформацией и приложений силой впервые была сформулирована Гуком применительно к тонкому стрежню. В случае объемного напряженного состояния закон Гука формулируется следующим образом: в любой точке сплошной среды каждый из шести компонентов напряжений является линейной функцией шести компонентов деформации, и наоборот. Это положение называется обобщенным законом Гука и записывается так:
 ,
,
 , (2.22)
, (2.22)
 .
.
Составляющие тензоров напряжения и деформации связаны между собой следующими линейными зависимостями:
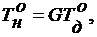 (2.23)
(2.23)
 (2.24)
(2.24)
Выражение (2.23) называют законом упругого изменения объема, а выражение (2.24) - законом упругого изменения формы.
Виды напряженного состояния
Из предыдущего параграфа следует, что в самом общем случае напряженно-деформированное состояние выделенного элементарного объема в окрестности рассматриваемой точки характеризуется наличием девяти компонентов напряжений и девяти компонентов деформаций. Такое напряженно-деформированное состояние, как уже отмечалось, называется объемным.
Решение объемных задач даже только с применением методов теории упругости сопряжено со значительными математическими трудностями. Поэтому решение любой геомеханической задачи начинают с анализа особенностей напряженно-деформированного состояния для того, чтобы упростить исходную расчетную схему и привести ее по возможности к так называемой плоской задаче, когда всего лишь два компонента напряжений и два компонента деформаций зависят от координат точек тела.
Так, например, если тонкую пластину, находящуюся в состоянии равновесия под действием внешних сил, нагрузить равномерно распределенными по толщине усилиями, приложенными к ее границе параллельно плоскости пластины, то компоненты напряжений  на обеих поверхностях пластины будут равны нулю и можно предположить, что они равны нулю и внутри пластины (рис. 2.7). Такое напряженное состояние будет определяться только компонентами напряжений
на обеих поверхностях пластины будут равны нулю и можно предположить, что они равны нулю и внутри пластины (рис. 2.7). Такое напряженное состояние будет определяться только компонентами напряжений  и называется плоским напряженным состоянием. Доказано, что в тонких пластинах все три неизвестные компоненты напряжений не зависят от координаты Z, а являются только функциями координат X и Y.
и называется плоским напряженным состоянием. Доказано, что в тонких пластинах все три неизвестные компоненты напряжений не зависят от координаты Z, а являются только функциями координат X и Y.
Плоское напряженное состояние не является характерным для задач геомеханики. Но упрощения, подобные приведенным выше, возможны и в другом предельном случае, когда размер тела в направлении оси Z очень велик.
Это могут быть, например, подпорная стенка или длинная горизонтальная выработка (рис.2.8.а,б). Очевидно, что если мы будем рассматривать напряженно-деформированное состояние массива вокруг выработки на достаточном удалении от ее торцов, то все сечения, перпендикулярные продольной оси выработки Z, будут находиться в одинаковых условиях.
Рис. 2.8. Плоское деформированное состояние
Компоненты перемещений u и υ не зависят от координаты Z и являются функциями координат X и Y. Продольные перемещения ω при этом равны нулю. Такое напряженное состояние называется плоской деформацией.
Принимая во внимание соотношение (2.18), получим

Продольные напряжения  можно получить, используя закон Гука (2.22).
можно получить, используя закон Гука (2.22).

или
 .
.
Эти нормальные напряжения действуют по всем поперечным сечениям, достаточно удаленным от торцов выработки.
Таким образом, задача о плоской деформации, как и задача о плоском напряженном состоянии, сводится к определению компонентов напряжений  и
и  , как функций X и Y.
, как функций X и Y.
Это обстоятельство, как будет показано далее, существенно упрощает задачу и позволяет получить ее решение в замкнутом виде, то есть в виде конечных формул.
Одноосное напряженное состояние характеризуется одним компонентом напряжений и соответствующим ему компонентом деформации. Оно реализуется в стержневых системах. В задачах механики подземных сооружений такое напряженно-деформированное состояние встречается при расчете конструкций крепи горных выработок, различных ферм, балок.



 При этом для того, чтобы оставшаяся часть осталась в состоянии равновесия к плоскости сечения необходимо приложить некоторые внутренние силы pν, распределенные по этому сечению и отражающие действие отброшенной части породного массива на оставшуюся. Величина, характеризующая интенсивность распределения внутренних сил, называется напряжением.
При этом для того, чтобы оставшаяся часть осталась в состоянии равновесия к плоскости сечения необходимо приложить некоторые внутренние силы pν, распределенные по этому сечению и отражающие действие отброшенной части породного массива на оставшуюся. Величина, характеризующая интенсивность распределения внутренних сил, называется напряжением. . (2.2)
. (2.2)
 (2.3)
(2.3) (2.4)
(2.4) и т.д.) независимыми являются шесть.
и т.д.) независимыми являются шесть.
 . (2.5)
. (2.5) , (2.6)
, (2.6) (2.7)
(2.7) - шаровой тензор, равный
- шаровой тензор, равный , (2.8)
, (2.8)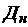 - девиатор напряжений, равный
- девиатор напряжений, равный (2.9)
(2.9) (2.10)
(2.10) (2.11)
(2.11)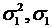 и свободный член в уравнении (2.11) называются, соответственно, первым, вторым и третьим инвариантами тензора напряжения и обозначаются
и свободный член в уравнении (2.11) называются, соответственно, первым, вторым и третьим инвариантами тензора напряжения и обозначаются 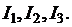
 называется линейным. Он характеризует изменение объема вещества в окрестности инварианта
называется линейным. Он характеризует изменение объема вещества в окрестности инварианта  и определяет возможность перехода тела в пластическую область. Мизес показал, что пластическая текучесть наступает, если второй инвариант тензора девиатора напряжений достигает некоторой критической величины, характерной для данного тела:
и определяет возможность перехода тела в пластическую область. Мизес показал, что пластическая текучесть наступает, если второй инвариант тензора девиатора напряжений достигает некоторой критической величины, характерной для данного тела: (2.12)
(2.12)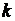 - константа материала, которая равна пределу текучести при чистом сдвиге.
- константа материала, которая равна пределу текучести при чистом сдвиге. к его первоначальной длины
к его первоначальной длины  , т.е.
, т.е. (2.13)
(2.13)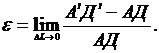 (2.14)
(2.14)
 (2.15)
(2.15) (2.16)
(2.16) . (2.17)
. (2.17)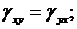
 и т.д.
и т.д. . (2.18)
. (2.18)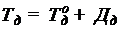 . (2.19)
. (2.19) , (2.20)
, (2.20) (2.21)
(2.21) ,
, , (2.22)
, (2.22) .
.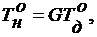 (2.23)
(2.23) (2.24)
(2.24) на обеих поверхностях пластины будут равны нулю и можно предположить, что они равны нулю и внутри пластины (рис. 2.7). Такое напряженное состояние будет определяться только компонентами напряжений
на обеих поверхностях пластины будут равны нулю и можно предположить, что они равны нулю и внутри пластины (рис. 2.7). Такое напряженное состояние будет определяться только компонентами напряжений  и называется плоским напряженным состоянием. Доказано, что в тонких пластинах все три неизвестные компоненты напряжений не зависят от координаты Z, а являются только функциями координат X и Y.
и называется плоским напряженным состоянием. Доказано, что в тонких пластинах все три неизвестные компоненты напряжений не зависят от координаты Z, а являются только функциями координат X и Y.


 можно получить, используя закон Гука (2.22).
можно получить, используя закон Гука (2.22).
 .
. и
и  , как функций X и Y.
, как функций X и Y.

