В критериях Байеса вероятности состояний природы были получены на основании статистических данных изменения состояний природы. Однако часто получить такие данные не представляется возможным. Тогда найти решениезадачи игры с природой в условиях риска позволяет субъективная оценка состояний природы и количественная оценка вероятностей проявления этих состояний. Один из способов заключается в том, что события природы будут равновероятны:
P1= P2 =… =Pn = 1/n.
Этот принцип называют еще принципом «недостаточного основания» Лапласа. Следовательно, показатель эффективности стратегии Ai, будет равен
 i=1,…,m.
i=1,…,m.
Тогда оптимальная стратегия лица А определяется по формуле (3.8). Аналогично рассматривается критерий Лапласа для матрицы рисков.
Задача. Постановка задачи совпадает с постановкой предыдущей задачи.. Найти оптимальную стратегию игрока А по критерию Лапласа, относительно выигрышей.
Решение.
Вычислим показатели эффективности для каждой стратегии игрока А:
a1 = 0,25·(25+35+40+20) = 30;
a2 = 0,25·(70+20+4-30+25) = 36.25;
a3 = 35·0.2+85·0.3+20·0.4+30·0.1 = 42.5;
a4 = 80·0.2+10·0.3+35·0.4+40·0.1 =41,25;
Максимальный выигрыш равен
a*= max (30; 36,25; 42,5;41,25) = 42,5
Максимальный выигрыш по критерию Лапласа достигается при использовании игроком А стратегии А3.
Глава 3. Задания для выполнения контрольной работы
Контрольная работа по дисциплине «Теория игр» состоит из трех задач по различным темам курса. При оформлении работы следует привести подробное решение каждой задачи указанным в условии способом и сделать обоснованные экономические выводы. Численное решение примеров следует подкрепить использованием компьютерных технологий (где это возможно).
Номер варианта контрольной работы определяется по последней цифре номера личного дела (зачетной книжки).
3.1. Порядок выполнения и оформления контрольной работы
Контрольная работа выполняется и защищается в установленные преподавателем сроки.
Титульный лист контрольной работы должен содержать все необходимые реквизиты:
- названия университета и филиала;
- название кафедры;
- направление подготовки;
- наименование учебной дисциплины;
- Ф.И.О. студента и номер его зачетной книжки;
- Ф.И.О. преподавателя;
- дату сдачи работы на проверку.
Решение заданий контрольной работы следует сопровождать необходимыми комментариями, т.е. все основные этапы решения задачи должны быть раскрыты и обоснованы на основе соответствующих теоретических положений. При решении задач целесообразно использование компьютерных программ.
К собеседованию допускаются студенты, выполнившие правильно и в достаточном объеме все задания контрольной работы. Для получения зачета по результатам собеседования студент должен выполнить работу над ошибками в проверенной преподавателем контрольной работе, знать теоретические основы методов решения всех заданий и уметь ответить на конкретные вопросы, связанные с последовательностью решения.
Задания контрольной работы
Задача 1
С учетом вариантов  сложившегося на рынке поведения покупателей в микрорайоне города коммерческое предприятие разработало несколько технологий продажи товаров
сложившегося на рынке поведения покупателей в микрорайоне города коммерческое предприятие разработало несколько технологий продажи товаров  . Возможные варианты среднедневного товарооборота (в млн. руб.) в зависимости от различных сочетаний
. Возможные варианты среднедневного товарооборота (в млн. руб.) в зависимости от различных сочетаний  и
и  приведены в матрицах:
приведены в матрицах:
Матрица 1
| Игроки
| В1
| В2
| В3
| В4
|
| А1
| 12 + t
| 20 + v
| 15 + u
| 12 + t
|
| А2
| 12 + t
| 15 + u
| 7 + v
| 3 + u
|
| А3
| 3 + u
| 3 + u
| 12 + t
| 15 + u
|
| А4
| s
| 20 + v
| 7 + v
| 7 + v
|
Матрица 2
| Игроки
| В1
| В2
| В3
| В4
|
| А1
| 4 + v
| 8 + t
| s
| 11 + u
|
| А2
| s
| 4 + v
| 16 + v
| 11 + u
|
| А3
| 4 + v
| 8 + t
| 11 + u
| s
|
| А4
| 11 + u
| 4 + v
| 4 + v
| 4 + v
|
Матрица 3
| Игроки
| В1
| В2
| В3
| В4
| B5
|
| А1
| u + 2
| v + 6
| u + 2
| t + 10
| v + 17
|
| А2
| t – 2
| v + 17
| t – 2
| u + 14
| v + 6
|
| А3
| s – 6
| v + 6
| t – 2
| u + 2
| v + 6
|
| А4
| u + 2
| v + 6
| u + 2
| t + 10
| t + 10
|
Значения параметров, входящих в матрицы:
Требуется:
1) Определить верхние и нижние значения товарооборота коммерческого предприятия.
2) Найти седловую точку игры, если она есть. Используя оптимальные чистые стратегии и чистую цену игры, сделайте выводы экономического характера.
Задача 2
Найти оптимальную смешанную стратегию руководителя коммерческого предприятия (игрок А) и гарантированный средний выигрыш при выборе из двух новых технологий продажи товаров 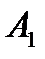 и
и  , если известны выигрыши каждого вида продажи по сравнению со старой технологией (игрок В), которые представлены в виде матрицы:
, если известны выигрыши каждого вида продажи по сравнению со старой технологией (игрок В), которые представлены в виде матрицы:
| Игрок А
| Игрок В
|
| B1
| B2
|
| A1
| a11
| a12
|
| A2
| a21
| a22
|
Элементы матрицы заданы в таблице 1.
Таблица 1
| № варианта
| а11
| а12
| а21
| а22
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 3
Найти решения матричных игр графоаналитическим методом.
А) Сельскохозяйственное предприятие имеет возможность выращивать две культуры. Прибыль предприятия от реализации выращенной культуры зависит от объема полученного урожая. Урожай первой культуры выше при сухой погоде, а второй выше при более влажной. Состояние погоды в летний период можно рассматривать как следующие стратегии природы (игрок В):
1)  – лето жаркое сухое;
– лето жаркое сухое;
2)  – лето жаркое влажное;
– лето жаркое влажное;
3)  – лето теплое влажное;
– лето теплое влажное;
4)  – лето теплое сухое;
– лето теплое сухое;
5)  – лето прохладное.
– лето прохладное.
Стратегии предприятия (игрок А):
1) 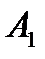 – выращивать первую культуру;
– выращивать первую культуру;
2)  – выращивать вторую культуру.
– выращивать вторую культуру.
Расчеты прибыли предприятия (в млн руб.) в зависимости от состояния погоды приведены в матрицах, соответствующих каждому варианту (таблица 2):
Таблица 2
| Варианты
| Стратегии
игрока А
| Стратегии игрока В
|
| В1
| В2
| В3
| В4
| В5
|
|
| А1
|
|
|
|
|
|
| А2
|
|
|
|
|
|
|
| А1
|
|
|
|
|
|
| А2
|
|
|
|
|
|
|
| А1
|
|
|
|
|
|
| А2
|
|
|
|
|
|
|
| А1
|
|
|
|
|
|
| А2
|
|
|
|
|
|
|
| А1
|
|
|
|
|
|
| А2
|
|
|
|
|
|
|
| А1
|
|
|
|
|
|
| А2
|
|
|
|
|
|
|
| А1
|
|
|
|
|
|
| А2
|
|
|
|
|
|
|
| А1
|
|
|
|
|
|
| А2
|
|
|
|
|
|
|
| А1
|
|
|
|
|
|
| А2
|
|
|
|
|
|
|
| А1
|
|
|
|
|
|
| А2
|
|
|
|
|
|
Требуется определить оптимальные стратегии поведения сельскохозяйственного предприятия и его гарантированный выигрыш.
В) Сельскохозяйственное предприятие (игрок А) должно выращивать определенную культуру, например картофель, на отведенном для этой цели участке. Урожайность картофеля зависит от количества внесенных удобрений и от состояния погоды. Рассматриваются два возможных характера погоды (игрок В):
1)  – лето сухое;
– лето сухое;
2)  – лето влажное.
– лето влажное.
Возможные варианты внесения удобрений:
1) 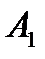 – количество удобрений на 1 га соответствует определенной норме (норму принять равной 1);
– количество удобрений на 1 га соответствует определенной норме (норму принять равной 1);
2)  – количество удобрений на 30 % выше нормы;
– количество удобрений на 30 % выше нормы;
3)  – количество удобрений на 40 % ниже нормы;
– количество удобрений на 40 % ниже нормы;
4)  – количество удобрений на 5 % ниже нормы.
– количество удобрений на 5 % ниже нормы.
Предприятие произвело расчет прибыли в зависимости от возможных стратегий своих и природы. Матрицы прибылей для различных вариантов задачи представлены в таблице:
| Игрок А
| Номер варианта
|
|
|
|
|
|
|
|
|
|
|
|
| Игрок В
|
| В1
| В2
| В1
| В2
| В1
| В2
| В1
| В2
| В1
| В2
| В1
| В2
| В1
| В2
| В1
| В2
| В1
| В2
| В1
| В2
|
| А1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| А2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| А3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| А4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Требуется определить оптимальное количество внесения удобрений и гарантированную прибыль предприятия при любой погоде.
Учебно-методическое и информационное обеспечение дисциплины
Литература
а) основная:
- Конюховский, П. В. Теория игр: учебник для академического бакалавриата / П. В. Конюховский, А. С. Малова. — М.: Издательство Юрайт, 2015. — 252 с. — Серия: Авторский учебник.
- Лабскер Л.Г., Ященко Н.А.: Теория игр в экономике. Практикум с решением задач. Учебное пособие. Издательство: Кнорус, 2014 г. Серия: Бакалавриат. ISBN: 978-5-406-01230-7, 264 стр.
3. Шагин, В. Л. Теория игр: учебник и практикум для академического бакалавриата / В. Л. Шагин. — М.: Издательство Юрайт, 2016. — 223с. — Серия: Авторский учебник.
б) дополнительная:
4. Мазалов, В.В. Математическая теория игр и приложения. [Электронный ресурс] — Электрон.дан. — СПб.: Лань, 2016. — 448 с. — Режим доступа: http://e.lanbook.com/book/76829
5. Захаров, А. В. Теория игр в общественных науках [Текст]: учебник для вузов / А. В. Захаров; Нац. исслед. ун-т «Высшая школа экономики». — М.: Изд. дом Высшей школы экономики, 2015. — (Учебники Высшей школы экономики). — 304 с.— ISBN 978-5-7598-1180-0 (в пер.).
Электронные ресурсы
1. Интернет-репозиторий образовательных ресурсов. – URL: http://repozitory.vzfei.ru. Доступ по логину и паролю.
2. Электронно-библиотечная система (ЭБС) (доступ через интернет-репозиторий образовательных ресурсов). – URL: http://repozitory.vzfei.ru.Доступ по логину и паролю.
3. Федеральная ЭБС «Единое окно доступа к образовательным ресурсам». – URL: http://window.edu.ru. Доступ свободный.
Программное обеспечение
1. Электронная таблица ExcelMSOffice.
2. Программный продукт MatLab.



 i=1,…,m.
i=1,…,m. сложившегося на рынке поведения покупателей в микрорайоне города коммерческое предприятие разработало несколько технологий продажи товаров
сложившегося на рынке поведения покупателей в микрорайоне города коммерческое предприятие разработало несколько технологий продажи товаров  . Возможные варианты среднедневного товарооборота (в млн. руб.) в зависимости от различных сочетаний
. Возможные варианты среднедневного товарооборота (в млн. руб.) в зависимости от различных сочетаний 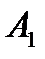 и
и  , если известны выигрыши каждого вида продажи по сравнению со старой технологией (игрок В), которые представлены в виде матрицы:
, если известны выигрыши каждого вида продажи по сравнению со старой технологией (игрок В), которые представлены в виде матрицы: – лето жаркое сухое;
– лето жаркое сухое; – лето жаркое влажное;
– лето жаркое влажное; – лето теплое влажное;
– лето теплое влажное; – лето теплое сухое;
– лето теплое сухое; – лето прохладное.
– лето прохладное. – количество удобрений на 40 % ниже нормы;
– количество удобрений на 40 % ниже нормы; – количество удобрений на 5 % ниже нормы.
– количество удобрений на 5 % ниже нормы.

