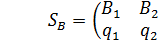Рассмотрим конечную матричную игру размерности (mxn) c платежной матрицей А = (аij), все элементы которой положительны. Будем считать, что данная игра не имеет решения в чистых стратегиях (нет седловой точки). Следовательно, оптимальное решение необходимо искать в смешанных стратегиях.
Пусть игроки А и В обладают следующими смешанными стратегиями:
 ,
, 
Постановка задачи для игрока А.
Исследовать на min целевую функцию
 (1.7)
(1.7)
при ограничениях:
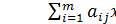 j=1,…,n, (1.8)
j=1,…,n, (1.8)
 , i=1,…,m.
, i=1,…,m.
Здесь  .
.
Постановка задачи для игрока В.
Исследовать на max целевую функцию
 (1.9)
(1.9)
при ограничениях:
 i=1,…,m, (1.10)
i=1,…,m, (1.10)
 , j=1,…,n
, j=1,…,n
Здесь  ,
,
После решения пары двойственных задач находим оптимальные смешанные стратегии игроков А и В:
 , (1.11)
, (1.11)
и определяем цену игры
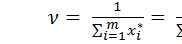 , (1.12)
, (1.12)
где i=1,…,m и j=1,…,n.
Алгоритм решения конечной матричной игры путем сведения ее к паре двойственных задач:
1) Если среди элементов платежной матрицы есть отрицательные, то ко всем элементам прибавим одно и тоже положительное число k, чтобы все элементы стали положительными
2) Сводим конечную матричную игру к паре двойственных задач и находим их решения:  .
.
3) рассчитываем оптимальные смешанные стратегии игроков
 ,
,
4) находим цену игры

Задача.
Дана конечная матричная игра с платежной матрицей вида:

Переходя к задаче ЛП определить оптимальные стратегии игроков и цену игры.
Решение.
1) Решение в чистых стратегиях
Имеем,  ,
,  . Так как α< β, игра не имеет решения в чистых стратегиях, так как седловой точки нет.
. Так как α< β, игра не имеет решения в чистых стратегиях, так как седловой точки нет.
2) Решение в смешанных стратегиях.
Найти смешанные стратегии игроков:
 ,
, 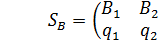
Задача для игрока А Задача для игрока B
Целевая функция Целевая функция
F(x)=x1+ x2+7x3 → min f(x)=y1+ y2+y3 → max
Ограничения: Ограничения:
3x1+9 x2+7x3 ≥ 1 3y1+6 y2+8y3 ≤ 1
6x1+4 x2+5x3 ≥ 1 9y1+4 y2+2y3 ≤ 1
8x1+2x2+4x3 ≥ 1 7y1+5 y2+4y3 ≤ 1
xi ≥ 0, i=1,…,3 yj≥ 0, j=1,…,3
Решая эти задачи в среде табличного процессора Excel, используя симплексный метод в опции «Поиске решений», находим:
| Решение для игрока А
| Решение для игрока В
|
| Неизвестные:
| | Неизвестные:
| |
| x1=
| 0,074074
| | y1=
| 0,037037
| |
| x2=
|
| | y2=
| 0,148148
| |
| x3=
| 0,111111
| | y3=
|
| |
| | | | | | |
| | | | | | |
| Целевая функция (min):
| Целевая функция (max):
|
| f=x1+x2+x3
| 0,185185
| | F=y1+y2+y3
| 0,185185
| |
| | | | | | |
| Ограничения:
| | Ограничения:
| |
| _>1
|
| | <1
|
| |
| _>1
|
| | <1
| 0,925926
| |
| _>1
| 1,037037
| | <1
|
| |
| | | | | | |
| Оптимальное решение A:
| Оптимальное решение B:
|
| р1=x1/f
| 0,4
| | q1=y1/F
| 0,2
| |
| р2=x2/f
|
| | q2=y2/F
| 0,8
| |
| р3=x3/f
| 0,6
| | q3=y3/F
|
| |
| ν=1/f
| 5,4
| | ν=1/F
| 5,4
| |
Игры с природой
Понятие игры с природой
Рассмотренные выше матричные и биматричные игры и методы их решения предполагали многократные повторения решений с некоторыми вероятностями (частотами) применения выбранных стратегий игроками. На практике при решении экономических задач, которые сводятся к игровым моделям, количество принимаемых управленческих решений ограничено, а нередко вообще принимается однократно в условиях неопределенности и риска.
В игровых задачах, которые моделирую экономические процессы с такого рода неопределенностью, принятие решения зависит от состояния объективной действительности, которую принято называть «природой». Следовательно, в игре с природой осознанно действует только один игрок, лицо принимающее решение. Второй игрок - природа, которая осознанно против первого игрока не действует, принимая то или иное состояние произвольным образом, конкретных целей в игре не преследует и безразлична к результату игры. Поэтому термин «природа» характеризует некоторую реальность – политика, финансы, промышленность, сельское хозяйство и т.п., которая в задачах будет провялятся в конкретных формах.
Математическая модель игр с природой следующая. Пусть игрок А (ЛПР) имеет m стратегий Ai, i=1,…,m, а природа Q может находится в одном из n возможных состояний Qj, j=1,…,n, которые можно рассматривать как ее стратегии. Тогда платежную матрицу игры с природой можно представить в виде, аналогичном платежной матрицы А = (aij)mxn, или
|
| Q1
| Q2
| …
| Qn
|
| A1
| a11
| a12
| …
| a1n
|
| A2
| a21
| a21
| …
| a2n
|
| …
| …
| …
| …
| …
|
| Am
| am1
| am2
| …
| amn
|
Здесь aij – выигрыши игрока А при выборе стратегии Аi и при состоянии природы Qj. Матрица игры с природой содержательно отличается от платежной матрицы антагонистической игры тем, что элементы столбцов данной матрицы не являются проигрышами природы при соответствующих ее состояниях, а это оценка эффективности стратегии ЛПР при данных состояниях природы.



 ,
, 
 (1.7)
(1.7)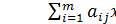 j=1,…,n, (1.8)
j=1,…,n, (1.8) , i=1,…,m.
, i=1,…,m. .
. (1.9)
(1.9) i=1,…,m, (1.10)
i=1,…,m, (1.10) , j=1,…,n
, j=1,…,n ,
, , (1.11)
, (1.11)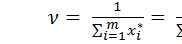 , (1.12)
, (1.12) .
. ,
,

 ,
,  . Так как α< β, игра не имеет решения в чистых стратегиях, так как седловой точки нет.
. Так как α< β, игра не имеет решения в чистых стратегиях, так как седловой точки нет. ,
,