|
Вербальная форма
|
Графическая форма
|
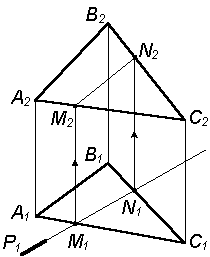
1. Для построения линии пересечения двух плоскостей Р(Р1) и Q(D АВС) необходимо определить две точки M и N – общие для этих плоскостей. Видно, что горизонтальная проекция плоскости Р1 совпадает с горизонтальной проекцией линии пересечения плоскостей Р и Q.
M1N1 = P1  Q1 Q1
| 
|
2. Строим фронтальную проекцию линии пересечения плоскостей
M2N2 = P2  Q2 Q2
| 
|
| 3. Определяем видимость. Часть плоскости Q (D АВС) не видима, так как она расположена за плоскостью Р
| 
|
12.Ортогональная проекция прямого угла.
Ортогональное (прямоугольное) проецирование есть частный случай проецирования параллельного, когда все проецирующие лучи перпендикулярны плоскости проекций. Ортогональным проекциям присущи все свойства параллельных проекций, но при прямоугольном проецировании проекция отрезка, если он не параллелен плоскости проекций, всегда меньше самого отрезка (рис. 58). Это объясняется тем, что сам отрезок в пространстве является гипотенузой прямоугольного треугольника, а его проекция — катетом: А'В' = ABcos a.
При прямоугольном проецировании прямой угол проецируется в натуральную величину, когда обе стороны его параллельны плоскости проекций, и тогда, когда лишь одна из его сторон параллельна плоскости проекций, а вторая сторона не перпендикулярна этой плоскости проекций.
Теорема о проецировании прямого угла. Если одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпенди-

Рис. 58
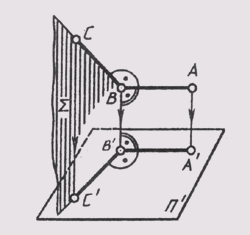
Рис. 59
кулярна, то при ортогональном проецировании прямой угол проецируется на эту плоскость в прямой же угол.
Пусть дан прямой угол ABC, у которого сторона АВ параллельна плоскости п' (рис. 59). Проецирующая плоскость перпендикулярна плоскости п'. Значит, АВ _|_S, так как АВ _|_ВС и АВ _|_ВВ, отсюда АВ _|_В'С'. Но так какАВ || А'В' _|_ В'С', т. е. на плоскости п' угол между А'В' и В'С равен 90°.
Обратимость чертежа. Проецирование на одну плоскость проекций дает изображение, которое не позволяет однозначно определить форму и размеры изображенного предмета. Проекция А (см. рис. 53) не определяет положение самой точки в пространстве, так как не известно, на какое расстояние она удалена от плоскости проекций п'. Любая точка проецирующего луча, проходящего через точку А, будет иметь своей проекцией точку А'. Наличие одной проекции создает неопределенность изображения. В таких случаях говорят о необратимости чертежа, так как по такому чертежу невозможно воспроизвести оригинал. Для исключения неопределенности изображение дополняют необходимыми данными. В практике применяют различные способы дополнения однопроекционного чертежа. В данном курсе будут рассмотрены чертежи, получаемые ортогональным проецированием на две или более взаимно перпендикулярные плоскости проекций (комплексные чертежи) и путем перепроецирования вспомогательной проекции предмета на основную аксонометрическую плоскость проекций (аксонометрические чертежи).
13.Взаимно перпендикулярные прямые и плоскости.
Определение
Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна каждой прямой, которая лежит в данной плоскости и проходит через точку пересечения.

Теорема 1
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ.
Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.
Доказательство:
Пусть а прямая, перпендикулярная прямым b и c в плоскости 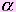 . Тогда прямая а проходит через точку А пересечения прямых b и c. Докажем, что прямая а перпендикулярна плоскости
. Тогда прямая а проходит через точку А пересечения прямых b и c. Докажем, что прямая а перпендикулярна плоскости 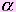 .
.
Проведем произвольную прямую х через точку А в плоскости 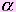 и покажем, что она перпендикулярна прямой а. Проведем в плоскости
и покажем, что она перпендикулярна прямой а. Проведем в плоскости 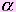 произвольную прямую, не проходящую через точку А и пересекающую прямые b, c и х. Пусть точками пересечения будут В, С и Х.
произвольную прямую, не проходящую через точку А и пересекающую прямые b, c и х. Пусть точками пересечения будут В, С и Х.
Отложим на прямой а от точки А в разные стороны равные отрезки АА1 и АА2. Треугольник А1СА2 равнобедренный, так как отрезок АС является высотой по условию теоремы и медианой по построению (АА1 = АА2).по той же причине треугольник А1ВА2 тоже равнобедренный. Следовательно, треугольники А1ВС и А2ВС равны по трем сторонам.
Из равенства треугольников А1ВС и А2ВС следует равенство углов А1ВХ и А2ВХ и, следовательно равенство треугольников А1ВХ и А2ВХ по двум сторонам и углу между ними. Из равенства сторон А1Х и А2Х этих треугольников заключаем, что треугольник А1ХА2 равнобедренный. Поэтому его медиана ХА является также высотой. А это и значит, что прямая х перпендикулярна а. По определению прямая а перпендикулярна плоскости 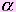 . Теорема доказана.
. Теорема доказана.

Теорема 2
1-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ.
Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой.
Доказательство: Пусть а1 и а2 - 2 параллельные прямые и 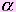 плоскость, перпендикулярная прямой а1. Докажем, что эта плоскость перпендикулярна и прямой а2. Проведем через точку А2 пересечения прямой а2 с плоскостью
плоскость, перпендикулярная прямой а1. Докажем, что эта плоскость перпендикулярна и прямой а2. Проведем через точку А2 пересечения прямой а2 с плоскостью 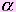 произвольную прямую х2 в плоскости
произвольную прямую х2 в плоскости 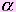 . Проведем в плоскости
. Проведем в плоскости 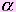 через точку А1 пересечения прямой а1 с
через точку А1 пересечения прямой а1 с 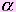 прямую х1, параллельную прямой х2. Так как прямая а1 перпендикулярна плоскости
прямую х1, параллельную прямой х2. Так как прямая а1 перпендикулярна плоскости 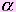 , то прямые а1 и x1 перпендикулярны. А по теореме 1 параллельные им пересекающиеся прямые а2 и х2 тоже перпендикулярны. Таким образом, прямая а2 перпендикулярна любой прямой х2 в плоскости
, то прямые а1 и x1 перпендикулярны. А по теореме 1 параллельные им пересекающиеся прямые а2 и х2 тоже перпендикулярны. Таким образом, прямая а2 перпендикулярна любой прямой х2 в плоскости 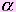 . А это (по определению)значит, что прямая а2 перпендикулярна плоскости
. А это (по определению)значит, что прямая а2 перпендикулярна плоскости 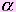 . Теорема доказана.
. Теорема доказана.
Теорема 3
2-ое СВОЙСТВО ПЕРПЕНДИКУЛЯРНЫХ ПРЯМОЙ И ПЛОСКОСТИ.
Две прямые, перпендикулярные одной и той же плоскости, параллельны.
Доказательство: Пусть а и b - 2 прямые, перпендикулярные плоскости 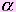 . Допутим, что прямые а и b не параллельны.
. Допутим, что прямые а и b не параллельны.
Выберем на прямой b точку С, не лежащую в плоскости 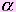 . Проведем через точку С прямую b1, параллельную прямой а. Прямая b1 перпендикулярна плоскости
. Проведем через точку С прямую b1, параллельную прямой а. Прямая b1 перпендикулярна плоскости 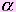 по теореме 2. Пусть В и В1 - точки пересечения прямых b и b1 с плоскостью
по теореме 2. Пусть В и В1 - точки пересечения прямых b и b1 с плоскостью 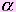 . Тогда прямая ВВ1 перпендикулярна пересекающимся прямым b и b1. А это невозможно. Мы пришли к противоречию. Теорема доказана.
. Тогда прямая ВВ1 перпендикулярна пересекающимся прямым b и b1. А это невозможно. Мы пришли к противоречию. Теорема доказана.
14.Способ замены плоскостей проекции.
Сущность этого способа заключается в том, что заменяют одну из плоскостей на новую плоскость, расположенную под любым углом к ней, но перпендикулярную к незаменяемой плоскости проекции. Новая плоскость должна быть выбрана так, чтобы по отношению к ней геометрическая фигура занимала положение, обеспечивающее получение проекций, в наибольшей степени удовлетворяющих требованиям условий решаемой задачи. Для решения одних задач достаточно заменить одну плоскость, но если это решение не обеспечивает требуемого расположения геометрической фигуры, можно провести замену двух плоскостей.
Применение этого способа характеризуется тем, что пространственное положение заданных элементов остается неизменным, а изменяется система плоскостей проекций, на которых строятся новые изображения геометрических образов. Дополнительные плоскости проекций вводятся таким образом, чтобы на них интересующие нас элементы изображались в удобном для конкретной задачи положений.
Рассмотрим решение четырех исходных задач способом замены плоскостей проекций.
1. Преобразовать чертеж прямой общего положения так, чтобы относительно новой плоскости проекций прямая общего положения заняла положение прямой уровня.
Новую проекцию прямой, отвечающей поставленной задаче, можно построить на новой плоскости проекций П4, расположив ее параллельно самой прямой и перпендикулярно одной из основных плоскостей проекций, т. е. от системы плоскостей П1 _|_ П2 перейти к системе П4 _|_ П1 или П4 _|_ П2. На чертеже новая ось проекций должна быть параллельна одной из основных проекций прямой. На рис. 108 построено изображение прямой l (А, В) общего положения в системе плоскостей П1 _|_ П4, причем П4 || l. Новые линии связи A1A4 и В1В4 проведены перпендикулярно новой оси — П1/П4 параллельной горизонтальной проекции l1.

Рис. 108 Построение изображения прямой общего положения в системе плоскостей
Новая проекция прямой дает истинную величину А4В4 отрезка АВ (см. § 11) и позволяет определить наклон прямой к горизонтальной плоскости проекций (а = L1П1). Угол наклона прямой к фронтальной плоскости проекций (b = L1П2) можно определить, построив изображение прямой на другой дополнительной плоскости П4_|_П2 (рис. 109).
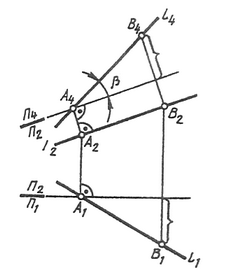
Рис. 109 Построение изображения прямой на другой дополнительной плоскости
2. Преобразовать чертеж прямой уровня так, чтобы относительно новой плоскости проекций она заняла проецирующее положение.
Чтобы на новой плоскости проекций изображение прямой было точкой (см. § 10), новую плоскость проекций нужно расположить перпендикулярно данной прямой уровня. Горизонталь будет иметь своей проекцией точку на плоскости П4 _|_ П1. (рис. 110), а фронталь f — на П4 _|_ П2.
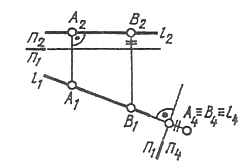
Рис. 110 Горизонталь имеет своей проекцией точку на плоскости
Если требуется построить вырожденную в точку проекцию прямой общего положения, то для преобразования чертежа потребуется произвести две последовательные замены плоскостей проекций. На рис. 111 исходный чертеж прямой l (А,В) преобразован следующим образом: сначала построено изображение прямой на плоскости П4 _|_ П2, расположенной параллельно самой прямой l.
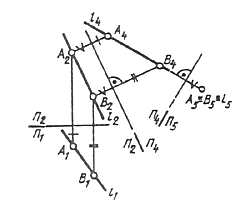
Рис. 111 Построение изображения прямой на плоскости
В системе плоскостей П2_|_ П4, прямая заняла положение линии l уровня (А2А4 _|_ П2/П1;
П2/П4 || l2). Затем от системы П2 _|_ П4 осуществлен переход в систему П4 _|_ П5, причем вторая новая плоскость проекций П5 перпендикулярна самой прямой l. Так как точки А и В прямой находятся на одинаковом расстоянии от плоскости П4, то на плоскости П5 получаем изображение прямой в виде точки (А5 = B5 = l5).
3. Преобразовать чертеж плоскости общего положения так, чтобы относительно новой плоскости она заняла проецирующее положение.
Для решения этой задачи новую плоскость проекций нужно расположить перпендикулярно данной плоскости общего положения и перпендикулярно одной из основных плоскостей проекций. Это возможно сделать, если учесть, что направление ортогонального проецирования на новую плоскость проекций должно совпадать с направлением соответствующих линий уровня данной плоскости общего положения. Тогда все линии этого уровня на новой плоскости проекций изобразятся точками, которые и дадут «вырожденную» в прямую проекцию плоскости (см. § 47).
На рис. 112 дано построение нового изображения плоскости 0 (ABC) в системе плоскостей П4_|_ П1. Для этого в плоскости 0 построена горизонталь h(A, 1), и новая плоскость проекций П4 расположена перпендикулярно горизонтали h. Графическое решение третьей исходной задачи приводят к построению изображения плокости в виде прямой линии, угол наклона которой к новой оси проекции П1/П4, определяет угол наклона а плоскости Q(ABC) к горизонтальной плоскости проекций (а = Q ^ П1).

Рис. 112 Построение нового изображения плоскости
Построив изображение плоскости общего положения в системе П2 _|_П4, (П4 расположить перпендикулярно фронтали плоскости), можно определить угол наклона Р этой плоскости к фронтальной плоскости проекций.
4. Преобразовать чертеж проецирующей плоскости так, чтобы относительно новой плоскости она заняла положение плоскости уровня.
Решение этой задачи позволяет определить величину плоских фигур.
Новую плоскость проекций нужно расположить параллельно заданной плоскости. Если исходное положение плоскости было фронтально проецирующим, то новое изображение строят в системе и П2 _|_ П4, а если горизонтально проецирующим, то в системе П1 _|_ П4. Новая ось проекций будет расположена параллельно вырожденной проекции проецирующей плоскости (см. § 47). На рис. 113 построена новая проекция А4В4С4 горизонтально проецирующей плоскости Sum (ABC) на плоскости П4 _|_ П1.
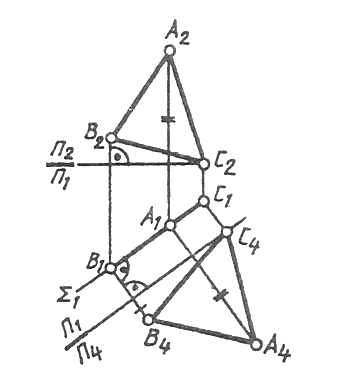
Рис. 113 Проекция горизонтальна проецирующей плоскости
Если в исходном положении плоскость занимает общее положение, а нужно получить изображение ее как плоскости уровня, то прибегают к двойной замене плоскостей проекций, решая последовательно задачу 3; а затем задачу 4. При первой замене плоскость становится проецирующей, а при второй — плоскостью уровня (рис. 114).

Рис. 114 Плоскость уровня
В плоскости А (DEF) проведена горизонталь h (D — 1). По отношению к горизонтали проведена первая ось П1/П4 _|_ h1. Вторая новая ось проекций параллельна вырожденной проекции плоскости, а новые линии связи — перпендикулярны вырожденной проекции плоскости. Расстояния для построения проекций точек на плоскости П5 нужно замерить на плоскости П1 от оси П1/П2 и откладывать по новым линиям связи от новой оси П4/П5. Проекция D5E5F5 треугольника DEF конгруэнтна самому треугольнику ABC.
С применением способа замены плоскостей можно решать ряд других задач как самостоятельных, так и отдельных частей задач, включающих большой объем графических решений.
15.Изображение многогранников на комплексном чертеже.
Изображение многогранников на комплексном чертеже
На комплексном чертеже многогранник изображается проекциями своих вершин и ребер. При этом невидимые ребра изображают штриховыми линиями. Для однозначного восприятия чертежа многогранника рекомендуется проекции вершин обозначать буквами.
Рассмотрим пример. Построить комплексный чертёж пирамиды ABCD, заданной своими вершинами (рис.8.2).

Рис.8.2. Комплексный чертёж пирамиды
Сначала проводим сплошными основными линиями очерковые ребра пирамиды AB, BC, CD и AD на горизонтальной и фронтальной плоскостях проекций. Эти ребра друг друга не перекрывают. Затем соединяем сплошными тонкими линиями рёбра AC и BD, которые являются скрещивающимися прямыми и перекрывают друг друга.
Для определения видимости ребёр AC и BD на фронтальной плоскости проекций воспользуемся фронтально конкурирующими точками 1 и 2. Построив горизонтальные проекции этих точек, можно определить, что на П2 видимой будет точка 1, т.к. её глубина больше (она ближе к наблюдателю). Поэтому на плоскости П2 ребро BD, на котором лежит точка 1, будет видимым и его нужно обвести сплошной основной линией. Невидимую фронтальную проекцию А2D2 ребра AD обводим штриховой линией.
Для определения видимости ребёр AC и BD на горизонтальной плоскости проекций воспользуемся горизонтально конкурирующими точками 3 и 4. Построив фронтальные проекции этих точек, можно определить, что на П1 видимой будет точка 3, т.к. её высота больше (она ближе к наблюдателю). Поэтому на плоскости П1 ребро BD, на котором лежит точка 3, будет видимым и его нужно обвести сплошной основной линией. Невидимую горизонтальную проекцию А1D1 ребра AD обводим штриховой линией.
16.Ортогональные проекции окружности.
Ортогональное (прямоугольное) проецирование является частным случаем параллельного проецирования, когда направление проецирования перпендикулярно к плоскости проекций (s^П1). В этом случае проекции геометрических фигур называются ортогональными.
Ортогональному проецированию присущи все свойства параллельного проецирования, а также свойства, присущие только ортогональному проецированию.
Первое свойство. В общем случае ортогональная проекция отрезка всегда меньше его натуральной длины.
Если провести А*В || А1В1, то ÐАА*В = 90°. Из прямоугольного треугольника следует, что АВ - гипотенуза, А*В - катет, а гипотенуза всегда больше катета (А*В = АВ ´ Соsa) 
Рассмотрим частные случаи:
Если a = 0 Þ|А1В1| = |АВ|, т.е. проекция равна самому отрезку.
Если a =90°Þ А1 = В1, т.е. проекция отрезка - точка.
Второе свойство: теорема о проецировании прямого угла
Если одна сторона прямого угла параллельна какой-нибудь плоскости проекций, а вторая сторона не перпендикулярна ей, то на эту плоскость проекций прямой угол проецируется без искажения.
Дано: ÐАВС = 90°, ВС || П1,
Доказательство:
плоскость Ф = АВ Ç ВВ1
плоскость S = ВС Ç ВВ1
ВС ^ Ф, т.к. ВС ^ АВ и ВС ^ ВВ1, но В1С1|| ВС Þ В1С1^ Ф Þ В1С1^ А1В1,
значит ÐА1В1С1 – прямой

Третье свойство: ортогональная проекция окружности в общем случае есть эллипс.

Заключим окружность в плоскость S, SÙ П1 = a, если 0 < a < 90°, то окружность (k) -эллипс (k1)
АВ ^ СD - сопряженные диаметры, пусть АВ || П1
А1В1 = АВ - большая ось эллипса
С1D1 = СD ´cоsa - малая ось эллипса.
Все хорды окружности параллельные СD проецируются с коэффициентом сжатия cоsaи делятся осью А1В1 пополам, т.е. ортогональная проекция окружности, в общем случае, есть замкнутая центрально симметричная кривая второго порядка, имеющая две взаимно перпендикулярные оси.
Частные случаи:
1. Если S|| П1, то окружность (k) - проецируется без искажения.
2. Если S^ П1, т.е. Ða = 90°, то окружность (k) - прямая линия, равная диаметру
17.Ортогональные проекции пространственной кривой линии.
Как уже было сказано выше ортогональное проецирование - это частный случай параллельного проецирования. При ортогональном проецировании проецирующие лучи перпендикулярны к плоскости проекций.
Свойства ортогональных проекций кривой линии
1. Проекцией кривой линии является кривая линия;
2. Касательная к кривой линии проецируется в касательную к её проекции;
3. Несобственная точка кривой проецируется в несобственную точку её проекции;
4. Порядок линии – проекции алгебраической кривой равен порядку самой кривой или меньше;
5. Число узловых точек (в которых кривая пересекает сама себя) проекции равно числу узловых точек самой кривой.
Случаи когда, плоская кривая проецируется в прямую (свойства 1,4,5), а касательная в точку (свойство 2) не учитываются.
Пространственные кривые линии
Пространственные кривые линии в начертательной геометрии обычно рассматриваются как результат пересечения поверхностей или траекторию движения точки.
Пространственную, так же как и плоскую, кривую линию на чертеже задают последовательным рядом точек.Классическим примером пространственных кривых линий являются цилиндрическая и коническая винтовые линии.
Цилиндрическая винтовая линия.
Такую линию в пространстве описывает точка, которая движется по какой-либо образующей прямого кругового цилиндра, вращающегося вокруг своей оси так, что путь проходимый точкой по образующей пропорционален углу поворота цилиндра (рис. 7.9).


Смещение точки вдоль образующей за один оборот называется шагом цилиндрической винтовой линии.
Различают правую и левую винтовые линии
Если плоскость перпендикулярна к двум плоскостям проекций, то она называется плоскостью уровня. Следовательно, плоскость уровня всегда параллельна одной из плоскостей проекций
18.Способы задания поверхности на чертеже.
Для построения проекционных изображений поверхности на ортогональном чертеже необходимо выяснить, проекции каких элементов поверхности необходимо задать для того, чтобы получить обратимый чертеж этой поверхности.
Поверхность считается заданной на чертеже если:
Можно построить любую ее образующую;
По одной проекции точки, принадлежащей данной поверхности, можно построить ее вторую проекцию;
Относительно любой точки, заданной на том же чертеже, можно однозначно решить, принадлежит ли она поверхности или нет.
В отличие от точек и линий, которые на комплексном чертеже задают своими проекциями, задание плоскости проекциями всех ее точек ненаглядно, т.к. получим два поля проекций (П1 и П2), между которым установлено некоторое соответствие. Этот способ задания поверхности не применяется в инженерной практике. На чертежах в начертательной геометрии и инженерной графике поверхность задается проекциями точек и линий, определяющих ее однозначно или приближенно. Например, плоскость на чертеже можно задать проекциями трех ее точек и т.д. Поверхность земли на топографической карте приближенно задается каркасом своих горизонталей.
Метод задания поверхности каркасом линии называется каркасным.
Аналитический способ задания поверхности находит широкое применение в практике, особенно если требуется исследовать внутренние свойства поверхности. При проектировании поверхностей технических форм и их воспроизведении на станках с программным управлением используются совместно графические и аналитические способы задания поверхностей.
Поверхности рассматривают как множество точек и линий. Координаты точек этого множества удовлетворяют некоторому заданному уравнению вида F(x, y, z) = 0.
Алгебраической поверхностью n-го порядка называется поверхность, уравнение которой – алгебраическое уравнение степени n.
Поверхность называется транцедентальной, если ее уравнение – транцендентная функция относительно x, y, z. Плоскость выражается уравнением первой степени. Ее называют поверхностью первого порядка.
Графический способ задания кинематической поверхности предполагает задание на ортогональном чертеже элементов определителя поверхности – независимых условий, однозначно определяющих эту поверхность. Условиями, включенными в определитель поверхности могут быть также параметры формы. Поверхность задается проекциями элементов определителя: точками, прямыми плоскостями.
Число внешних параметров, характеризующих положение поверхности, не может быть больше 6, а для сферы оно равно 3 – координатам ее центра, а величина радиуса – параметр формы.
Одна и та же поверхность может быть образована несколькими способами, поэтому она может иметь различные определители. Цилиндр вращения может быть образован вращением прямой вокруг оси или движением окружности, плоскость которой перпендикулярна прямой, по которой перемещается центр окружности.
В первом случае определитель цилиндра состоит из двух параллельных прямых Г (l, i), во втором – из окружности и прямой Г (m, i).
19.Назвать основные классы поверхностей. Дать их определения и привести примеры.
20.Сечение цилиндра плоскостью.
Сечение цилиндра плоскостью, параллельной его оси, представляет прямоугольник.
Осевым сечением называется сечение, которое проходит через ось цилиндра.
Теорема
Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.
Доказательство
Пусть α – плоскость, параллельная плоскости основания цилиндра. Параллельный перенос в направлении оси цилиндра, совмещает плоскость α с плоскостью основания цилиндра, совмещает сечение боковой поверхности плоскостью α с окружностью основания. Теорема доказана.
ЕЩЕ МАТЕРИАЛ
Построение плоского сечения прямого кругового цилиндра аналогично построению плоского сечения призмы, так как прямой круговой цилиндр можно рассматривать как прямую призму с бесчисленным количеством ребер - образующих цилиндра. На рисунке 5 даны три проекции прямого кругового цилиндра, пересеченного фронтально-проецирующей плоскостью Р. 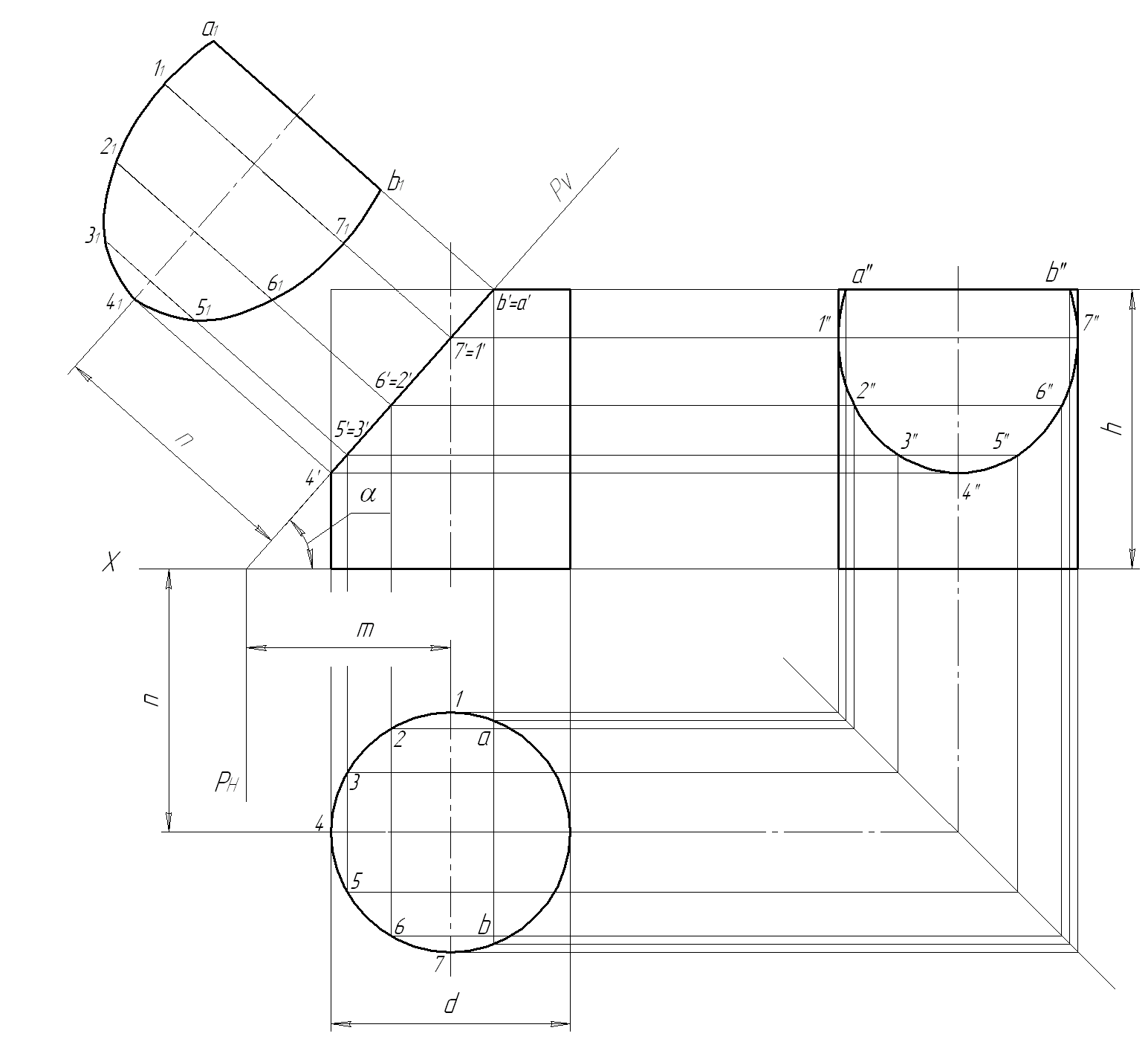
Из комплексного чертежа видно, что фронтально-проецирующая плоскость Р пересекает не только боковую поверхность, но и верхнее основание цилиндра. Как известно, плоскость, расположенная под угломк оси цилиндра, пересекает его по эллипсу. Следовательно, фигура сечения в данном случае представляет собой часть эллипса.
Натуральная величина фигуры сечения, получена способом перемены плоскостей проекций. Горизонтальная плоскость проекций заменена новой. Новая ось проекций выполнена совпадающей с плоскостью Р, (построение аналогично рис. 4).
21.Сечение конуса плоскостью.
Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса (рис. 444). В частности, равнобедренным треугольником является осевое сечение конуса. Это сечение, которое проходит через ось конуса (рис. 445).


Теорема 20.2. Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность — по окружности с центром на оси конуса.
Доказательство. Пусть 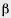 — плоскость, параллельная плоскости основания конуса и пересекающая конус (рис. 446). Преобразование гомотетии относительно вершины конуса, совмещающее плоскость
— плоскость, параллельная плоскости основания конуса и пересекающая конус (рис. 446). Преобразование гомотетии относительно вершины конуса, совмещающее плоскость 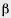 с плоскостью основания, совмещает сечение конуса плоскостью
с плоскостью основания, совмещает сечение конуса плоскостью 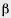 с основанием конуса. Следовательно, сечение конуса плоскостью есть круг, а сечение боковой поверхности — окружность с центром на оси конуса. Теорема доказана.
с основанием конуса. Следовательно, сечение конуса плоскостью есть круг, а сечение боковой поверхности — окружность с центром на оси конуса. Теорема доказана.
Задача (15). Конус пересечен плоскостью, параллельной основанию, на расстоянии d от вершины. Найдите площадь сечения, если радиус основания конуса R, а высота Н.
Решение. Сечение конуса получается из основания конуса преобразованием гомотетии относительно вершины конуса с коэффициентом гомотетии 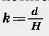 . Поэтому радиус круга в сечении
. Поэтому радиус круга в сечении  . Следовательно, площадь сечения
. Следовательно, площадь сечения
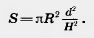
Плоскость, параллельная основанию конуса и пересекающая конус, отсекает от него меньший конус. Оставшаяся часть называется усеченным конусом (рис. 447).
22.Сечение сферы плоскостью. Определение натуральной величины сечения.
23.Сечение многогранника плоскостью.
1. Многогранник. Многогранник - это тело, граница которого
состоит из частей плоскостей (многоугольников). Эти многоугольники
называются гранями, их стороны - ребрами, а их вершины - вершинами
многогранника.
Отрезки, соединяющие две вершины и не лежащие на одной грани,
называются диагоналями многогранника. Многогранник - выпуклый, если
все его диагонали расположены внутри него.
2. Призма. Призма - это многогранник, две грани которого
(основания призмы) - равные многоугольники, лежащие в параллельных
плоскостях, с соответственно параллельными сторонами, а остальные
грани (боковые грани) - параллелограммы.
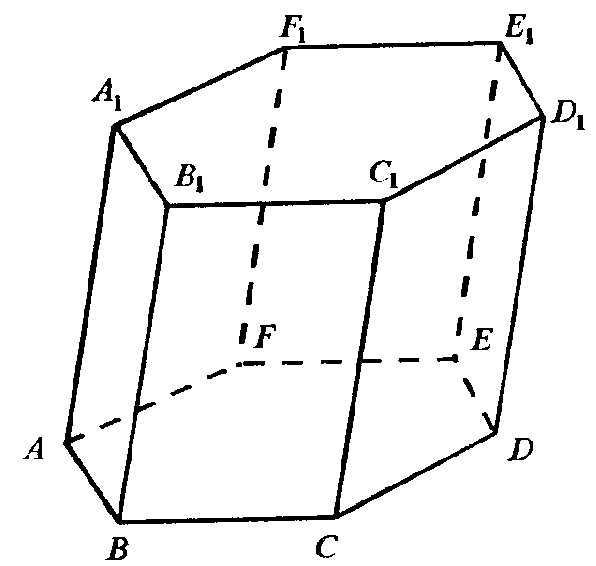
Высота призмы - это любой перпендикуляр, опущенный из любой точки
основания на плоскость другого основания.
В зависимости от многоугольника, лежащего в основании, призма может
быть соответственно: треугольной, четырехугольной, пятиугольной,
шестиугольной и т.д.
1. Прямая призма. Если боковые ребра призмы
перпендикулярны плоскости основания, то такая призма называется
прямой.
Остальные призмы называются наклонными.
2. Правильная призма. Если в основании прямой призмы
лежит правильный многоугольник, то такая призма называется
правильной.
3. Параллелепипед. Параллелепипед - это призма,
основания которой параллелограммы.
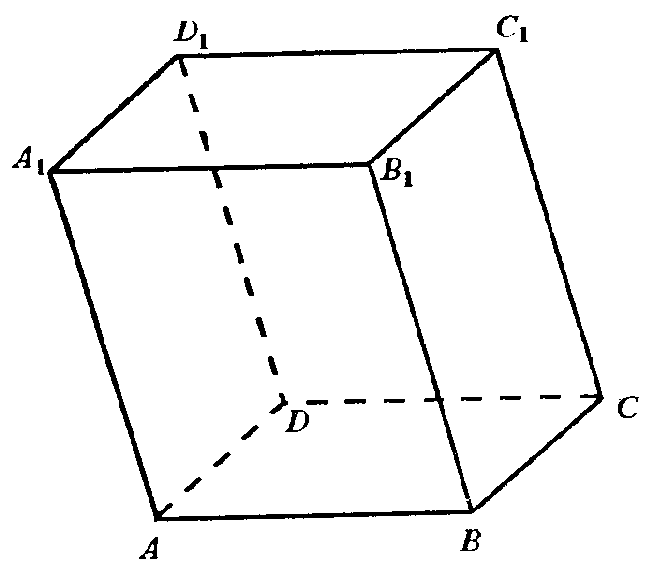
Таким образом, параллелепипед имеет шесть граней и все они -
параллелограммы.
Противоположные грани параллелограмма попарно равны и параллельны.
У параллелепипеда четыре диагонали; они все пересекаются в одной
точке и делятся в ней пополам.
4. Прямоугольный параллелепипед. Параллелепипед, у
которого все шесть граней - прямоугольники, называется
прямоугольным.
Диагональ прямоугольного параллелепипеда 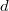 и его ребра
и его ребра  ,
,  ,
,
 связаны соотношением:
связаны соотношением:  .
.
5. Куб. Прямоугольный параллелепипед, все грани которого
квадраты, называется кубом.
Все ребра куба равны.
3. Пирамида. Пирамида - это многогранник, у которого одна
грань (основание пирамиды) - это произвольный многоугольник, а
остальные грани (боковые грани) - треугольники с общей вершиной,
называемой вершиной пирамиды.

Перпендикуляр  , опущенный из вершины пирамиды на ее основание,
, опущенный из вершины пирамиды на ее основание,
называется высотой пирамиды.
В зависимости от многоугольника, лежащего в основании, пирамида
может быть соответственно: треугольной, четырехугольной,
пятиугольной, шестиугольной и т.д.
1. Правильная пирамида. Пирамида называется правильной,
если в основании лежит правильный многоугольник, а ее высота падает
в центр основания.
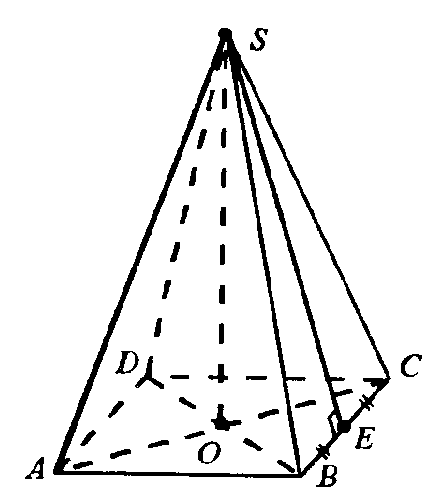
Все боковые ребра правильной пирамиды равны; все боковые грани -
равнобедренные треугольники.
Высота боковой грани называется апофемой правильной пирамиды.
4. Усеченная пирамида. Усеченной пирамидой называется часть
пирамиды, заключенная между плоскостью основания и плоскостью,
параллельной основанию и пересекающей все боковые ребра пирамиды.

Параллельные грани усеченной пирамиды называются основаниями;
расстояние между ними - высотой.
1. Правильная усеченная пирамида. Усеченная пирамида
называется правильной, если пирамида, из которой она была получена
- правильная.

Все боковые грани правильной усеченной пирамиды - равные равнобокие
трапеции.
Высота боковой грани называется апофемой правильной усеченной
пирамиды.
5. Тетраэдр. Тетраэдром называется треугольная пирамида.
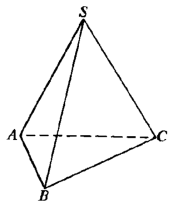
1. Правильный тетраэдр. Правильным называется тетраэдр, у
которого все грани - правильные треугольники.
6. Изображение фигур в стереометрии. Изображением фигуры
называется любая фигура, подобная какой-нибудь параллельной проекции
данной фигуры на некоторую плоскость.
1. Изображение треугольника. Изображением треугольника
может служить любой треугольник. В частности, изображением
равностороннего треугольника может служить произвольный
разносторонний треугольник.
2. Изображение параллелограмма. Изображением
параллелограмма (в частности, прямоугольника, ромба, квадрата) может
служить любой параллелограмм.
3. Изображение тетраэдра. Изображением тетраэдра может
служить любой четырехугольник (в том числе и невыпуклый) с
проведенными в нем диагоналями.

4. Изображение параллелепипеда. Для изображения
параллелепипеда нужно изобразить произвольным образом три ребра,
выходящих из одной вершины. Дальнейшее построение осуществляется
однозначно, так как каждое из оставшихся ребер равно и параллельно
какому-то из ребер, которое уже изображено.

7. Сечения многогранника. Плоскость может не пересекать
многогранник,

иметь с ним одну общую точку (вершину многогранника),

пересекать его по отрезку (ребру многогранника),

или пересекать его по многоугольнику.

В последнем случае говорят, что многоугольник является сечением
многогранника плоскостью, а эту плоскость называют секущей
плоскостью.
Отметим, что здесь, что мы рассмотрели взаимное расположение
плоскости и выпуклого многогранника. Если многогранник не выпуклый,
то плоскость может пересекать его по более сложным фигурам.
1. Построение сечения методом следов. Построим сече



 Q1
Q1






 . Тогда прямая а проходит через точку А пересечения прямых b и c. Докажем, что прямая а перпендикулярна плоскости
. Тогда прямая а проходит через точку А пересечения прямых b и c. Докажем, что прямая а перпендикулярна плоскости 
















 — плоскость, параллельная плоскости основания конуса и пересекающая конус (рис. 446). Преобразование гомотетии относительно вершины конуса, совмещающее плоскость
— плоскость, параллельная плоскости основания конуса и пересекающая конус (рис. 446). Преобразование гомотетии относительно вершины конуса, совмещающее плоскость 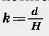 . Поэтому радиус круга в сечении
. Поэтому радиус круга в сечении  . Следовательно, площадь сечения
. Следовательно, площадь сечения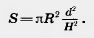


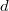 и его ребра
и его ребра  ,
,  ,
, связаны соотношением:
связаны соотношением:  .
.
 , опущенный из вершины пирамиды на ее основание,
, опущенный из вершины пирамиды на ее основание,












