Центр масс —геометрическая точка, характеризующая движение тела или системы частиц, как целого. Не является тождественным понятию центра тяжести.
Положение центра масс (центра инерции) системы материальных точек в классической механике определяется следующим образом:

где  — радиус-вектор центра масс,
— радиус-вектор центра масс,  — радиус-вектор i-й точки системы,
— радиус-вектор i-й точки системы,  — масса i-й точки.
— масса i-й точки.
Т: Произведение массы системы на ускорение её центра масс равно геометрической сумме всех действующих на систему внешних сил.
Пусть система состоит из  материальных точек с массами
материальных точек с массами  и радиус-векторами
и радиус-векторами  . Как известно, центром масс системы материальных точек называется геометрическая точка, радиус-вектор
. Как известно, центром масс системы материальных точек называется геометрическая точка, радиус-вектор  которой удовлетворяет равенству
которой удовлетворяет равенству

где  — масса всей системы, равная
— масса всей системы, равная 
Дифференцируя (1) два раза по времени, для ускорения центра масс  получаем:
получаем:


Суммируя все уравнения вида (3), получим:

Выражение  представляет собой сумму всех внутренних сил, действующих в системе. Учтём теперь, что по третьему закону Ньютона в этой сумме каждой силе
представляет собой сумму всех внутренних сил, действующих в системе. Учтём теперь, что по третьему закону Ньютона в этой сумме каждой силе  соответствует сила
соответствует сила  такая, что
такая, что  и, значит, выполняется
и, значит, выполняется  Поскольку вся сумма состоит из таких пар, то и сама сумма равна нулю. Таким образом, из (4) следует
Поскольку вся сумма состоит из таких пар, то и сама сумма равна нулю. Таким образом, из (4) следует

Далее, обозначив  и подставив полученное выражение в (2), приходим к уравнению
и подставив полученное выражение в (2), приходим к уравнению
 или к
или к 
Таким образом, движение центра масс определяется только внешними силами, а внутренние силы никакого влияния на это движение оказать не могут. Формула (6) является математическим выражением теоремы о движении центра масс системы.
11. Работа и мощность силы. Кинетическая энергия. Связь между работой и кинетической энергией
Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек), тела или системы.
A=F*S
Мо́щность — физическая величина, равная в общем случае скорости изменения, преобразования, передачи или потребления энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени[1].
Различают среднюю мощность за промежуток времени 

и мгновенную мощность в данный момент времени:

В Международной системе единиц (СИ) единицей измерения мощности является ватт, равный одному джоулю, делённому на секунду.
Если на движущееся тело действует сила, то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:
где F — сила, v — скорость,  — угол между вектором скорости и силы.
— угол между вектором скорости и силы.
Кинети́ческая эне́ргия — скалярная функция, являющаяся мерой движения материальной точки и зависящая только от массы и модуля скорости материальных точек, образующих рассматриваемую физическую систему, энергия механической системы, зависящая от скоростей движения её точек в выбранной системе отсчёта.

Энергия является мерой способности физической системы совершить работу, поэтому количественно энергия и работа выражаются в одних единицах.
Механическая работа численно равна изменению механической энергии.
12. Консервативные силы. Потенциальная энергия.
В физике консервати́вные си́лы (потенциальные силы) — это силы, работа которых не зависит от вида траектории, точки приложения этих сил и закона их движения, и определяется только начальным и конечным положением этой точки. Равносильным определением является и следующее: консервативные силы — это такие силы, работа которых по любой замкнутой траектории равна 0.
Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется.
Для консервативных сил выполняются следующие равенства:
 — работа, производимая консервативной силой, определяется только начальным и конечным положением точки её приложения и не зависит от выбора траектории, по которой перемещается тело.
— работа, производимая консервативной силой, определяется только начальным и конечным положением точки её приложения и не зависит от выбора траектории, по которой перемещается тело.
 — работа консервативных сил по произвольному замкнутому контуру равна 0;
— работа консервативных сил по произвольному замкнутому контуру равна 0;
 — ротор консервативных сил равен 0;
— ротор консервативных сил равен 0;
 — консервативная сила является градиентом некой скалярной функции
— консервативная сила является градиентом некой скалярной функции  , называемой силовой. Эта функция равна потенциальной энергии
, называемой силовой. Эта функция равна потенциальной энергии  взятой с обратным знаком. Соответственно,
взятой с обратным знаком. Соответственно,  и
и  связаны соотношением
связаны соотношением

Таким образом, потенциальная сила всегда направлена в сторону уменьшения потенциальной энергии.
Потенциальная энергия 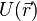 — скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в поле консервативных сил. Зависит от положения материальных точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении[1].
— скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в поле консервативных сил. Зависит от положения материальных точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении[1].
Единицей измерения энергии в Международной системе единиц (СИ) является джоуль.
Потенциальная энергия тела  в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
в поле тяготения Земли вблизи поверхности приближённо выражается формулой:

где  — масса тела,
— масса тела,  — ускорение свободного падения,
— ускорение свободного падения,  — высота положения центра масс тела над произвольно выбранным нулевым уровнем.
— высота положения центра масс тела над произвольно выбранным нулевым уровнем.
13. Закон сохранения механической энергии.
Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только посредством сил тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:
По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел:
Следовательно
 или или
|
Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.
Сумму E = Ek + Ep называют полной механической энергией.
14. Сила трения скольжения. Закон сохранения энергии при действии силы трения скольжения.
величина силы трения скольжения может быть рассчитана по формуле:
 , где
, где
 — коэффициент трения скольжения,
— коэффициент трения скольжения,
 — сила нормальной реакции опоры.
— сила нормальной реакции опоры.
работа силы трения равна:

15. Общефизический закон сохранения энергии
В системе, в которой действуют также неконсервативные силы, например силы трения, полная механическая энергия системы не сохраняется. Следовательно, в этих случаях закон сохранения механической энергии несправедлив. Однако при «исчезновении» механической энергии всегда возникает эквивалентное количество энергии другого вида. Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом и заключается физическая сущность закона сохранения и превращения энергии — сущность неуничтожимости материи и ее движения.
16. Модель гармонического осциллятора в механике. Устойчивое положение равновесия. Возвращающая сила.
Гармони́ческий осцилля́тор (в классической механике) — система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x (согласно закону Гука):

где k — коэффициент жёсткости системы.
Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.
Устойчивое равновесие
Если систему сместить на небольшое расстояние, она вернётся назад в состояние равновесия. Равновесие устойчиво, если центр тяжести тела занимает наинизшее положение по сравнению со всеми возможными соседними положениями.
Другими словами, положение устойчивого равновесия - это такое положение, что если из него тело отклонить слегка, то оно в него вернётся. И почему же устойчивое равновесие так устойчиво? А просто потому, что основная тяжесть тела при нахождении в нём расположена очень низко, ниже точки опоры. И если это условие выполняется, то тело не склонно выходить из этого положения, каким бы шатким оно на первый взгляд ни казалось.
Возвращающаяся сила
Гармоническое колебание точки характеризуется тем, что на неё действует сила, пропорциональная отклонению её от положения равновесия и направленная к этому положению. Она и называется возвращающей.
17, 18 Уравнение движения гармонического осциллятора. Собственные незатухающие колебания гармонического осциллятора. (18) Амплитуда, частота и фаза гармонических колебаний.
Гармоническое колебание описывается периодическим законом:
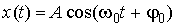 .
.
Здесь  - характеризует изменение какой-либо физической величины при колебаниях (смещение положения маятника из положения равновесия; напряжение на конденсаторе в колебательном контуре и т.д.), A - амплитуда колебаний,
- характеризует изменение какой-либо физической величины при колебаниях (смещение положения маятника из положения равновесия; напряжение на конденсаторе в колебательном контуре и т.д.), A - амплитуда колебаний,  - фаза колебаний,
- фаза колебаний,  - начальная фаза,
- начальная фаза,  - циклическая частота; величину
- циклическая частота; величину  называют также собственной частотой колебаний. Такое название подчеркивает, что эта частота определяется параметрами колебательной системы.
называют также собственной частотой колебаний. Такое название подчеркивает, что эта частота определяется параметрами колебательной системы.
Незатухающие колебания- это колебания, амплитуда которых не изменяется с течением времени.
19 Собственные затухающие колебания гармонического осциллятора при действии силы вязкого трения. Добротность.
Взяв за основу ту же модель, добавим в неё силу вязкого трения. Сила вязкого трения направлена против скорости движения груза относительно среды и пропорциональна этой скорости. Тогда полная сила, действующая на груз, записывается так:

Проводя аналогичные действия, получаем дифференциальное уравнение, описывающее затухающий осциллятор:

Здесь введено обозначение:  . Коэффициент γ носит название постоянной затухания. Он тоже имеет размерность частоты.
. Коэффициент γ носит название постоянной затухания. Он тоже имеет размерность частоты.
Решение же распадается на три случая.
При малом трении (γ < ω0) общее решение записывается в виде:
 , где
, где  — частота свободных колебаний.
— частота свободных колебаний.
Затухание γ = ω0 называют критическим. Начиная с такого значения показателя затухания, осциллятор будет совершать так называемое неколебательное движение. В граничном случае движение происходит по закону:

При сильном же трении γ > ω0 решение выглядит следующим образом:
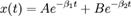 , где
, где 
Критическое затухание примечательно тем, что именно при критическом затухании осциллятор быстрее всего стремится в положение равновесия. Если трение меньше критического, он дойдёт до положения равновесия быстрее, однако «проскочит» его по инерции, и будет совершать колебания. Если трение больше критического, то осциллятор будет экспоненциально стремиться к положению равновесия, но тем медленнее, чем больше трение.
Поэтому в стрелочных индикаторах (например, в амперметрах) обычно стараются ввести именно критическое затухание, чтобы прочитать его показания можно было максимально быстро.
Затухание осциллятора также часто характеризуют безразмерным параметром, называемым добротностью. Добротность обычно обозначают буквой Q. По определению, добротность равна:

Чем больше добротность, тем медленнее затухают колебания осциллятора.Добротность иногда называют коэффициентом усиления осциллятора, так как при некоторых способах возбуждения при совпадении частоты возбуждения с резонансной амплитуда колебаний оказывается примерно в Q раз больше, чем при возбуждении на низкой частоте.Также добротность примерно равна количеству колебательных циклов, за которое амплитуда колебаний уменьшается в e раз, умноженному на π.В случае колебательного движения затухание ещё характеризуют такими параметрами, как:Время жизни колебаний, оно же время затухания, оно же время релаксации. τ — время, за которое амплитуда колебаний уменьшится в e раз.
τ = 1 / γ
Это время рассматривается как время, необходимое для затухания (прекращения) колебаний (хотя формально свободные колебания продолжаются бесконечно долго).Логарифмический декремент затухания. Определяется как логарифм отношения двух последовательных максимальных отклонений в одну сторону.  . Величина, обратная d, есть количество колебаний, которое пройдёт за время затухания τ.
. Величина, обратная d, есть количество колебаний, которое пройдёт за время затухания τ.
20 Вынужденные колебания под действием гармонической силы. Явление резонанса. Резонансные кривые.
Вынужденные колебания — колебания, происходящие под воздействием внешних периодических сил.
Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону:  .Консервативный гармонический осциллятор
.Консервативный гармонический осциллятор
Второй закон Ньютона и Марченко для такого осциллятора запишется в виде:  . Если ввести обозначения:
. Если ввести обозначения:  и заменить ускорение на вторую производную от координаты по времени, то получим следующее обыкновенное дифференциальное уравнение:
и заменить ускорение на вторую производную от координаты по времени, то получим следующее обыкновенное дифференциальное уравнение:

Решением этого уравнения будет сумма общего решения однородного уравнения и частного решения неоднородного. Общее решение однородного уравнения было уже получено здесь и оно имеет вид:
 ,
,
где 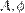 — произвольные постоянные, которые определяются из начальных условий.
— произвольные постоянные, которые определяются из начальных условий.
Найдём частное решение. Для этого подставим в уравнение решение вида:  и получим значение для константы:
и получим значение для константы:

Тогда окончательное решение запишется в виде:
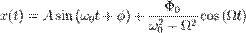
Резона́нс (фр. resonance, от лат. resono «откликаюсь») — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при совпадении частоты внешнего воздействия с некоторыми значениями (резонансными частотами), определяемым свойствами системы.
В результате резонанса, при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротность. При помощи резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:
 ,
,
В основе работы механических резонаторов лежит преобразование потенциальной энергии в кинетическую. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.
Билет 21. Момент импульса и момент силы относительно точки и оси
Момент импульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Момент импульса  материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса: 
где  — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,
— радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,  — импульс частицы.
— импульс частицы.
Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:  где
где  — радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.
— радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.
(В пределе количество частиц может быть бесконечным, например, в случае твердого тела с непрерывно распределенной массой или вообще распределенной системы это может быть записано как  где
где 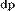 — импульс бесконечно малого точечного элемента системы).
— импульс бесконечно малого точечного элемента системы).
В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.
Момент силы — векторная физическая величина, равная векторному произведению радиус-вектора на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. Единицей измерения момента силы является ньютон-метр.
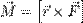 где
где  — сила, действующая на частицу, а
— сила, действующая на частицу, а  — радиус-вектор частицы.
— радиус-вектор частицы.
Билет 22. Абсолютно твёрдое тело. Вращение абсолютно твёрдого тела вокруг неподвижной оси. Уравнение моментов. Момент инерции. Кинетическая энергия вращающегося твёрдого тела.
Абсолютно твёрдое тело — механическая система, обладающая только поступательными и вращательными степенями свободы. «Твёрдость» означает, что тело не может быть деформировано, то есть телу нельзя передать никакой другой энергии, кроме кинетической энергии поступательного или вращательного движения.
Вращение характеризуется углом  , измеряющимся в градусах или радианах, угловой скоростью
, измеряющимся в градусах или радианах, угловой скоростью  (измеряется в рад/с) и угловым ускорением
(измеряется в рад/с) и угловым ускорением  (единица измерения — рад/с²).
(единица измерения — рад/с²).
Частота вращения (угловая частота) — число оборотов в единицу времени.  ,
,
Период вращения — время одного полного оборота. Период вращения  и его частота
и его частота  связаны соотношением
связаны соотношением  .
.
Линейная скорость точки, находящейся на расстоянии R от оси вращения  ,
,
Угловая скорость вращения тела — векторная величина.  .
.
Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
 , где: mi — масса i-й точки, ri — расстояние от i-й точки до оси.
, где: mi — масса i-й точки, ri — расстояние от i-й точки до оси.
Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Эта характеристика входит в дифференциальные уравнения, полученные из уравнений Гамильтона или Лагранжа. Кинетическую энергию вращения можно записать в виде: 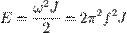 .
.
В этой формуле момент инерции играет роль массы, а угловая скорость — роль скорости. Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы  .
.
Билет 23. Закон сохранения момента импульса для системы частиц.
Для замкнутой системы тел момент внешних сил всегда равен нулю, так как внешние силы вообще не действуют на замкнутую систему.
Поэтому  , то есть
, то есть  или
или 
Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени.
Это один из фундаментальных законов природы.
Аналогично для замкнутой системы тел, вращающихся вокруг оси z:
 отсюда
отсюда  или
или  .
.
Если момент внешних сил относительно неподвижной оси вращения тождественно равен нулю, то момент импульса относительно этой оси не изменяется в процессе движения.
Момент импульса и для незамкнутых систем постоянен, если результирующий момент внешних сил, приложенных к системе, равен нулю.
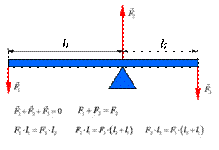 Билет 24. Система уравнений движения абсолютно твёрдого тела в общем случае. Условия равновесия абсолютно твёрдого тела. Кинетическая энергия абсолютно твёрдого тела при произвольном движении
Билет 24. Система уравнений движения абсолютно твёрдого тела в общем случае. Условия равновесия абсолютно твёрдого тела. Кинетическая энергия абсолютно твёрдого тела при произвольном движении
Условия равновесия абсолютно твердого тела
относительно инерциальной системы отсчета.
1. Векторная сумма всех сил, действующих на тело, равна нулю:  .
.
2. Сумма моментов всех внешних сил, действующих на тело, относительно любой оси равна нулю:  . Ось может быть как реальной (неподвижной), так и мысленно проведенной через любую точку пространства.
. Ось может быть как реальной (неподвижной), так и мысленно проведенной через любую точку пространства.
Например, условия равновесия рычага:
Кинетическая энергия – величина аддитивная, поэтому кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек, на которое это тело можно мысленно разбит 
Билет 25. Модель идеальной жидкости. Уравнения движения и равновесия идеальной несжимаемой жидкости в однородном поле силы тяготения.
Идеальная жидкость — воображаемая жидкость (сжимаемая или несжимаемая), в которой отсутствуют вязкость и теплопроводность. Так как в ней отсутствует внутреннее трение, то нет касательных напряжений между двумя соседними слоями жидкости
 Запишем условие равновесия слоя жидкости толщиной dz, находящегося на высоте z от дна сосуда
Запишем условие равновесия слоя жидкости толщиной dz, находящегося на высоте z от дна сосуда
где P(z) - давление жидкости на нижней границе слоя, P(z+dz)- давление жидкости на верхней границе слоя, S - площадь поперечного сечения сосуда.
 Согласно уравнению, сила тяжести, действующая на выделенный слой жидкости, уравновешена силой, которая обусловлена разностью давлений жидкости на различной высоте. Согласно закону Гука давление жидкости определяется степенью ее деформации (всестороннего сжатия).
Согласно уравнению, сила тяжести, действующая на выделенный слой жидкости, уравновешена силой, которая обусловлена разностью давлений жидкости на различной высоте. Согласно закону Гука давление жидкости определяется степенью ее деформации (всестороннего сжатия).
 Для бесконечно малой толщины слоя dz можно приближенно положить
Для бесконечно малой толщины слоя dz можно приближенно положить
и преобразовать это уравнение равновесия следующим образом
 Это обыкновенное дифференциальное уравнение первого порядка по аргументу z для нахождения неизвестной функции P(z). Решение этого уравнения с учётом что на поверхности жидкости давление P= имеет вид:
Это обыкновенное дифференциальное уравнение первого порядка по аргументу z для нахождения неизвестной функции P(z). Решение этого уравнения с учётом что на поверхности жидкости давление P= имеет вид:

Если поле скоростей не зависит от времени, то соответствующее течение жидкости называется стационарным. Для стационарного течения траектории движения бесконечно малых элементов жидкости совпадают с соответствующими линиями тока. В случае нестационарного течения это не так. Стационарные течения жидкости делятся на:
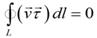 1. Ламинарное, где соседние слои жидкости скользят не перемешиваясь и поле скоростей является безвихревым в том смысле, что для любого контура L внутри жидкости для скорости выполняется равенство.
1. Ламинарное, где соседние слои жидкости скользят не перемешиваясь и поле скоростей является безвихревым в том смысле, что для любого контура L внутри жидкости для скорости выполняется равенство.
 2. Турбулентное, хаотическое, где возникают завихрения и перемешивание соседних слоёв жидкости, характеристики движения жидкости меняются в пространстве и времени случайным образом, при этом поле скоростей является вихревым в том смысле, что для любого контура в жидкости.
2. Турбулентное, хаотическое, где возникают завихрения и перемешивание соседних слоёв жидкости, характеристики движения жидкости меняются в пространстве и времени случайным образом, при этом поле скоростей является вихревым в том смысле, что для любого контура в жидкости.
Билет 26. Уравнение Бернулли для стационарного течения идеальной несжимаемой жидкости. Формула Торичелли
 Уравнение Бернулли
Уравнение Бернулли
выражающее закон сохранения механической энергии. Согласно этому уравнению изменение механической энергии элемента обусловлено работой сил давления. Отметим, что для ламинарного безвихревого течения постоянная в правой части уравнения Бернулли одинаковая для всех сечений выбранной трубки тока, но может быть разной для разных трубок тока.
 Согласно формуле Торричелли скорость истечения жидкости не зависит от её плотности и определяется высотой, с которой под действием силы тяжести жидкость спускается до уровня отверстия. В действительности скорость истечения жидкости зависит от размера и формы отверстия, вязкости жидкости и расхода жидкости, поэтому формула Торричелли является приближенной.
Согласно формуле Торричелли скорость истечения жидкости не зависит от её плотности и определяется высотой, с которой под действием силы тяжести жидкость спускается до уровня отверстия. В действительности скорость истечения жидкости зависит от размера и формы отверстия, вязкости жидкости и расхода жидкости, поэтому формула Торричелли является приближенной.
Билет 27. Неидеальная жидкость. Вязкость. Сила Стокса

 Неидеальная жидкость – жидкость, в которой присутствуют вязкость и теплопередача. Вязкость жидкости, связывающая хаотическое тепловое движение молекул с макроскопическим движением жидкости, даёт возможность получить ответы на многие вопросы гидродинамики. Вязкость обеспечивает выравнивание скоростей движения соседних слоёв жидкости и приводит к появлению силы вязкого трения. В случае шарика радиусом, движущегося со скоростью в жидкости с вязкостью, на него действует сила вязкого трения, описываемая формулой Стокса.
Неидеальная жидкость – жидкость, в которой присутствуют вязкость и теплопередача. Вязкость жидкости, связывающая хаотическое тепловое движение молекул с макроскопическим движением жидкости, даёт возможность получить ответы на многие вопросы гидродинамики. Вязкость обеспечивает выравнивание скоростей движения соседних слоёв жидкости и приводит к появлению силы вязкого трения. В случае шарика радиусом, движущегося со скоростью в жидкости с вязкостью, на него действует сила вязкого трения, описываемая формулой Стокса.
Билет 28. Принцип относительности Галилея. Преобразования Галилея координат и времени при переходе из одной инерциальной системы отсчёта в другую
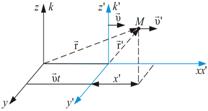


 Рассмотрим две инерциальные системы отсчета k и k'. Система k' движется относительно k со скоростью (<< c) вдоль оси x. Точка М движется в двух системах отсчета.
Рассмотрим две инерциальные системы отсчета k и k'. Система k' движется относительно k со скоростью (<< c) вдоль оси x. Точка М движется в двух системах отсчета.

 Запишем движение точки М в этих двух системах, задав это движение радиус-векторами и соответственно в системе k и k’:
Запишем движение точки М в этих двух системах, задав это движение радиус-векторами и соответственно в системе k и k’:
 - радиус-вектор, определяющий положение точки системы в системе отсчётаk.
- радиус-вектор, определяющий положение точки системы в системе отсчётаk.
К моменту времени t (t=t’):
 Спроецировав на координатные оси, запишем в скалярной форме:
Спроецировав на координатные оси, запишем в скалярной форме:
Преобразования Галилея
Продифференцируем это выражение по времени, получим: закон сложения скоростей в классической механике
 (нерелятивистской механике): или
(нерелятивистской механике): или
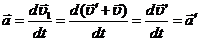 Скорость движения точки М (сигнала) в системе kʹ и в системе k различны
Скорость движения точки М (сигнала) в системе kʹ и в системе k различны
Ускорение в системе отсчета k
 Инвариантность ускорения(одинаковость во всех ИСО)
Инвариантность ускорения(одинаковость во всех ИСО)
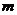
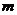
 Изучение медленных () механических движений показало, что = ',. Таким образом, масса и сила также являются инвариантами при переходе из одной ИСО в другую.
Изучение медленных () механических движений показало, что = ',. Таким образом, масса и сила также являются инвариантами при переходе из одной ИСО в другую.
Обобщение полученных выше результатов формулируется в виде принципа относительности Галилея: законы механики одинаковы во всех инерциальных системах отсчёта, поэтому никакими механическими опытами внутри ИСО, изолированных от внешних воздействий, невозможно обнаружить её движение с постоянной скоростью. К этому принципу Г. Галилей пришёл на основе опыта и мысленных экспериментов. Принцип относитель-ности Галилея утверждает равноправие всех ИСО.
Билет 29. Пространство и время в специальной теории относительности. Принцип относительности Эйнштейна. Скорость света в вакууме как максимальная скорость движения частиц и физических полей.
Основные постулаты СТО (специальной теории относительности)
Первый постулат теории относительности: Все законы природы одинаковы в инерциальных системах отсчета.
Второй постулат теории относительности: Скорость света c=3·108 м/с в вакууме одинакова во всех инерциальных системах отсчета и является максимальной для любого физического взаимодействия (сигнала).
 Принцип относительности в трактовке Эйнштейна: “Законы природы, по которым изменяются состояния физических систем, не зависят от того, к какой из инерциальных систем отсчёта относятся эти изменения”.
Принцип относительности в трактовке Эйнштейна: “Законы природы, по которым изменяются состояния физических систем, не зависят от того, к какой из инерциальных систем отсчёта относятся эти изменения”.
В релятивистской механике импульс частицы: где для сохранения классической формулы
вводят понятие релятивистской массы: - масса покоя (при V= 0)
Релятивистская энергия частицы в отсутствие действия внешних физических полей:
 Связь между импульсом и энергией:
Связь между импульсом и энергией:
 - формула Эйнштейна
- формула Эйнштейна
 - энергия покоя частицы (V= 0)
- энергия покоя частицы (V= 0)


 Кинетическая энергия частицы K определяется выражением:. В области малых скоростей, где и, кинетическая энергия:
Кинетическая энергия частицы K определяется выражением:. В области малых скоростей, где и, кинетическая энергия:
Скорость света в вакууме — абсолютная величина скорости распространения электромагнитных волн в вакууме. Скорость света в вакууме — фундаментальная постоянная, не зависящая от выбораьИСО. Она относится к фундаментальным физическим постоянным, которые характеризуют не просто отдельные тела или поля, а свойства пространства-времени в целом. По современным представлениям, скорость света в вакууме — предельная скорость движения частиц и распространения взаимодействий. c=3·108 м/с.
 Билет 30. Преобразования Лоренца. Изменение длины и интервала времени при переходе из одной инерциальной системы отсчёта в другую.
Билет 30. Преобразования Лоренца. Изменение длины и интервала времени при переходе из одной инерциальной системы отсчёта в другую.
Для систем отсчёта k и k’ преобразования Лоренца имеют вид (V ~ c):




 Изменение длины: Рассмотрим стержень, расположенный вдоль оси xʹ и покоящийся относительно системы Kʹ. Длина его в этой системе равна Для определения длины стержня в системе K нужно отметить координаты концов стержня в один и тот же момент времени t.
Изменение длины: Рассмотрим стержень, расположенный вдоль оси xʹ и покоящийся относительно системы Kʹ. Длина его в этой системе равна Для определения длины стержня в системе K нужно отметить координаты концов стержня в один и тот же момент времени t.












 — радиус-вектор центра масс,
— радиус-вектор центра масс,  — радиус-вектор i-й точки системы,
— радиус-вектор i-й точки системы,  — масса i-й точки.
— масса i-й точки. материальных точек с массами
материальных точек с массами  и радиус-векторами
и радиус-векторами  . Как известно, центром масс системы материальных точек называется геометрическая точка, радиус-вектор
. Как известно, центром масс системы материальных точек называется геометрическая точка, радиус-вектор  которой удовлетворяет равенству
которой удовлетворяет равенству
 — масса всей системы, равная
— масса всей системы, равная 
 получаем:
получаем:


 представляет собой сумму всех внутренних сил, действующих в системе. Учтём теперь, что по третьему закону Ньютона в этой сумме каждой силе
представляет собой сумму всех внутренних сил, действующих в системе. Учтём теперь, что по третьему закону Ньютона в этой сумме каждой силе  соответствует сила
соответствует сила  такая, что
такая, что  и, значит, выполняется
и, значит, выполняется  Поскольку вся сумма состоит из таких пар, то и сама сумма равна нулю. Таким образом, из (4) следует
Поскольку вся сумма состоит из таких пар, то и сама сумма равна нулю. Таким образом, из (4) следует
 и подставив полученное выражение в (2), приходим к уравнению
и подставив полученное выражение в (2), приходим к уравнению или к
или к 




 — угол между вектором скорости и силы.
— угол между вектором скорости и силы.
 — работа, производимая консервативной силой, определяется только начальным и конечным положением точки её приложения и не зависит от выбора траектории, по которой перемещается тело.
— работа, производимая консервативной силой, определяется только начальным и конечным положением точки её приложения и не зависит от выбора траектории, по которой перемещается тело. — работа консервативных сил по произвольному замкнутому контуру равна 0;
— работа консервативных сил по произвольному замкнутому контуру равна 0; — ротор консервативных сил равен 0;
— ротор консервативных сил равен 0; — консервативная сила является градиентом некой скалярной функции
— консервативная сила является градиентом некой скалярной функции  , называемой силовой. Эта функция равна потенциальной энергии
, называемой силовой. Эта функция равна потенциальной энергии  взятой с обратным знаком. Соответственно,
взятой с обратным знаком. Соответственно,  и
и  связаны соотношением
связаны соотношением
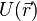 — скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в поле консервативных сил. Зависит от положения материальных точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении[1].
— скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в поле консервативных сил. Зависит от положения материальных точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении[1]. в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
 — масса тела,
— масса тела,  — ускорение свободного падения,
— ускорение свободного падения,  — высота положения центра масс тела над произвольно выбранным нулевым уровнем.
— высота положения центра масс тела над произвольно выбранным нулевым уровнем.
 или
или
 , где
, где — коэффициент трения скольжения,
— коэффициент трения скольжения, — сила нормальной реакции опоры.
— сила нормальной реакции опоры.

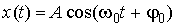 .
. - характеризует изменение какой-либо физической величины при колебаниях (смещение положения маятника из положения равновесия; напряжение на конденсаторе в колебательном контуре и т.д.), A - амплитуда колебаний,
- характеризует изменение какой-либо физической величины при колебаниях (смещение положения маятника из положения равновесия; напряжение на конденсаторе в колебательном контуре и т.д.), A - амплитуда колебаний,  - фаза колебаний,
- фаза колебаний,  - начальная фаза,
- начальная фаза,  - циклическая частота; величину
- циклическая частота; величину  называют также собственной частотой колебаний. Такое название подчеркивает, что эта частота определяется параметрами колебательной системы.
называют также собственной частотой колебаний. Такое название подчеркивает, что эта частота определяется параметрами колебательной системы.

 . Коэффициент γ носит название постоянной затухания. Он тоже имеет размерность частоты.
. Коэффициент γ носит название постоянной затухания. Он тоже имеет размерность частоты. , где
, где  — частота свободных колебаний.
— частота свободных колебаний.
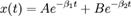 , где
, где 

 . Величина, обратная d, есть количество колебаний, которое пройдёт за время затухания τ.
. Величина, обратная d, есть количество колебаний, которое пройдёт за время затухания τ. .Консервативный гармонический осциллятор
.Консервативный гармонический осциллятор . Если ввести обозначения:
. Если ввести обозначения:  и заменить ускорение на вторую производную от координаты по времени, то получим следующее обыкновенное дифференциальное уравнение:
и заменить ускорение на вторую производную от координаты по времени, то получим следующее обыкновенное дифференциальное уравнение:
 ,
,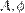 — произвольные постоянные, которые определяются из начальных условий.
— произвольные постоянные, которые определяются из начальных условий. и получим значение для константы:
и получим значение для константы:
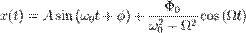
 ,
, материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса:
материальной точки относительно некоторого начала отсчёта определяется векторным произведением её радиус-вектора и импульса: 
 — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,
— радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,  — импульс частицы.
— импульс частицы. где
где  — радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.
— радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется. где
где  — импульс бесконечно малого точечного элемента системы).
— импульс бесконечно малого точечного элемента системы).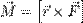 где
где  — радиус-вектор частицы.
— радиус-вектор частицы. , измеряющимся в градусах или радианах, угловой скоростью
, измеряющимся в градусах или радианах, угловой скоростью  (измеряется в рад/с) и угловым ускорением
(измеряется в рад/с) и угловым ускорением  (единица измерения — рад/с²).
(единица измерения — рад/с²). ,
, и его частота
и его частота  связаны соотношением
связаны соотношением  .
. ,
, .
. , где: mi — масса i-й точки, ri — расстояние от i-й точки до оси.
, где: mi — масса i-й точки, ri — расстояние от i-й точки до оси.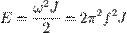 .
. .
. , то есть
, то есть  или
или 
 отсюда
отсюда  или
или  .
. Билет 24. Система уравнений движения абсолютно твёрдого тела в общем случае. Условия равновесия абсолютно твёрдого тела. Кинетическая энергия абсолютно твёрдого тела при произвольном движении
Билет 24. Система уравнений движения абсолютно твёрдого тела в общем случае. Условия равновесия абсолютно твёрдого тела. Кинетическая энергия абсолютно твёрдого тела при произвольном движении .
. . Ось может быть как реальной (неподвижной), так и мысленно проведенной через любую точку пространства.
. Ось может быть как реальной (неподвижной), так и мысленно проведенной через любую точку пространства.
 Запишем условие равновесия слоя жидкости толщиной dz, находящегося на высоте z от дна сосуда
Запишем условие равновесия слоя жидкости толщиной dz, находящегося на высоте z от дна сосуда Согласно уравнению, сила тяжести, действующая на выделенный слой жидкости, уравновешена силой, которая обусловлена разностью давлений жидкости на различной высоте. Согласно закону Гука давление жидкости определяется степенью ее деформации (всестороннего сжатия).
Согласно уравнению, сила тяжести, действующая на выделенный слой жидкости, уравновешена силой, которая обусловлена разностью давлений жидкости на различной высоте. Согласно закону Гука давление жидкости определяется степенью ее деформации (всестороннего сжатия). Для бесконечно малой толщины слоя dz можно приближенно положить
Для бесконечно малой толщины слоя dz можно приближенно положить Это обыкновенное дифференциальное уравнение первого порядка по аргументу z для нахождения неизвестной функции P(z). Решение этого уравнения с учётом что на поверхности жидкости давление P= имеет вид:
Это обыкновенное дифференциальное уравнение первого порядка по аргументу z для нахождения неизвестной функции P(z). Решение этого уравнения с учётом что на поверхности жидкости давление P= имеет вид:
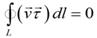 1. Ламинарное, где соседние слои жидкости скользят не перемешиваясь и поле скоростей является безвихревым в том смысле, что для любого контура L внутри жидкости для скорости выполняется равенство.
1. Ламинарное, где соседние слои жидкости скользят не перемешиваясь и поле скоростей является безвихревым в том смысле, что для любого контура L внутри жидкости для скорости выполняется равенство. 2. Турбулентное, хаотическое, где возникают завихрения и перемешивание соседних слоёв жидкости, характеристики движения жидкости меняются в пространстве и времени случайным образом, при этом поле скоростей является вихревым в том смысле, что для любого контура в жидкости.
2. Турбулентное, хаотическое, где возникают завихрения и перемешивание соседних слоёв жидкости, характеристики движения жидкости меняются в пространстве и времени случайным образом, при этом поле скоростей является вихревым в том смысле, что для любого контура в жидкости. Уравнение Бернулли
Уравнение Бернулли Согласно формуле Торричелли скорость истечения жидкости не зависит от её плотности и определяется высотой, с которой под действием силы тяжести жидкость спускается до уровня отверстия. В действительности скорость истечения жидкости зависит от размера и формы отверстия, вязкости жидкости и расхода жидкости, поэтому формула Торричелли является приближенной.
Согласно формуле Торричелли скорость истечения жидкости не зависит от её плотности и определяется высотой, с которой под действием силы тяжести жидкость спускается до уровня отверстия. В действительности скорость истечения жидкости зависит от размера и формы отверстия, вязкости жидкости и расхода жидкости, поэтому формула Торричелли является приближенной.
 Неидеальная жидкость – жидкость, в которой присутствуют вязкость и теплопередача. Вязкость жидкости, связывающая хаотическое тепловое движение молекул с макроскопическим движением жидкости, даёт возможность получить ответы на многие вопросы гидродинамики. Вязкость обеспечивает выравнивание скоростей движения соседних слоёв жидкости и приводит к появлению силы вязкого трения. В случае шарика радиусом, движущегося со скоростью в жидкости с вязкостью, на него действует сила вязкого трения, описываемая формулой Стокса.
Неидеальная жидкость – жидкость, в которой присутствуют вязкость и теплопередача. Вязкость жидкости, связывающая хаотическое тепловое движение молекул с макроскопическим движением жидкости, даёт возможность получить ответы на многие вопросы гидродинамики. Вязкость обеспечивает выравнивание скоростей движения соседних слоёв жидкости и приводит к появлению силы вязкого трения. В случае шарика радиусом, движущегося со скоростью в жидкости с вязкостью, на него действует сила вязкого трения, описываемая формулой Стокса.



 Запишем движение точки М в этих двух системах, задав это движение радиус-векторами и соответственно в системе k и k’:
Запишем движение точки М в этих двух системах, задав это движение радиус-векторами и соответственно в системе k и k’: - радиус-вектор, определяющий положение точки системы в системе отсчётаk.
- радиус-вектор, определяющий положение точки системы в системе отсчётаk. Спроецировав на координатные оси, запишем в скалярной форме:
Спроецировав на координатные оси, запишем в скалярной форме:

 (нерелятивистской механике): или
(нерелятивистской механике): или
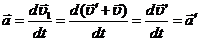 Скорость движения точки М (сигнала) в системе kʹ и в системе k различны
Скорость движения точки М (сигнала) в системе kʹ и в системе k различны Инвариантность ускорения(одинаковость во всех ИСО)
Инвариантность ускорения(одинаковость во всех ИСО)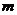
 Изучение медленных () механических движений показало, что = ',. Таким образом, масса и сила также являются инвариантами при переходе из одной ИСО в другую.
Изучение медленных () механических движений показало, что = ',. Таким образом, масса и сила также являются инвариантами при переходе из одной ИСО в другую. Принцип относительности в трактовке Эйнштейна: “Законы природы, по которым изменяются состояния физических систем, не зависят от того, к какой из инерциальных систем отсчёта относятся эти изменения”.
Принцип относительности в трактовке Эйнштейна: “Законы природы, по которым изменяются состояния физических систем, не зависят от того, к какой из инерциальных систем отсчёта относятся эти изменения”.

 Связь между импульсом и энергией:
Связь между импульсом и энергией: - формула Эйнштейна
- формула Эйнштейна - энергия покоя частицы (V= 0)
- энергия покоя частицы (V= 0)

 Кинетическая энергия частицы K определяется выражением:. В области малых скоростей, где и, кинетическая энергия:
Кинетическая энергия частицы K определяется выражением:. В области малых скоростей, где и, кинетическая энергия: Билет 30. Преобразования Лоренца. Изменение длины и интервала времени при переходе из одной инерциальной системы отсчёта в другую.
Билет 30. Преобразования Лоренца. Изменение длины и интервала времени при переходе из одной инерциальной системы отсчёта в другую.





 Изменение длины: Рассмотрим стержень, расположенный вдоль оси xʹ и покоящийся относительно системы Kʹ. Длина его в этой системе равна Для определения длины стержня в системе K нужно отметить координаты концов стержня в один и тот же момент времени t.
Изменение длины: Рассмотрим стержень, расположенный вдоль оси xʹ и покоящийся относительно системы Kʹ. Длина его в этой системе равна Для определения длины стержня в системе K нужно отметить координаты концов стержня в один и тот же момент времени t.










