Системой счисления называется совокупность приемов наименования и записи чисел.
В любой системе счисления выбираются некоторые символы – базисные числа, а все остальные числа получаются в результате каких-либо операций над базисными числами данной системы счисления.
Наиболее известным и широко применяемым является представление чисел с помощью арабских цифр от 0 до 9. Другой вариант – римская система счисления, использующая латинские буквы I (1), V (5), X (10), L (50), C (100), D (500) и M (1000).
Рассмотрим т.н. староримскую систему. В ней числа, отличные от базисных, образуются путём сложения.
Например, I – 1, II – 2, III – 3, IIII – 4, V – 5, VI – 6 и т.д.
Таким образом, значение базисного числа I не зависит от того, в какой позиции изображения числа оно находится.
В новой римской системе в качестве операций над базисными числами приняты не только сложение, но и вычитание. В частности, если младшая базисная цифра расположена до старшей (в качестве префикса), то она не прибавляется к общему результату, а вычитается из него. Например, IV – 4, а VI – 6; IX – 9, а XI – 11.
Основным недостатком подобных систем является сложность выполнения арифметических действий с числами. Так если сложение и вычитание в римской системе организовать можно, хотя и непросто, то построить аналог алгоритма умножения крайне затруднительно.
Другим вариантом систем счисления, к которым относится и используемая в повсеместной практике десятичная, являются позиционные системы. В них значение каждой цифры зависит от ее положения в изображении числа. В частности, в десятичной системе десять единиц каждого разряда объединяются в одну единицу соседнего старшего разряда. Таким образом, каждый разряд имеет вес, равный степени 10.
Например, число 528 можно представить как
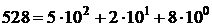
Здесь показатели степени основания системы счисления 10 соответствуют номерам десятичных разрядов цифр 5, 2 и 8, при условии, что цифры нумеруются справа налево, начиная с нуля.
Естественно, что десятичная система счисления является не единственной возможной позиционной системой. В случае выбора в качестве основания другого числа, отличного от 10, можно получить соответствующую систему счисления. В общем случае можно говорить о q-ичной системе, которая оперирует цифрами 0.. (q-1), а числа в ней образуются в соответствии с формулой:
 ,
,
где 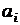 – q-ичная цифра в i -ом разряде числа; q – основание системы счисления, i – номер разряда; n – общее количество разрядов в числе.
– q-ичная цифра в i -ом разряде числа; q – основание системы счисления, i – номер разряда; n – общее количество разрядов в числе.
В цифровых вычислительных машинах наиболее широко применяется двоичная система счисления (q = 2). Двоичные числа образуются как последовательности лишь двух цифр – 0 и 1. Например, последовательность 11010 можно рассматривать как правильное двоичное число.
Для преобразования чисел из двоичной системы в десятичную необходимо выполнить вычисления по приведенной выше формуле в соответствии с правилами десятичной системы. Рассмотрим порядок преобразования числа 11010 в десятичную систему:

Обратное преобразование из десятичной системы в двоичную может быть выполнено аналогично (т.е. десятичное число необходимо разложить по указанной формуле, а вычисления произвести по правилам двоичной арифметики), однако есть более простой способ. Его суть заключается в следующем: необходимо последовательно делить преобразуемое число на основание системы счисления (число 2), при этом деление следует осуществлять нацело, а получающиеся остатки фиксировать. Например, рассмотрим преобразование числа 26 в двоичную систему:
26 / 2 = 13 – остаток 0
13 / 2 = 6 – остаток 1
6 / 2 = 3 – остаток 0
3 / 2 = 1 – остаток 1
1 / 2 = 0 – остаток 1
Процесс прекращается после того, как в результате очередного деления частное оказывается равным нулю. После этого искомое двоичное число получается как последовательность остатков, прочитанных в обратном порядке (в приведенном примере это будут считываемые снизу вверх 11010).
В таблице приведены первые 16 двоичных чисел:
Аналогичным образом можно осуществлять преобразование в систему с любым другим основанием. На практике помимо общеупотребимой десятичной и применяемой в вычислительной технике двоичной систем также используются восьмеричная и шестнадцатеричная системы. Основной особенностью последней является то, что для представления всех её базисных чисел (которых, очевидно, должно быть 16) не хватает 10 арабских цифр. Поэтому для базисных шестнадцатеричных чисел, соответствующих десятичным числам от 10 до 15, в этой системе используются латинские буквы A..F.
Аналогичным образом осуществляется перевод десятичного числа в шестнадцатеричное и обратно (пример).



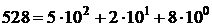
 ,
,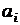 – q-ичная цифра в i -ом разряде числа; q – основание системы счисления, i – номер разряда; n – общее количество разрядов в числе.
– q-ичная цифра в i -ом разряде числа; q – основание системы счисления, i – номер разряда; n – общее количество разрядов в числе.



