Элементарная геометрия
Часть II
Лекции по специальному курсу
Элементарной математики
учебное пособие
для студентов педагогических вузов
Москва-2007
УДК… Печатается по решению кафедры высшей алгебры,
элементарной математики и методики преподавания
математики и редакционно-издательского совета МГОУ
Федяев О.И. Элементарная геометрия. Часть II Лекции по специальному курсу элементарной математики.
Учебное пособие для студентов педагогических вузов.
Материал учебного пособия разбит на части, называемые лекциями. Первые пять из них содержат подробную разработку теории подобий и движений евклидова пространства, а также исследование места и значения геометрических преобразований в геометрической системе Евклида. Достаточно подробно представлены примеры базовых геометрических понятий в свете свойств групп преобразований евклидова пространства. Шестая лекция посвящена теории геометрических построений, в частности, проблеме разрешимости конструктивной задачи циркулем и линейкой. Заключительная седьмая лекция посвящена общему обзору основных принципиально различных аксиоматических систем геометрии Евклида.
Научный редактор: проф. Рассудовская М.М.
Рецензенты: Птицына И.В. доц. к.ф.– м.н.
Куланин Е.Д. доц. к.ф. – м.н.
Предисловие
Одним из фундаментальных понятий геометрии является понятие о геометрическом преобразовании. Еще в ХIХ веке Ф.Клейн в своей вступительной лекции на должность профессора Гётингенского университета впервые достаточно четко определил роль геометрических преобразований, как, понятия, позволяющего структурировать геометрические системы на базе групп геометрических преобразований. С семидесятых годов двадцатого века элементы теории геометрических преобразований евклидова пространства становятся неотъемлемой частью школьного курса геометрии. Более того, ставится задача максимально обеспечить связь этой теории с традиционным материалом евклидовой геометрии, представленном в школьном курсе теориями равенства и подобия основных геометрических фигур, а так же элементами теории измерения величин. С одной стороны, перед творчески работающим учителем открывается большое поле для проявления самостоятельной творческой педагогической деятельности, а с другой, для ее результативности требуются глубокие знания в области не только теории геометрических преобразований, но и отчетливое понимание их роли, места и значения, прежде всего, в той геометрической системе, элементы которой составляют содержательную часть школьного курса математики. Именно эти две задачи в отношении теории движений и подобий пространства составляют цель первых пяти лекций настоящего пособия. При этом используемые методы решения поставленных задач иллюстрируют связь основных алгебраических понятий с содержательными фактами евклидовой геометрии. Шестая лекция настоящего пособия посвящена теории геометрических построений и, прежде всего, вопросу разрешимости конструктивной задачи циркулем и линейкой, который в полном объеме решается лишь при использовании алгебраических методов.
Заключительная лекция содержит три принципиально разных системы аксиом так называемой евклидовой геометрии, которые связываются с именами Д.Гильберта, Г.Вейля и Ф.Бахмана.
Лекция 1
Движения евклидова пространства.
Основные понятия.
Геометрическое преобразование – функция, определяемая на множестве точек пространства, значения которой являются точками этого пространства, хотя могут рассматриваться и отображения множеств других геометрических фигур, которые также относят к преобразованиям геометрическим. Например, так называемая корреляция, при которой точечное множество отображается на множество прямых. В школьном курсе геометрии рассматриваются именно точечные преобразования пространств, которые и называют преобразованиями геометрическими. Основное их свойство - взаимная однозначность отображения множества всех точек пространства на себя.
Первый вид преобразований евклидова пространства – это отображение пространства (как точечного множества) на себя, при котором произвольно взятой паре точек (А, В),соответствует такая пара точек (А¢, В¢) что отрезок А¢В¢ оказывается конгруэнтным отрезку АВ. Приведенное определение может несущественно трансформироваться в зависимости от выбора основных, неопределяемых понятий. Так, например, при условии, что основным понятием является «расстояние» (см., Геометрия 6-8, авторы А.Н.Колмогоров, А.Ф.Семенович, Р.С.Черкасов), условие конгруэнтности отрезок А¢В¢ и АВ заменяется условием равенства расстояний А¢В¢ и АВ. Мы в дальнейшем используем выше приведенный вариант определения, полагая при этом, что отношение «конгруэнтность» раскрывается в соответствующей системе аксиом (см. Д.Гильберт, Основания геометрии).
Взаимная однозначность определенного выше отображения пространства доказывается, что и позволяет заключить, что такое отображение есть геометрическое преобразование. Именно его называют «движением пространства». Использовались и другие термины для названия такого преобразования, например, «перемещение» (Геометрия 6-8, под ред. А.Н.Колмогорова), «конгруэнтное преобразование», «изометрия». Будем использовать установившееся в настоящее время название – движение, хотя это и можно подвергнуть критике, если учитывать повседневный или физический смысл этого понятия.
Рассмотрим некоторые основные свойства движений геометрического пространства, обозначая точку, соответствующую данной, той же буквой, но со штрихом.
Свойство 1: Если точка В лежит между точками А и С, то ей соответствующая точка В¢ лежит между точками А¢ и С¢, соответствующими точкам А и С.
Из условия следует, что АС @ АВ + ВС и А¢С¢ @ АС, А¢В¢ @ АВ,
В¢С¢ @ ВС.
Отсюда: А¢С¢ @ А¢В¢ + В¢С¢, а значит В¢ лежит между А¢ и С¢.
Свойство 2. Если В не лежит между А и С, то и В¢ не лежит между А¢ и С¢.
Если допустить противное, т.е В¢ лежит между А¢ и С¢, то
А¢С¢ @ А¢В¢ + В¢С¢. В силу конгруэнтностей А¢С¢ @ АС, А¢В¢ @ АВ и
В¢С¢ @ ВС получаем АС @ АВ + ВС. Отсюда В лежит между А и С. Следовательно, допущение неверно.
Следствиями доказанных выше свойств будут свойства, касающиеся преобразования основных геометрических фигур: прямой и плоскости, луча, полуплоскости, полупространства, отрезка.
Следствие 1. Образом прямой а при движении является прямая, которую
обозначаем а ¢.
Возьмем на а две различные точки А и В. Пусть их образы – точки А¢ и В¢.
В силу взаимной однозначности движения и различия точек А и В, А¢ и В¢ – различные точки. Они определяют единственную прямую, которую обозначим а ¢.
Пусть М принадлежит прямой а, тогда либо М лежит между А и В (обозначим это в виде записи  , либо М не лежит между А и В. В этом случае либо
, либо М не лежит между А и В. В этом случае либо  , либо
, либо  . В силу свойства 1 для М¢ будем иметь: либо
. В силу свойства 1 для М¢ будем иметь: либо  , либо
, либо  , либо
, либо  . Что означает принадлежность М¢ прямой а¢. Итак, образ всякой точки М прямой а, есть точка прямой а¢.
. Что означает принадлежность М¢ прямой а¢. Итак, образ всякой точки М прямой а, есть точка прямой а¢.
Точно также мы докажем, что всякая точка N¢ прямой а¢ есть образ точки N прямой а.
Именно в этом смысле мы и можем сказать, что движение отображает прямую а на прямую а¢.
Следствие 2. Образом плоскости a при движении пространства является плоскость, которую будем обозначать через a¢.
Доказательство проводится аналогично предыдущему:
1. А, В и С – три различные точки плоскости a, не принадлежащие одной прямой, А¢,В¢ и С¢ их образы. В этом случае эти точки не принадлежат одной прямой.
2. a¢ - плоскость, определяемая точками А¢,В¢ и С¢.
3. М – произвольная точка плоскости a и М¢ - ее образ.
а) М лежит на одной из прямых АВ, АС или ВС. Тогда М¢ - точка одной из прямых А¢В¢, А¢С¢ или В¢С¢, а значит точка плоскости a¢.
в) М не лежит ни на одной из прямых АВ, АС, ВС (рис.1).

Рис.1
Через М в a проводим прямую m, пересекающую АВ в точке N. Тогда m пересекает одну из прямых ВС или АС (аксиома Паша). Пусть для определенности – ВС в точке Р.
Образы точек N и Р принадлежат соответственно А¢В¢ и В¢С¢. Значит, прямая N¢Р¢, проходящая через М¢, принадлежит плоскости a¢. А поэтому точка М¢ принадлежит a¢.
Итак, образ всякой точки М плоскости a принадлежит плоскости a¢.
Пусть теперь М¢ - произвольная точка плоскости a¢, отличная от А¢, В¢ и С¢. Имеем две возможности:
а) М¢ - точка одной из прямых А¢В¢, А¢С¢ или В¢С¢. В этом случае ее прообраз точка М есть точка одной из прямых АВ,АС,ВС, а значит точка плоскости a.
в) М¢ отлична от точек А¢,В¢ и С¢. Проводим через М¢ прямую m¢ (рис.2). пересекающую две стороны треугольникаА¢В¢С¢, например, А¢В¢ в точке N¢ и В¢С¢ в точке Р¢. Прообразы точек N¢ и Р¢, точки N и Р есть точки сторон АВ и ВС треугольника АВС. Прямая NР есть прообраз прямой m¢ и проходит через М прообраз точки М¢. Но NР принадлежит плоскости a, а потому и точка М принадлежит a.

Рис.2
Вывод: Образ всякой точки М плоскости a есть точка М¢ плоскости a¢ и
обратно прообраз всякой точки М¢ плоскости a¢ есть точка М
плоскости a.
Именно это и означает, что плоскость a¢ есть образ плоскости a.
Аналогично можно доказать:
Следствие 3: Образом луча при движении пространства является луч.
Следствие 4: Образом полуплоскости при движении пространства является полуплоскость
.
Следствие 5: Образом полупространства при движении является
полупространство.
Предлагаем читателю провести эти доказательства в качестве упражнения.
Если отрезок трактуется как часть прямой, а не пара точек (как у Д.Гильберта), то нужно доказать и то, что образом отрезка при движении пространства является отрезок. Доказательство аналогично предыдущим и опирается на свойства 1 и 2.
Отметим еще без доказательства и свойства связанные с преобразованием медиатрисы отрезка и окружности.
Следствие 6: Если m – медиатрисса отрезка АВ, то m′ медиатрисса отрезка А′В′.
Следствие 7: Образом окружности (О, R) является окружность (О′, R).
Следствие 6 позволяет сделать заключение и о сохранении отношения ортогональности прямых, по крайней мере, для пересекающихся прямых: если а и b - пересекающиеся взаимно перпендикулярные прямые, то и их образы
а′ и b′ - взаимно пересекающиеся перпендикулярные прямые.
Следствие 7 дает возможность указать способ построения образа любой точки, по крайней мере, для случая движения в плоскости (в двумерном пространстве) при условии, когда известны три пары соответствующих друг другу точек (А,А′), (В,В′) и (С,С′), у которых А, В и С – точки не принадлежащие одной прямой. Покажем, как это делается.
Итак, А → А′, В → В′ и С → С′, причем А,В и С – три различные точки, не принадлежащие одной прямой. Пусть М - произвольная точка плоскости АВС.
Строим окружности (А′, АМ) и (В′, ВМ) (рис. 3).

Рис.3
Так как окружности (А, АМ) и (В, ВМ) по условию имеют общую точку, то и
(А′, АМ) и (В′, ВМ) имеют общую точку. Она единственна, если М принадлежит прямой АВ и таких точек две, если М не принадлежит АВ (на рисунке представлен этот вариант).
В первом случае единственная общая точка (А′, АМ) и (В′, ВМ) и есть образ точки М (обозначим его М′), во втором случае из двух точек пересечения окружностей (А′,АМ) (В′,ВМ) та есть образ точки М, которая принадлежит полуплоскости α′ с граничной прямой А′В′, которая является образом полуплоскости α с граничной прямой АВ. Какая из полуплоскостей с границей А′В′ есть α′ определяется с использованием взаимного расположения точек С и М относительно прямой АВ, которое при движении плоскости сохраняется. Иначе говоря С′ и М′ расположены относительно А′В′ также, как и точки С и М относительно прямой АВ.
Преобразования и, в частности, движения пространства могут выполняться последовательно: для какой-либо точки А ее образ при первом движении – А′, а при втором движении пространства образом А¢ является точка А′′. В этом случае автоматически определено отображение пространства, ставящее в соответствие точке А точку А′′. Это отображение, очевидно, будет геометрическим преобразованием пространства, которое произвольную пару точек (А, В) в рассматриваемом случае отображает на такую пару (А′′,В′′), что А′′В′′ @ АВ (следствие транзитивности отношения @).
Иначе говоря, последовательное выполнение двух движений дает движение пространства, которое и называют произведением первых двух. Произведение движений – алгебраическая операция на множестве всех движений пространства (любой размерности). Эту операцию называют умножением и, вводя обозначения для произведения движений, обозначают ее символом "◦".
Движения мы обозначаем греческой буквой d (дельта) с использованием как нижних, так и верхних индексов. Таким образом, если δ1 и δ2 – два движения, то их произведение обозначается δ2 ◦ δ1. Если произведение обозначено δ, то можно сделать запись δ = δ2 ◦ δ1. Так как преобразования суть функции, то произведение преобразований есть суперпозиция этих функций. При традиционном обозначении для функций будем иметь: δ2(δ1(х)) – произведение δ1 и δ2. Отсюда и сложился порядок записи сомножителей в представлении произведения преобразований в виде δ2 ◦ δ1: первый сомножитель справа, второй – слева. Отметим еще, что произведение движений некоммутативно в общем случае, поэтому δ2 ◦ δ1≠ δ1◦ δ2, хотя, как мы увидим в дальнейшем, для некоторых конкретных видов движений коммутативность умножения может и выполняться.
К движениям можно отнести и такое «преобразование», когда всякой точке А ставится в соответствие эта же точка А, иначе говоря все точки пространства «остаются на месте». Эта идеализация оправдывается тем, что при рассмотрении алгебраической структуры, элементами которой являются преобразования, пополнение множества преобразований этим идеальным элементом превращает его в алгебраическую структуру одного из важных для алгебры видов. Очевидно, что такое «преобразование» пространства естественно относится к движениям, т.к. всякий отрезок конгруэнтен самому себе. Это преобразование обозначим жирной цифрой 1. Ясно, что 1 играет роль нейтрального элемента по умножению для геометрических преобразований и движений пространства, в частности, для любого δ: δ ◦ 1 = 1 ◦ δ.
Всякое движение δ, отображающее произвольную точку А в точку А′, порождает отображение δ′ пространства на себя, отображающее всякую его точку А′ в точку А. В силу симметричности отношения конгруэнтности отрезков, это преобразование будет движением. Нетрудно понять, что это движение при умножении на первоначальное движение δ дает 1, иначе
δ′ ◦ δ = 1, точно также и δ ◦ δ′ = 1. В алгебре такой элемент алгебраической структуры называют обратным для рассматриваемого, т.е. δ′– движение обратное для δ. Используем для него стандартное обозначение δ-1.
Итак, можно теперь сделать
Вывод: Множество всех движений пространства (любой размерности) с
операцией умножения является группой, которую обозначим D.
Отметим теперь признак совпадения (тождественности) двух движений пространства, доказав его для случая движений плоскости. Для этого отметим
Свойство 3. Если движение пространства отображает каждую точку его симплекса в эту же точку, то движение пространства является тождественным.
В случае плоскости его симплексы – тройки неколлинеарных точек поэтому для такого пространства сформулированное выше утверждение приобретает вид: если два движения плоскости отображают каждую точку из числа трех точек плоскости, не принадлежащих одной прямой, в эту же точку, то движение плоскости является тождественным.
Итак, пусть (А, В, С) – тройка неколлинеарных (не принадлежащих одной прямой) точек некоторой плоскости и движение δ отображает А в А, В в В и С в С. Пусть М – произвольная точка плоскости α, которая определяется точками А, В и С. Если допустить, что точка М′, образ М, отлична от М, то прямая АВ – медиатрисса отрезка ММ′ и прямая АС - медиатрисса ММ′.
С одной стороны для отрезка медиатрисса единственна, но в силу сделанного допущения у отрезка ММ′ – две различные медиатрисы АВ и АС (точки А,В и С не принадлежат одной прямой по условию). Это противоречие, возникшее в следствии допущения различия М и М′, и заставляет принять:
М ≡ М′, таким образом, любая точка М плоскости α отображается в себя. Движение плоскости α тождественно.
Рассмотрим условие совпадения двух движений для случая плоскости.
Свойство 4. Если движения плоскости δ1 и δ2 отображают тройку
неколлинеарных точек А, В и С в одну и ту же тройку А′, В′ и С′, то эти движения совпадают, иначе δ1 = δ2.
Если δ2 отображает (А, В, С) в (А′, В′,С′), то δ2-1 отображает (А′,В′,С′) в
(А, В, С). Следовательно, (А, В, С)  (А, В, С). Согласно свойству 3 это означает, что δ2-1 ◦ δ1 = 1. Умножаем обе части этого равенства слева на δ2, получаем δ1 = δ2.
(А, В, С). Согласно свойству 3 это означает, что δ2-1 ◦ δ1 = 1. Умножаем обе части этого равенства слева на δ2, получаем δ1 = δ2.
Лекция 2
Виды движений плоскости
Если на плоскости фиксирована некоторая прямая а, то для точек плоскости можно определить отношение, которое называют симметрией относительно прямой а: точка А′ симметрична точке А относительно а, если а является медиатриссой отрезка АА′. Пополнив это условие симметрии точек относительно прямой соглашением, что каждая точка прямой а симметрична самой себе, получаем возможность с помощью отношения симметрии задать отображение плоскости на себя, при котором всякой точке А плоскости соответствует точка А′, симметричная А относительно некоторой фиксированной прямой а. Такое отображение называют осевой симметрией в плоскости. Будем в дальнейшем обозначать это отображение σа. Ясно, что всякое σа является геометрическим преобразованием плоскости (двумерного пространства). Обратим внимание на то, что для всякой σа в плоскости существует бесконечное множество точек, каждая из которых соответствует сама себе. Такие точки называют двойными или неподвижными. Неподвижными точками плоскости для всякой осевой симметрии σа являются все точки прямой а, оси симметрии, и только эти точки плоскости. Осевые симметрии существуют, поскольку со всякой прямой а связано отношение симметрии для точек плоскости. В этом смысле можно говорить, что осевая симметрия σа однозначно определяется заданием прямой а, ее оси симметрии.
Очевидно и то, что осевая симметрия является движением плоскости, поскольку для любых точек А и В их образы А′ и В′ таковы, что А′В′ @ АВ.
Из того, что для любой точки А, если А  А′, то А¢
А′, то А¢  А, следует s а◦ sа = 1.
А, следует s а◦ sа = 1.
Такие преобразования называют инволютивыми.
Поскольку осевая симметрия есть движение, произведение любого конечного числа осевых симметрий есть движение. Покажем теперь, что верно и обратное.
Теорема: Всякое движение плоскости можно представить произведением
осевых симметрий, причем для такого представления достаточно не более трех симметрий.
Возьмем три неколлинеарные точки А, В, С. Пусть их образами при данном движении δ являются А′, В′, С′ соответственно.
1. Если А=А′, В=В′ и С=С′, то согласно свойству 4 δ есть тождественное преобразование. В этом случае для любой прямой а σа ◦ σа = 1, а потому данное движение δ представимо произведением двух осевых симметрий, т.е. δ = σа ◦ σа.
2. Пусть δ ≠ 1, тогда из трех пар точек (А, А′), (В, В′) и (С, С′), по крайней мере, одна есть пара различных точек. Пусть А ≠ А′. Существует медиатриса отрезка АА′, которую обозначим а. σа отображает А → А′, В→ В1 и С → С1.
Может случиться:
1) В1 = В′ и С1 = С′, 2) В1 = В′, но С1 ≠ С′ и 3) В1 ≠ В′ и С1 ≠ С′
Рассмотрим последовательно эти три случая.
1). В1 = В′ и С1 = С′. В этом случае А 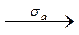 А¢, В
А¢, В 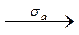 В¢ и
В¢ и
С 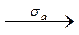 С¢. В силу свойства 4 в этом случае d = sа. Возьмем произвольную прямую b и соответствующую ей осевую симметрию sb.
С¢. В силу свойства 4 в этом случае d = sа. Возьмем произвольную прямую b и соответствующую ей осевую симметрию sb.
d = sа ◦ 1 = sа◦ (sb ◦sb). Видим, что δ представлено произведением трех симметрий: sа◦ sb ◦sb.
Теорема для этого случая доказана.
2). В1 = В′, но С1 ≠ С′ (рис.4). В этом случае прямая А′В′ – медиатрисса отрезка С1С′, т.к. А¢С1 @ А¢С¢ и В¢С1 @ В¢С¢. Поэтому С′ симметрична С1
относительно прямой А′ В′. Обозначив прямую А′В′ буквой b, получаем:
(А, В, С) 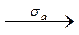 (А′, В′, С1)
(А′, В′, С1)  (А′,В′,С′), т.е.
(А′,В′,С′), т.е.
(А,В,С)  (А′,В′,С′).
(А′,В′,С′).
Согласно свойству 4 d = sb◦ sа.
Как видим и в этом случае теорема доказана.

Рис.4
3). В1 ≠ В′ и С1 ≠ С′. В этом случае существует медиатрисса отрезка В1 В′, которую обозначим через b (рис.5).
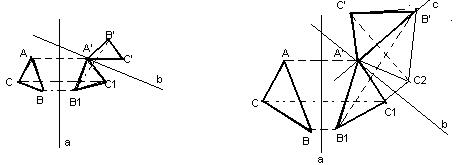
Рис.5
Осевая симметрия sb отображает А′ в А′, т.к. b проходит через А′
(А′ равноудалена от В1 и В′), В1 переходит в В′, а С1 в С2.
Возможны два случая: С2=С′ (левая часть рис.5) или С2 ≠ С′ (правая часть рис.5). В первом случае имеем:
А  А′
А′  А′, В
А′, В  В1
В1  В′ и
В′ и
С  С1
С1  С′, что согласно свойству 4 означает: δ=σb ◦ σa.
С′, что согласно свойству 4 означает: δ=σb ◦ σa.
Во втором случае существует медиатриса отрезка С2С′, которую обозначаем с. В этом случае имеем:
А  А′
А′  А′
А′  А′, т.к. А′ принадлежит и b и с.
А′, т.к. А′ принадлежит и b и с.
В  В1
В1  В′
В′  В′, т.к. с есть прямая А′В′, т.е. В′Î с.
В′, т.к. с есть прямая А′В′, т.е. В′Î с.
С  С1
С1  С2
С2  С′, т.к. с - медиатриса отрезка С2 С′.
С′, т.к. с - медиатриса отрезка С2 С′.
Таким образом, А  А′, В
А′, В  В′, С
В′, С  С′.
С′.
Согласно свойству 4 это означает, что d = sc ◦ sb ◦ sa.
Видим, что возможны два случая представления δ:
1. δ = σb ◦ σa, включая случай δ = σa ◦ σa;
2. δ = σc ◦ σb ◦ σa.
Таким образом, теорема доказана полностью.
Заметим, что теорема легко обобщается на случай пространств любой размерности. В частности, для трехмерного пространства δ представимо произведением плоскостных симметрий, причем возможны три случая таких представлений:
1. произведением двух симметрий,
2. произведением трех симметрий
3. произведением четырех симметрий.
Если обозначить плоскостную симметрию в виде  , где
, где
α – плоскость, относительно которой рассматриваются пары симметричных точек пространства, то эти случаи предстанут в виде:
1. δ = σb ◦ σa, включая совпадение β и α;
2. δ = σg ◦ σb ◦ σa;
3. δ = σn ◦ σg ◦ σb ◦ σ a .
Доказанная теорема позволяет классифицировать движения плоскости и перечислить все их возможные виды.
Сделаем обзор этой классификации для случая плоскости.
С точки зрения рассмотренного выше представления движений имеем два вида движений: движения, представимые произведениями двух осевых симметрий, и движения представимые произведениями трех осевых симметрий.
Рассмотрим первый вид: δ = σb ◦ σa. Прямые а и b могут быть параллельны, включая случай их совпадения, или прямые а и b пересекаются в некоторой точке.
Первый случай а ║ b. Если при этом а = b, то σb ◦ σa = 1.
Пусть а и b – различные прямые. Возьмем две различные точки М и N (рис.6) Так как ММ′ и NN′ перпендикулярны к а и b, то ММ′║N N′.


Докажем, что и М′N′║МN, методом «от противного». Допустим, что прямые МN и М′N′ пересекаются в некоторой точке L. Поведем через L прямую l
перпендикулярно к а и b. Тогда точка L может рассматриваться как точкa пересечения прямых МN и l или М′N′ и l.
Имеем: L = MN ∩ l  M′N′ ∩ l = L
M′N′ ∩ l = L
Иначе говоря, L  L или L
L или L  L1
L1  L.
L.
Это означает, что а и b одновременно являются медиатрисами LL1, что противоречит свойству медиатриссы, как серединного перпендикуляра отрезка. Противоречие оказалось следствием допущения «прямые MN и M′N′ пересекаются». Значит, его нужно отбросить, иначе говоря принять, что M′N′║MN.
Итак, рассматриваемый случай δ характеризуется двумя свойствами:
1. М′М ║ N′N и 2. M′N′║MN для любой пары точек (М, N) плоскости. Такое преобразование называют параллельным переносом. Итак, параллельным переносом называют геометрическое преобразование пространства, при котором любой паре точек (М, N) соответствует такая пара точек (М′, N′), что: 1. ММ′║ NN′ и 2. М′N′║МN.
Если для некоторой точки А указан ее образ А¢, то для любой точки пространства ее образ может быть найден конструктивно, построением образа точки циркулем и линейкой.
Итак, пусть А → А′, М – произвольная точка пространства. Рассмотрим два случая положения М относительно прямой АА′.
1.М Ï АА′ (рис.7). Так как для М′ ММ′║ АА′ и А′М′║АМ, то М′ – точка
пересечения прямых параллельных АА′ и АМ и проходящих соответственно через точки М и А′. Отсюда основные шаги построения
точки М:
 1.построение прямой m, проходящей через М параллельно АА′;
1.построение прямой m, проходящей через М параллельно АА′;
Рис.7
2. построение прямой а ′, проходящей через А′ параллельно АМ.
2. М Î АА′(рис.8). Построение М′ такое же как и в первом случае, повторенное дважды:
 Рис.8
Рис.8
сначала строится N′ для точки N, не лежащей на АА′, затем строится М′ с опорой на пару точек (N, N′).
В этом случае лишь возникает естественный вопрос: не зависит ли при этом конечный результат построения, точка М′, от выбора точки N? Ответ положительный: не зависит.
Основанием этого результата является теорема Дезарга. Представим это на рисунке (рис.9)

 1.∆ АNР и ∆ А′N′Р′ – в условиях теоремы Дезарга. Поэтому N′Р′ ║ NР.
1.∆ АNР и ∆ А′N′Р′ – в условиях теоремы Дезарга. Поэтому N′Р′ ║ NР.
2. ∆ МNР и ∆ М′N′Р′ - в условиях теоремы Дезарга, а потому МР ║ М′Р′.
При построении образа точки М с опорой на пару (Р, Р′) через Р′ проводится прямая, параллельная РМ. Но таковой по доказанному будет именно прямая Р′М′.
Именно возможность построения образа любой точки пространства при условии задания пары соответствующих друг другу точек (А, А′) и имеют в виду говоря, что параллельный перенос определяется заданием пары соответствующих друг другу точек.
Отметим еще, что множество параллельных переносов пространства (любой размерности) включая 1, с операцией умножения (как их последовательного выполнения) представляет группу и при том коммутативную (см.рис.10). Стрелки на рисунке указывают два способа последовательного выполнения двух параллельных переносов.







 А¢ Будем параллельные переносы обозначать греческой буквой τ (тау) при необходимости с индексами. Группу параллельных переносов обозначим латинской буквой T.
А¢ Будем параллельные переносы обозначать греческой буквой τ (тау) при необходимости с индексами. Группу параллельных переносов обозначим латинской буквой T.
Рис. 10
Рассмотрим второй случай а ∩ b = О.
В этом случае, прежде всего, можно отметить, что точка О – двойная (неподвижная) точка преобразования σb ◦ σa. Покажем, что никаких других двойных точек в плоскости прямых а и b нет. Допустим противное, некоторая точка Р, отличная от О – двойная, т.е. Р  Р.Положим, что Р Ï а, тогда Р
Р.Положим, что Р Ï а, тогда Р  Р1 и Р ≠ Р1× Р1
Р1 и Р ≠ Р1× Р1  Р, иначе не имело бы места сделанное допущение. Для пары (Р, Р1) а и b – медиатриссы отрезкаРР1. Получили противоречие: с одной стороны, известно, что у отрезка медиатриса единственна, а в силу сделанного допущения отрезок обладает двумя медиатрисами. Это заставляет нас отбросить допущение, т.е. нет двойных точек, отличных от О и не принадлежащих а. Точно также получается, что среди не принадлежащих b так же нет двойных точек относительно рассматриваемого преобразования.
Р, иначе не имело бы места сделанное допущение. Для пары (Р, Р1) а и b – медиатриссы отрезкаРР1. Получили противоречие: с одной стороны, известно, что у отрезка медиатриса единственна, а в силу сделанного допущения отрезок обладает двумя медиатрисами. Это заставляет нас отбросить допущение, т.е. нет двойных точек, отличных от О и не принадлежащих а. Точно также получается, что среди не принадлежащих b так же нет двойных точек относительно рассматриваемого преобразования.
Предположим теперь, что Р Î а (или b), но отлична от О.
Тогда Р  Р
Р  Р′, причем Р ¹ Р′, т.к. Р Ï b, если Р Î а. Таким образом, Р в этом случае не двойная точка. Итак, О – единственная неподвижная точка плоскости относительно движения σb ◦ σa.
Р′, причем Р ¹ Р′, т.к. Р Ï b, если Р Î а. Таким образом, Р в этом случае не двойная точка. Итак, О – единственная неподвижная точка плоскости относительно движения σb ◦ σa.
Отсюда следует, что для любой точки М, отличной от О, М′ такова, что
ОМ′ @ ОМ. Второе: для любой пары точек (М, N) пара соответствующих точек (М′, N′) такова, что ÐМОМ′ @ ÐNОN′, т.к. каждый из них конгруэнтен удвоенному углу между прямыми а и b (рис.11).
Заметим, что доказательство этого утверждения должно использовать операцию сложения углов. Наглядно ясная процедура формализуется весьма непросто.

Рис.11
Таким образом, в наглядном смысле каждая точка плоскости, поворачивается относительно точки О на один и тот же угол, равный удвоенному углу между прямыми а и b. Именно поэтому для названия этого преобразования плоскости используется термин «вращение».
Итак, σb ◦ σa при условии пересечения прямых а и b является вращением плоскости с центром О (точка пересечения прямых а и b). Обозначать вращение плоскости будем греческой буквой w (омега) с нижним индексом, обозначающим центр вращения. Вращение это движение плоскости с единственной инвариантной точкой, называемой центром вращения.
Обратимся теперь ко второму случаю, когда движение представляется произведением трех осевых симметрий: δ = σс ◦ σb ◦ σa. Делим этот случай на два, полагая в основу условие принадлежности трех прямых одному пучку прямых. Итак, первый случай: прямые а, b и с принадлежат одному пучку, т.е. либо все три параллельны, либо все три проходят через одну точку.
Пусть а ║ b ║ с. Если а = b или b = с, то σс ◦ σb ◦ σa = σс ◦ 1 = σс, либо
σс ◦ σb ◦ σa = 1 ◦ σа = σa. Таким образом, в этих случаях произведение трех симметрий есть симметрия. Рассматриваем общий случай, когда а ¹ b и b ¹ с. Если прямая l не перпендикулярна и не параллельна осям симметрии, то ее образ l′ не параллелен l. Иначе говоря l и l′ пересекаются.

Рис.12
Обозначим точку пересечения буквой L (рис.12).
l  l1
l1  l2
l2  l′, l ║ l2,l2 не параллельна l′. Поэтому l и l′ не параллельны.
l′, l ║ l2,l2 не параллельна l′. Поэтому l и l′ не параллельны.
Проводим через точку L прямую n, перпендикулярно а, b и с.
n  n
n  n
n  n, т.е. n
n, т.е. n 



 , либо М не лежит между А и В. В этом случае либо
, либо М не лежит между А и В. В этом случае либо  , либо
, либо  . В силу свойства 1 для М¢ будем иметь: либо
. В силу свойства 1 для М¢ будем иметь: либо  , либо
, либо  , либо
, либо  . Что означает принадлежность М¢ прямой а¢. Итак, образ всякой точки М прямой а, есть точка прямой а¢.
. Что означает принадлежность М¢ прямой а¢. Итак, образ всякой точки М прямой а, есть точка прямой а¢.


 (А, В, С). Согласно свойству 3 это означает, что δ2-1 ◦ δ1 = 1. Умножаем обе части этого равенства слева на δ2, получаем δ1 = δ2.
(А, В, С). Согласно свойству 3 это означает, что δ2-1 ◦ δ1 = 1. Умножаем обе части этого равенства слева на δ2, получаем δ1 = δ2. А′, то А¢
А′, то А¢ 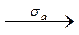 А¢, В
А¢, В  (А′,В′,С′), т.е.
(А′,В′,С′), т.е. (А′,В′,С′).
(А′,В′,С′).

 А′
А′  А′, В
А′, В  А′, т.к. А′ принадлежит и b и с.
А′, т.к. А′ принадлежит и b и с. А′, В
А′, В  , где
, где

 M′N′ ∩ l = L
M′N′ ∩ l = L 1.построение прямой m, проходящей через М параллельно АА′;
1.построение прямой m, проходящей через М параллельно АА′; Рис.8
Рис.8
 1.∆ АNР и ∆ А′N′Р′ – в условиях теоремы Дезарга. Поэтому N′Р′ ║ NР.
1.∆ АNР и ∆ А′N′Р′ – в условиях теоремы Дезарга. Поэтому N′Р′ ║ NР.






 А¢ Будем параллельные переносы обозначать греческой буквой τ (тау) при необходимости с индексами. Группу параллельных переносов обозначим латинской буквой T.
А¢ Будем параллельные переносы обозначать греческой буквой τ (тау) при необходимости с индексами. Группу параллельных переносов обозначим латинской буквой T. Р.Положим, что Р Ï а, тогда Р
Р.Положим, что Р Ï а, тогда Р  Р1 и Р ≠ Р1× Р1
Р1 и Р ≠ Р1× Р1  Р, иначе не имело бы места сделанное допущение. Для пары (Р, Р1) а и b – медиатриссы отрезкаРР1. Получили противоречие: с одной стороны, известно, что у отрезка медиатриса единственна, а в силу сделанного допущения отрезок обладает двумя медиатрисами. Это заставляет нас отбросить допущение, т.е. нет двойных точек, отличных от О и не принадлежащих а. Точно также получается, что среди не принадлежащих b так же нет двойных точек относительно рассматриваемого преобразования.
Р, иначе не имело бы места сделанное допущение. Для пары (Р, Р1) а и b – медиатриссы отрезкаРР1. Получили противоречие: с одной стороны, известно, что у отрезка медиатриса единственна, а в силу сделанного допущения отрезок обладает двумя медиатрисами. Это заставляет нас отбросить допущение, т.е. нет двойных точек, отличных от О и не принадлежащих а. Точно также получается, что среди не принадлежащих b так же нет двойных точек относительно рассматриваемого преобразования. Р
Р 

 l′, l ║ l2,l2 не параллельна l′. Поэтому l и l′ не параллельны.
l′, l ║ l2,l2 не параллельна l′. Поэтому l и l′ не параллельны. n
n  n, т.е. n
n, т.е. n 



