Рекуррентные соотношения
В математике довольно часто используется метод сведения данной задачи к задаче с меньшим количеством предметов.
Опр. Метод сведения к аналогичной задаче для меньшего числа предметов называется методом рекуррентных соотношений.
Пользуясь рекуррентным соотношением можно свести задачу об n предметах к задаче об n-1 предметах, потом к задаче об n-2 предметах и т.д. Последовательно уменьшая число предметов, доходим до задачи, которую легко решить. Во многих случаях удается получить из рекуррентного соотношения явную формулу для решения задачи.
Пример. Задача Фибоначчи
В 1202 г. итальянский математик Фибоначчи сформулировал следующую задачу:
Пара кроликов приносит раз в месяц приплод из 2-х крольчат (самки и самца), причем новорожденные крольчата через 2 месяца после рождения уже приносят приплод. Сколько кроликов появится через год, если в начале года была одна пара кроликов?
Решение.
Обозначим через F(n) – количество пар кроликов по истечении n месяцев с начала года. Видно, что через (n+1) месяцев будут эти F(n) пар и еще столько новорожденных пар кроликов сколько было в конце месяца (n-1), т.е. еще F(n-1) пар кроликов.
Т.о. справедливо рекуррентное соотношение
F(n+1) = F(n) + F(n-1)
Опр. ЧислаF(n) называют числами Фиббоначи.
Бывают комбинаторные задачи, в которых приходится составлять не одно рекуррентное соотношение, а систему соотношений.
Пример. Затруднение мажордома
Однажды мажордом короля Артура обнаружил, что к обеду за круглым столом приглашено 6 пар враждующих рыцарей. Сколькими способами их можно рассадить так, чтобы никакие два врага не сидели рядом?
Опр. Рекуррентным соотношением k-того порядка называется соотношение позволяющее выразить  через
через 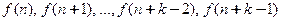 .
.
Пример.
f(n+2) = f(n) f(n+1) - 3f2(n+1) +1 – рекуррентное соотношение 2-го порядка
f(n+3) = 6f(n) f(n+2) + f(n+1) – рекуррентное соотношение 3-го порядка
Если задано рекуррентное соотношение k-го порядка, то ему удовлетворяет бесконечно много последовательностей, т.к. первые k элементов последовательности можно задать совершенно произвольно (между ними нет никаких соотношений). Однако, если первые k элементов заданы, то все остальные элементы определяются совершенно однозначно.
Пользуясь рекуррентными соотношениями и начальными членами, можно один за другим выписывать члены последовательности, причем рано или поздно мы получим любой ее член. Однако на практике часто требуется узнать только один определенный член последовательности. В таких случаях удобнее иметь явную формулу для n-го члена последовательности.
Опр. Последовательность  называется частным решением рекуррентного соотношения, если подстановка общего члена последовательности в рекуррентное соотношение превращает его в тождество.
называется частным решением рекуррентного соотношения, если подстановка общего члена последовательности в рекуррентное соотношение превращает его в тождество.
Пример.
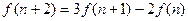
Будет ли  являться частным решением этого соотношения?
являться частным решением этого соотношения?

Следовательно,  - частное решение рекуррентного соотношения.
- частное решение рекуррентного соотношения.
Опр. Общим решением рекуррентного соотношения k- того порядка называется решение, содержащее k произвольных постоянных, путём подбора которых можно получить любое решение данного соотношения.
Пример.

Будем искать решение в виде: 


 - характеристическое уравнение.
- характеристическое уравнение.

 - частные решения.
- частные решения.
 - общее решение.
- общее решение.
Найдем С1 и С2, используя начальные условия.
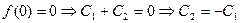

 - формула общего члена последовательности Фибоначчи.
- формула общего члена последовательности Фибоначчи.
Для решения рекуррентных соотношений общих правил нет. Однако, существует достаточно часто встречающийся класс соотношений, решаемый единообразным методом.
Доказательство.


Умножим первое равенство на А, второе на В и сложим вновь получившиеся равенства.

что и требовалось доказать
Лемма2. Если число х1 является корнем характеристического уравнения (4), то последовательность 1, х1, х12, …, х1n-1,… является решением рекуррентного соотношения (3).
Доказательство.
1) 
x2=px+q.
По лемме2, если  - корни характеристического уравнения, то
- корни характеристического уравнения, то  - решения рекуррентного соотношения (3). По лемме1
- решения рекуррентного соотношения (3). По лемме1  - также будет решением рекуррентного соотношения (3).
- также будет решением рекуррентного соотношения (3).
Подставим в (3) равенство  , а также учтем, что по теореме Виета:
, а также учтем, что по теореме Виета:
p=x1+x2, q= –x1x2:

То есть  обращает в тождество уравнение (3).
обращает в тождество уравнение (3).
Проверим, существуют ли такие C1 и C2.
Пусть f(0)=a, f(1)=b. Тогда:
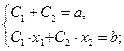
 Þ для любых a, b система имеет единственное решение Þ C1 и C2 можно найти Þ формула верна.
Þ для любых a, b система имеет единственное решение Þ C1 и C2 можно найти Þ формула верна.
2) 
 по теореме Виета
по теореме Виета 

Покажем, что  будет решением рекуррентного соотношения.
будет решением рекуррентного соотношения.

То есть  обращает в тождество уравнение (3). Проверим, существуют ли такие C1 и C2.
обращает в тождество уравнение (3). Проверим, существуют ли такие C1 и C2.


 - общее решение, т.к. C1 и C2 можно найти.
- общее решение, т.к. C1 и C2 можно найти.
Рекуррентные соотношения
В математике довольно часто используется метод сведения данной задачи к задаче с меньшим количеством предметов.
Опр. Метод сведения к аналогичной задаче для меньшего числа предметов называется методом рекуррентных соотношений.
Пользуясь рекуррентным соотношением можно свести задачу об n предметах к задаче об n-1 предметах, потом к задаче об n-2 предметах и т.д. Последовательно уменьшая число предметов, доходим до задачи, которую легко решить. Во многих случаях удается получить из рекуррентного соотношения явную формулу для решения задачи.
Пример. Задача Фибоначчи
В 1202 г. итальянский математик Фибоначчи сформулировал следующую задачу:
Пара кроликов приносит раз в месяц приплод из 2-х крольчат (самки и самца), причем новорожденные крольчата через 2 месяца после рождения уже приносят приплод. Сколько кроликов появится через год, если в начале года была одна пара кроликов?
Решение.
Обозначим через F(n) – количество пар кроликов по истечении n месяцев с начала года. Видно, что через (n+1) месяцев будут эти F(n) пар и еще столько новорожденных пар кроликов сколько было в конце месяца (n-1), т.е. еще F(n-1) пар кроликов.
Т.о. справедливо рекуррентное соотношение
F(n+1) = F(n) + F(n-1)
Опр. ЧислаF(n) называют числами Фиббоначи.
Бывают комбинаторные задачи, в которых приходится составлять не одно рекуррентное соотношение, а систему соотношений.
Пример. Затруднение мажордома
Однажды мажордом короля Артура обнаружил, что к обеду за круглым столом приглашено 6 пар враждующих рыцарей. Сколькими способами их можно рассадить так, чтобы никакие два врага не сидели рядом?
Опр. Рекуррентным соотношением k-того порядка называется соотношение позволяющее выразить  через
через 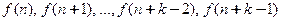 .
.
Пример.
f(n+2) = f(n) f(n+1) - 3f2(n+1) +1 – рекуррентное соотношение 2-го порядка
f(n+3) = 6f(n) f(n+2) + f(n+1) – рекуррентное соотношение 3-го порядка
Если задано рекуррентное соотношение k-го порядка, то ему удовлетворяет бесконечно много последовательностей, т.к. первые k элементов последовательности можно задать совершенно произвольно (между ними нет никаких соотношений). Однако, если первые k элементов заданы, то все остальные элементы определяются совершенно однозначно.
Пользуясь рекуррентными соотношениями и начальными членами, можно один за другим выписывать члены последовательности, причем рано или поздно мы получим любой ее член. Однако на практике часто требуется узнать только один определенный член последовательности. В таких случаях удобнее иметь явную формулу для n-го члена последовательности.
Опр. Последовательность  называется частным решением рекуррентного соотношения, если подстановка общего члена последовательности в рекуррентное соотношение превращает его в тождество.
называется частным решением рекуррентного соотношения, если подстановка общего члена последовательности в рекуррентное соотношение превращает его в тождество.
Пример.
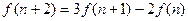
Будет ли  являться частным решением этого соотношения?
являться частным решением этого соотношения?

Следовательно,  - частное решение рекуррентного соотношения.
- частное решение рекуррентного соотношения.
Опр. Общим решением рекуррентного соотношения k- того порядка называется решение, содержащее k произвольных постоянных, путём подбора которых можно получить любое решение данного соотношения.
Пример.

Будем искать решение в виде: 


 - характеристическое уравнение.
- характеристическое уравнение.

 - частные решения.
- частные решения.
 - общее решение.
- общее решение.
Найдем С1 и С2, используя начальные условия.
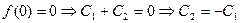

 - формула общего члена последовательности Фибоначчи.
- формула общего члена последовательности Фибоначчи.
Для решения рекуррентных соотношений общих правил нет. Однако, существует достаточно часто встречающийся класс соотношений, решаемый единообразным методом.



 через
через 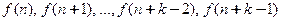 .
. называется частным решением рекуррентного соотношения, если подстановка общего члена последовательности в рекуррентное соотношение превращает его в тождество.
называется частным решением рекуррентного соотношения, если подстановка общего члена последовательности в рекуррентное соотношение превращает его в тождество.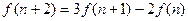
 являться частным решением этого соотношения?
являться частным решением этого соотношения?




 - характеристическое уравнение.
- характеристическое уравнение.
 - частные решения.
- частные решения. - общее решение.
- общее решение.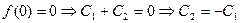

 - формула общего члена последовательности Фибоначчи.
- формула общего члена последовательности Фибоначчи.



 - корни характеристического уравнения, то
- корни характеристического уравнения, то  - решения рекуррентного соотношения (3). По лемме1
- решения рекуррентного соотношения (3). По лемме1  - также будет решением рекуррентного соотношения (3).
- также будет решением рекуррентного соотношения (3).
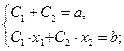
 Þ для любых a, b система имеет единственное решение Þ C1 и C2 можно найти Þ формула верна.
Þ для любых a, b система имеет единственное решение Þ C1 и C2 можно найти Þ формула верна.
 по теореме Виета
по теореме Виета 

 будет решением рекуррентного соотношения.
будет решением рекуррентного соотношения.
 обращает в тождество уравнение (3). Проверим, существуют ли такие C1 и C2.
обращает в тождество уравнение (3). Проверим, существуют ли такие C1 и C2.

 - общее решение, т.к. C1 и C2 можно найти.
- общее решение, т.к. C1 и C2 можно найти.


