Определение 8.1. Матрица  с неотрицательными компонентами называется продуктивной, если для любого
с неотрицательными компонентами называется продуктивной, если для любого 
 существует неотрицательное решение
существует неотрицательное решение 
 уравнения
уравнения
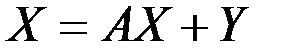 . (8.1)
. (8.1)
В этом случае модель Леонтьева (8.1), определяемая матрицей А, также называется продуктивной.
Итак, модель Леонтьева продуктивна, если любой вектор 
 конечного потребления можно получить при подходящем валовом выпуске
конечного потребления можно получить при подходящем валовом выпуске 
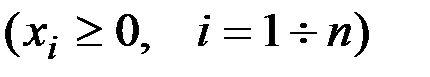 .
.
Однако, можно доказать, что нет необходимости требовать существования решения  уравнения (8.1) для любого вектора
уравнения (8.1) для любого вектора 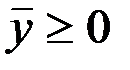 . Достаточно, чтобы такое решение существовало хотя бы для одного вектора
. Достаточно, чтобы такое решение существовало хотя бы для одного вектора  . Условимся в дальнейшем называть вектор
. Условимся в дальнейшем называть вектор  положительным, если все компоненты этого вектора строго положительны.
положительным, если все компоненты этого вектора строго положительны.
Первый критерий продуктивности. Если  и для некоторого положительного вектора
и для некоторого положительного вектора  уравнение (8.1) имеет неотрицательное решение
уравнение (8.1) имеет неотрицательное решение 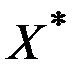 , где
, где  , то матрица
, то матрица  продуктивна.
продуктивна.
Замечание. На самом деле при заданных условиях решение получается положительное, т.е.  . Это следует из уравнения (8.1)
. Это следует из уравнения (8.1)  и
и 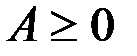 ,
,  ,
,  .
.
Запишем уравнение Леонтьева (8.1) следующим образом:
 , (8.2)
, (8.2)
где  – единичная матрица. Будем искать матрицу, обратную по отношению к матрице
– единичная матрица. Будем искать матрицу, обратную по отношению к матрице  .
.
Понятно, что если обратная матрица 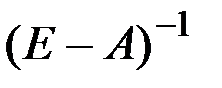 существует, то из уравнения (8.2) следует, что
существует, то из уравнения (8.2) следует, что
 . (8.3)
. (8.3)
Отсюда вытекает следующее более эффективное условие продуктивности.
Второй критерий продуктивности. Матрица  продуктивна тогда и только тогда, когда матрица
продуктивна тогда и только тогда, когда матрица 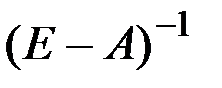 существует и неотрицательна.
существует и неотрицательна.
Доказательство этого утверждения приведено в [6].Матрица 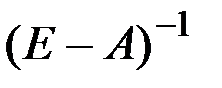 называется матрицей полных затрат.
называется матрицей полных затрат.
Пример 8.1. Исследуем на продуктивность матрицу
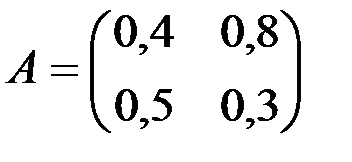 .
.
Решение. Найдём матрицу
 .
.
Вычислим ее определитель:

Союзная матрица  имеет вид
имеет вид  . Тогда
. Тогда  .
.
Можно находить обратную матрицу и методом Гаусса:



Таким образом, и здесь
 .
.
Мы видим, что эта матрица неотрицательна. Следовательно, матрица  продуктивна.
продуктивна.
Продолжим анализ продуктивности модели Леонтьева.
Пусть  – некоторое число. Известно, что бесконечная геометрическая прогрессия вида
– некоторое число. Известно, что бесконечная геометрическая прогрессия вида
 (8.4)
(8.4)
сходится при условии  , и её сумма равна
, и её сумма равна  . Убедимся, что аналогичное предложение имеет место при замене числа
. Убедимся, что аналогичное предложение имеет место при замене числа 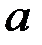 матрицей
матрицей  .
.
Лемма. Если бесконечный ряд
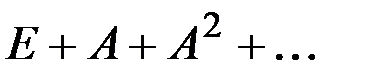 , (8.5)
, (8.5)
составленный из матриц, сходится, то его сумма есть матрица  .
.
Доказательство. Рассмотрим тождество
 . (8.6)
. (8.6)
Здесь  — частичная сумма ряда (8.5), а
— частичная сумма ряда (8.5), а  – общий член этого ряда. Поскольку по условию леммы ряд (8.5) сходится, то в силу необходимого признака сходимости ряда
– общий член этого ряда. Поскольку по условию леммы ряд (8.5) сходится, то в силу необходимого признака сходимости ряда
 , (8.7)
, (8.7)
а суммой ряда является предел последовательности частичных сумм  при неограниченном увеличении номера
при неограниченном увеличении номера  .
.
Прежде всего, покажем, что матрица  имеет обратную матрицу, то есть она невырожденная [7]. Рассуждая от противного, предположим, что она – вырожденная. По теореме 3.2 однородная система уравнений
имеет обратную матрицу, то есть она невырожденная [7]. Рассуждая от противного, предположим, что она – вырожденная. По теореме 3.2 однородная система уравнений
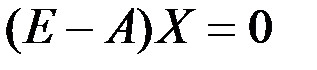 (8.8)
(8.8)
с вырожденной матрицей  обязательно имеет ненулевое решение
обязательно имеет ненулевое решение  . Домножим равенство (8.8) слева на матрицу
. Домножим равенство (8.8) слева на матрицу  . Тогда
. Тогда
 .
.
С учётом тождества (8.6) получим
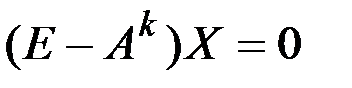
и перейдём к пределу при неограниченном увеличении номера  . Тогда
. Тогда

или, учитывая (8.7),
 ,
,
а значит  .
.
Полученное противоречие доказывает, что матрица  невырожденная и имеет обратную матрицу
невырожденная и имеет обратную матрицу  . Домножим (8.6) на матрицу
. Домножим (8.6) на матрицу  справа:
справа:
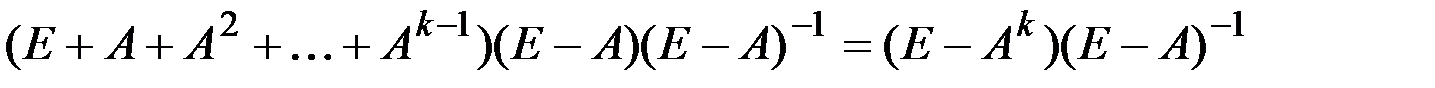 ,
,
и перейдём к пределу при неограниченном увеличении номера  .
.

Итак, поскольку предел последовательности частичных сумм равен  , то матрица
, то матрица  и есть сумма ряда (8.6), то есть
и есть сумма ряда (8.6), то есть
 . (8.9)
. (8.9)
Лемма доказана.
Третий критерий продуктивности. Матрица А ³0 продуктивна тогда и только тогда, когда сходиться бесконечный ряд (8.6):
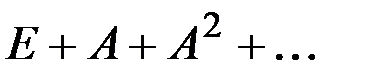
Доказательство следует из леммы и второго критерия продуктивности.
Следствие. Если продуктивна матрица  ,то продуктивна и продуктивна и матрица
,то продуктивна и продуктивна и матрица  .
.
Покажем, как третий критерий продуктивности может быть использован для проверки матрицы  на продуктивность. Например, если сумма элементов любого столбца матрицы A c неотрицательными элементами меньше 1, то А продуктивна. Заметим, что в стоимостной модели баланса это означает, что суммарный вклад всех отраслей в выпуск 1 руб. продукции конкретной отрасли меньше 1, то есть отрасль рентабельна.
на продуктивность. Например, если сумма элементов любого столбца матрицы A c неотрицательными элементами меньше 1, то А продуктивна. Заметим, что в стоимостной модели баланса это означает, что суммарный вклад всех отраслей в выпуск 1 руб. продукции конкретной отрасли меньше 1, то есть отрасль рентабельна.
Действительно, пусть  – наибольшая среди всех сумм
– наибольшая среди всех сумм  , и q <1. Ясно, что тогда все элементы матрицы А не превосходят q, то есть
, и q <1. Ясно, что тогда все элементы матрицы А не превосходят q, то есть  . Из правила перемножения матриц легко вывести, что любой элемент матрицы
. Из правила перемножения матриц легко вывести, что любой элемент матрицы  не превосходит
не превосходит  :
:
 .
.
Точно так же получим, что элементы матрицы А 3 не превосходит q 3 и т.д. Отсюда следует сходимость ряда (8.6), а значит, и продуктивность матрицы А.
Пример 8.2. Дана матрица
 .
.
Сумма элементов каждого столбца матрицы  меньше единицы. Следовательно, А продуктивна.
меньше единицы. Следовательно, А продуктивна.
В силу следствия третьего критерия продуктивности если в неотрицательной матрице  сумма элементов любой строки меньше 1, то матрица А продуктивна.
сумма элементов любой строки меньше 1, то матрица А продуктивна.
Запас продуктивности
Пусть  – продуктивная матрица. Запасом продуктивности матрицы
– продуктивная матрица. Запасом продуктивности матрицы  назовем такое число
назовем такое число  , что все матрицы
, что все матрицы  , где
, где  , продуктивны, а матрица
, продуктивны, а матрица 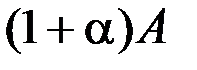 непродуктивна.
непродуктивна.
Пример 9.1. Выяснить, какой запас продуктивности имеет матрица
 .
.
Решение. В примере 8.1 было показано, что матрица  продуктивна. При нахождении запаса продуктивности будем руководствоваться вторым критерием продуктивности для матрицы
продуктивна. При нахождении запаса продуктивности будем руководствоваться вторым критерием продуктивности для матрицы  , где
, где  . Покажем существование неотрицательной матрицы
. Покажем существование неотрицательной матрицы  . В данном случае
. В данном случае
 . (9.1)
. (9.1)
Её обратная матрица имеет вид
 , (9.2)
, (9.2)
где  — определитель матрицы
— определитель матрицы  . Вычислим определитель
. Вычислим определитель  матрицы (9.1):
матрицы (9.1):
 .
.
Для продуктивности матрицы  нужно, чтобы все элементы обратной матрицы (9.2) были неотрицательными. Тогда:
нужно, чтобы все элементы обратной матрицы (9.2) были неотрицательными. Тогда:
 (9.3)
(9.3)
Решив совокупность неравенств (9.3), получим:
 .
.
Запас продуктивности матрицы  равен 0.08. Мы видим, что матрица
равен 0.08. Мы видим, что матрица  находится где-то «на пределе» продуктивности.
находится где-то «на пределе» продуктивности.
Обычно матрицы  межотраслевого баланса обладают большим запасом продуктивности. Рост производственных расходов вызывает увеличение элементов матрицы
межотраслевого баланса обладают большим запасом продуктивности. Рост производственных расходов вызывает увеличение элементов матрицы  и, как следствие, снижение ее запаса продуктивности.
и, как следствие, снижение ее запаса продуктивности.
Вектор полных затрат
Пусть задана матрица  с неотрицательными элементами, то есть
с неотрицательными элементами, то есть  . Равенство (8.6), доказанное в лемме пункта 2.8, вида
. Равенство (8.6), доказанное в лемме пункта 2.8, вида
 (10.1)
(10.1)
справедливо только том случае, когда матрица  продуктивна и имеет экономический смысл. Это значит, что модель Леонтьева (7.3) имеет решение вида (8.3):
продуктивна и имеет экономический смысл. Это значит, что модель Леонтьева (7.3) имеет решение вида (8.3):
 . (10.2)
. (10.2)
С учётом (10.1) это решение (10.3) может быть записано в виде
 . (10.3)
. (10.3)
Определим экономический смысл разложения вектора  на слагаемые
на слагаемые 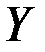 ,
,  ,
,  и т.д. Для получения валового выпуска
и т.д. Для получения валового выпуска  , обеспечивающего конечное потребление
, обеспечивающего конечное потребление  , нужно прежде всего произвести набор товаров, описываемый вектором
, нужно прежде всего произвести набор товаров, описываемый вектором  . Но этого мало, ведь для получения
. Но этого мало, ведь для получения  нужно затратить (а значит, сначала произвести) продукцию, описываемую вектором
нужно затратить (а значит, сначала произвести) продукцию, описываемую вектором  . Но и этого мало: для получения
. Но и этого мало: для получения  нужно осуществить дополнительные затраты, описываемые вектором
нужно осуществить дополнительные затраты, описываемые вектором  . В итоге приходим к заключению, что весь валовой выпуск
. В итоге приходим к заключению, что весь валовой выпуск  должен составляться из слагаемых
должен составляться из слагаемых 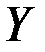 ,
,  ,
,  и т.д. Именно это и зафиксировано в формуле (10.3). В соответствии с этим рассуждением сумму
и т.д. Именно это и зафиксировано в формуле (10.3). В соответствии с этим рассуждением сумму

называют вектором полных затрат, а сделанное выше заключение формулируют так: вектор валового выпуска  совпадает с вектором полных затрат.
совпадает с вектором полных затрат.
Чтобы сделать заключение более конкретным, рассмотрим пример. Пусть речь идет о блоке из трех промышленных отраслей:
· строительные материалы;
· производство электроэнергии;
· строительная техника.
Для получения конечного выпуска  необходимо, прежде всего, произвести:
необходимо, прежде всего, произвести:
 строительных материалов;
строительных материалов;
 электроэнергии;
электроэнергии;
 строительной техники.
строительной техники.
Но для производства  строительных материалов необходимо затратить (а значит, сначала произвести) какие-то количества сырья, электроэнергии и техники. То же самое справедливо и в отношении производства
строительных материалов необходимо затратить (а значит, сначала произвести) какие-то количества сырья, электроэнергии и техники. То же самое справедливо и в отношении производства  электроэнергии и
электроэнергии и  техники.
техники.
Таким образом, искомый валовой выпуск  представляет собой сумму затрат 0-го порядка (вектор
представляет собой сумму затрат 0-го порядка (вектор 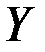 ), 1-го порядка (вектор
), 1-го порядка (вектор  ), 2-го порядка (вектор
), 2-го порядка (вектор  ) и т.д.
) и т.д.
Модель равновесных цен
Рассмотрим теперь балансовую модель, двойственную модели Леонтьева – так называемую модель равновесных цен. Пусть, как и прежде,  – матрица прямых затрат,
– матрица прямых затрат,  – вектор валового выпуска. Обозначим через
– вектор валового выпуска. Обозначим через 
 вектор цен,
вектор цен,  -ая координата которого равна цене единицы продукции
-ая координата которого равна цене единицы продукции  -й отрасли. Тогда, например, первая отрасль получит доход, равный
-й отрасли. Тогда, например, первая отрасль получит доход, равный  ., а
., а  -ая отрасль – доход, равный
-ая отрасль – доход, равный 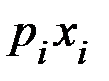 . Часть своего дохода
. Часть своего дохода  -тая отрасль потратит на закупку продукции у других отраслей. Так, для выпуска единицы продукции, ей необходима продукция первой отрасли в объеме
-тая отрасль потратит на закупку продукции у других отраслей. Так, для выпуска единицы продукции, ей необходима продукция первой отрасли в объеме 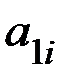 , второй отрасли в объеме
, второй отрасли в объеме  , и т.д.,
, и т.д.,  -ой отрасли в объеме
-ой отрасли в объеме  . На покупку этой продукции ею будет затрачена сумма, равная
. На покупку этой продукции ею будет затрачена сумма, равная  . Следовательно, для выпуска продукции в объеме
. Следовательно, для выпуска продукции в объеме 
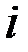 -ой отрасли необходимо потратить на закупку продукции других отраслей сумму, равную
-ой отрасли необходимо потратить на закупку продукции других отраслей сумму, равную  . Оставшуюся часть дохода, называемую добавленной стоимостью, мы обозначим через
. Оставшуюся часть дохода, называемую добавленной стоимостью, мы обозначим через  (эта часть дохода идет на выплату зарплаты и налогов, предпринимательскую прибыль и инвестиции).
(эта часть дохода идет на выплату зарплаты и налогов, предпринимательскую прибыль и инвестиции).
Таким образом, имеет место следующее равенство:
 .
.
Разделив это равенство на  , получим:
, получим:
 ,
,
где  – норма добавленной стоимости (величина добавленной стоимости на единицу выпускаемой продукции).
– норма добавленной стоимости (величина добавленной стоимости на единицу выпускаемой продукции).
Тогда получаем совокупность равенств:
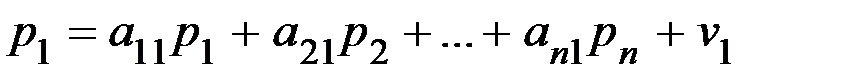 ;
;

 .
.
Найденные равенства могут быть записаны в матричной форме следующим образом:
 , (11.1)
, (11.1)
где  ,
,  ,
,  – матрица прямых затрат. Вектор
– матрица прямых затрат. Вектор 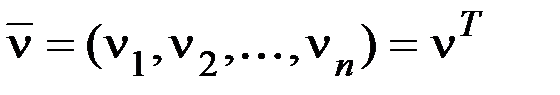 называют вектором норм добавленной стоимости. Сравнивая (11.1) с моделью Леонтьева (7.3), мы видим, что полученные уравнения очень похожи. Если в уравнении Леонтьева (7.3) вектор
называют вектором норм добавленной стоимости. Сравнивая (11.1) с моделью Леонтьева (7.3), мы видим, что полученные уравнения очень похожи. Если в уравнении Леонтьева (7.3) вектор  заменить вектором
заменить вектором  , вектор
, вектор  – вектором
– вектором  , а матрицу
, а матрицу  – на
– на  , то получим уравнение (11.1).
, то получим уравнение (11.1).
Модель равновесных цен позволяет, зная величины норм добавленной стоимости, прогнозировать цены на продукцию отраслей, а также изменение цен и инфляцию, являющиеся следствием изменения цены в одной из отраслей.
Пример 11.1. Рассмотрим экономическую систему, состоящую из трех отраслей: строительные материалы; энергопотребление; строительная техника.
Пусть

– транспонированная матрица прямых затрат,  – вектор норм добавленной стоимости.
– вектор норм добавленной стоимости.
Определим равновесные цены. Для этого, как и в модели Леонтьева воспользуемся формулой
 .
.
Выпишем матрицу

и вычислим её определитель
 .
.
После необходимых вычислений имеем
 .
.
Тогда:

Допустим, что в отрасли, изготавливающей строительные материалы, произойдет увеличение нормы добавленной стоимости на 0,3. Определим равновесные цены в этом случае. Поскольку вектор норм добавленной стоимости  , то
, то


Определив равновесные цены в этом случае, находим, что продукция отраслей подорожала на 2,7%, 0,4%, 0,8% соответственно. Зная объемы выпуска, можно подсчитать вызванную инфляцию.
ВАРИАНТЫ ИНДИВИДУАЛЬНОГО ДОМАШНЕГО ЗАДАНИЯ
Варианты индивидуального домашнего задания предназначенного для самостоятельного выполнения.
Задание 1 выполняется по формулам (1.1), (1.2), (1.5) и (1.6) пункта 2.1.
Задание 2 разобрано в примере 8.4 пункта 1.8 первого раздела.
Задание 3 разобрано в примере 4.1 пункта 2.4 второго раздела.
Задание 4 разобрано в примере 6.6 пункта 2.6 второго раздела.
В задании 5 применяется Критерий Сильвестра, который разобран в примерах 6.7 – 6.9 пункта 2.6 второго раздела.
Вариант 1
1. Найти нормы и скалярное произведение векторов  и
и  , если
, если  ;
;  . Найти координаты вектора
. Найти координаты вектора  .
.
2. Найти ранг матрицы

с помощью элементарных преобразований.
3. Найти собственные значения и собственные векторы матрицы
 , если
, если
а)  ; б)
; б)  .
.
4. Найти матрицу квадратичной формы

Методом выделения полных квадратов привести  к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы.
5. Дана симметрическая матрица
 .
.
Составить соответствующую ей квадратичную форму 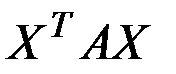 и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра.
Вариант 2
1. Найти нормы и скалярное произведение векторов  и
и  , если
, если  ;
; 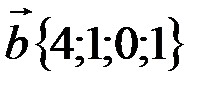 . Найти координаты вектора
. Найти координаты вектора 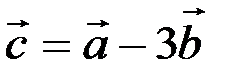 .
.
2. Найти ранг матрицы

с помощью элементарных преобразований.
3. Найти собственные значения и собственные векторы матрицы
 , если
, если
а)  ; б)
; б)  .
.
4. Найти матрицу квадратичной формы
 .
.
Методом выделения полных квадратов привести  к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы.
5. Дана симметрическая матрица
 .
.
Составить соответствующую ей квадратичную форму 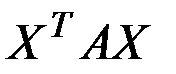 и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра.
Вариант 3
1. Найти нормы и скалярное произведение векторов  и
и  , если
, если  ;
; 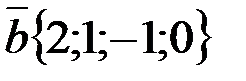 . Найти координаты вектора
. Найти координаты вектора  .
.
2. Найти ранг матрицы

с помощью элементарных преобразований.
3. Найти собственные значения и собственные векторы матрицы  , если
, если
а)  ; б)
; б)  .
.
4. Найти матрицу квадратичной формы

Методом выделения полных квадратов привести  к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы.
5. Дана симметрическая матрица
 .
.
Составить соответствующую ей квадратичную форму 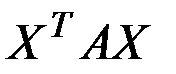 и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра.
Вариант 4
1. Найти нормы и скалярное произведение векторов  и
и 
 ;
; 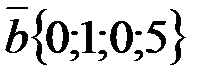 . Найти координаты вектора
. Найти координаты вектора  .
.
2. Найти ранг матрицы с помощью элементарных преобразований
 .
.
3. Найти собственные значения и собственные векторы матрицы 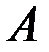 , если
, если
а)  ; б)
; б)  .
.
4. Найти матрицу квадратичной формы

Выделением полных квадратов привести  к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы.
5. Дана симметрическая матрица
 .
.
Составить соответствующую ей квадратичную форму  и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра.
Вариант 5
1. Найти нормы и скалярное произведение векторов  и
и 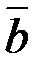 , если
, если
 ;
;  . Найти координаты вектора
. Найти координаты вектора  .
.
2. Найти ранг матрицы с помощью элементарных преобразований
 .
.
3. Найти собственные значения и собственные векторы матрицы 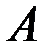 , если
, если
а)  ; б)
; б)  .
.
4. Найти матрицу квадратичной формы
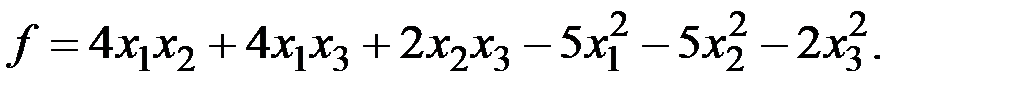
Методом выделения полных квадратов привести  к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы.
5. Дана симметрическая матрица
 .
.
Составить соответствующую ей квадратичную форму  и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра.
Вариант 6
1. Найти нормы и скалярное произведение векторов  и
и  , если
, если
 ;
;  . Найти координаты вектора
. Найти координаты вектора  .
.
2. Найти ранг матрицы с помощью элементарных преобразований
 .
.
3. Найти собственные значения и собственные векторы матрицы 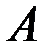 , если
, если
а)  ; б)
; б)  .
.
4. Найти матрицу квадратичной формы

Методом выделения полных квадратов привести  к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы.
5. Дана симметрическая матрица
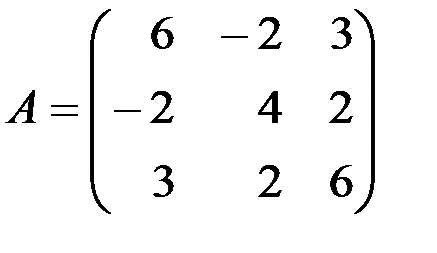 .
.
Составить соответствующую ей квадратичную форму  и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра.
Вариант 7
1. Найти нормы и скалярное произведение векторов  и
и  , если
, если
 ;
;  . Найти координаты вектора
. Найти координаты вектора  .
.
2. Найти ранг матрицы с помощью элементарных преобразований
 .
.
3. Найти собственные значения и собственные векторы матрицы  , если
, если
а)  ; б)
; б)  .
.
4. Найти матрицу квадратичной формы

Методом выделения полных квадратов привести  к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы.
5. Дана симметрическая матрица
 .
.
Составить соответствующую ей квадратичную форму  и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра.
Вариант 8
1. Найти нормы и скалярное произведение векторов  и
и 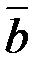 , если
, если  ;
;  .Найти координаты вектора
.Найти координаты вектора  .
.
2. Найти ранг матрицы с помощью элементарных преобразований
 .
.
3. Найти собственные значения и собственные векторы матрицы 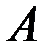 , если
, если
а) 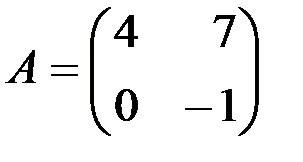 ; б)
; б)  .
.
4. Найти матрицу квадратичной формы

Методом выделения полных квадратов привести  к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы.
5. Дана симметрическая матрица
 .
.
Составить соответствующую ей квадратичную форму  и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра.
Вариант 9
1. Найти нормы и скалярное произведение векторов  и
и  , если
, если
 ;
;  . Найти координаты вектора
. Найти координаты вектора 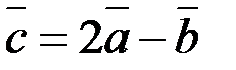 .
.
2. Найти ранг матрицы с помощью элементарных преобразований
 .
.
3. Найти собственные значения и собственные векторы матрицы  , если
, если
а)  ; б)
; б)  .
.
4. Найти матрицу квадратичной формы
 .
.
Методом выделения полных квадратов привести 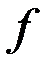 к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы.
5. Дана симметрическая матрица
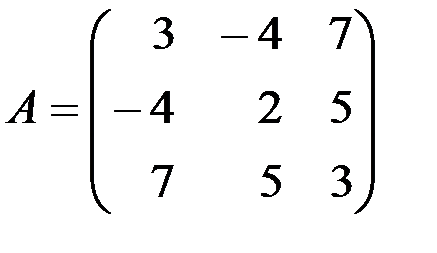 .
.
Составить соответствующую ей квадратичную форму  и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра.
Вариант 10
1. Найти нормы и скалярное произведение векторов  и
и  , если
, если
 ;
;  . Найти координаты вектора
. Найти координаты вектора  .
.
2. Найти ранг матрицы с помощью элементарных преобразований
 .
.
3. Найти собственные значения и собственные векторы матрицы 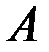 , если
, если
а)  ; б)
; б) 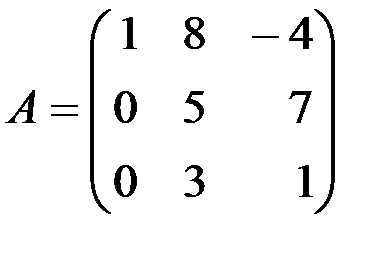 .
.
4. Найти матрицу квадратичной формы

Методом выделения полных квадратов привести  к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы.
5. Дана симметрическая матрица
 .
.
Составить соответствующую ей квадратичную форму  и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра.
Вариант 11
1. Найти нормы и скалярное произведение векторов  и
и 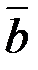 , если
, если  ;
; 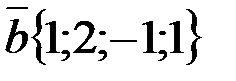 . Найти координаты вектора
. Найти координаты вектора  .
.
2. Найти ранг матрицы с помощью элементарных преобразований
 .
.
3. Найти собственные значения и собственные векторы матрицы  , если
, если
а) 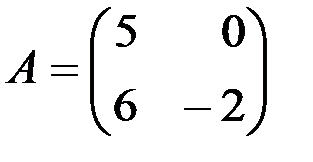 ; б)
; б)  .
.
4. Найти матрицу квадратичной формы

Методом выделения полных квадратов привести  к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы.
5. Дана симметрическая матрица
 .
.
Составить соответствующую ей квадратичную форму  и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра.
Вариант 12
1. Найти нормы и скалярное произведение векторов 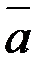 и
и  , если
, если
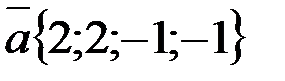 ;
;  . Найти координаты вектора
. Найти координаты вектора  .
.
2. Найти ранг матрицы с помощью элементарных преобразований
 .
.
3. Найти собственные значения и собственные векторы матрицы  , если
, если
а)  ; б)
; б)  .
.
4. Найти матрицу квадратичной формы

Методом выделением полных квадратов привести 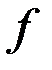 к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы.
5. Дана симметрическая матрица
 .
.
Составить соответствующую ей квадратичную форму  и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра.
Вариант 13
1. Найти нормы и скалярное произведение векторов 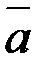 и
и  , если
, если 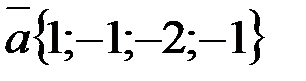 ;
;  .Найти координаты вектора
.Найти координаты вектора 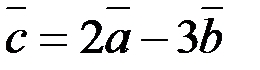 .
.
2. Найти ранг матрицы с помощью элементарных преобразований

|
|
|



 с неотрицательными компонентами называется продуктивной, если для любого
с неотрицательными компонентами называется продуктивной, если для любого 
 существует неотрицательное решение
существует неотрицательное решение 
 уравнения
уравнения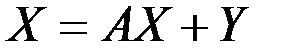 . (8.1)
. (8.1)
 конечного потребления можно получить при подходящем валовом выпуске
конечного потребления можно получить при подходящем валовом выпуске 
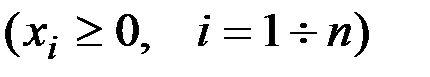 .
. уравнения (8.1) для любого вектора
уравнения (8.1) для любого вектора 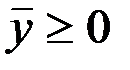 . Достаточно, чтобы такое решение существовало хотя бы для одного вектора
. Достаточно, чтобы такое решение существовало хотя бы для одного вектора  . Условимся в дальнейшем называть вектор
. Условимся в дальнейшем называть вектор  положительным, если все компоненты этого вектора строго положительны.
положительным, если все компоненты этого вектора строго положительны. и для некоторого положительного вектора
и для некоторого положительного вектора  уравнение (8.1) имеет неотрицательное решение
уравнение (8.1) имеет неотрицательное решение 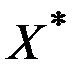 , где
, где  , то матрица
, то матрица  продуктивна.
продуктивна. . Это следует из уравнения (8.1)
. Это следует из уравнения (8.1)  и
и 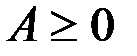 ,
,  ,
,  .
. , (8.2)
, (8.2) – единичная матрица. Будем искать матрицу, обратную по отношению к матрице
– единичная матрица. Будем искать матрицу, обратную по отношению к матрице  .
.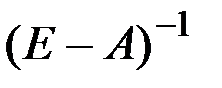 существует, то из уравнения (8.2) следует, что
существует, то из уравнения (8.2) следует, что . (8.3)
. (8.3)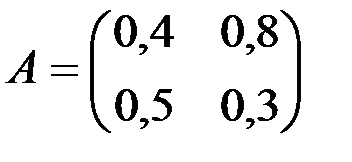 .
. .
.
 имеет вид
имеет вид  . Тогда
. Тогда  .
.


 .
. продуктивна.
продуктивна. – некоторое число. Известно, что бесконечная геометрическая прогрессия вида
– некоторое число. Известно, что бесконечная геометрическая прогрессия вида (8.4)
(8.4) , и её сумма равна
, и её сумма равна  . Убедимся, что аналогичное предложение имеет место при замене числа
. Убедимся, что аналогичное предложение имеет место при замене числа 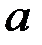 матрицей
матрицей  .
.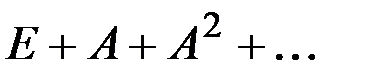 , (8.5)
, (8.5) .
. . (8.6)
. (8.6) — частичная сумма ряда (8.5), а
— частичная сумма ряда (8.5), а  – общий член этого ряда. Поскольку по условию леммы ряд (8.5) сходится, то в силу необходимого признака сходимости ряда
– общий член этого ряда. Поскольку по условию леммы ряд (8.5) сходится, то в силу необходимого признака сходимости ряда , (8.7)
, (8.7) .
. имеет обратную матрицу, то есть она невырожденная [7]. Рассуждая от противного, предположим, что она – вырожденная. По теореме 3.2 однородная система уравнений
имеет обратную матрицу, то есть она невырожденная [7]. Рассуждая от противного, предположим, что она – вырожденная. По теореме 3.2 однородная система уравнений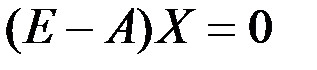 (8.8)
(8.8) обязательно имеет ненулевое решение
обязательно имеет ненулевое решение  .
.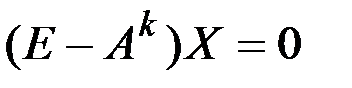
 . Тогда
. Тогда
 ,
, .
.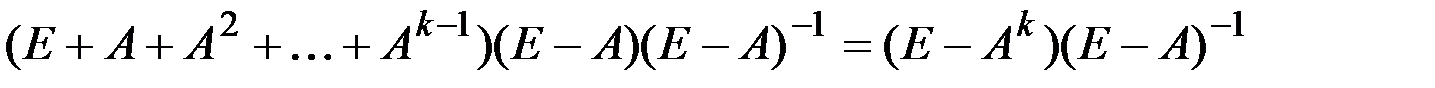 ,
,
 . (8.9)
. (8.9) ,то продуктивна и продуктивна и матрица
,то продуктивна и продуктивна и матрица  .
. на продуктивность. Например, если сумма элементов любого столбца матрицы A c неотрицательными элементами меньше 1, то А продуктивна. Заметим, что в стоимостной модели баланса это означает, что суммарный вклад всех отраслей в выпуск 1 руб. продукции конкретной отрасли меньше 1, то есть отрасль рентабельна.
на продуктивность. Например, если сумма элементов любого столбца матрицы A c неотрицательными элементами меньше 1, то А продуктивна. Заметим, что в стоимостной модели баланса это означает, что суммарный вклад всех отраслей в выпуск 1 руб. продукции конкретной отрасли меньше 1, то есть отрасль рентабельна. – наибольшая среди всех сумм
– наибольшая среди всех сумм  , и q <1. Ясно, что тогда все элементы матрицы А не превосходят q, то есть
, и q <1. Ясно, что тогда все элементы матрицы А не превосходят q, то есть  . Из правила перемножения матриц легко вывести, что любой элемент матрицы
. Из правила перемножения матриц легко вывести, что любой элемент матрицы  не превосходит
не превосходит  :
: .
. .
. меньше единицы. Следовательно, А продуктивна.
меньше единицы. Следовательно, А продуктивна. сумма элементов любой строки меньше 1, то матрица А продуктивна.
сумма элементов любой строки меньше 1, то матрица А продуктивна. – продуктивная матрица. Запасом продуктивности матрицы
– продуктивная матрица. Запасом продуктивности матрицы 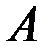 назовем такое число
назовем такое число  , что все матрицы
, что все матрицы  , где
, где  , продуктивны, а матрица
, продуктивны, а матрица 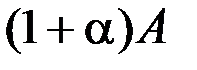 непродуктивна.
непродуктивна. .
. продуктивна. При нахождении запаса продуктивности будем руководствоваться вторым критерием продуктивности для матрицы
продуктивна. При нахождении запаса продуктивности будем руководствоваться вторым критерием продуктивности для матрицы  , где
, где  . Покажем существование неотрицательной матрицы
. Покажем существование неотрицательной матрицы  . В данном случае
. В данном случае . (9.1)
. (9.1) , (9.2)
, (9.2) — определитель матрицы
— определитель матрицы  . Вычислим определитель
. Вычислим определитель  .
. нужно, чтобы все элементы обратной матрицы (9.2) были неотрицательными. Тогда:
нужно, чтобы все элементы обратной матрицы (9.2) были неотрицательными. Тогда: (9.3)
(9.3) .
. равен 0.08. Мы видим, что матрица
равен 0.08. Мы видим, что матрица  находится где-то «на пределе» продуктивности.
находится где-то «на пределе» продуктивности. с неотрицательными элементами, то есть
с неотрицательными элементами, то есть  . Равенство (8.6), доказанное в лемме пункта 2.8, вида
. Равенство (8.6), доказанное в лемме пункта 2.8, вида (10.1)
(10.1) продуктивна и имеет экономический смысл. Это значит, что модель Леонтьева (7.3) имеет решение вида (8.3):
продуктивна и имеет экономический смысл. Это значит, что модель Леонтьева (7.3) имеет решение вида (8.3): . (10.3)
. (10.3) на слагаемые
на слагаемые 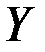 ,
,  ,
,  и т.д. Для получения валового выпуска
и т.д. Для получения валового выпуска  , обеспечивающего конечное потребление
, обеспечивающего конечное потребление  , нужно прежде всего произвести набор товаров, описываемый вектором
, нужно прежде всего произвести набор товаров, описываемый вектором  . Но этого мало, ведь для получения
. Но этого мало, ведь для получения  нужно затратить (а значит, сначала произвести) продукцию, описываемую вектором
нужно затратить (а значит, сначала произвести) продукцию, описываемую вектором  . В итоге приходим к заключению, что весь валовой выпуск
. В итоге приходим к заключению, что весь валовой выпуск 
 необходимо, прежде всего, произвести:
необходимо, прежде всего, произвести: строительных материалов;
строительных материалов; электроэнергии;
электроэнергии; строительной техники.
строительной техники. – матрица прямых затрат,
– матрица прямых затрат, 
 вектор цен,
вектор цен,  -ая координата которого равна цене единицы продукции
-ая координата которого равна цене единицы продукции  -й отрасли. Тогда, например, первая отрасль получит доход, равный
-й отрасли. Тогда, например, первая отрасль получит доход, равный  ., а
., а  -ая отрасль – доход, равный
-ая отрасль – доход, равный 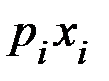 . Часть своего дохода
. Часть своего дохода  -тая отрасль потратит на закупку продукции у других отраслей. Так, для выпуска единицы продукции, ей необходима продукция первой отрасли в объеме
-тая отрасль потратит на закупку продукции у других отраслей. Так, для выпуска единицы продукции, ей необходима продукция первой отрасли в объеме 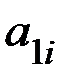 , второй отрасли в объеме
, второй отрасли в объеме  , и т.д.,
, и т.д.,  -ой отрасли в объеме
-ой отрасли в объеме  . На покупку этой продукции ею будет затрачена сумма, равная
. На покупку этой продукции ею будет затрачена сумма, равная  . Следовательно, для выпуска продукции в объеме
. Следовательно, для выпуска продукции в объеме 
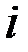 -ой отрасли необходимо потратить на закупку продукции других отраслей сумму, равную
-ой отрасли необходимо потратить на закупку продукции других отраслей сумму, равную  . Оставшуюся часть дохода, называемую добавленной стоимостью, мы обозначим через
. Оставшуюся часть дохода, называемую добавленной стоимостью, мы обозначим через  (эта часть дохода идет на выплату зарплаты и налогов, предпринимательскую прибыль и инвестиции).
(эта часть дохода идет на выплату зарплаты и налогов, предпринимательскую прибыль и инвестиции). .
. , получим:
, получим: ,
, – норма добавленной стоимости (величина добавленной стоимости на единицу выпускаемой продукции).
– норма добавленной стоимости (величина добавленной стоимости на единицу выпускаемой продукции).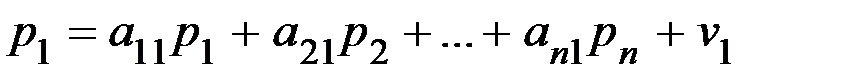 ;
;
 .
. , (11.1)
, (11.1) ,
,  ,
,  – матрица прямых затрат. Вектор
– матрица прямых затрат. Вектор 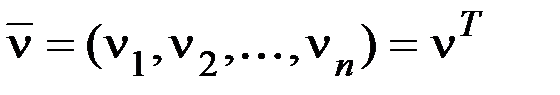 называют вектором норм добавленной стоимости. Сравнивая (11.1) с моделью Леонтьева (7.3), мы видим, что полученные уравнения очень похожи. Если в уравнении Леонтьева (7.3) вектор
называют вектором норм добавленной стоимости. Сравнивая (11.1) с моделью Леонтьева (7.3), мы видим, что полученные уравнения очень похожи. Если в уравнении Леонтьева (7.3) вектор  заменить вектором
заменить вектором  , вектор
, вектор  – вектором
– вектором  , а матрицу
, а матрицу  – на
– на  , то получим уравнение (11.1).
, то получим уравнение (11.1).
 – вектор норм добавленной стоимости.
– вектор норм добавленной стоимости. .
.
 .
. .
.
 , то
, то
 и
и  , если
, если  ;
;  . Найти координаты вектора
. Найти координаты вектора  .
.
 , если
, если ; б)
; б)  .
.
 к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы. .
.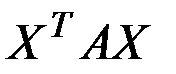 и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра. ;
; 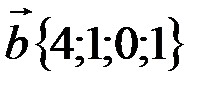 . Найти координаты вектора
. Найти координаты вектора 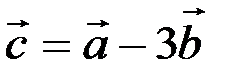 .
.
 , если
, если ; б)
; б)  .
. .
. .
. и
и  , если
, если  ;
; 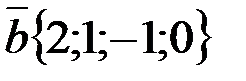 . Найти координаты вектора
. Найти координаты вектора  .
.
 , если
, если ; б)
; б)  .
.
 к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы. .
. и
и 
 ;
; 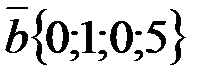 . Найти координаты вектора
. Найти координаты вектора  .
. .
. , если
, если ; б)
; б)  .
.
 к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы. .
. и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра. и
и  , если
, если ;
;  . Найти координаты вектора
. Найти координаты вектора  .
. .
. , если
, если ; б)
; б)  .
.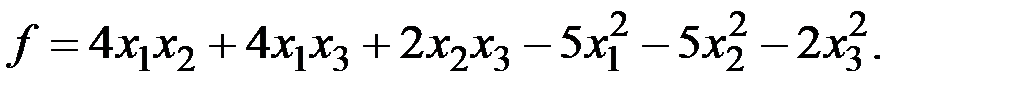
 к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы. .
. и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра. и
и  , если
, если ;
;  . Найти координаты вектора
. Найти координаты вектора  .
. .
. ; б)
; б)  .
.
 к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы.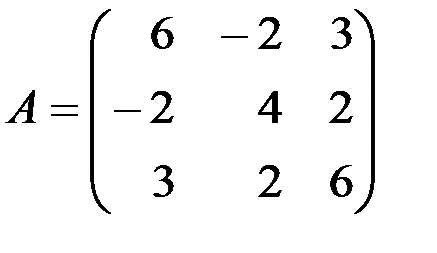 .
. и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра. и
и  , если
, если ;
;  . Найти координаты вектора
. Найти координаты вектора  .
. .
. , если
, если ; б)
; б)  .
.
 к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы. .
. и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра. и
и 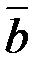 , если
, если  ;
;  .Найти координаты вектора
.Найти координаты вектора  .
. .
.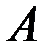 , если
, если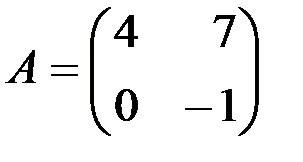 ; б)
; б)  .
.
 к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы. .
. и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра. и
и  , если
, если ;
;  . Найти координаты вектора
. Найти координаты вектора 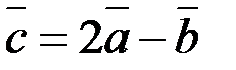 .
. .
. , если
, если ; б)
; б)  .
. .
.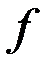 к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы.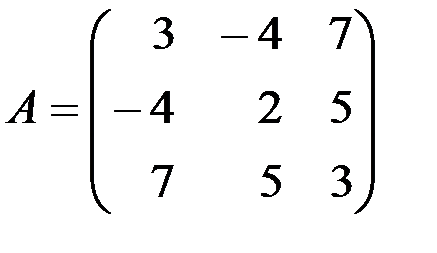 .
. и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра. и
и  , если
, если ;
;  . Найти координаты вектора
. Найти координаты вектора  .
. .
.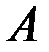 , если
, если ; б)
; б) 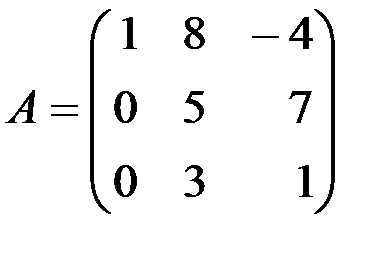 .
.
 к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы. .
. и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра. и
и 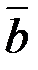 , если
, если  ;
; 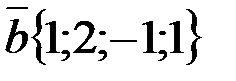 . Найти координаты вектора
. Найти координаты вектора  .
. .
. , если
, если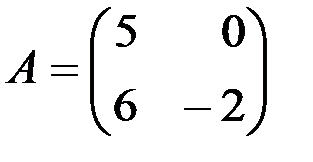 ; б)
; б)  .
.
 к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы. .
. и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра.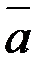 и
и  , если
, если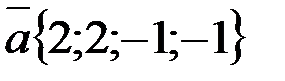 ;
;  . Найти координаты вектора
. Найти координаты вектора  .
. .
. , если
, если ; б)
; б)  .
.
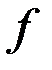 к сумме квадратов и определить тип формы.
к сумме квадратов и определить тип формы. .
. и определить тип формы с помощью критерия Сильвестра.
и определить тип формы с помощью критерия Сильвестра.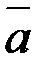 и
и  , если
, если 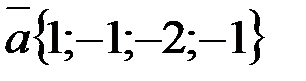 ;
;  .Найти координаты вектора
.Найти координаты вектора 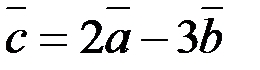 .
.


