Знать:
v Основные тригонометрические формулы;
v основные приёмы интегрирования тригонометрических выражений.
Уметь:
v Использовать основные приёмы интегрирования тригонометрических выражений.
Использование тригонометрических преобразований
Интегралы вида:
 ;
;  ;
;  , (16)
, (16)
где  , находятся с помощью формул:
, находятся с помощью формул:
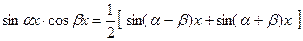 ;
;
 ;
;
 .
.
Интегралы вида:
 , (17)
, (17)
Данный интеграл сводится к интегралу от рациональной дроби при помощи универсальной тригонометрической подстановки
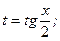



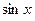 =
=  ;
;  .
.
На практике применяются и другие, более простые подстановки, в зависимости от свойств (и вида) подынтегральной функции.
- если функция R (sin x;cos x) нечётна относительно sin x, т.е. R (-sin x;cos x)=- R (sin x; cos x), то следует применить подстановку
t =cos x; dt = -sin xdx;  ,
, 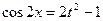 .
.
- если функция R (sin x;cos x) нечётна относительно cos x, т.е. R (sin x;-cos x)=- R (sin x; cos x), то следует применить подстановку
t =sin x; dt =cos x dx;  .
.
- если функция R (sin x;cos x) чётна относительно sin x и cos x, т.е. R (-sin x;-cos x)= R (sin x;cos x), то следует применить подстановку
t =tg x;  ;
;
 ,
,  .
.
Интегралы вида:
 , (18)
, (18)
1. где k, n — хотя бы одно число нечётное
отделить от нечётной степени один множитель и подвести его под знак дифференциала;
2. где k, n — чётные положительные
применить формулы понижения степени:
 ;
;  ;
;  ;
;
3. где k, n — нечётные положительные
отделить от наименьшей степени один множитель и подвести его под знак дифференциала;
4. где n — целое положительное число
применить подстановку t =sin x;
5. где k — целое положительное нечётное число
применить подстановку t =cos x;
6. где n+k — чётное отрицательное целое число
применить подстановку t =tg x;
7. где n и k — четные и хотя бы одно из них отрицательное
применить подстановку t = tg x или t = ctg x.
Интегралы вида:
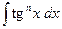 ,
,  ,
, 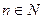 (19)
(19)
если n =1, то
 ;
;
 ,
,
если n >1, воспользоваться формулами:
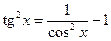 ;
;  ,
,
позволяющими понизить степень тангенса или котангенса непосредственно, отделяем один множитель и подводим его под знак дифференциала, находим исходный интеграл.
№6. Найти интегралы: 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5) 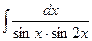 ;
;
6)  .
.
►1)  =
= 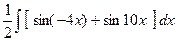 =
=
=  =
=  ;
;
2)  =
= 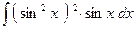 =
=  =
=
=  =
=
=  =
=
=  ;
;
3)  =
= 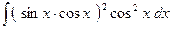 =
=
=  =
=  =
=
=  =
=  =
=
=  ;
;
4)  =
=  =
=  =
=
= 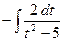 =
=  =
=  ;
;
5) 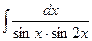 =
=  =
=  =
=
=  =
=  =
=  =
=
=  =
=  =
=  =
=
=  +С;
+С;
6)  =
=  =
=  =
= 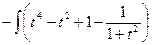 =
=
=  =
= 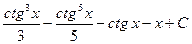 , (
, ( .◄
.◄
Аудиторное занятие
Найти интегралы:
№248. 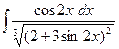 . Ответ:
. Ответ:  .
.
№249.  . Ответ:
. Ответ:  .
.
№250.  . Ответ:
. Ответ:  .
.
№251.  . Ответ:
. Ответ:  .
.
№252.  . Ответ:
. Ответ:  .
.
№253. 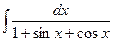 . Ответ:
. Ответ:  .
.
№254.  . Ответ:
. Ответ:  .
.
№255.  . Ответ:
. Ответ:  .
.
№256.  . Ответ:
. Ответ:  .
.
№257.  . Ответ:
. Ответ:  .
.
№258.  . Ответ:
. Ответ:  .
.
№259.  . Ответ:
. Ответ:  .
.
№260.  .
.
Указание. Замена сos x =t.
Ответ:  .
.
№261.  .
.
Указание. Замена sin x = t.
Ответ:  .
.
Домашнее задание
Найти интегралы:
№262.  . Ответ:
. Ответ:  .
.
№263.  . Ответ:
. Ответ: 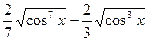 .
.
№264.  . Ответ:
. Ответ:  .
.
№265. 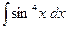 . Ответ:
. Ответ: 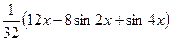 .
.
№266.  . Ответ:
. Ответ:  .
.
№267.  . Ответ: tg x – x.
. Ответ: tg x – x.
№268.  . Ответ:
. Ответ:  .
.
№269.  . Ответ:
. Ответ:  .
.
№270. 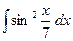 . Ответ:
. Ответ:  .
.
№271.  . Ответ:
. Ответ:  .
.
№272.  . Ответ:
. Ответ:  .
.
№273.  . Ответ:
. Ответ:  .
.
№274.  . Ответ:
. Ответ:  .
.
№275.  . Ответ:
. Ответ:  .
.
№276.  . Ответ:
. Ответ:  .
.
№277. 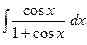 . Ответ:
. Ответ:  .
.
№278.  . Ответ:
. Ответ: 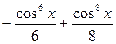 .
.
№279.  . Ответ:
. Ответ:  .
.
№280.  . Ответ:
. Ответ:  .
.
Дополнительные задания
Найти интегралы:
№281. 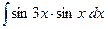 . Ответ:
. Ответ:  .
.
№282.  . Ответ:
. Ответ:  .
.
№283.  . Ответ:
. Ответ:  .
.
№284.  .
.
Ответ:  .
.
№285. 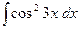 . Ответ:
. Ответ:  .
.
№286.  .
.
Ответ:  .
.
№287.  .
.
Ответ:  .
.
№288.  . Ответ:
. Ответ:  .
.
№289. 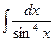 .
.
Указание. Замена t =ctg x. Ответ: 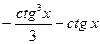 .
.
№290.  . Ответ:
. Ответ: 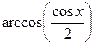 .
.
№291.  . Ответ:
. Ответ:  .
.
№292.  . Ответ:
. Ответ:  , где t =tg x.
, где t =tg x.
№293.  . Ответ: ln|tg x |.
. Ответ: ln|tg x |.
№294. 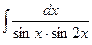 . Ответ:
. Ответ:  .
.
№295.  .
.
Указание. Замена ctg x = t.
Ответ:  .
.
№296.  . Ответ: ln|sin x |-sin x.
. Ответ: ln|sin x |-sin x.
№297.  .
.
Ответ:  .
.
Примерный вариан решения
индивидуального домашнего задания
Найти интегралы:
№18.  .
.
►  =
=  =
=
=  =
=
= 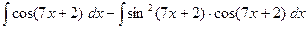 =
=
=  .◄
.◄
№19. 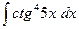 .
.
► 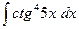 =
=  =
=
=  =
=  =
=
=  . ◄
. ◄
№20.  .
.
►  =
=  =
=
= 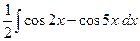 =
=  .◄
.◄
№38. 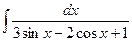 .
.
► 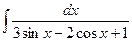 =
=  =
=
=  =
=  =
=  =
=
=  .◄
.◄
№39.  .
.
►  =
=  =
=
= 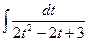 =
=  =
=  =
=
=  .◄
.◄
№40. 
►  =
=  =
=
=  =
=  =
= 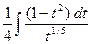 =
=
=  =
=  =
=
= 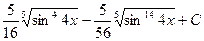 .◄
.◄
Занятие 7
Интегрирование некоторых иррациональностей
Цели
Знать:
v Основные приёмы интегрирования квадратичных иррациональностей.
Уметь:
v Применять основные приёмы интегрирования квадратичных иррациональностей;
v выделять полный квадрат из квадратного трёхчлена под знаком радикала;
v применять дробно-линейную подстановку; тригонометрическую подстановку.
Интегралы вида:
 (20)
(20)
называют неопределёнными интегралами от квадратичных иррациональностей.
Постановка задачи. Найти интеграл  .
.
План решения.
Для нахождения интеграла следует:
1. Если числитель есть дифференциал подкоренного трёхчлена, то следует сделать замену  , что приводит исходный интеграл к виду
, что приводит исходный интеграл к виду  .
.
2. Если числитель не зависит от х, т.е. М =0, то под знаком радикала выделим полный квадрат из квадратного трёхчлена, в результате чего получим квадратный двучлен, в зависимости от знака а исходный интеграл сводится к одной из табличных формул
 [11]
[11]
или
 [12].
[12].
3. Если  , то под знаком радикала выделив полный квадрат, сделать подстановку
, то под знаком радикала выделив полный квадрат, сделать подстановку  , при этом исходный интеграл разбивается на сумму двух интегралов.
, при этом исходный интеграл разбивается на сумму двух интегралов.
Интегралы вида
 , (21)
, (21)
где R — рациональная функция; p, q,…, s, t — целые числа, находятся с помощью постановки
 ,
,
где m — наименьшее общее кратное чисел q,…, t.
Частные случаи:
1) если в интеграле (21) с =0, то он будет иметь вид
 , (22)
, (22)
где  ;
;
2) если b = c =0, a = d =1, то интеграл (21) примет вид
 . (23)
. (23)
Интегралы вида (22) или (23) находятся с помощью подстановки
 или
или  .
.
К интегралам от функций, рационально зависящих от тригонометрических функций, сводятся интегралы:
 (24)
(24)
подстановкой
x = a sin t; dx = a cos t dt
или
x = a cos t; dx =- a sin t dt
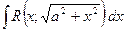 (25)
(25)
подстановкой
x = a tg t; 
или
x = a ctg t; 
 (26)
(26)
подстановкой
 ;
; 
или

Интегралы вида:
 (27)
(27)
Здесь подынтегральная функция есть рациональная функция относительно х и  . Выделив под радикалом полный квадрат и сделав подстановку
. Выделив под радикалом полный квадрат и сделав подстановку  , интегралы указанного вида приводятся к интегралам вида:
, интегралы указанного вида приводятся к интегралам вида:
 ,
,  ,
,  .
.
Интеграл от дифференциального бинома
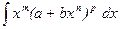 (28),
(28),
где a, b — действительные числа; m, n, p — рациональные числа, берутся, лишь в случае, когда одно из чисел р, 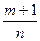 или
или 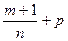 — является целым.
— является целым.
Интеграл от дифференциального бинома сводится к интегралу от рациональной функции в трёх случаях:
1) когда р — целое число,
подстановка  , где k — наименьшее общее кратное дробей m и n;
, где k — наименьшее общее кратное дробей m и n;
2) когда 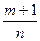 — целое число,
— целое число,
подстановкой  , где s — знаменатель дроби p;
, где s — знаменатель дроби p;
3) когда 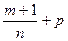 — целое число,
— целое число,
подстановкой 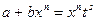 , где s — знаменатель дроби р.
, где s — знаменатель дроби р.
Во всех остальных случаях интегралы вида 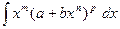 не выражаются через известные элементарные функции, т.е. «не берутся».
не выражаются через известные элементарные функции, т.е. «не берутся».
Интеграл вида:
 (29)
(29)
можно найти подстановкой  .
.
№ 7. Найти интегралы: 1)  ; 2)
; 2) 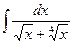 ;
;
3) 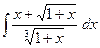 ; 4)
; 4)  ; 5)
; 5)  ;
;
6) 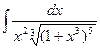 ; 7)
; 7)  ; 8)
; 8)  .
.
►1)  =
=  =
=
=  =
=  =
=  =
=
=  =
=  ;
;
2) 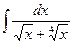 =
=  =
= 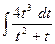 =
=  =
=
=  =
=  ;
;
3) 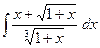 =
=  =
=  =
=
= 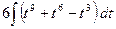 =
=  =
=
=  ;
;
4)  =
= 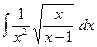 =
= 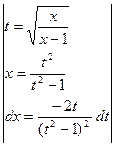 =
=
=  =
=  =
=  ;
;
5)  =
=  =
=  =
=
= 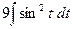 =
=  =
=  =
=
=  .
.
Замечание. Ответ можно упростить, если воспользоваться тем, что  и
и 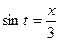 , следовательно
, следовательно
 =
=  ;
;
6) Это интеграл от дифференциального бинома.
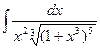 =
=  =
=
=  =
=
= 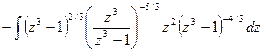 =
=
=  =
=  =
= 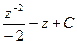 =
=  =
=
=  ;
;
7)  =
=  =
= 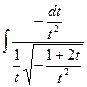 =
=
= 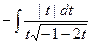 =
= 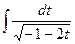 .
.
Здесь учтено, что 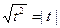 , что подынтегральная функция определена в интервале –1< x <1, вследствие чего х -1<0 и t<0 и поэтому| t |=- t.
, что подынтегральная функция определена в интервале –1< x <1, вследствие чего х -1<0 и t<0 и поэтому| t |=- t.
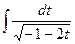 =
=  =
= 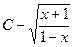 ;
;
8)  =
=  =
=  =
=
=  =
= 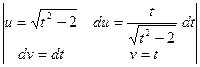 =
=
=  =
=  =
=
=  .
.
Получили возвратный интеграл. Следовательно, имеем:
 =
=  ;
;
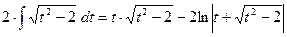 ;
;
 ;
;
Учитывая, что t = x -1, получаем
 .◄
.◄
Аудиторное занятие
№298.  . Ответ:
. Ответ:  .
.
№299.  .
.
Ответ: 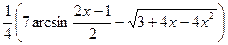 .
.
№300.  . Ответ:
. Ответ: 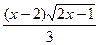 .
.
№301.  .
.
Ответ:  .
.
№302.  . Ответ:
. Ответ: 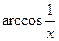 .
.
№303.  . Ответ:
. Ответ:  .
.
№304.  .
.
Ответ:  .
.
Домашнее задание
№305.  .
.
Ответ:  .
.
№306.  . Ответ:
. Ответ: 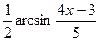 .
.
№307.  .
.
Ответ:  .
.
№308.  . Ответ:
. Ответ:  .
.
№309.  .
.
Ответ:  .
.
№310.  . Ответ:
. Ответ:  .
.
№311.  . Ответ:
. Ответ:  .
.
№312.  . Ответ:
. Ответ:  .
.
№313.  . Ответ:
. Ответ:  .
.
№314.  .
.
Ответ:  .
.
№315.  . Ответ:
. Ответ: 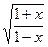 .
.
№316.  . Ответ:
. Ответ:  .
.
№317.  . Ответ:
. Ответ:  .
.
№318.  .
.
Ответ:  .
.
№319.  .
.
Ответ: 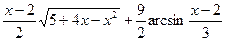 .
.
Дополнительные задания
Найти интегралы:
№320.  . Ответ:
. Ответ:  .
.
№321. 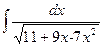 . Ответ:
. Ответ:  .
.
№322.  .
.
Ответ: 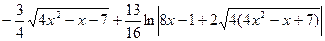 .
.
№323.  . Ответ:
. Ответ:  .
.
№324.  .
.
Ответ:  .
.
№325.  . Ответ:
. Ответ:  .
.
№326.  .
.
Ответ:  .
.
№327.  . Ответ:
. Ответ:  .
.
№328.  . Ответ:
. Ответ:  .
.
№329.  . Ответ:
. Ответ:  .
.
№330.  . Ответ:
. Ответ:  .
.
№331.  . Ответ:
. Ответ:  .
.
№332.  . Ответ:
. Ответ:  .
.
№333.  .
.
Ответ:  .
.
№334. 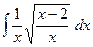 .
.
Ответ:  .
.
№335. 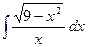 .
.
Ответ:  .
.
№336.  . Ответ:
. Ответ: 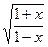 .
.
№337.  . Ответ:
. Ответ: 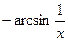 .
.
№338.  .
.
Указание. Замена  .
.
Ответ:  .
.
№339.  .
.
Указание. Избавиться от иррациональности в знаменателе подынтегральной дроби.
Ответ:  .
.
№340.  .
.
Указание. Избавиться от иррациональности в знаменателе подынтегральной дроби.
Ответ:  .
.
Примерный вариан решения
индивидуального домашнего задания
Найти интегралы:
№25. 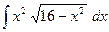 .
.
► 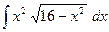 =
=  =
=
=  =
=  =
=
= 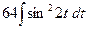 =
= 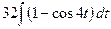 =32 t -8sin 4 t + C =
=32 t -8sin 4 t + C =
=  =
=
=  .◄
.◄
№26.  .
.
►  =
= 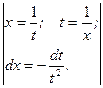 =
=
= 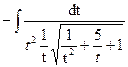 =
=  =
= 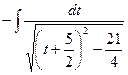 =
=
=  =
=  .◄
.◄
№36.  .
.
►  =
=  =
=
= 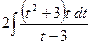 =
=  =
=
=  =
=
= 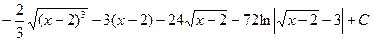 .◄
.◄
№37.  .
.
►  =
= 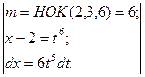 =
=
=  =
= 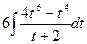 =
=
=  =
=
=  =
=
 ◄
◄
Занятие 8
Обзорное
Цели
v Знать и уметь применять основные приёмы интегрирования.
Найти интегралы:
№341.  . Ответ:
. Ответ:  .
.
№342.  . Ответ:
. Ответ:  .
.
№343. 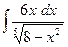 . Ответ:
. Ответ:  .
.
№344. 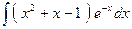 . Ответ:
. Ответ:  .
.
№345.  .
.
Ответ:  .
.
№346. 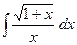 . Ответ:
. Ответ:  .
.
№347.  . Ответ:
. Ответ:  .
.
№348.  . Ответ:
. Ответ: 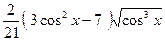 .
.
№349.  .
.
Ответ:  .
.
№350.  . Ответ:
. Ответ: 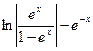 .
.
№351.  . Ответ:
. Ответ:  .
.
№352.  . Ответ:
. Ответ:  .
.
№353.  . Ответ:
. Ответ: 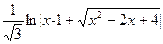 .
.
№354.  . Ответ:
. Ответ:  .
.
№355.  . Ответ:
. Ответ:  .
.
№356. 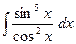 . Ответ:
. Ответ:  .
.
№357. 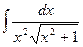 .
.
Указание. Учесть, что  .
.
Ответ: 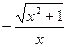 .
.
№358.  . Ответ:
. Ответ:  .
.
№359.  . Ответ:
. Ответ:  .
.
№360.  . Ответ:
. Ответ:  .
.
Примерный вариант контрольной работы
Вариант 1
Найти интегралы:
-
 .
. -
 .
. -
 .
. -
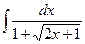 .
. -
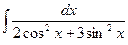 .
. -
 .
.
Вариант 2
Найти интегралы:
-
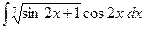 .
. -
 .
. -
 .
. -
 .
. -
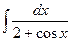 .
. -
 .
.
Контрольные вопросы
1. Первообразная и её свойства
- Может ли функция иметь единственную первообразную на некотором промежутке?
- Пусть y = F 1(x), y = F 2(x) — первообразные функции y = f (x) на некотором промежутке. Какой вид имеет график функции y = F 1 - F 2?
- Может ли функция, график которой изображён на рисунке, являться первообразной некоторой функции?

- Будет ли функция
 являться первообразной для функции
являться первообразной для функции  на про
на про



 ;
;  ;
;  , (16)
, (16) , находятся с помощью формул:
, находятся с помощью формул: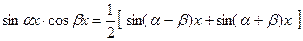 ;
; ;
; .
. , (17)
, (17)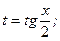



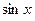 =
=  ;
;  .
. ,
, 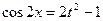 .
. .
. ;
; ,
,  .
. , (18)
, (18) ;
;  ;
;  ;
;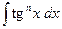 ,
,  ,
, 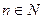 (19)
(19) ;
; ,
,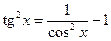 ;
;  ,
, ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5) 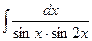 ;
; .
.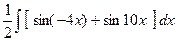 =
= =
=  ;
;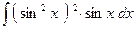 =
=  =
= =
= =
= ;
;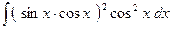 =
= =
=  =
= =
=  =
= ;
; =
=  =
=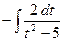 =
=  =
=  ;
; =
=  =
= =
=  =
=  =
= =
=  =
=  =
= +С;
+С; =
=  =
= 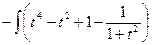 =
= =
= 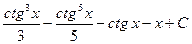 , (
, ( .◄
.◄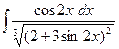 . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
.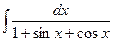 . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. .
. .
. .
. .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ: 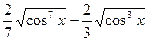 .
. . Ответ:
. Ответ:  .
.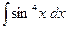 . Ответ:
. Ответ: 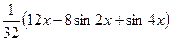 .
. . Ответ:
. Ответ:  .
. . Ответ: tg x – x.
. Ответ: tg x – x. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
.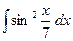 . Ответ:
. Ответ:  .
. .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
.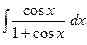 . Ответ:
. Ответ:  .
. . Ответ:
. Ответ: 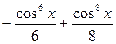 .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
.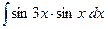 . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. .
. .
.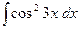 . Ответ:
. Ответ:  .
. .
. .
. .
. .
. . Ответ:
. Ответ:  .
.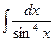 .
.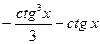 .
. . Ответ:
. Ответ: 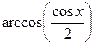 .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  , где t =tg x.
, где t =tg x. . Ответ: ln|tg x |.
. Ответ: ln|tg x |.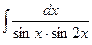 . Ответ:
. Ответ:  .
. .
. .
. . Ответ: ln|sin x |-sin x.
. Ответ: ln|sin x |-sin x. .
. .
. .
. =
= =
=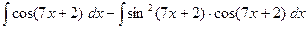 =
= .◄
.◄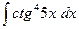 .
. =
= =
=  =
= . ◄
. ◄ .
. =
=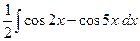 =
=  .◄
.◄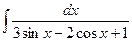 .
. =
= =
=  =
=  =
= .◄
.◄ .
. =
=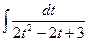 =
=  =
=  =
= .◄
.◄
 =
= =
=  =
= 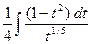 =
= =
=  =
=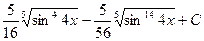 .◄
.◄ (20)
(20) , что приводит исходный интеграл к виду
, что приводит исходный интеграл к виду  .
. [11]
[11] [12].
[12]. , то под знаком радикала выделив полный квадрат, сделать подстановку
, то под знаком радикала выделив полный квадрат, сделать подстановку  , при этом исходный интеграл разбивается на сумму двух интегралов.
, при этом исходный интеграл разбивается на сумму двух интегралов. , (21)
, (21) ,
, , (22)
, (22) ;
; . (23)
. (23) или
или  .
. (24)
(24)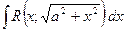 (25)
(25)

 (26)
(26) ;
; 

 (27)
(27) . Выделив под радикалом полный квадрат и сделав подстановку
. Выделив под радикалом полный квадрат и сделав подстановку  ,
,  ,
,  .
.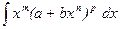 (28),
(28),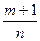 или
или 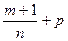 — является целым.
— является целым. , где k — наименьшее общее кратное дробей m и n;
, где k — наименьшее общее кратное дробей m и n; , где s — знаменатель дроби p;
, где s — знаменатель дроби p;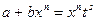 , где s — знаменатель дроби р.
, где s — знаменатель дроби р.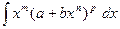 не выражаются через известные элементарные функции, т.е. «не берутся».
не выражаются через известные элементарные функции, т.е. «не берутся». (29)
(29) .
. ; 2)
; 2) 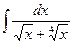 ;
;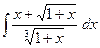 ; 4)
; 4)  ; 5)
; 5)  ;
;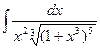 ; 7)
; 7)  ; 8)
; 8)  .
. =
= =
=  =
=  =
= =
=  ;
; =
= 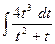 =
=  =
= =
=  ;
; =
=  =
=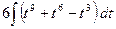 =
=  =
= ;
;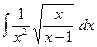 =
= 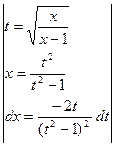 =
= =
=  =
=  ;
; =
=  =
=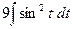 =
=  =
=  =
= .
. и
и 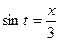 , следовательно
, следовательно ;
; =
= =
=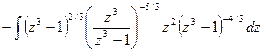 =
= =
=  =
= 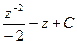 =
=  =
= ;
; =
= 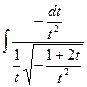 =
=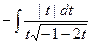 =
= 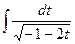 .
.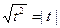 , что подынтегральная функция определена в интервале –1< x <1, вследствие чего х -1<0 и t<0 и поэтому| t |=- t.
, что подынтегральная функция определена в интервале –1< x <1, вследствие чего х -1<0 и t<0 и поэтому| t |=- t. =
= 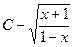 ;
; =
=  =
= =
= 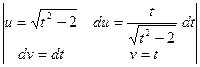 =
= =
=  =
= .
. =
= 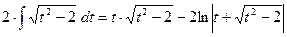 ;
; ;
; .◄
.◄ . Ответ:
. Ответ:  .
. .
.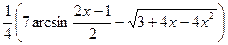 .
. . Ответ:
. Ответ: 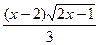 .
. .
. .
. . Ответ:
. Ответ: 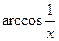 .
. . Ответ:
. Ответ:  .
. .
. .
. .
. .
. . Ответ:
. Ответ: 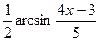 .
. .
. .
. . Ответ:
. Ответ:  .
. .
. .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. .
. .
. . Ответ:
. Ответ: 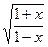 .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. .
. .
. .
.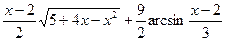 .
. . Ответ:
. Ответ:  .
.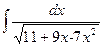 . Ответ:
. Ответ:  .
. .
.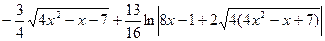 .
. . Ответ:
. Ответ:  .
. .
. .
. . Ответ:
. Ответ:  .
. .
. .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. .
. .
.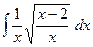 .
. .
.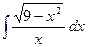 .
. .
. . Ответ:
. Ответ:  . Ответ:
. Ответ: 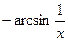 .
. .
. .
. .
. .
. .
. .
. .
.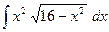 .
. =
= =
=  =
=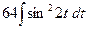 =
= 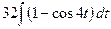 =32 t -8sin 4 t + C =
=32 t -8sin 4 t + C = =
= .◄
.◄ .
.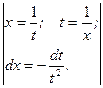 =
=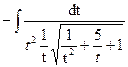 =
=  =
= 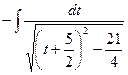 =
= =
=  .◄
.◄ .
. =
=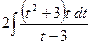 =
=  =
= =
=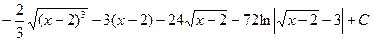 .◄
.◄ .
.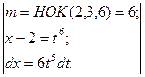 =
= =
= 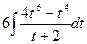 =
= =
= =
= ◄
◄ . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
.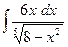 . Ответ:
. Ответ:  .
.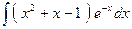 . Ответ:
. Ответ:  .
. .
. .
.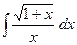 . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ: 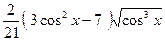 .
. .
. .
. . Ответ:
. Ответ: 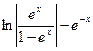 .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ: 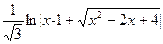 .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
.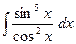 . Ответ:
. Ответ:  .
.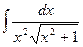 .
. .
.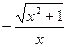 .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. . Ответ:
. Ответ:  .
. .
. .
. .
.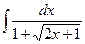 .
.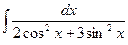 .
. .
.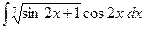 .
. .
. .
. .
. .
. .
.
 являться первообразной для функции
являться первообразной для функции  на про
на про


