Основные положения начертательной геометрии

Основные положения начертательной геометрии

Аппарат проецирования. Метод Г. Монжа.

Рис.3

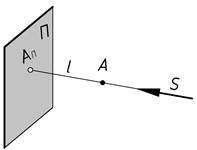
В основу построения плоских изображений положена операция проецирования, которая заключается в том, что предмет с помощью лучей проецируют на некоторую плоскость. В начертательной геометрии и в черчении для построения изображений в основном используется один из методов проецирования – параллельное ортогональное проецирование. Направление взгляда наблюдателя S перпендикулярно к плоскости проекций, относительно которой наблюдатель находится на бесконечно удаленном расстоянии (рис.3).

Проецирующий луч l от глаза наблюдателя проходит через точку A какой-либо фигуры в пространстве и пересекает плоскость проекций П, образуя ортогональную (прямоугольную) проекцию А_П. Совокупность плоскости проекций и центра проецирования называется аппаратом проецирования.

Проекцией точки на плоскость называется точка пересечения проецирующего луча с плоскостью проекций.

Чертеж должен читаться однозначно, то есть должен быть обратимым. В данном случае проекции А_П может соответствовать не только точка А, но и любая точка, принадлежащая проецирующему лучу l. Следовательно, по одной проекции, невозможно однозначно определить положение точки в пространстве.

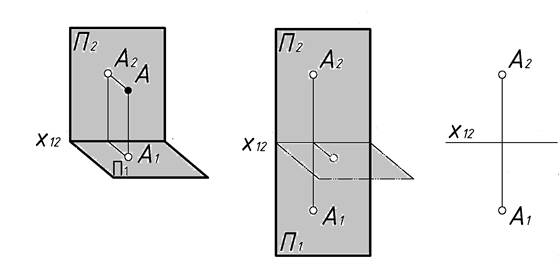
Для получения обратимых изображений точку А проецируют одновременно на две взаимно перпендикулярные плоскости: П₁ – горизонтальную и П₂ – фронтальную плоскости проекций (рис. 4а). Получим две ее проекции: горизонтальную проекцию А₁ на плоскости П₁ и фронтальную проекцию А₂ на плоскости П₂. Проецирующие прямые АА₁ и АА₂, при помощи которых точка А проецируется на плоскости проекций, определяют проецирующую плоскость А₁АА₂, перпендикулярную к обеим плоскостям проекций и к оси проекций x₁₂. Прямая А₁А₂, соединяющая две проекции точки, называется линией проекционной связи или линией связи. Линия связи всегда перпендикулярна оси x_12.

Если заданы две проекции точки А, то восстановив из них перпендикуляры к плоскостям проекций, получим точку, в которой они пересекаются. Следовательно, две проекции точки вполне определяют ее положение в пространстве. Такой метод называется методом Монжа, по имени его автора -французского ученого Гаспара Монжа (1746÷1818).

а) б) в)

Рис. 4

Для получения 2-х картинного комплексного чертежа необходимо плоскость П₁ повернуть вокруг оси x₁₂. до совмещения с плоскостью П₂ (рис. 4б). Удалить условные очертания плоскостей проекций, так как плоскости проекций безграничны. Полученное изображение называется эпюром (рис.4в).

Проекции прямой.

Из геометрии известна аксиома: через две точки можно провести одну и только одну прямую. Следовательно, прямая на эпюре определяется проекциями двух точек.

Прямые линии могут занимать по отношению к плоскостям проекций различные положения (рис.8).

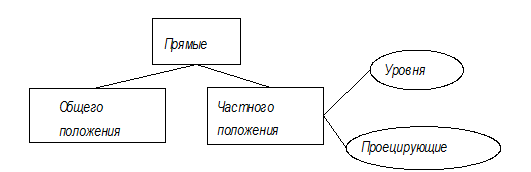
Рис.8

 

Прямые общего положения

Прямая (отрезок), не параллельная и не перпендикулярная ни к одной из плоскостей проекций, называется прямой общего положения (рис. 9).

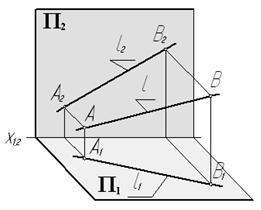
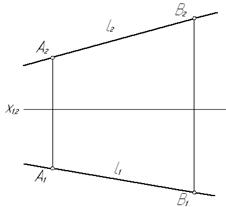
Рис. 9

Прямые уровня

Прямые, параллельные какой-либо плоскости проекций, называются прямыми уровня (таблица 2)

Таблица2

Наименование прямой	Положение прямой	Наглядное изображение	Эпюр
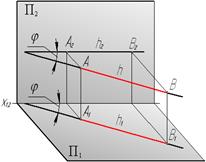
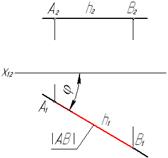
Горизонтальная (горизонталь)	АВ║П1
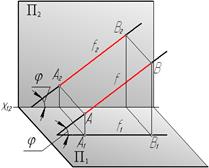
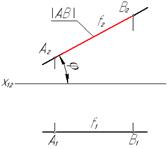
Фронтальная (фронталь)	АВ║П2
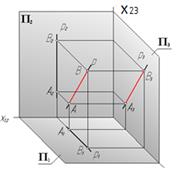
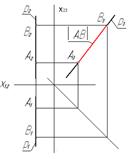
Профильная прямая	АВ║П3

 

где│АВ│ - натуральная или истинная величина отрезка.

Проецирующие прямые.

Прямые, перпендикулярные плоскостям проекций, называются проецирующими (таблица 3).

 

Таблица 3

Наименование прямой	Положение прямой	Наглядное изображение	Эпюр
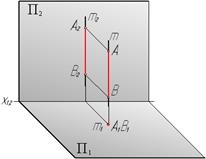
Горизонтально-проецирующая	АВ┴П1
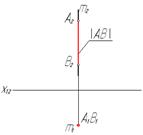
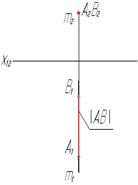
Фронтально-проецирующая	АВ┴П2
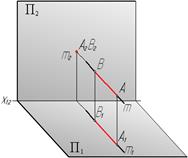
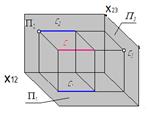
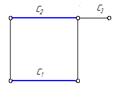
Профильно-проецирующая	с┴П3

 

Взаимное положение прямых

Пересекающиеся прямые

Пересекающиеся прямые имеют общую точку. Проекции этой точки должны принадлежать одноименным проекциям обеих прямых. Из этого следует, что точки пересечения одноименных проекций пересекающихся прямых лежат на одной линии связи. На рис. 11 изображены пересекающиеся в точке D прямые m и n.

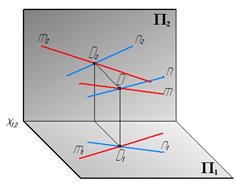
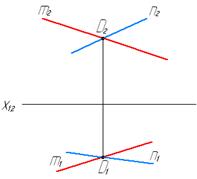
Рис. 11

Параллельные прямые

У параллельных прямых параллельны одноименные проекции. На рис. 12 изображены параллельные прямые m и n.

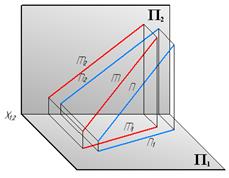
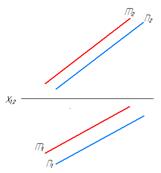
Рис. 12

Скрещивающиеся прямые.

Скрещивающиеся прямые не имеют общей точки. Следовательно, точка пересечения одноименных проекций таких прямых (например, m и n, рис. 13) не лежит на одной линии связи, так как каждая из них является изображением двух разных точек (точки 1, 2 и 3, 4).

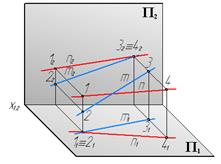
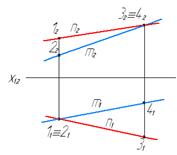
Рис.13

1.6. Способы задания плоскости. Плоскость общего положения.

Способы задания плоскости представлены в таблице 4.

Таблица 4

Способ задания	Наглядное изображение	Эпюр
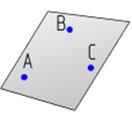
Три точки, не лежащие на одной прямой
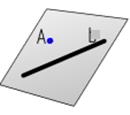
Прямой и точкой, не лежащей на этой прямой
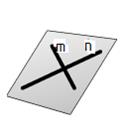
Двумя пересекающимися прямыми
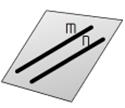
Двумя параллельными прямыми
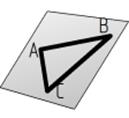
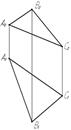
Любой плоской фигурой

Плоскости бывают общего и частного положения (рис.14)

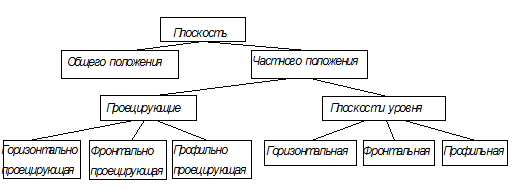
Рис.14

 

Если плоскость не перпендикулярна ни одной из плоскостей проекций, то она называется плоскостью общего положения. Примеры чертежа плоскости общего положения показаны в таблице 4.

 

Проецирующие плоскости

Если плоскость перпендикулярна только одной плоскости проекций, то она называется проецирующей (табл. 5).

 

Таблица 5

Наименование плоскости	Положение плоскости	Наглядное изображение	Эпюр
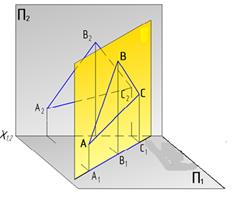
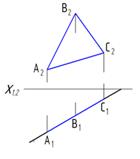
Горизонтально проецирующая	ΔАВС┴П1
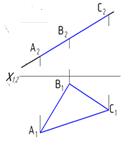
Фронтально-проецирующая	ΔАВС┴П2
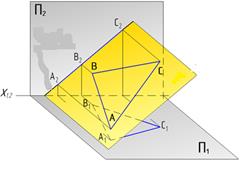
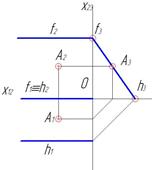
Профильно-проецирующая	α┴П3

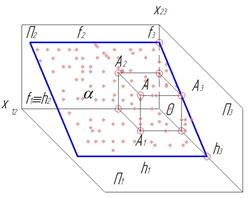
Плоскости уровня

Если плоскость перпендикулярна одновременно двум плоскостям проекций, а, следовательно, параллельна третьей, то она называется плоскостью уровня (таблица 6).

 

Таблица 6

Наименование плоскости	Положение плоскости	Наглядное изображение	Эпюр
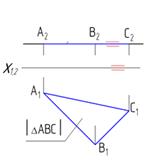
Горизонтальная	ΔАВС║П1
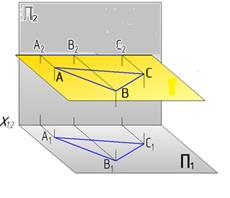
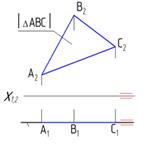
Фронтальная	ΔАВС║П2
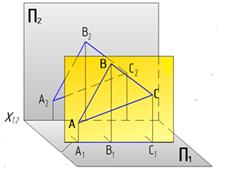
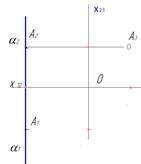
Профильная	α║П3

 

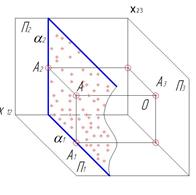
│АВС│- натуральная (истинная) величина ΔАВС.

Прямая и точка в плоскости

Прямая принадлежит плоскости, если она имеет с ней две общие точки.Точка принадлежит плоскости, если она принадлежит какой-нибудь прямой, лежащей в этой плоскости (рис. 15).Точка М принадлежит плоскости α(a∩b),так как находится на прямой k, принадлежащей этой плоскости.

 

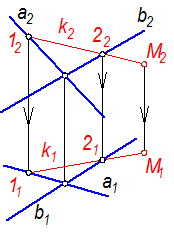
Рис. 15

Прямая принадлежит плоскости, если проходит через одну точку плоскости и параллельна какой-нибудь прямой, лежащей в этой плоскости (рис. 16). Прямая k параллельна прямой АВ.

Точка М принадлежит плоскости ΔАВС, так как находится на прямой k, принадлежащей заданной плоскости.

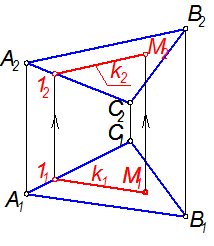
Рис.16

Фронталь плоскости.

Это прямая, принадлежащая плоскости, и параллельная фронтальной плоскости проекций (рис. 18а, б). Построение фронтали всегда начинают с горизонтальной проекции, так как она всегда параллельна оси х₁₂. Все фронтали плоскости параллельны между собой.

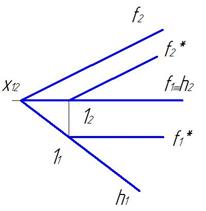
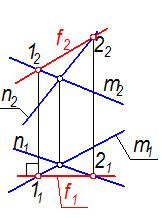
а) б)

Рис. 18

Для решения задач

Пример. Найти длину отрезка АВ.

Чтобы найти длину отрезка занимающего в пространстве общее положение относительно плоскостей П₁ и П_2, надо построить дополнительную ортогональную проекцию отрезка АВ на плоскость П₄ ему параллельную (П₄║АВ) и П₄^П₁ (рис. 24).

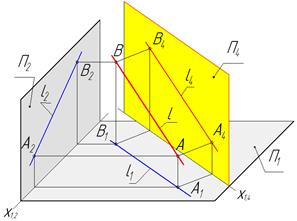
Рис.24

Поэтапное решение задачи на эпюре показано на рис. 25

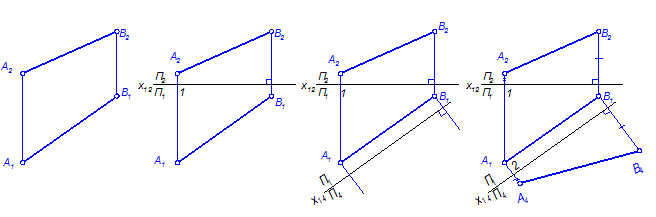
Рис. 25

Пример 2. Построить дополнительную ортогональную проекцию плоскости общего положения α(ΔАВС) на плоскости П_4,перпендикулярной к плоскости α и к плоскости П_1.

Из геометрии известно, что две плоскости взаимноперпендикулярны, если одна из них содержит прямую, перпендикулярную другой плоскости. В данном примере перпендикуляром к плоскости П₄ является горизонталь h (рис. 26).

 

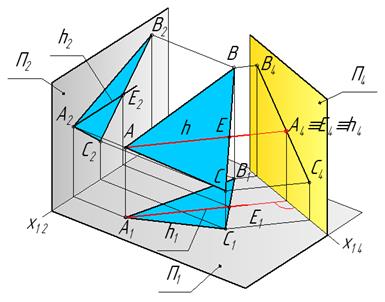
Рис. 26

Исходя из этого, ось х₁₄ проведена перпендикулярно горизонтальной проекции h₁ горизонтали h плоскости ΔАВС (рис. 27).По отношению к плоскости П₄ плоскость ΔАВС является проецирующей и изображается на ней в виде прямой А₄ В₄ С_4.

 

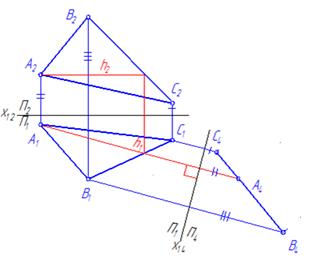
Рис. 27

Пример3. Построить дополнительную ортогональную проекцию прямой общего на плоскость ей перпендикулярную.

Для этого надо сначала построить дополнительную ортогональную проекцию прямой АВ на плоскость ей параллельную (П₄║АВ) и П₄┴П₁.Ось х₁₄ построена параллельно А₁ В₁. Затем построить дополнительную ортогональную проекцию прямой АВ на плоскость П₅ ей перпендикулярную(П₅┴ АВ) и П₅┴ П₄ (рис. 28).Ось х₄₅ построена перпендикулярно А₄ В₄._.На плоскости П₅ прямая будет точкой.

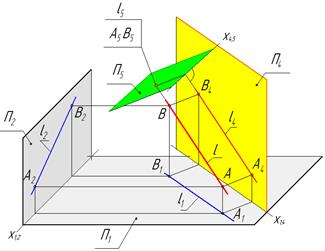
Рис. 28

Рещение задачи на эпюре показано на рис. 29

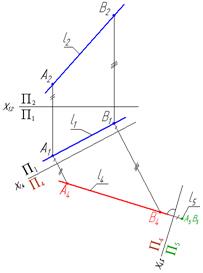
Рис. 29

Пример 4.Определить размеры треугольника АВС.

Чтобы найти величину ΔАВС,являющегося плоскостью общего положения,надо построить его дополнительную ортогональную проекцию на плоскость ему параллельную. Для этого надо сначала построить дополнительную ортогональную проекцию плоскости общего положения α(ΔАВС) на плоскости П_4,перпендикулярной к плоскости α(ΔАВС) и к плоскости П₁ (см.пример2).А затем построить его дополнительную ортогональную проекцию на плоскость П₅ ему параллельную(П_5║ ΔАВС) и П₅┴ П₄ (рис.30а).Решение задачи на эпюре показано на рис.30б.

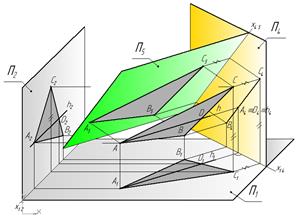
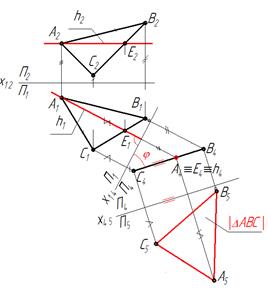
Рис. 30а Рис.30б

 

Основные положения начертательной геометрии