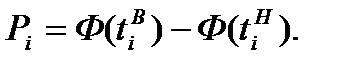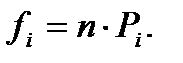Доверительным интервалом для параметра θ называется интервал]Θ—ε;Θ+ε[, который с заданной доверительной вероятностью p=1-α накрывает этот параметр. Построим доверительные интервалы для параметров нормального распределения. Это распределение имеет два параметра: m - математическое ожидание и  - среднеквадратическое отклонение. В том случае, если точечные оценки параметров m и
- среднеквадратическое отклонение. В том случае, если точечные оценки параметров m и  получены на основании выборки, доверительный интервал для математического ожидания строится с использованием квантилей распределения Стьюдента для уровня значимости α /2 и числа степеней свободы n-1 следующим образом:
получены на основании выборки, доверительный интервал для математического ожидания строится с использованием квантилей распределения Стьюдента для уровня значимости α /2 и числа степеней свободы n-1 следующим образом:

Доверительный интервал для среднеквадратического отклонения σ строится следующим образом:

где 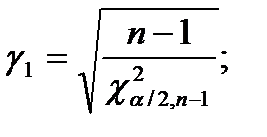

 и
и  — квантилираспределения
— квантилираспределения  ,соответствующие числу степеней свободы γ = n—1 и уровням значимости α/2 и 1-α/2. Коэффициенты
,соответствующие числу степеней свободы γ = n—1 и уровням значимости α/2 и 1-α/2. Коэффициенты  и
и  приведены в прил.
приведены в прил.
Рассмотрим пример вычисления доверительных интервалов для параметров нормального распределения по материалам вариационных рядов диаметров и высот. Используя средние арифметические двухсот измеренных диаметров и высот, вычисленные ранее и, а также среднеквадратические отклонения и исходя из предположения, что диаметры деревьев подчиняются закону нормального распределения, найдем доверительные интервалы, накрывающие параметры m и  с доверительной вероятностью 0,95. В таблице квантилей распределения Стьюдента 3 в приложении находим
с доверительной вероятностью 0,95. В таблице квантилей распределения Стьюдента 3 в приложении находим  = 1,972. Тогда доверительный интервал для среднего арифметического значения с учетом выражения будет
= 1,972. Тогда доверительный интервал для среднего арифметического значения с учетом выражения будет
диаметры
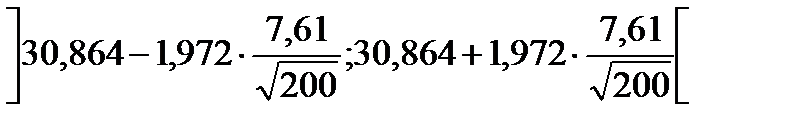 , или
, или 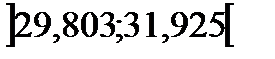 ;
;
высоты
 , или
, или  .
.
Для того чтобы вычислить границы доверительных интервалов для среднеквадратического отклонения, найдем по табл. 4 прил. коэффициенты  = 0,912 и
= 0,912 и  = 1,11 для уровня значимости α = 0,05. Используя точечные оценки среднеквадратических отклонений для данных по диаметрам и высотам и с учетом выражения, получаем доверительные интервал для среднего квадратического отклонения:
= 1,11 для уровня значимости α = 0,05. Используя точечные оценки среднеквадратических отклонений для данных по диаметрам и высотам и с учетом выражения, получаем доверительные интервал для среднего квадратического отклонения:
 , или
, или 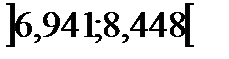 - диаметры;
- диаметры;
 , или
, или  - высоты.
- высоты.
Анализ распределения случайных величин
Любая случайная величина подчинена какому-либо, как правило, неизвестному закону распределения. Одной из задач биометрии и является определение закона распределения анализируемой случайной величины.
Нормальное распределение
Нормальное распределение имеет важное значение в биометрии. На практике очень часто исследуемые случайные величины следуют этому закону. Для того чтобы узнать, подчиняется случайная величина закону нормального распределения или нет, надо вычислить теоретические частоты вариационного ряда исходя из предположения о нормальном распределении анализируемого параметра и сравнить их с эмпирическими частотами.
Закон распределения случайной величины может быть описан с помощью функции, определяемой соотношением
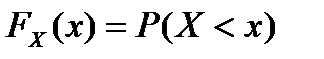
и называемой функцией распределения величины X.
Разность F(b)-F(a) представляет собой вероятность того, что случайная величина X примет значение, принадлежащее интервалу а 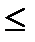 X <b, т. е. если а и b являются нижней и верхней границами интервала вариационного ряда, то вероятность попадания изучаемой случайной величины в данный интервал можно вычислить так:
X <b, т. е. если а и b являются нижней и верхней границами интервала вариационного ряда, то вероятность попадания изучаемой случайной величины в данный интервал можно вычислить так:
Pa,b=P(a 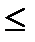 X<b)=F(b)-F(a) (1)
X<b)=F(b)-F(a) (1)
Зная эту величину, нетрудно вычислить теоретическое число наблюдений для данного интервала fa,b=n-Pa,b.
Функция нормального распределения F(x) имеет вид
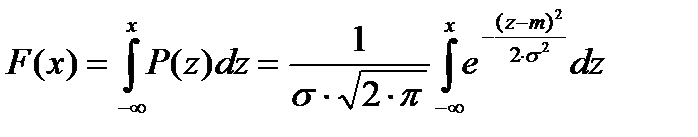 (2)
(2)
С учетом функции нормального распределения (2) выражение (1) можно переписать следующим образом:
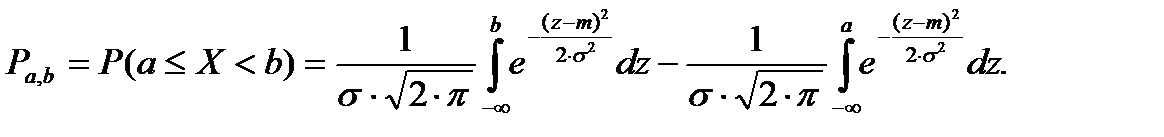 (3)
(3)
Интегралы, входящие в это выражение, нельзя выразить через элементарные функции, но их можно вычислить через специальную функцию:
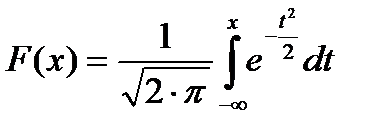 ,
,
которая является интегральной функцией нормального распределения с параметрами т = 0 и σ = 1. Для этого следует перейти к нормированной случайной величине:
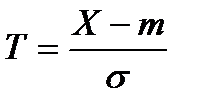 .
.
Преобразовав неравенство а 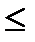 Х<b соответствующим образом, получим
Х<b соответствующим образом, получим
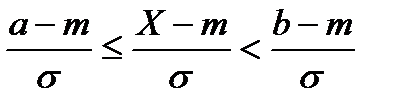 .
.
Эти два неравенства равносильны, следовательно, их вероятности равны между собой:
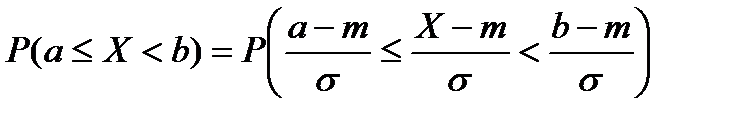 . (4)
. (4)
Используя (3) и (4), получим
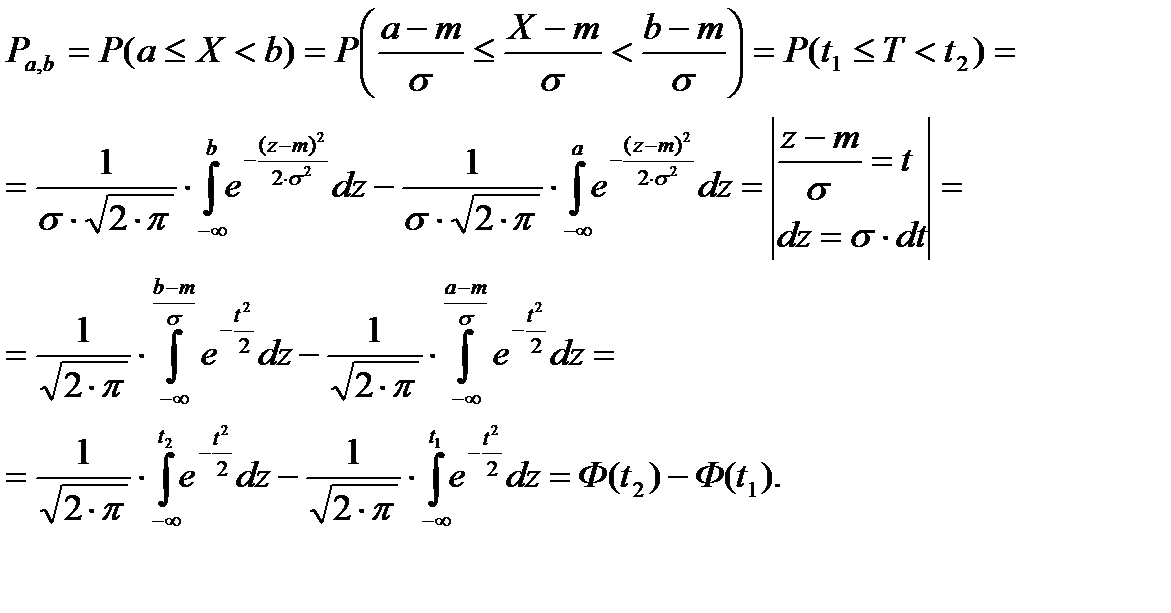 (5)
(5)
С помощью (5) и данных табл. 2 прил. мы можем вычислить теоретические частоты вариационного ряда, предполагая, что исследуемая случайная величина распределена по нормальному закону.
Выполним эту работу для вариационных рядов по диаметру и высоте. С учетом того, что оценкой параметров нормального распределения методом моментов являются среднеквадратическое отклонение и среднее арифметическое, вычислим нормированные нижнюю и верхнюю границы интервалов следующим образом:

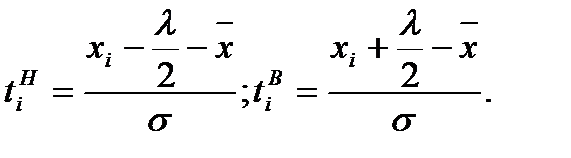
Таблица 10 ─ Вычисление теоретических частот для функции нормального распределения (диаметры).
| xi
| 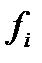
| tiн
| tiв
| Ф(tiн)
| Ф(tiв)
| Рi
| 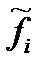
| ∆ 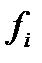 - - 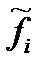
|
| 12,7
|
| -∞
| -2,17
|
| 0,015
| 0,015
| 3,
| -3,0
|
| 15,6
|
| -2,17
| -1,79
| 0,015
| 0,037
| 0,022
| 4,4
| -1,4
|
| 18,5
|
| -1,79
| -1,42
| 0,037
| 0,078
| 0,041
| 8,2
| -1,2
|
| 21,4
|
| -1,42
| -1,04
| 0,078
| 0,149
| 0,071
| 14,2
| 3,8
|
| 24,3
|
| -1,04
| -0,66
| 0,149
| 0,255
| 0,106
| 21,2
| 5,8
|
| 27,2
|
| -0,66
| -0,29
| 0,255
| 0,386
| 0,131
| 26,2
| 5,8
|
| 30,1
|
| -0,29
| 0,09
| 0,386
| 0,536
| 0,15
| 30,0
| 1,0
|
| 33,0
|
| 0,09
| 0,47
| 0,536
| 0,681
| 0,145
| 29,0
| -10,0
|
| 35,9
|
| 0,47
| 0,84
| 0,681
| 0,8
| 0,119
| 23,8
| 0,2
|
| 38,8
|
| 0,84
| 1,22
| 0,8
| 0,889
| 0,089
| 17,8
| 0,2
|
| 41,7
|
| 1,22
| 1,6
| 0,889
| 0,945
| 0,056
| 11,2
| -5,2
|
| 44,6
|
| 1,6
| 1,98
| 0,945
| 0,976
| 0,031
| 6,2
| -2,2
|
| 47,5
|
| 1,98
| 2,35
| 0,976
| 0,991
| 0,015
| 3,0
| 4,0
|
| 50,4
|
| 2,35
| 2,73
| 0,991
| 0,997
| 0,006
| 1,2
| 2,8
|
| 53,3
|
| 2,73
| +∞
| 0,997
| 1,000
| 0,003
| 0,6
| -0,6
|
| Сумма
|
| | | | | |
|
|
| | | | | | | | | | |
В отличие от анализируемого вариационного ряда, нормальное распределение определено на интервале от -∞ до +∞. Для того чтобы области определения эмпирического и нормального распределения сделать одинаковыми, добавим дополнительные интервалы перед первым интервалом с границами от -∞ до нижней границы первого интервала и после последнего интервала с границами от верхней границы последнего интервала до + ∞. Эмпирические частоты этих дополнительных интервалов будут равны нулю, так как в исходных данных нет ни одного наблюдения, которое было бы меньше нижней границы первого интервала или больше верхней границы последнего интервала. Значения функции нормированного нормального распределения для нижней 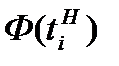 и верхней
и верхней 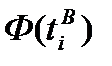 границ интервалов можно найти с помощью табл. 2, используя в качестве аргументов значения
границ интервалов можно найти с помощью табл. 2, используя в качестве аргументов значения 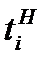 и
и 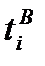 соответственно. В этой таблице значения функции распределения даны только для положительных аргументов. Если надо найти функцию распределения для отрицательного аргумента, следует воспользоваться соотношением Ф(-х)=1-Ф(х), которое справедливо, так как нормальное распределение является симметричным.
соответственно. В этой таблице значения функции распределения даны только для положительных аргументов. Если надо найти функцию распределения для отрицательного аргумента, следует воспользоваться соотношением Ф(-х)=1-Ф(х), которое справедливо, так как нормальное распределение является симметричным.
Вероятности для интервалов вариационного ряда легко вычислить как разность значений функции распределения для верхней и нижней границ:
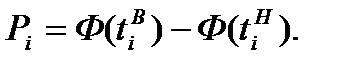
Теперь можно найти теоретические частоты ряда:
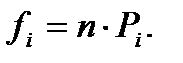
Аналогичным образом можно вычислить теоретические частоты для вариационного ряда высот (табл. 13.).
Последние колонки табл. 12 и 13, представляющие собой разность между эмпирическими и теоретическими частотами, дают нам информацию о близости теоретического (в данном случае нормального) и эмпирического распределений. Однако по данным отклонениям достаточно трудно принять решение о согласованности эмпирического и теоретического распределений. Более наглядную картину можно увидеть, изобразив эти распределения графически (рис. 8 и 9). Однако такие сравнения распределений будут субъективными. Для того чтобы дать объективную оценку согласованности эмпирических и теоретических распределений, необходимо воспользоваться специальными методиками проверки статистических гипотез.



 - среднеквадратическое отклонение. В том случае, если точечные оценки параметров m и
- среднеквадратическое отклонение. В том случае, если точечные оценки параметров m и  получены на основании выборки, доверительный интервал для математического ожидания строится с использованием квантилей распределения Стьюдента для уровня значимости α /2 и числа степеней свободы n-1 следующим образом:
получены на основании выборки, доверительный интервал для математического ожидания строится с использованием квантилей распределения Стьюдента для уровня значимости α /2 и числа степеней свободы n-1 следующим образом:

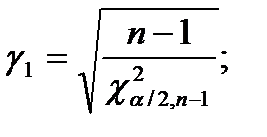

 и
и  — квантилираспределения
— квантилираспределения  ,соответствующие числу степеней свободы γ = n—1 и уровням значимости α/2 и 1-α/2. Коэффициенты
,соответствующие числу степеней свободы γ = n—1 и уровням значимости α/2 и 1-α/2. Коэффициенты  и
и  приведены в прил.
приведены в прил. = 1,972. Тогда доверительный интервал для среднего арифметического значения с учетом выражения будет
= 1,972. Тогда доверительный интервал для среднего арифметического значения с учетом выражения будет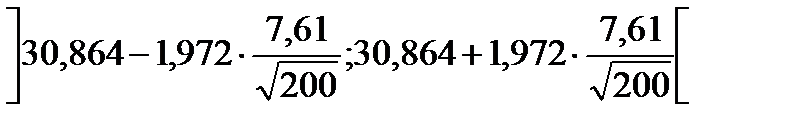 , или
, или 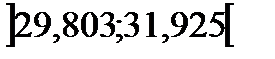 ;
; , или
, или  .
. , или
, или 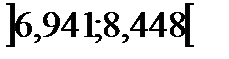 - диаметры;
- диаметры; , или
, или  - высоты.
- высоты.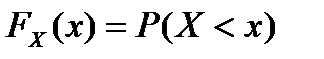
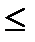 X <b, т. е. если а и b являются нижней и верхней границами интервала вариационного ряда, то вероятность попадания изучаемой случайной величины в данный интервал можно вычислить так:
X <b, т. е. если а и b являются нижней и верхней границами интервала вариационного ряда, то вероятность попадания изучаемой случайной величины в данный интервал можно вычислить так: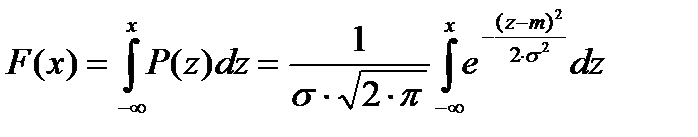 (2)
(2)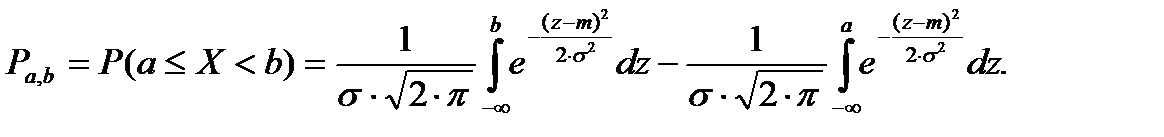 (3)
(3)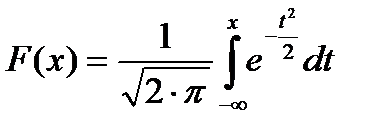 ,
,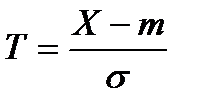 .
.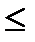 Х<b соответствующим образом, получим
Х<b соответствующим образом, получим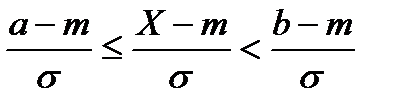 .
.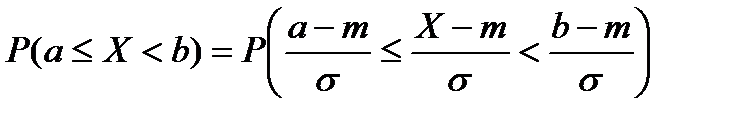 . (4)
. (4)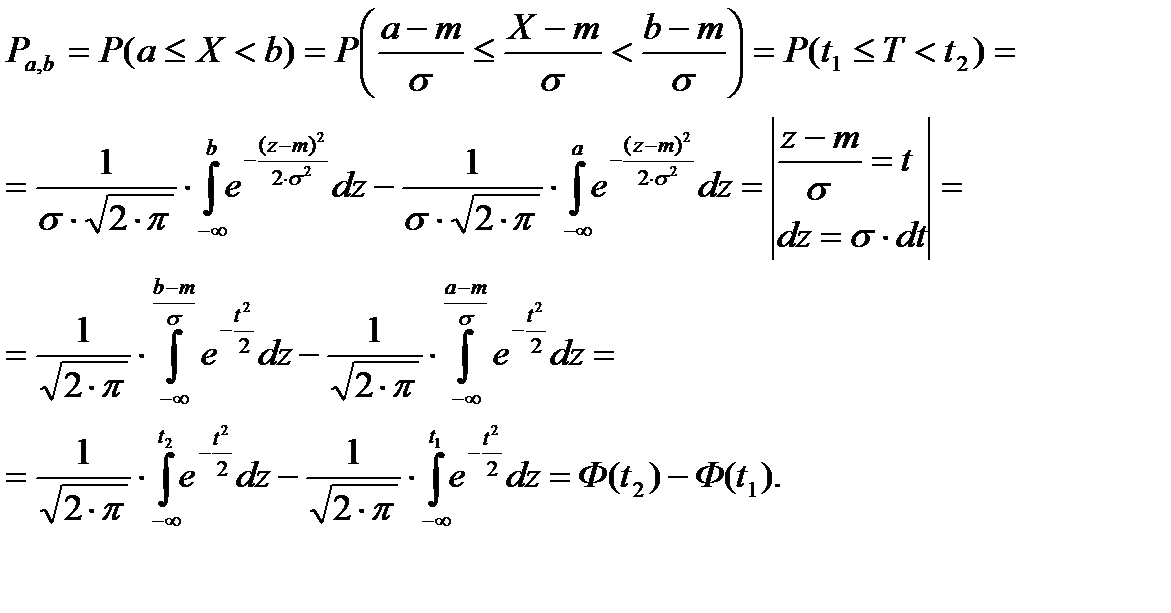 (5)
(5)
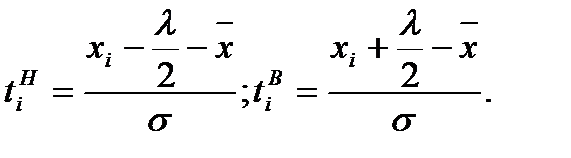
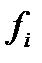
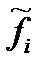
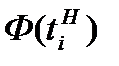 и верхней
и верхней 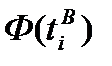 границ интервалов можно найти с помощью табл. 2, используя в качестве аргументов значения
границ интервалов можно найти с помощью табл. 2, используя в качестве аргументов значения 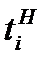 и
и 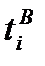 соответственно. В этой таблице значения функции распределения даны только для положительных аргументов. Если надо найти функцию распределения для отрицательного аргумента, следует воспользоваться соотношением Ф(-х)=1-Ф(х), которое справедливо, так как нормальное распределение является симметричным.
соответственно. В этой таблице значения функции распределения даны только для положительных аргументов. Если надо найти функцию распределения для отрицательного аргумента, следует воспользоваться соотношением Ф(-х)=1-Ф(х), которое справедливо, так как нормальное распределение является симметричным.