Тема: Решение систем линейных алгебраических уравнений методом Гаусса

Цель: Формирование навыков решения СЛАУ методом Гаусса.

Время выполнения: 2 часа.

Требования к выполнению практической работы:

1.Ответить на теоретические вопросы.

2.Оформить задания в тетради для практических работ.

Теоретический материал

Задачи, посвященные решению систем линейных алгебраических уравнений (СЛАУ) методом исключения неизвестных для случая, когда система линейных алгебраических уравнений имеет бесконечное множество решений (совместная неопределенная система линейных алгебраических уравнений). При решении системы предлагается использовать одну из разновидностей метода исключения неизвестных – метод Жордана – Гаусса или метода полного исключения.

В процессе решения система преобразуется в равносильные (эквивалентные) системы, то есть системы линейных алгебраических уравнений с тем же множеством решений.

К элементарным преобразованиям, сохраняющим равносильность систем линейных алгебраических уравнений, относятся следующие преобразования:

1) смена мест уравнений системы линейных алгебраических уравнений;

2) отбрасывание одного из двух одинаковых уравнений системы линейных алгебраических уравнений;

3) умножение обеих частей какого-либо уравнения на число, отличное от нуля;

4) замена одного из уравнений системы линейных алгебраических уравнений уравнением, полученным его почленным сложением с другим уравнением системы линейных алгебраических уравнений.

Сущность метода исключения состоит в том, что с помощью указанных элементарных преобразований, не нарушающих равносильности системы линейных алгебраических уравнений, выбранное неизвестное (ведущее) исключается из всех уравнений системы, кроме одного (ведущего уравнения). Метод осуществляется по шагам. На каждом шаге исключается только одно неизвестное. Шаги заканчиваются, когда ведущим побывают все уравнения системы (либо будет получено очевидное противоречие, говорящее об отсутствии решений системы линейных алгебраических уравнений).

Пример

Задание: Пользуясь методом исключения неизвестных, найти общее решение системы линейных уравнений, а также два частных ее решения, одно из которых базисное:

Решение: Система имеет размер (три уравнения, четыре неизвестных). На каждом шаге выбираем одно ведущее уравнение и в нем одно ведущее неизвестное. Ведущим каждое уравнение и каждое неизвестное могут быть только один раз. На следующем шаге их за ведущие брать нельзя.

Шаг первый. Выберем в качестве ведущего уравнения первое, а в нем ведущее неизвестное , так как коэффициент при равен единице, что упрощает вычисления.

Ведущее уравнение, то есть первое, оставляем без изменения. Исключим ведущее неизвестное из второго и третьего уравнений. Для этого нужно преобразовать эти уравнения к виду, когда коэффициенты при в них станут равными нулю.

Умножим обе части ведущего уравнения на число 7, и почленно сложим со вторым уравнением. Аналогично, умножим обе части ведущего уравнения на «-8», и почленно сложим с третьим уравнением. В итоге получим систему, равносильную исходной системе:

Теперь переменная содержится только в первом уравнении. Заметим также, что два последних уравнения станут одинаковыми, если в одном из них поменять знаки. Поэтому, отбросим одно из этих уравнений, например, третье.

Шаг второй. Выберем в качестве ведущего второе (другое) уравнение. Так как в нем нет неизвестного с коэффициентом 1, то берем любое неизвестное, с коэффициентом, отличным от нуля, и делим обе части нового ведущего уравнения на этот коэффициент. Например, выберем во втором уравнении в качестве ведущего неизвестное , с коэффициентом «-5», и поделим обе части этого уравнения на «-5»:

Чтобы исключить из первого уравнения, умножим обе части ведущего (второго) уравнения на 3 и почленно сложим с первым. Ведущее уравнение перепишем без изменения.

Ведущая переменная содержится теперь только во втором (ведущем) уравнении. Так как все уравнения уже были ведущими (каждое на своем шаге), то преобразования закончены.

Выразим из каждого уравнения то неизвестное, которое было в нем ведущим, и поэтому, не содержится в других уравнениях:

.

Получено общее решение данной системы. Переменные и , которые мы выразили, называются базисными. Остальные переменные и - называются свободными, они задаются произвольно (свободно)

Общее решение системы линейных алгебраических уравненийпредставляет собой такую запись системы линейных алгебраических уравнений, когда часть ее переменных, называемых базисными, выражены через оставшиеся переменные, называемые свободными.

Частные решения системы линейных алгебраических уравнений могут быть получены из общего решения. Для этого задаем произвольно свободные переменные и вычисляем базисные по общему решению.

Например, пусть ; . Тогда

.

Таким образом, получено частное решение системы: . Придавая свободным переменным и другие значения, найдем, аналогичным образом, любое количество частных решений СЛАУ.

Базисное решение СЛАУ, это такое частное решение, когда свободные переменные равны нулю, то есть ; 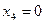, тогда . Получено базисное решение системы: .

Проверка: Проверим правильность нахождения двух частных решений, из которых базисное, подстановкой в исходную систему.

1) Проверяем решение :

таким образом, все уравнения СЛАУ выполняются.

2) Проверим решение :

.

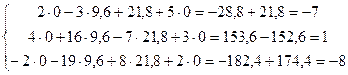Решение удовлетворяет всем уравнениям исходной СЛАУ.

Ответ: - общее решение СЛАУ,

- частное решение СЛАУ,

- базисное решение СЛАУ.

Задание для практической работы

Пользуясь методом исключения неизвестных, найдите общее решение системы линейных уравнений, а также два частных ее решения, одно из которых базисное. Для частного и базисного решений необходимо сделать проверку:

.

Контрольные вопросы:

1. Дайте определение эквивалентных (равносильных) систем линейных алгебраических уравнений.

2. Назовите элементарные преобразования, не нарушающие равносильности систем линейных алгебраических уравнений.

3. В чем состоит сущность метода Жордана – Гаусса для решения систем линейных алгебраических уравнений? Как осуществляется этот метод? Когда он применим?

4. Что называется общим решение системы линейных алгебраических уравнений?

5. Какие переменные называются базисными, а какие свободными?

6. Как найти частное решение систем линейных алгебраических уравнений? Сколько частных решений имеет система линейных алгебраических уравнений?

7. Что называется базисным решением системы линейных алгебраических уравнений? Сколько базисных решений имеет система линейных алгебраических уравнений?

Рекомендуемая литература: 1.1 [с.7-10], 1.2 [с.11-12], 2.1 [с. 91-94].

Практическая работа №5