

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...
Топ:
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре...
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Интересное:
Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Из 256 двоичных функций от трех аргументов yj=Fj(x1, x2, х3) будут рассмотрены только те, которые нашли наиболее широкое применение, их значения приведены в табл. 3.
Таблица 3
| x1 | x2 | x3 | y22 | y23 | y104 | y105 | y150 | y151 |

Рис. 6 Элементарные автоматы без памяти (двоичные функции трёх (и более) аргументов)
Функция y22 принимает единичное значение тогда и только тогда, когда ровно два входа принимают единичное значение и называется функцией исключительности. Реализуется логическим элементом "2 и только 2" (Рис. 6, а). При наличии n входов выходная переменная функции исключительности принимает единичное значение тогда и только тогда, когда заданное число аргументов k (k=n) имеют единичное значение. Данная функция реализуется логическим элементом "k и только k" (Рис. 6, б).
Функция y23 принимает единичное значение только тогда, когда не менее двух аргументов имеют единичное значение. Функция называется мажоритарной и записывается в виде:
y=x1х2Vx1x3Vx2x3.
Функция реализуется мажоритарным элементом или элементом голосования (Рис. 6, в).
При произвольном числе аргументов n и произвольном пороге r<n функция называется пороговой. Она принимает единичное значение только в том случае, когда не менее любых r аргументов имеют единичное значение и реализуется пороговым элементом (Рис. 6, г). При нечетном n и r=(n+1)/2 пороговая функция превращается в мажоритарную.
|
|
Функция y104 принимает единичное значение тогда, когда только один из ее аргументов равен 1. Данная функция называется исключающее ИЛИ и реализуется одноименным логическим элементом, УГО которого приведено на Рис. 6, д. Функция может быть от любого конечного числа аргументов (Рис. 6, е). Функция принимает единичное значение тогда и только тогда, когда любой, но только один из ее аргументов принимает единичное значение.
Функция y105 принимает единичное значение тогда и только тогда, когда нечетное число аргументов принимает единичное значение и называется функцией нечетности. Ей соответствует операция свертки по модулю два. Функция реализуется элементом свертки (Рис. 6, ж). Выходная переменная элемента свертки является суммой по модулю два значений входных переменных:
| y=x1+х2+…+xn, |
| 2 2 2 |
где + - сложение по модулю;
2 - значение модуля.
Функция нечетности от n аргументов имеет тот же физический смысл, что и функция нечетности от трех аргументов. При произвольном, но конечном числе аргументов n и произвольном модуле свертки m функция принимает вид:
| y=x1 + x2 +… + xn; |
| m m m |
где m - значение модуля.
Данная функция принимает единичное значение тогда, когда число аргументов, имеющих единичное значение, больше модуля m. Условное графическое обозначение элемента свертки по произвольному модулю m приведено на Рис. 6, з.
В дальнейшем если не указано значение модуля, то будем считать, что оно равно 2.
Функция y150 принимает единичное значение тогда и только тогда, когда четное число входов принимает единичное значение или все входы принимают нулевое значение и называется функцией четности (Рис. 6, и) и записывается в следующем виде:
y =  .
.
Функция четности по модулю два от n аргументов имеет тот же физический смысл, что и функция четности от трех аргументов. При произвольном, но конечном числе аргументов n и произвольном модуле свертки m функция четности принимает вид:
y = 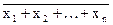 . .
|
| m m m |
Данная функция принимает единичное значение тогда, когда значения всех аргументов равны нулю либо любые m аргументов равны единице. УГО логического элемента, реализующего функцию приведено на Рис. 6, к.
|
|
Функция y151 принимает нулевое значение тогда, когда любой, но только один аргумент из трех принимает единичное значение. Функция называется исключающее ИЛИ-НЕ и реализуется одноименным логическим элементом (Рис. 6, л). При наличии любого конечного числа аргументов функция принимает нулевое значение тогда и только тогда, когда только один из аргументов принимает единичное значение. Функция реализуется логическим элементом, УГО которого приведено на Рис. 6, м. При уменьшении числа входов до двух функции исключающее ИЛИ и исключающее ИЛИ-НЕ совпадают соответственно с функциями неравнозначности и равнозначности.
Некоторые логические элементы реализуют и более сложные логические функции. Для описания функциональной зависимости таких логических элементов используются формулы или условные буквенно-цифровые обозначения (УБЦО). Условное графическое обозначение, описание функциональной зависимости между входными и выходными переменными в виде формулы и УБЦО некоторых логических элементов приведено на Рис. 7.


Рис. 7 Условное графическое и буквенно-цифровое обозначение некоторых логических элементов
|
|
|

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!