Лекция № 7
Уравнение поверхности. Общее уравнение плоскости.
Исследование общего уравнения плоскости. Угол между плоскостями. Уравнение прямой в пространстве.
Будем рассматривать поверхность, как геометрическое место точек. Уравнение  , которому удовлетворяют координаты точек поверхности, называется уравнением этой поверхности. Уравнения поверхности составляются на основании определения или свойств, присущих этой поверхности.
, которому удовлетворяют координаты точек поверхности, называется уравнением этой поверхности. Уравнения поверхности составляются на основании определения или свойств, присущих этой поверхности.
Пример: Составить уравнение поверхности, все точки которой, равноудалены от одной точки  . В декартовых координатах это уравнение имеет вид:
. В декартовых координатах это уравнение имеет вид: 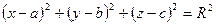 (1)
(1)
где  – расстояние от точки О до произвольной точки поверхности.
– расстояние от точки О до произвольной точки поверхности.
Уравнение (1) называется уравнением сферы.
Уравнение плоскости
 z
z
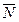 Пусть дана плоскость
Пусть дана плоскость 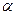 и на ней
и на ней
некоторая фиксированная точка
М  . Проведем вектор
. Проведем вектор  ,
,
перпендикулярный данной плоскости.
 Вектор
Вектор  называется нормальным
называется нормальным
вектором плоскост и или вектором нормали.
Пусть  - произвольная точка, лежащая на плоскости
- произвольная точка, лежащая на плоскости 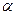 .
.
Составим вектор  , при любом расположении точки
, при любом расположении точки  он перпендикулярен вектору
он перпендикулярен вектору  . Иначе говоря, точка М, лежащая на плоскости характеризуется условием:
. Иначе говоря, точка М, лежащая на плоскости характеризуется условием: 


В этом случае  . Отсюда имеем:
. Отсюда имеем:
 (2)
(2)
Это есть искомое уравнение плоскости 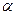 , так как ему удовлетворяют координаты точки М.
, так как ему удовлетворяют координаты точки М.
Раскрывая скобки в уравнении (2) получим:

или  (3)
(3)
Уравнение (3) называется общим уравнением плоскости.
В уравнении плоскости переменные х, у, z входят в первой степени. Следовательно, в декартовых координатах каждое уравнение первой степени определяет плоскость.
Пример: Составить уравнение плоскости, которая проходит через точку  перпендикулярно вектору
перпендикулярно вектору  .
.
Решение: Согласно уравнению (2) искомое уравнение имеет вид:

или  .
.
Уравнение плоскости «в отрезках»
Пусть дано уравнение плоскости: 
Перепишем это уравнение: 
Разделим обе части на  , получим:
, получим:
 или
или 
Обозначая: 


получим:
 (4)
(4)
Уравнение (4) называется уравнением плоскости «в отрезках». Числа  - это величины отрезков, которые отсекает данная плоскость на координатных осях.
- это величины отрезков, которые отсекает данная плоскость на координатных осях.
Пример: Составить уравнение плоскости, зная, что она отсекает на осях координат отрезки, равные 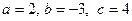 .
.
Решение: На основании (4) получим:
 или
или  .
.
Уравнение плоскости, проходящей через три данные точки
Составим уравнение плоскости, проходящей через три данные точки  и
и  .
.
Пусть точка 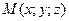 - произвольная точка искомой плоскости. Образуем векторы
- произвольная точка искомой плоскости. Образуем векторы  ,
,  и
и  . Так как эти векторы лежат в одной плоскости, значит они компланарны. Используя условие компланарности векторов, получим:
. Так как эти векторы лежат в одной плоскости, значит они компланарны. Используя условие компланарности векторов, получим:
 или
или
 (5)
(5)
Это есть уравнение плоскости, проходящей через три точки.
Пример. Составить уравнение плоскости, проходящей через точки  .
.
Решение. Используя формулу (5) уравнения плоскости, проходящей через три точки 
Получим
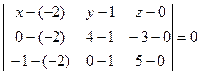 ,
, 
или  .
.
Окончательно будем иметь
 .
.
Лекция № 7
Уравнение поверхности. Общее уравнение плоскости.
Исследование общего уравнения плоскости. Угол между плоскостями. Уравнение прямой в пространстве.
Будем рассматривать поверхность, как геометрическое место точек. Уравнение  , которому удовлетворяют координаты точек поверхности, называется уравнением этой поверхности. Уравнения поверхности составляются на основании определения или свойств, присущих этой поверхности.
, которому удовлетворяют координаты точек поверхности, называется уравнением этой поверхности. Уравнения поверхности составляются на основании определения или свойств, присущих этой поверхности.
Пример: Составить уравнение поверхности, все точки которой, равноудалены от одной точки  . В декартовых координатах это уравнение имеет вид:
. В декартовых координатах это уравнение имеет вид: 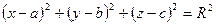 (1)
(1)
где  – расстояние от точки О до произвольной точки поверхности.
– расстояние от точки О до произвольной точки поверхности.
Уравнение (1) называется уравнением сферы.
Уравнение плоскости
 z
z
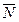 Пусть дана плоскость
Пусть дана плоскость 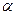 и на ней
и на ней
некоторая фиксированная точка
М  . Проведем вектор
. Проведем вектор  ,
,
перпендикулярный данной плоскости.
 Вектор
Вектор  называется нормальным
называется нормальным
вектором плоскост и или вектором нормали.
Пусть  - произвольная точка, лежащая на плоскости
- произвольная точка, лежащая на плоскости 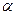 .
.
Составим вектор  , при любом расположении точки
, при любом расположении точки  он перпендикулярен вектору
он перпендикулярен вектору  . Иначе говоря, точка М, лежащая на плоскости характеризуется условием:
. Иначе говоря, точка М, лежащая на плоскости характеризуется условием: 


В этом случае  . Отсюда имеем:
. Отсюда имеем:
 (2)
(2)
Это есть искомое уравнение плоскости 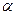 , так как ему удовлетворяют координаты точки М.
, так как ему удовлетворяют координаты точки М.
Раскрывая скобки в уравнении (2) получим:

или  (3)
(3)
Уравнение (3) называется общим уравнением плоскости.
В уравнении плоскости переменные х, у, z входят в первой степени. Следовательно, в декартовых координатах каждое уравнение первой степени определяет плоскость.
Пример: Составить уравнение плоскости, которая проходит через точку  перпендикулярно вектору
перпендикулярно вектору  .
.
Решение: Согласно уравнению (2) искомое уравнение имеет вид:

или  .
.



 , которому удовлетворяют координаты точек поверхности, называется уравнением этой поверхности. Уравнения поверхности составляются на основании определения или свойств, присущих этой поверхности.
, которому удовлетворяют координаты точек поверхности, называется уравнением этой поверхности. Уравнения поверхности составляются на основании определения или свойств, присущих этой поверхности. . В декартовых координатах это уравнение имеет вид:
. В декартовых координатах это уравнение имеет вид: 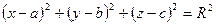 (1)
(1) – расстояние от точки О до произвольной точки поверхности.
– расстояние от точки О до произвольной точки поверхности. z
z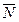 Пусть дана плоскость
Пусть дана плоскость 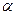 и на ней
и на ней . Проведем вектор
. Проведем вектор  ,
, Вектор
Вектор  называется нормальным
называется нормальным - произвольная точка, лежащая на плоскости
- произвольная точка, лежащая на плоскости  , при любом расположении точки
, при любом расположении точки 


 . Отсюда имеем:
. Отсюда имеем: (2)
(2)
 (3)
(3) перпендикулярно вектору
перпендикулярно вектору  .
.
 .
.
 , получим:
, получим: или
или 



 (4)
(4) - это величины отрезков, которые отсекает данная плоскость на координатных осях.
- это величины отрезков, которые отсекает данная плоскость на координатных осях.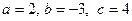 .
. или
или  .
. и
и  .
.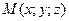 - произвольная точка искомой плоскости. Образуем векторы
- произвольная точка искомой плоскости. Образуем векторы  ,
,  и
и  . Так как эти векторы лежат в одной плоскости, значит они компланарны. Используя условие компланарности векторов, получим:
. Так как эти векторы лежат в одной плоскости, значит они компланарны. Используя условие компланарности векторов, получим: или
или (5)
(5) .
.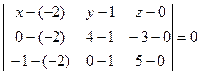 ,
, 
 .
. .
.


