1. Начинаем с последнего шага.
На последнем, n -м шаге решение принимается только из оптимальности этого шага, т. е. локально-оптимально для любого состояния системы 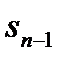 к началу этого шага. Если решается задача на максимум целевой функции, то управление
к началу этого шага. Если решается задача на максимум целевой функции, то управление  нужно выбрать так, чтобы при любых состояниях
нужно выбрать так, чтобы при любых состояниях  получить максимум целевой функции на этом шаге:
получить максимум целевой функции на этом шаге:
 (5)
(5)
Максимум показателя эффективности n -го шага, вычисленный по формуле (5), называется условным максимумом целевой функции на n-м шаге.
Максимизация проводится по всем допустимым управлениям  .
.
Соответствующее решение  , при котором достигается
, при котором достигается 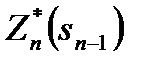 , также зависит от состояния
, также зависит от состояния  . Оно называется условным оптимальным управлением на n-м шаге и обозначается
. Оно называется условным оптимальным управлением на n-м шаге и обозначается  .
.
После решения одношаговой задачи имеем (для всех возможных состояний  ) две функции:
) две функции: 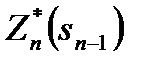 и
и  .
.
2. Рассмотрим двухшаговую задачу.
Добавим к n -му шагу (n-1)- й (рис.2).
| Рис.2. Схема двухшаговой задачи
|
Для любых состояний 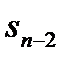 , произвольных управлений
, произвольных управлений 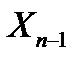 и при оптимальном управлении на последнем шаге значение целевой функции на двух последних шагах равно сумме:
и при оптимальном управлении на последнем шаге значение целевой функции на двух последних шагах равно сумме:
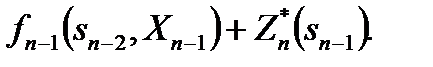 (6)
(6)
Нужно найти максимум выражения (6) по всем допустимым управлениям 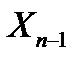 . Этот максимум зависит только от состояния к началу предпоследнего шага
. Этот максимум зависит только от состояния к началу предпоследнего шага 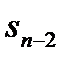 , так как значение
, так как значение 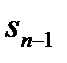 можно найти из уравнения состояния (2) при
можно найти из уравнения состояния (2) при 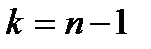 :
:
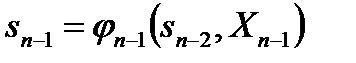 . (7)
. (7)
Максимум суммы (6) обозначается  и называется условным максимумом целевой функции при оптимальном управлении на двух последних шагах.
и называется условным максимумом целевой функции при оптимальном управлении на двух последних шагах.
 (8)
(8)
Соответствующее управление называется условным оптимальным управлением на (n–1) - м шаге и обозначается 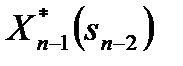 .
.
В результате максимизации получаются две функции: 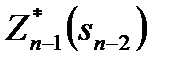 и
и  .
.
3. Общий случай. Присоединение предыдущих шагов.
| Рис.3. Схема на k -м шаге
|
Целевая функция на  последних шагах (рис.3) при произвольном управлении
последних шагах (рис.3) при произвольном управлении  на шаге k и оптимальном управлении на последующих
на шаге k и оптимальном управлении на последующих 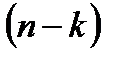 шагах равна сумме:
шагах равна сумме:
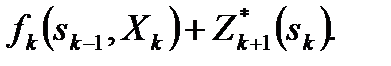 (9)
(9)
Управление  выбирается из условия максимума этой суммы. Управление, при котором достигается максимум, обозначается
выбирается из условия максимума этой суммы. Управление, при котором достигается максимум, обозначается  .
.
Максимум суммы (9) называется условным максимумом целевой функции при оптимальном управлении на k последних шагах:
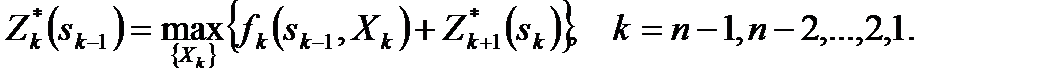 (10)
(10)
Рекуррентные уравнения (10) называются уравнениями Беллмана. Процесс нахождения оптимального решения называется условной оптимизацией.
В результате условной оптимизации получаются последовательность условных максимумов целевой функции 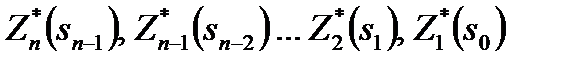 и последовательность условных оптимальных управлений
и последовательность условных оптимальных управлений 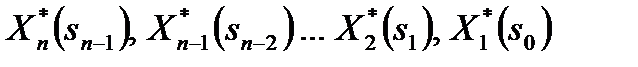 .
.
Найденное значение  является искомым максимумом целевой функции за n шагов при условии, что к началу первого шага система была в начальном состоянии
является искомым максимумом целевой функции за n шагов при условии, что к началу первого шага система была в начальном состоянии 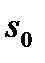 :
:
 (11)
(11)
И, наконец, записываем все решение. При фиксированном состоянии 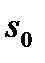 найдено оптимальное управление первого шага
найдено оптимальное управление первого шага  . Дальше следует использовать уравнения состояния (2) и последовательность условных оптимальных управлений для получения следующей цепочки результатов:
. Дальше следует использовать уравнения состояния (2) и последовательность условных оптимальных управлений для получения следующей цепочки результатов:
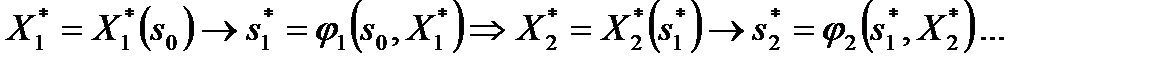
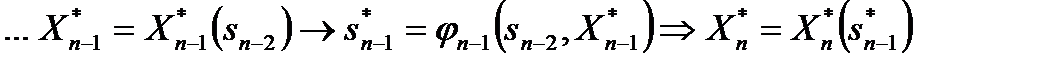 (12)
(12)
Примеры решения задач динамического программирования
Рассмотрим применение метода динамического программирования на конкретных задачах.
Выбор оптимального маршрута
Постановка задачи.
Пусть известна схема возможных маршрутов движения от пункта А до пункта Б (рис.4). Схема представляет собой ориентированный граф, вершины которого соответствуют промежуточным пунктам, ребра – возможным вариантам перемещения между соседними пунктами.
Весь маршрут от пункта А до пункта Б можно разбить на n шагов. В данной схеме n=4. Состояния системы определяются следующим образом: 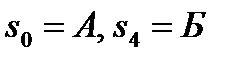 , промежуточные состояния определяются номерами промежуточных пунктов
, промежуточные состояния определяются номерами промежуточных пунктов 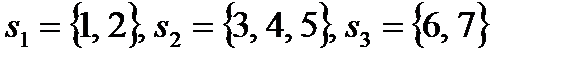 .
.
Показателем эффективности 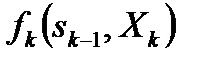 каждого шага в зависимости от целей исследования может служить расстояние между двумя смежными пунктами i и j, стоимость проезда, затраты времени, топлива или иных ресурсов. Для определенности в данном примере в качестве показателя эффективности рассмотрим стоимость проезда
каждого шага в зависимости от целей исследования может служить расстояние между двумя смежными пунктами i и j, стоимость проезда, затраты времени, топлива или иных ресурсов. Для определенности в данном примере в качестве показателя эффективности рассмотрим стоимость проезда 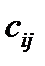 между двумя смежными пунктами i и j. Управление
между двумя смежными пунктами i и j. Управление 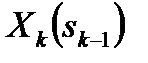 в данной задаче – это выбор возможного перемещения на шаге k из пункта i в пункт j. Целевая функция
в данной задаче – это выбор возможного перемещения на шаге k из пункта i в пункт j. Целевая функция 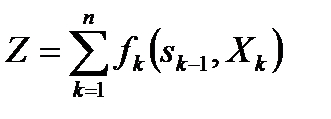 определяет суммарную стоимость проезда от пункта А до пункта Б. Необходимо из всех возможных маршрутов выбрать оптимальный, чтобы общая стоимость проезда была минимальной.
определяет суммарную стоимость проезда от пункта А до пункта Б. Необходимо из всех возможных маршрутов выбрать оптимальный, чтобы общая стоимость проезда была минимальной.
Применительно к данной задаче уравнения Беллмана (10) соответствуют вычислению минимальной стоимости последующего пути из пункта i до пункта Б, начиная с шага k:
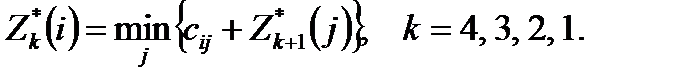 (13)
(13)
где 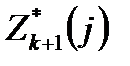 – минимальная стоимость проезда от пункта j до конечного пункта Б.
– минимальная стоимость проезда от пункта j до конечного пункта Б.
Решение задачи.
Начинаем поиск оптимального маршрута с последнего шага (рис.5), локально-оптимальные решения каждого шага выделим жирной линией:
k =4

Переходим к предыдущему шагу, определяем оптимальные решения на двух последних шагах (рис.6):
Шаг k =3.
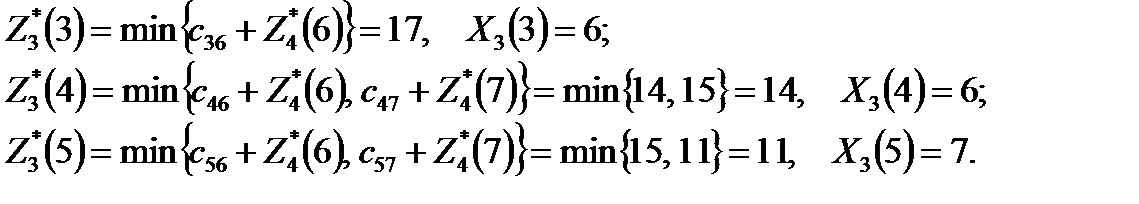
Переходим к предыдущему шагу, определяем оптимальные решения на трех последних шагах (рис.7):
Шаг k =2.

Для первого шага получаем (рис.8):
Шаг k =1.

Минимальная суммарная стоимость проездаот пункта А до пункта Б равна  . В процессе решения получены две последовательности оптимальных решений и соответствующих состояний (пунктов), так как при k =2 существует 2 оптимальных дальнейших маршрута. На рис.8 оптимальные решения выделены непрерывными ломаными линиями от пункта А до пункта Б.
. В процессе решения получены две последовательности оптимальных решений и соответствующих состояний (пунктов), так как при k =2 существует 2 оптимальных дальнейших маршрута. На рис.8 оптимальные решения выделены непрерывными ломаными линиями от пункта А до пункта Б.
Первое оптимальное решение (маршрут А – 2 – 4 – 6 – Б):
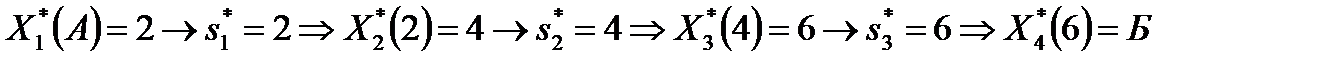 .
.
Второе оптимальное решение (маршрут А – 2 – 5 – 7 – Б):
 .
.



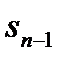 к началу этого шага. Если решается задача на максимум целевой функции, то управление
к началу этого шага. Если решается задача на максимум целевой функции, то управление  нужно выбрать так, чтобы при любых состояниях
нужно выбрать так, чтобы при любых состояниях  получить максимум целевой функции на этом шаге:
получить максимум целевой функции на этом шаге: (5)
(5)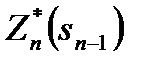 , также зависит от состояния
, также зависит от состояния  .
.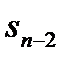 , произвольных управлений
, произвольных управлений 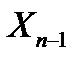 и при оптимальном управлении на последнем шаге значение целевой функции на двух последних шагах равно сумме:
и при оптимальном управлении на последнем шаге значение целевой функции на двух последних шагах равно сумме: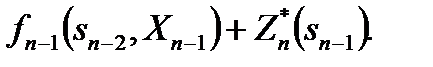 (6)
(6)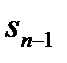 можно найти из уравнения состояния (2) при
можно найти из уравнения состояния (2) при 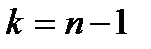 :
: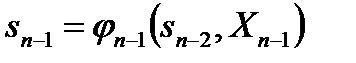 . (7)
. (7) и называется условным максимумом целевой функции при оптимальном управлении на двух последних шагах.
и называется условным максимумом целевой функции при оптимальном управлении на двух последних шагах. (8)
(8)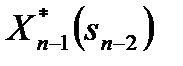 .
.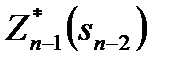 и
и  .
. последних шагах (рис.3) при произвольном управлении
последних шагах (рис.3) при произвольном управлении  на шаге k и оптимальном управлении на последующих
на шаге k и оптимальном управлении на последующих 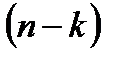 шагах равна сумме:
шагах равна сумме: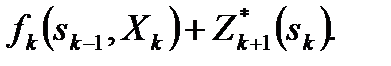 (9)
(9) .
.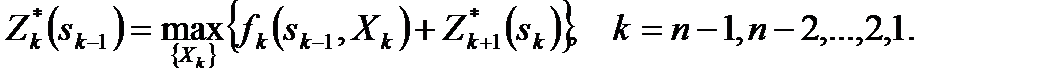 (10)
(10)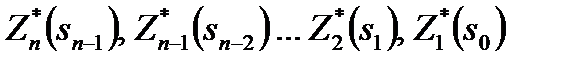 и последовательность условных оптимальных управлений
и последовательность условных оптимальных управлений 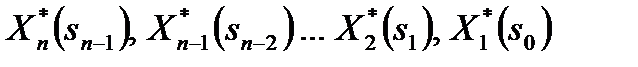 .
. является искомым максимумом целевой функции за n шагов при условии, что к началу первого шага система была в начальном состоянии
является искомым максимумом целевой функции за n шагов при условии, что к началу первого шага система была в начальном состоянии 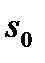 :
: (11)
(11) . Дальше следует использовать уравнения состояния (2) и последовательность условных оптимальных управлений для получения следующей цепочки результатов:
. Дальше следует использовать уравнения состояния (2) и последовательность условных оптимальных управлений для получения следующей цепочки результатов: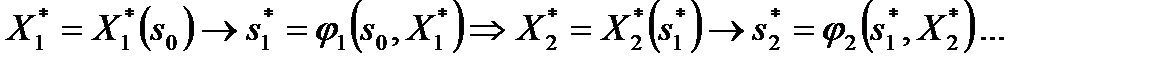
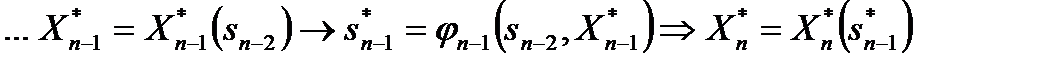 (12)
(12)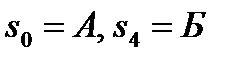 , промежуточные состояния определяются номерами промежуточных пунктов
, промежуточные состояния определяются номерами промежуточных пунктов 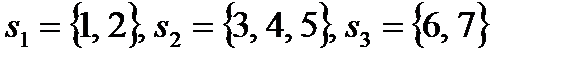 .
.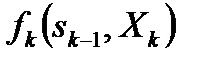 каждого шага в зависимости от целей исследования может служить расстояние между двумя смежными пунктами i и j, стоимость проезда, затраты времени, топлива или иных ресурсов. Для определенности в данном примере в качестве показателя эффективности рассмотрим стоимость проезда
каждого шага в зависимости от целей исследования может служить расстояние между двумя смежными пунктами i и j, стоимость проезда, затраты времени, топлива или иных ресурсов. Для определенности в данном примере в качестве показателя эффективности рассмотрим стоимость проезда 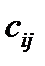 между двумя смежными пунктами i и j. Управление
между двумя смежными пунктами i и j. Управление 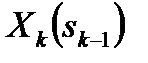 в данной задаче – это выбор возможного перемещения на шаге k из пункта i в пункт j. Целевая функция
в данной задаче – это выбор возможного перемещения на шаге k из пункта i в пункт j. Целевая функция 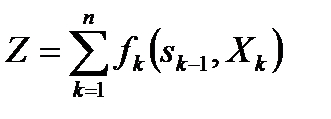 определяет суммарную стоимость проезда от пункта А до пункта Б. Необходимо из всех возможных маршрутов выбрать оптимальный, чтобы общая стоимость проезда была минимальной.
определяет суммарную стоимость проезда от пункта А до пункта Б. Необходимо из всех возможных маршрутов выбрать оптимальный, чтобы общая стоимость проезда была минимальной.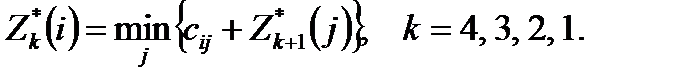 (13)
(13)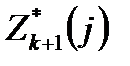 – минимальная стоимость проезда от пункта j до конечного пункта Б.
– минимальная стоимость проезда от пункта j до конечного пункта Б.
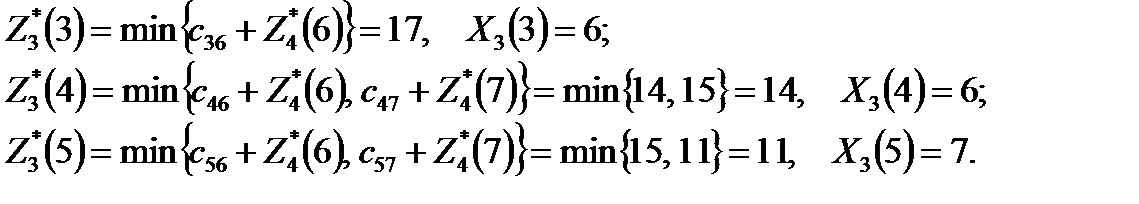


 . В процессе решения получены две последовательности оптимальных решений и соответствующих состояний (пунктов), так как при k =2 существует 2 оптимальных дальнейших маршрута. На рис.8 оптимальные решения выделены непрерывными ломаными линиями от пункта А до пункта Б.
. В процессе решения получены две последовательности оптимальных решений и соответствующих состояний (пунктов), так как при k =2 существует 2 оптимальных дальнейших маршрута. На рис.8 оптимальные решения выделены непрерывными ломаными линиями от пункта А до пункта Б.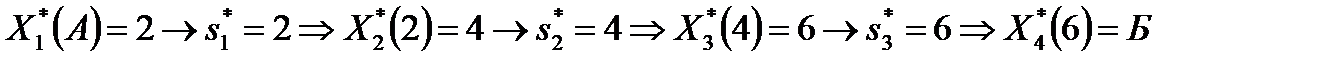 .
. .
.


