Доказательство.

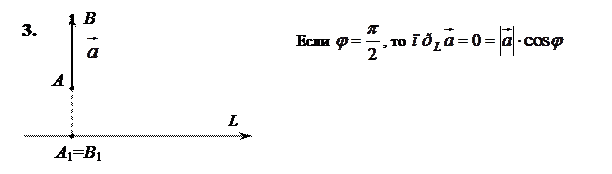
,
Следствие 1.1. Проекция вектора на ось положительная (отрицательная), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой.
Следствие 1.2. Проекции равных векторов на одну и ту же ось равны между собой.
Свойство 2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось, т.е.
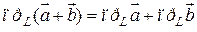 .
.
Свойство 3. При умножении вектора 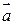 на число l его проекция на ось также умножается на это число, т.е.
на число l его проекция на ось также умножается на это число, т.е.
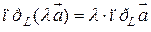 .
.
Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.
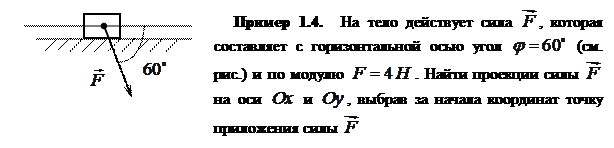
Решение.
Выбираем произвольно оси координат 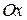 и
и 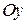 , где точка
, где точка 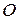 − начала системы координат.
− начала системы координат.
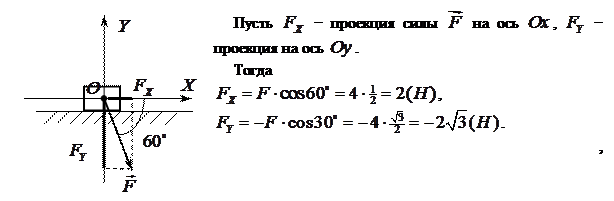
Приложения геометрического вектора
Декартовы прямоугольные координаты вектора.
Линейные операции над векторами
Линейные операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов.
1. При сложении (вычитании) векторов их одноименные координаты складываются (вычитаются), т.е.
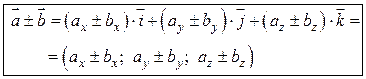 . (2.8)
. (2.8)
2. При умножении вектора на скаляр координаты вектора умножаются на этот скаляр, т.е.
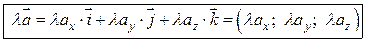 . (2.9)
. (2.9)
Равенство векторов
Из определения вектора как направленного отрезка, который можно передвигать в пространстве параллельно самому себе, следует, что два вектора 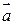 и
и 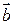 равны тогда и только тогда, когда выполняются равенства:
равны тогда и только тогда, когда выполняются равенства: 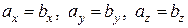 , т.е.
, т.е.
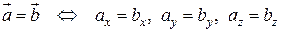 .
.
Операции сумма, разность двух векторов и умножение вектора на число, а также и равенство векторов, можно обобщить на n -мерный вектор.
Пример 2.1. Найти координаты и длину вектора 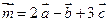 , если
, если 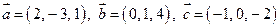 . Найти координаты орта вектора
. Найти координаты орта вектора 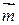 .
.
Решение. Согласно формулам (2.8) и (2.9) находим координаты вектора 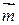 :
:
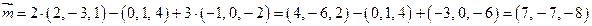 .
.
По формуле (2.3) находим длину вектора 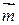 :
:
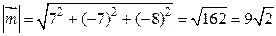 .
.
Координаты орта (единичного вектора) вектора 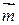 находятся по следующим формулам:
находятся по следующим формулам:
 ,
,
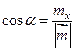 ,
, 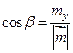 ,
, 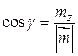 .
.
Тогда получаем
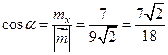 ,
, 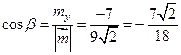 ,
, 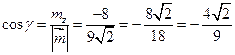 .
.
Таким образом,
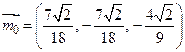
,
Коллинеарность векторов
Выясним условие коллинеарности векторов 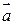 и
и 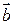 , заданных своими координатами.
, заданных своими координатами.
Так как 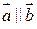 , то можно записать
, то можно записать 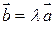 , где l - некоторое действительное число. То есть
, где l - некоторое действительное число. То есть
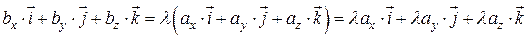 .
.
Отсюда
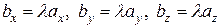 ,
,
т.е.
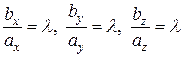 или
или 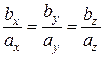 .
.
Значит, координаты коллинеарных векторов пропорциональны. Верно и обратное утверждение: векторы, имеющие пропорциональные координаты, коллинеарны.
Таким образом, два вектора 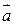 и
и 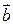 коллинеарны тогда и только тогда, когда их координаты соответственно пропорциональны, т.е.
коллинеарны тогда и только тогда, когда их координаты соответственно пропорциональны, т.е.
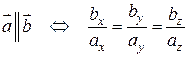 .
.
Пример 2.2. Коллинеарны ли векторы 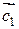 и
и 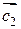 , построенные на векторах
, построенные на векторах 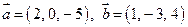 , если
, если 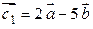 и
и 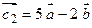 ?
?
Решение. Коллинеарность векторов 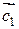 и
и 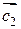 означает пропорциональность их координат. Имеем
означает пропорциональность их координат. Имеем
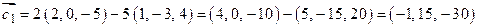 ,
, 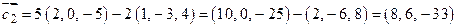 .
.
Так как 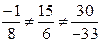 , т.е. координаты векторов
, т.е. координаты векторов 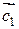 и
и 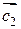 не пропорциональны, следовательно, эти векторы не коллинеарны.
не пропорциональны, следовательно, эти векторы не коллинеарны.
,
Радиус-вектор. Координаты точки.
Решение.
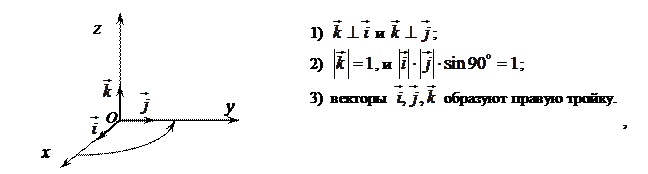
Линейно зависимые и линейно независимые
Системы векторов
Выше были введены операции над векторами, находящимися на плоскости ( ) или в 3-х-мерном пространстве (
) или в 3-х-мерном пространстве (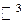 ). Так же было определено понятие «n -мерный вектор», и введены операции над ними в n -мерном пространстве.
). Так же было определено понятие «n -мерный вектор», и введены операции над ними в n -мерном пространстве.
Если мы в n -мерном пространстве рассматриваем точку 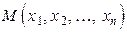 , то этой точке можно поставить в соответствие радиус-вектор
, то этой точке можно поставить в соответствие радиус-вектор 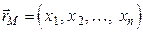 . Можно сформулировать и обратное утверждение: каждому радиус-вектору
. Можно сформулировать и обратное утверждение: каждому радиус-вектору 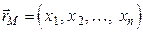 ставиться в соответствие точка
ставиться в соответствие точка 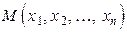 , т.е.
, т.е.
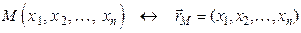 .
.
Теперь можно ввести корректное понятие «n -мерное векторное пространство».
Определение 6.1. Множество всех n -мерных векторов, в котором для любых двух векторов определена их сумма, и для любого действительного числа определено произведение вектора на это число, называется действительнымn-мерных векторным арифметическим пространством  .
.
Если в n -мерном векторном пространстве  введена операция скалярного умножения, то оно называется евклидовым пространством.
введена операция скалярного умножения, то оно называется евклидовым пространством.
Надо отметить, что любую совокупность векторов 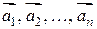 пространства
пространства 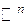 можно считать как систему векторов.
можно считать как систему векторов.
Для характеристики взаимного расположения векторов в пространстве вводится понятие линейной зависимости между векторами.
Определение 6.2. Вектор 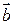 называется линейной комбинациейвекторов системы
называется линейной комбинациейвекторов системы 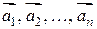 , если существуют такие числа
, если существуют такие числа 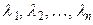 , что
, что
 . (6.1)
. (6.1)
Числа 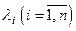 называются коэффициентами линейной комбинации. В этом случае говорят, что вектор
называются коэффициентами линейной комбинации. В этом случае говорят, что вектор 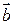 линейно выражается через систему векторов
линейно выражается через систему векторов 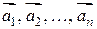 или вектор
или вектор 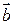 разложен по векторам системы
разложен по векторам системы 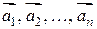 . Введением понятия линейной комбинации мы объединили понятия сложения векторов и умножения вектора на число.
. Введением понятия линейной комбинации мы объединили понятия сложения векторов и умножения вектора на число.
Определение 6.3. Система векторов 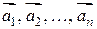 называется линейно зависимой, если существуют такие числа
называется линейно зависимой, если существуют такие числа 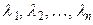 , из которых хотя бы одно отлично от нуля, что
, из которых хотя бы одно отлично от нуля, что
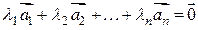 . (6.2)
. (6.2)
В противном случае векторы 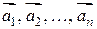 называются линейно независимыми.
называются линейно независимыми.
Приведем теоремы (без доказательства), устанавливающие условия линейной зависимости векторов на плоскости и в 3-х-мерном пространстве.
Теорема 6.1. Любые два коллинеарных вектора линейно зависимы, а два неколлинеарных вектора линейно независимы.
Теорема 6.2. Три компланарных вектора линейно зависимы, а три некомпланарных вектора линейно независимы.
Пример 6.1. Выяснить, будет ли данная система векторов линейно зависимой или независимой
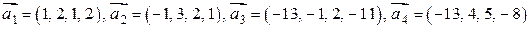 .
.
Решение. Составим их линейную комбинацию:
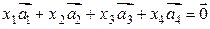
или
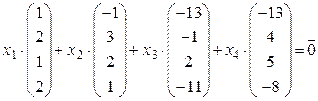 .
.
Такое векторное уравнение эквивалентно следующей системе уравнений:
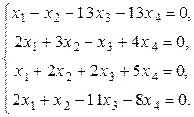 .
.
Составляем матрицу системы и приводим к ступенчатому виду:
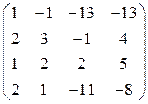 ~
~ 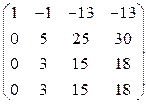 ~
~ 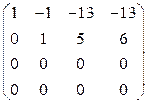 .
.
Последняя матрица равносильна следующей системе уравнений:
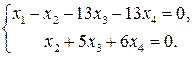
Можно не решая системы уравнений сказать, что система имеет бесчисленное множество решений, среди которых есть ненулевое. Значит, система векторов линейно зависима.
Например, частным решением является: 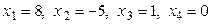 . Значит,
. Значит, 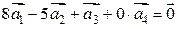 , т.е. указанная система векторов линейно зависима.
, т.е. указанная система векторов линейно зависима.
,
Базис системы векторов.
Доказательство.

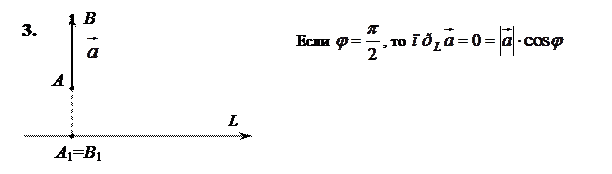
,
Следствие 1.1. Проекция вектора на ось положительная (отрицательная), если вектор образует с осью острый (тупой) угол, и равна нулю, если этот угол – прямой.
Следствие 1.2. Проекции равных векторов на одну и ту же ось равны между собой.
Свойство 2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось, т.е.
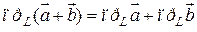 .
.
Свойство 3. При умножении вектора 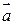 на число l его проекция на ось также умножается на это число, т.е.
на число l его проекция на ось также умножается на это число, т.е.
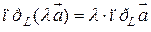 .
.
Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.
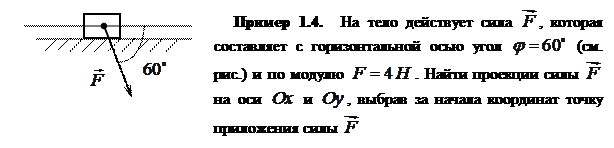
Решение.
Выбираем произвольно оси координат 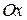 и
и 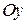 , где точка
, где точка 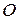 − начала системы координат.
− начала системы координат.
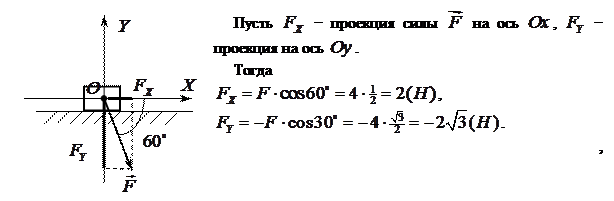
Приложения геометрического вектора




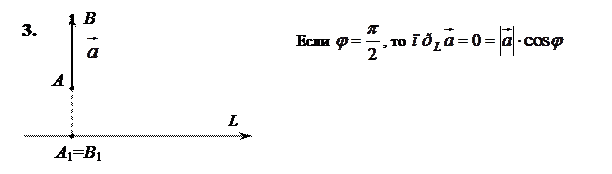
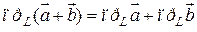 .
. на число l его проекция на ось также умножается на это число, т.е.
на число l его проекция на ось также умножается на это число, т.е.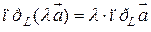 .
.
 и
и  , где точка
, где точка 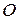 − начала системы координат.
− начала системы координат.
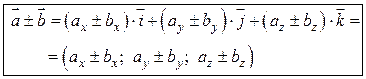 . (2.8)
. (2.8)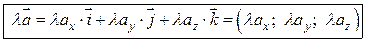 . (2.9)
. (2.9)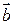 равны тогда и только тогда, когда выполняются равенства:
равны тогда и только тогда, когда выполняются равенства: 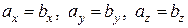 , т.е.
, т.е.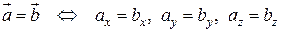 .
.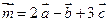 , если
, если 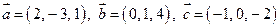 . Найти координаты орта вектора
. Найти координаты орта вектора 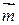 .
.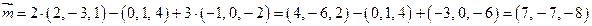 .
.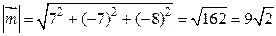 .
.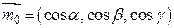 ,
,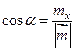 ,
, 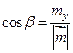 ,
, 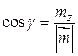 .
.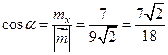 ,
, 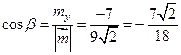 ,
, 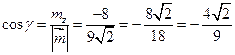 .
.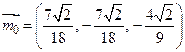
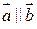 , то можно записать
, то можно записать 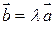 , где l - некоторое действительное число. То есть
, где l - некоторое действительное число. То есть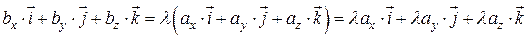 .
.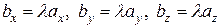 ,
,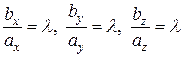 или
или 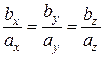 .
.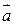 и
и 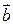 коллинеарны тогда и только тогда, когда их координаты соответственно пропорциональны, т.е.
коллинеарны тогда и только тогда, когда их координаты соответственно пропорциональны, т.е.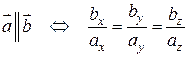 .
.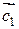 и
и 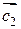 , построенные на векторах
, построенные на векторах 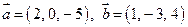 , если
, если 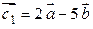 и
и 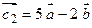 ?
?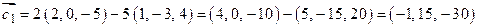 ,
, 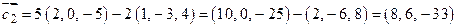 .
.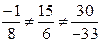 , т.е. координаты векторов
, т.е. координаты векторов 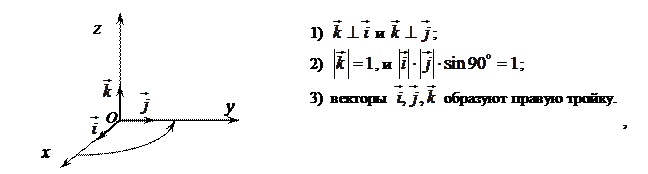
 ) или в 3-х-мерном пространстве (
) или в 3-х-мерном пространстве ( ). Так же было определено понятие «n -мерный вектор», и введены операции над ними в n -мерном пространстве.
). Так же было определено понятие «n -мерный вектор», и введены операции над ними в n -мерном пространстве.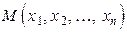 , то этой точке можно поставить в соответствие радиус-вектор
, то этой точке можно поставить в соответствие радиус-вектор  . Можно сформулировать и обратное утверждение: каждому радиус-вектору
. Можно сформулировать и обратное утверждение: каждому радиус-вектору 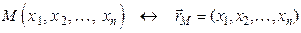 .
. .
.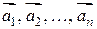 пространства
пространства 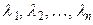 , что
, что . (6.1)
. (6.1)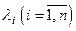 называются коэффициентами линейной комбинации. В этом случае говорят, что вектор
называются коэффициентами линейной комбинации. В этом случае говорят, что вектор 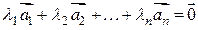 . (6.2)
. (6.2)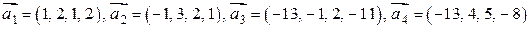 .
.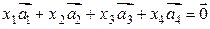
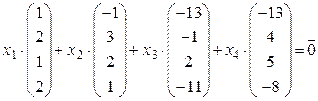 .
.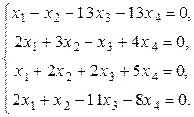 .
.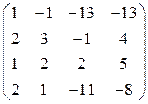 ~
~ 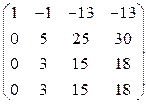 ~
~ 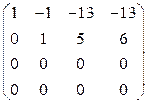 .
.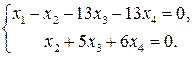
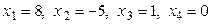 . Значит,
. Значит, 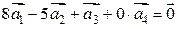 , т.е. указанная система векторов линейно зависима.
, т.е. указанная система векторов линейно зависима.


