Для спектрального представления непериодических (импульсных) сигналов s (t), заданных на конечном интервале (t 1, t 2) (рис. 3.3), непосредственно воспользоваться рядом Фурье нельзя. Для гармонического разложения сигнала мысленно дополняют его такими же импульсными сигналами до периодического с некоторым интервалом Т (рис. 3.3).

Рис. 3.3. Импульсный сигнал s (t) и его периодическое продолжение s пер(t + kT)
Для того чтобы вне искусственно введенного интервала исходный сигнал был равен нулю, необходимо увеличить период повторения импульсов.
В пределе, при увеличении периода ∞ → Т все импульсы уйдут право и влево в бесконечность и периодическая последовательность вновь станет одиночным импульсом.
Для вычисления спектра удобна симметричная комплексная форма ряда Фурье, но в нем вместо суммы будет интеграл с бесконечными пределами (преобразование Фурье):
 . (3.3)
. (3.3)
При таком предельном переходе основная частота сигнала Ω = 2 π / T стремится к нулю, бесконечно увеличивается число спектральных составляющих, частоты соседних гармоник k Ω и (k + 1)Ω становятся неразличимыми, а спектр будет сплошным.
Функция G (j Ω) называется спектральной плотностью сигнала х (t).
Функции G (j Ω) и s (t) представляют собой две математические модели одного и того же физического процесса: одна из них отражает частотный состав сигнала, а другая описывает изменение сигнала с течением времени.
Спектральная плотность сигнала определяется с использованием прямого преобразования Фурье:
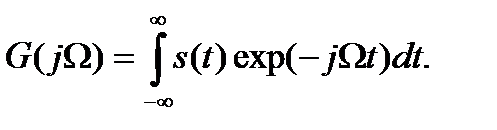 (3.4)
(3.4)
Таким образом, формулы (3.3) и (3.4) называются соответственно обратным и прямым преобразованиями Фурье Они показывают взаимосвязь между сигналом s (t) и его комплексной спектральной плотностью G (j Ω).
Для одиночного прямоугольного импульса с амплитудой А и длительностью t на рис. 3.4 получим спектр S (j Ω) на рис. 3.5:
 .
.
Это выражение с учетом формулы Эйлера  можно переписать в виде
можно переписать в виде
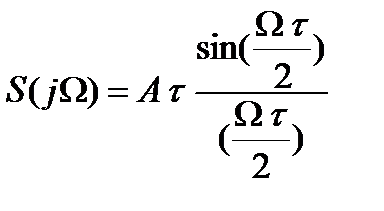 . (3.5)
. (3.5)
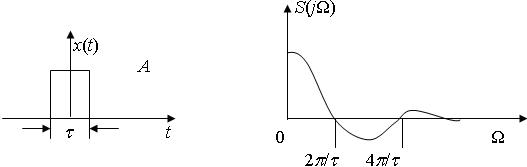
Рис. 3.4. Одиночный прямоугольный Рис. 3.5. Спектр
импульс прямоугольного импульса
Спектр непериодического сигнала сплошной, бесконечный, ширина спектра определяется длительностью сигнала и, приближённо, равна Δ F э ≈2p/t.
3.3. Основные свойства преобразования Фурье:
Свойствами преобразований Фурье определяется взаимное соответствие трансформации сигналов и их спектров.
1. Линейность. Преобразование Фурье относится к числу линейных интегральных операций, т.е. спектр суммы сигналов равен сумме спектров этих сигналов.
 (3.6)
(3.6)
Пример суммирования сигналов и его отображения в суммирования спектров приведен на рис. 3.6:
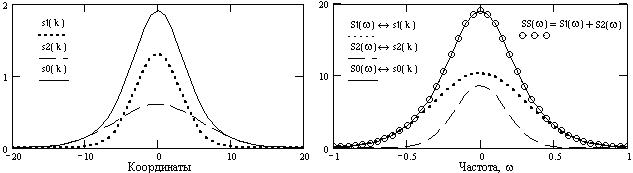
Рис. 3.6. Сигналы и их спектры. s 0(k) = s 1(k)+ s 2(k) S 1(ω)+ S 2(ω) = S 0(ω).
2. Свойства четности преобразования определяются косинусными (четными, действительными) и синусными (нечетными, мнимыми) частями разложения и подобием прямого и обратного преобразований.
На рис. 3.7. приведены примеры, поясняющие свойства четности преобразования. Сигнал s 1(k) является четным, s 1(k) = s 1(- k), и имеет только вещественный четный спектр (мнимая часть спектральной функции представлена нулевыми значениями). Сигнал s 2(k)= - s 2(- k) нечетный и имеет мнимый нечетный спектр, а нулевыми значениями представлена его действительная часть. Сигнал s 3(k) образован суммой сигналов s 1(k) и s 2(k). Соответственно, спектральная функция сигнала представлена и действительной четной частью (принадлежащей s 1(k)), и мнимой нечетной частью (принадлежащей s 2(k)). При обратном преобразовании Фурье раздельно действительной и мнимой части спектра S 3(ω), равно как и любых других комплексных спектров, будут раздельно восстановлены четная и нечетная части исходного сигнала.
Заметим, что произвольный исходный сигнал может быть задан в одностороннем варианте (в интервале 0 – Т), но четная и нечетная части этого сигнала занимают интервал от - Т до Т, при этом на левой половине числовой оси (от - Т до 0) эти два сигнала компенсируют друг друга, давая нулевые значения.
Сигнал s (t), спектр S (ω). При этом если:
s (t) – четный, то S (ω) – вещественный, четный;
s (t) – нечетный, то S (ω) – мнимый, нечетный
s (t) – произвольный, то S (ω) – действительная часть – четная,
а мнимая часть – нечетная.

Рис. 3.7. Свойства четности преобразования
3. Изменение аргумента функции (сжатие или расширение сигнала) приводит к обратному изменению аргумента ее Фурье-образа и обратно пропорциональному изменению его модуля. Действительно, если s (t) S (ω), то при изменении длительности сигнала с сохранением его формы (растяжении сигнала по временной оси), т.е. для сигнала с новым аргументом s (x) = s (a ∙ t) при x = a ∙ t, получаем:
 (3.7')
(3.7')
Выражение (3.7') действительно при а > 0. При а < 0 происходит зеркальный поворот сигнала относительно вертикальной оси, а замена переменной t = x / a вызывает перестановку пределов интегрирования и, соответственно, изменение знака спектра:
s (a ∙t) -(1/ a) S (ω / a). (3.7'')
Обобщенная формула изменения аргумента:
s (a ∙ t) -(1/| a |) S (ω / a), a ≠ 0 (3.7)
Если под аргументом функции и ее спектра понимать определенные физические единицы, например, время - частота, то отсюда следует: чем короче по своей длительности сигнал, тем шире по частоте его спектр, и наоборот. Это можно наглядно видеть на рис. 3.6. для сигналов s 1(k) и s 2(k) и их спектров S 1(ω) и S 2(ω).
От изменения аргумента функций следует отличать изменение масштаба представления функций. Изменение масштаба аргументов изменяет только оцифровку числовых осей отображения сигналов и их спектров, но не изменяет самих сигналов и спектров. Так, при масштабе оси времен t = 1 секунда, масштаб оси частот f = 1/ t = 1 герц, а при t = 1 мксек f = 1/ t = 1 МГц (t = a ∙ t, f = 1/ a ∙ t, a = 10-6).
4. Теорема запаздывания. Запаздывание (сдвиг, смещение) сигнала по аргументу функции на интервал t o приводит к изменению фазочастотной функции спектра (фазового угла всех гармоник) на величину - ωt o без изменения модуля (амплитудной функции) спектра. Применяя замену переменной t - t o = x, получаем:
 (3.8)
(3.8)
Совершенно очевидно, что амплитуды гармоник сигнала при его сдвиге изменяться не должны. С учетом того, что |exp(- jωt o)| = 1, это следует и из (3.8):
| S (ω) exp(- jωt o)| = | S (ω)|.
Фазовый спектр сдвигается на - ωt o с линейной зависимостью от частоты:
S (ω) exp(- jωt o) = R (ω) exp[ j (j (ω)] exp(- jωt o) = R (ω) exp[ j (j (ω) - ωt o)]. (3.9)

Рис. 3.8. Изменение спектра сигнала при его сдвиге.
Пример двух одинаковых сигналов, сдвинутых относительно друг друга на t o = 1, и соответствующих данным сигналам спектров приведен на рис. 3.8.
5. Преобразование производной (дифференцирование сигнала):
 (3.10)
(3.10)
Таким образом, дифференцирование сигнала отображается в спектральной области простым умножением спектра сигнала на оператор дифференцирования сигнала в частотной области jω, что эквивалентно дифференцированию каждой гармоники спектра. Умножение на jω приводит к обогащению спектра производной сигнала высокочастотными составляющими (по сравнению с исходным сигналом) и уничтожает составляющие с нулевой частотой.
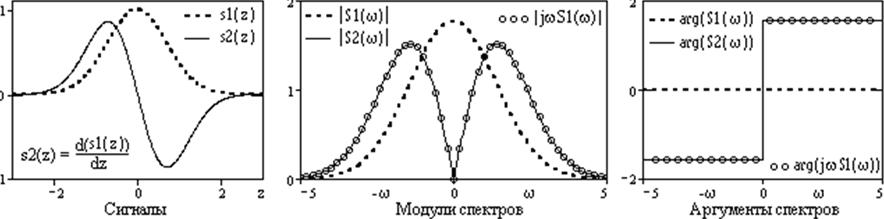
Рис. 3.9. Спектры сигнала и его производной
Пример сигнала, его производной и соответствующих им спектров приведен на рис. 3.9. По изменению аргумента спектра (для четного исходного сигнала он был нулевым) можно видеть, что для всех гармоник спектра появляется сдвиг фаз на π /2 (900) для положительных частот, и на - π /2 (-900) для отрицательных частот.
В общем случае, для кратных производных:
dn [ y (t)]/ dtn = (jω) n Y (ω). (3.11)
6. Преобразование интеграла сигнала в частотной области при известном спектре сигнала может быть получено из следующих простых соображений. Если имеет место s (t) = d [ y (t)]/ dtjω Y (ω) = S (ω), то должна выполняться и обратная операция:  . Отсюда следует:
. Отсюда следует:
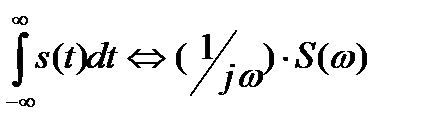 (3.12)
(3.12)
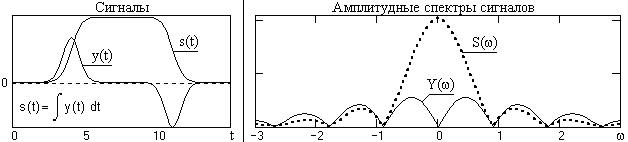
Рис. 3.10. Сигналы и амплитудные спектры сигналов
Оператор интегрирования в частотной области(1/ jω) при ω > 1 ослабляет в амплитудном спектре высокие частоты и при ω < 1 усиливает низкие. Фазовый спектр сигнала смещается на -900 для положительных частот и на 900 для отрицательных. Пример модуля спектра сигнала и его интегральной функции приведены на рис. 3.10.
Формула (3.12) справедлива для сигналов с нулевой постоянной составляющей. При интегрировании сигналов с определенным значением постоянной составляющей С = const в правой части выражения (3.12) появляется дополнительное слагаемое преобразования Фурье постоянной составляющей C, которое представляет собой, как будет показано ниже, дельта-функцию на нулевой частоте с весовым коэффициентом, равным значению С:
y (t) Y (ω) = (1/ jω) S (ω) + C · d (ω o).
7. Преобразование свертки сигналов y (t) = s (t) * h (t):

 .
.
По теореме запаздывания (3.8):
 .
.
Отсюда: 
s (t) * h (t) S (ω) ∙ H (ω). (3.13)
Пример выполнения свертки в частотной области приведен на рис. 3.11.

Рис. 3.11. Сигналы и амплитудные спектры сигналов
Отметим, что частотное представление H (ω) импульсного отклика h (t) линейной системы (или соответствующей линейной операции) имеет смысл частотной передаточной функции системы и позволяет определить сигнал на выходе системы (в частотной форме представления) при задании произвольного сигнала (в частотной форме) на ее входе. По существу, функция H (ω) представляет собой распределение по частоте коэффициента пропускания частотных составляющих сигнала с входа на выход системы (операции).
Таким образом, свертка функций в координатной форме отображается в частотном представлении произведением Фурье-образов этих функций.
Это положение имеет фундаментальное значение в практике обработки данных.
Любая линейная система обработки данных (информационных сигналов) реализует определенную операцию трансформации сигнала, т.е. выполняет операцию свертки входного сигнала s (t) с оператором системы h (t). С использованием преобразования свертки эта операция может производиться как с динамической, так и с частотной формой представления сигналов. При этом обработка данных, представленных в цифровой форме, производится, как правило, в частотной области, т.к. может быть на несколько порядков выше по производительности, чем во временной области. Она представляет собой последовательность следующих операций.
1) Перевод сигнала в частотную область: s (t) S (ω).
2) Умножение спектра сигнала на передаточную функцию системы:
Y (ω) = H (ω)· S (ω).
Передаточная функция системы определяется аналогичным преобразованием h (τ) H (ω) или задается непосредственно в частотном представлении, что позволяет задавать передаточные функции сколь угодно сложной формы, в том числе с разрывами и скачками, для которых во временной области потребуются операторы h (τ) с бесконечной импульсной характеристикой.
3) Перевод спектра обработанного сигнала во временную область:
Y (ω) y (t).
8. Преобразование произведения сигналов y (t) = s (t)· h (t):
Произведение функций в координатной форме отображается в частотном представлении сверткой Фурье-образов этих функций, с нормировочным множителем (1/2π), учитывающим несимметричность прямого и обратного преобразования Фурье функций s (t) и h (t) при использовании угловых частот.
 (3.14)
(3.14)
9. Спектральная плотность (прямое преобразование Фурье)
a) гармонической функции s (t) = cos(ω 0 t)
 ;
;
б) радиоимпульса (свойство смещения спектра) позволяет рассчитать спектральную плотность сигнала s (t), умноженного на гармоническое колебание s 1(t) = s (t)cos(ω 0 t + φ 0).
 ,
,
где GA (j Ω) – спектральная плотность огибающей A (t).
Следовательно возникает расщепление спектра G (j Ω) на две части максимумы которых возникают на частотах (+ ω 0) и (– ω 0).
в) δ-функции s (t) = δ(t):
G (j Ω) = 1
Спектры мощности.
Временная функция мощности сигнала в общей форме определяется выражением:
w (t) = s (t) s *(t) = | s (t)|2.
Спектральная плотность мощности, соответственно, равна преобразованию Фурье произведения s (t)· s *(t), которое отобразится в спектральном представлении сверткой Фурье-образов этих функций:
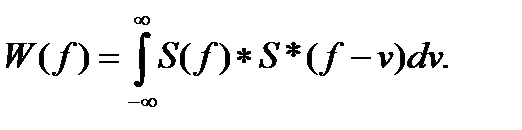 (3.15)
(3.15)
Но для всех текущих значений частоты f интеграл в правой части этого выражения равен произведению S (f)· S *(f), так как для всех значений сдвига v ≠ 0 в силу ортогональности гармоник S (f) и S *(f - v) значения их произведения равны нулю. Отсюда:
W (f) = S (f) * S *(f) = | S (f)|2. (3.16)
Спектр мощности – вещественная неотрицательная четная функция, которую очень часто называют энергетическим спектром. Спектр мощности, как квадрат модуля спектра сигнала, не содержит фазовой информации о частотных составляющих, а, следовательно, восстановление сигнала по спектру мощности невозможно. Это означает также, что сигналы с различными фазовыми характеристиками могут иметь одинаковые спектры мощности. В частности, сдвиг сигнала не отражается на его спектре мощности.
Для функций мощности взаимодействия сигналов в частотной области соответственно имеем частотные спектры мощности взаимодействия сигналов:
Wxy (f) = X (f) Y *(f),
Wyx (f) = Y (f) X *(f),
Wx y(f) = W * yx (f).
Функции мощности взаимодействия сигналов комплексные, даже если обе функции x (t) и y (t) вещественны, при этом Re[ Wxy (f)] – четная функция, а Im[ Wxy (f)] – нечетная. Отсюда полная энергия взаимодействия сигналов при интегрировании функций мощности взаимодействия определяется только реальной частью спектра:
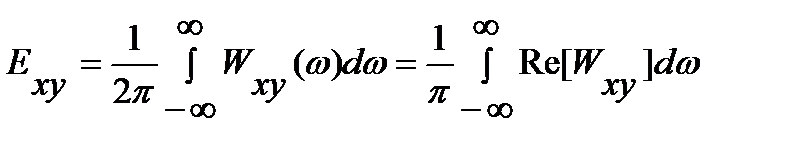 ,
,
и всегда является вещественным числом.
11. Равенство Парсеваля. Полная энергия спектра сигнала:
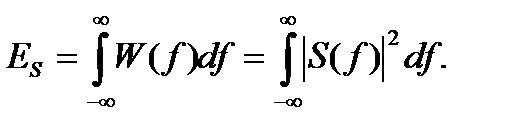 (3.17)
(3.17)
Так как координатное и частотное представление по существу только разные математические отображения одного и того же сигнала, то равной должна быть и энергия сигнала в двух представлениях, откуда следует равенство Парсеваля:
 ,
,
т.е. энергия сигнала равна интегралу модуля его частотного спектра – сумме энергий всех частотных составляющих сигнала. Аналогично для энергии взаимодействия сигналов:

Из равенства Парсеваля следует инвариантность скалярного произведения сигналов и нормы относительно преобразования Фурье:
(x (t), y (t)) = (X (f), Y (f)), || x (t)||2 = || X (f)||2.
Не следует забывать, что при представлении спектров в круговых частотах (по ω) в правой части приведенных равенств должен стоять множитель 1/2 π.




 . (3.3)
. (3.3)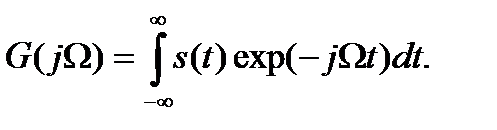 (3.4)
(3.4) .
. можно переписать в виде
можно переписать в виде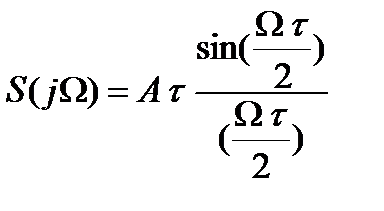 . (3.5)
. (3.5)
 (3.6)
(3.6)

 (3.7')
(3.7') (3.8)
(3.8)
 (3.10)
(3.10)
 . Отсюда следует:
. Отсюда следует: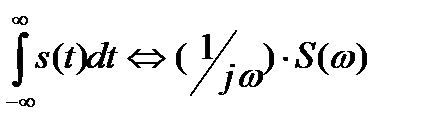 (3.12)
(3.12)

 .
. .
.

 (3.14)
(3.14) ;
; ,
,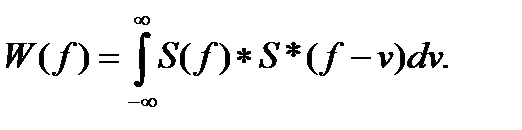 (3.15)
(3.15)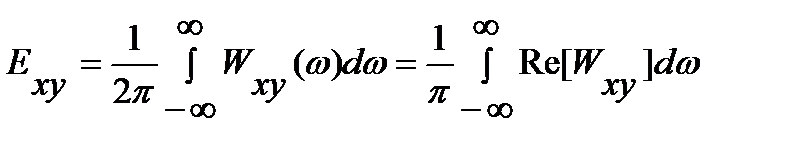 ,
,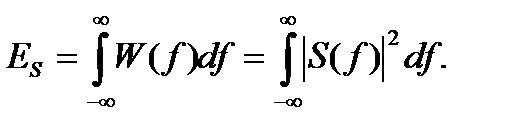 (3.17)
(3.17) ,
,



