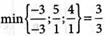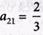АНАЛИТИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Основным аналитическим методом решения задач линейного программирования является симплексный метод. Так называется метод последовательного решения задачи или улучшения плана.
Симплексный метод заключается в определении опорного решения (плана) среди решений системы линейных ограничений-неравенств, затем поэтапным переходом к оптимальному решению.
Вычислительным процессом симплексного метода являются модифицированные жордановы исключения, позволяющие решать задачу линейного программирования в табличной форме.
Пусть основная задача линейного программирования записана в виде:
Z = c1x1 + c2x2 + …+ cnxn → max (4.1)
ai1x1 + ai2x2 + … + ainxn ≤ bi, i = (1,m) (4.2)
где m > n и xk ≥ 0, k = (1,n) (4.3)
Введем зависимые переменные согласно условиям yi ≥ 0 и ограничения (4.2) перепишем в виде:
yi = - ai1x1 – ai2x2 - … - ainxn + bi ≥ 0, i = (1,m) (4.4)
Исходную задачу (4.1) и (4.4) представим в табличной форме (4.5):
 (4.5)
(4.5)
Один шаг модифицированного исключения с разрешающим элементом ars означает переход к новой таблице (4.6), которая получается из табл. (4.5) по правилам:
1. зависимая переменная уr и независимая xs меняются местами, т.е. превращаются зависимые переменные в независимые;
2. разрешающий элемент ars заменяем на обратную величину (1/ ars);
3. остальные (кроме разрешающего) элементы разрешающей строки делятся на разрешающий элемент ars;
4. остальные элементы разрешающего столбца делятся на отрицательное значение разрешающего элемента, т.е. (-ars);
5. элементы bjk (i ≠r,s≠ к), т.е. элементы матрицы (4.6), не принадлежащие разрешающим столбцу и строке, вычисляются по формуле:

или по правилу так называемого «прямоугольника»


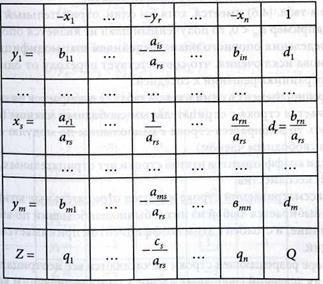
(4.6)
Решение задачи линейного программирования состоит из двух этапов:
1. нахождение опорного решения, условием которого является отсутствие отрицательных свободных членов, т.е. чтобы все элементы табл. (4.6), расположенные в столбце под 1 были неотрицательными.
2. Определение оптимального решения (плана), задачи, т.е. отыскание экстремальных значений целевой функции (max или min).
Условием оптимальности при определении максимального значения целевой функции является отсутствие отрицательных коэффициентов в Z — строке, табл. (4.6), кроме свободного члена Q.
Пример 4.1
 (4.7)
(4.7)
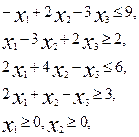 (4.8)
(4.8)
Найти опорное решение задачи линейного программирования:
Решение
1. Вводим зависимые переменные  и перепишем ограничения (4.8) в виде:
и перепишем ограничения (4.8) в виде:
 (4.9)
(4.9)
Целевую функцию (4.7) запишем в виде: Z = - (-4х1 + 2х2 - 3 х3) + 5.
2. Составляем симплексную табл. (4.10):
 (4.10)
(4.10)
Исходное решение не является опорным, так как в столбце свободных членов имеется два отрицательных элемента (-2 во второй строке и -3 в четвертой строке) в табл. 4.10.

3. Так как по условию задачи на переменную х3 ограничений на знак нет, то ее можно исключить из таблицы. Исключаем свободную переменную лг3, выполняя шаг модифицированного жорданова исключения с разрешающим элементом а43 = 1 для табл. (4.10), причем ограничений на выбор разрешающего элемента нет. Этот элемент выбираем в столбце под свободной переменной и отмечаем его квадратиком.
Из табл. (4.11) выписываем выражение для х3
(4.11)
x3 = 2x1 + x2 – y4 – 3 (4.12)
и вычеркиваем четвертую строку в этой таблице, записывая таблицу в виде:
(4.13)
4. Отыскиваем опорное решение, исключая отрицательный свободный член в табл. (4.13). Выполняем шаг модифицированного жорданова исключения с разрешающим элементом ars. Для выбора разрешающего элемента поступаем следующим образом: во второй строке отрицательный свободный член равен -8, а коэффициент в первом столбце равен -5 и принимаем его за разрешающий столбец. В качестве
разрешающей строки выбирали минимальное отношение из неотрицательных отношений свободных членов с соответствующим коэффициентом первого столбца, т.е.

Меньшее из них  , но в случае вырождения следует разрешающим элементом принимать число в знаменателе, если оно положительное. Следовательно, выбираем
, но в случае вырождения следует разрешающим элементом принимать число в знаменателе, если оно положительное. Следовательно, выбираем  и проведем шаг модифицированного жорданова исключения, который приводит к решению задачи в виде табл. (4.14).
и проведем шаг модифицированного жорданова исключения, который приводит к решению задачи в виде табл. (4.14).
 (4.14)
(4.14)
Выписываем решения задачи из табл. (4.14). Переменные, расположенные на верху таблицы, равны нулю, т.е. у2 = х2 = у4 = 0, а значения переменных; расположенных в левом столбце таблицы, равны  ,
,  ,
, 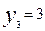 , Z = 12.
, Z = 12.
. Значение свободной х3 определяем из соотношения (4.12):

Итак, план (решение) задачи является опорным, так как все свободные члены табл. (4.12) положительны (элементы столбца, расположенные под 1).
Проверка значения целевой функции:

Ответ: 
Пример 4.2
Для заданной целевой функции

(4.15)
при линейных ограничениях:

(4.16)
и условиях:

(4.17)
определить опорное решение.
Решение
1. Вводим зависимые переменные  и запишем условие задачи (4.15)-(4.17) в виде
и запишем условие задачи (4.15)-(4.17) в виде
4.18)
 (4.19)
(4.19)
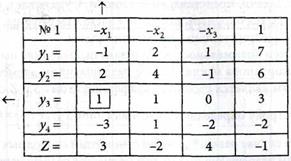
2. Составляем симплексную таблицу, размещая на верху таблицы независимые переменные «-хк», а в левом столбце — зависимые переменные yi и целевую функцию Z. Коэффициенты при переменных находятся в соответствующих строках и столбцах таблицы. Свободные члены уравнений записываем в последнем столбце под «1». Табл. № 1 имеет вид:

Номера таблицы будем указывать в левом верхнем углу симплексной таблицы. Исходное решение задачи (первоначальный план) не является опорным, так как при  (все переменные, расположенные на верху таблицы, равны нулю)
(все переменные, расположенные на верху таблицы, равны нулю)  Значение
Значение 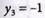 не удовлетворяет условию задачи.
не удовлетворяет условию задачи.
Исключаем свободную переменную х2, выполняя шаг модифицированного жорданова исключения с разрешающим элементом а32 = -2, (при этом ограничений на его выбор нет).
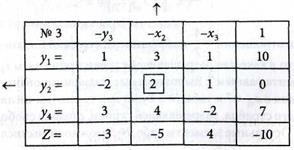
Получим табл. № 2:

Выписываем выражение для х2

и вычеркиваем третью строку в табл. № 2.
Решение задачи остается неопорным, так как в первой строке свободный член равен -1, а коэффициенты этой строки являются положительными. Следовательно, система ограничений несовместна.
Пример 4.3
Для реализации трех видов товаров предприятие располагает тремя видами ресурсов b1 = 180, b2 = 50 и b3 = 40. Для продажи первой группы товаров на одну тысячу рублей товарооборота расходуется ресурсов первого вида в количестве а11 = 3 единицы, ресурсов второго вида а21 = 2 единицы и третьего а31 = 2 единицы. Для продажи второй и третьей групп товаров на 1 тысячу рублей товарооборота расходуется соответственно:
a2l = 6 единиц, al3 = 4 единицы, а22 = 1 единицу, a23 = 2 единицы, а32 =3 единицы, а33 = 1 единицу.
Прибыль, полученная от продажи трех групп товаров на единицу товарооборота, составляет: с1 = 6, с2 = 5 и с3 = 5.
Определить максимальную прибыль предприятия.
Математическая модель задачи имеет вид:
 (4.20)
(4.20)
при ограничениях-неравенствах:
 (4.21)
(4.21)
и условиях:
 (4.22)
(4.22)
Решение
1. Вводим зависимые переменные yi ≥ 0 удовлетворяющие условиям: 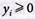
и перепишем ограничения (4.16) и целевую функцию Z (4.20) в виде:
(4.23)

(4.24)
2. Составляем симплексную табл. №1, включая в нее независимые переменные -x1 -x2,,-х3, на верху таблицы, зависимые переменные y1,y2,у3 и целевую функцию Z, записывая в левом столбце таблицы с соответствующими знаками у коэффициентов - aik. Ограничения на знак в таблицу не включаем.

Первоначальный план (исходное решение) является опорным, так как при х1 = х2 = х3 = 0 (все переменные, расположенные на верху таблицы, равны нулю) и зависимые переменные у1 = 180, у2 = 50, уъ = 40 удовлетворяют условиям уi ≥ 0.
3. Определяем оптимальное (максимальное) решение задачи линейного программирования. Находим разрешающий элемент ars. В качестве разрешающего выбираем столбец, содержащий наибольший отрицательный по абсолютной величине коэффициент Z-строки, равный «-6». В табл. № 1 указано вертикальной стрелкой. Разрешающую строку определяем из условия min

Такой строкой будет третья (указана горизонтальной стрелкой). Следовательно ars = а31 = 2.
Выполним шаг модифицированного жорданова исключения с разрешающим элементом а31 = 2, отмечено квадратиком. Получим табл. №2 в виде:

Разрешающий элемент а31 = 2, заменяем обратной величиной, равной 1/2. Все остальные элементы разрешающего столбца делим на «-2», получаем

Остальные элементы разрешающей строки делим на 2 и получаем:

Все элементы табл. №2 получаем, вычисляя по правилу «прямоугольника».
Вычисления элементов таблицы запишем по строкам:

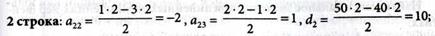


Решение, представленное табл. № 2, не является оптимальным, так как в Z-строке имеется отрицательный коэффициент, равный -2. Выполним шаг модифицированного жорданова исключения с разрешающим элементом а23 = 1 (третий столбец — разрешающий, а строка определена из условия min
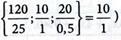
и получим табл. № 3 в виде:

Вычисления для заполнения табл. № 3 выполняем, начиная с разрешающих строки и столбца, а затем определяем элементы столбца свободных членов и Z-строки. Так как свободные члены и коэффициенты Z-строки неотрицательны, то решение является оптимальным. Остальные элементы симплекс-таблицы можно не вычислять.
Решение задачи выписываем из табл. № 3:
у3 = х2 = у2 = 0, так как все переменные, расположенные на верху таблицы равны нулю. Тогда переменные, находящиеся в левом столбце таблицы равны соответствующим значениям свободных членов (элементы в столбце под «1»), то есть

Проверка.
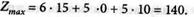
Ответ:

Пример 4.4
Для заданной целевой линейной функции
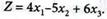
(4.25)
Найти максимальное значение при линейных ограничениях-неравенствах:

(4.26)
и условиях:

(4.27)
Решение
1. Введем зависимые переменные, удовлетворяющие условиям уi > 0, и перепишем систему ограничений (4.26) и целевую функцию (4.25) в виде:

(4.28)

(4.29)
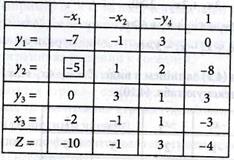
2. Составляем симплексную табл. № 1, включая в нее зависимые yj независимые переменные -хк (4.28) и целевую функцию Z (4.29). Ограничения на знак переменных хк в таблицу не включаем. Номера таблиц будем указывать в левом верхнем углу:

Исходный (первоначальный) план является неопорным, так как в третьей строке уз = -5 (свободный член, т.е. элемент табл. № 1 в столбце под 1 величина отрицательная).

| Полученное решение представлено табл. № 2:
|

3. Определяем опорное решение, выполняя шаг модифицированного жорданова исключения с разрешающим элементом а33 = -1 выбранным в соответствии с правилами, изложенными выше, т.е. в качестве разрешающего столбца берем коэффициент в третьей строке (свободный член равен -5) под переменной х3, а разрешающей будет строка с наименьшим положительным отношением свободных членов к соответствующим коэффициентам разрешающего столбца, т.е.
Решение задачи, представленное табл. № 2, показывает, что план является опорным, но неоптимальным, так как в Z-строке все коэффициенты отрицательные.
4. Определяем оптимальное решение, выполняя шаг модифицированного жорданова исключения с разрешающим элементом а21 = 1. В качестве разрешающего столбца берем наибольший по модулю отрицательный коэффициент — 16, т.е. столбец под переменной х1 (отмеченный вертикальной стрелкой), а разрешающей будет строка с единственным положительным коэффициентом равным 1. Следовательно, a21 = 1, а решение будет представлено табл. № 3:

Решение задачи, представленное табл. № 3, является оптимальным, так как все коэффициенты Z-строки — положительные величины. Выписываем решения задачи из табл. № 3:


Проверка зависимых переменных и целевой функции:
Пример 4.5
Определить значения независимых переменных хк, доставляющие целевой функции максимальное значение

(4.30)
удовлетворяющие линейным ограничениям-неравенствам:

(4.31)
 и условиям:
и условиям:
(4.32)
Решение
1. Введем зависимые переменные yt > 0 и ограничения (4.31) перепишем в виде:
2. Составляем симплексную табл. № 1, включая в нее зависимые, независимые переменные и целевую функцию (4.30):
Исключаем из табл. № 1 свободную независимую переменную
xv выбирая в качестве разрешающего элемента любой коэффициент в этом столбце (под переменной
хх ), так как согласно правилу выбора разрешающего элемента при исключении свободной переменной ограничений на выбор его нет.
Разрешающий элемент отмечен квадратиком, а соответствующие разрешающие строка и столбец указаны стрелками. Выполним шаг модифицированного жорданова исключения с разрешающим элементом а31 = 1 и получаем табл. № 2:
В табл. № 2 вписываем значение для х1 и вычеркиваем третью строку
(4.33)
Перепишем табл. № 3 в виде:
Решение задачи, представленное табл. № 3, указывает, что полученный план является опорным, так как все элементы столбца, расположенные под 1, — неотрицательны, но неоптимальны.
Определяем оптимальное решение задачи, выполняя шаг модифицированного жорданова исключения с разрешающим элементом а22 = 2. Разрешающим является столбец с коэффициентом -5 в Z-строке, а разрешающую строку определяем из условия
Так как в случае равенства нулю отношений свободных членов к коэффициентам разрешающего столбца в качестве разрешающего элемента берем коэффициент с положительным знаком, получаем табл. № 4:

Полученное решение не является оптимальным, так как в Z-строке имеется отрицательный коэффициент, равный -8. Принимаем столбец с этим коэффициентом в качестве разрешающего, а строку определяем из условия:


Так как в отношении коэффициент, стоящий в знаменателе, отрицательный, то в качестве разрешающей строки принимаем третью строку с коэффициента равным 7. Выполним шаг модифицированного жорданова исключения с а31 = 7 и табл. № 5 будет иметь вид (вычисляем элементы разрешающего столбца, разрешающей строки, столбца свободных членов и Z-строки. Остальные элементы табл. № 5 можно не вычислять).

План, представленный табл. № 5, является оптимальным. Выписываем решения задачи:
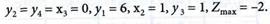
Вычисляем значение свободной переменной х1 на основании (4.33):

Вычисляем значения зависимых переменных у{ и целевой функции, подставляя найденные значения в (4.30) и (4.31).

Пример 4.6
Для заданной целевой функции найти максимальное значение:

| при линейных ограничениях-неравенствах
|
(4.34)

и условиях:
(4.35)
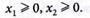
(4.36)
Решение
1. Вводим зависимые переменные  и перепишем условие задачи (4.34)-(4.36) в виде:
и перепишем условие задачи (4.34)-(4.36) в виде:
(4.37)
 (4.38)
(4.38)
2. Составляем симплексную табл. № 1:

3. Исключаем свободную независимую переменную х3, выполняя шаг модифицированного жорданова исключения с разрешающим элементом а43 = 1. Получаем табл. № 2:

Выписываем значение переменной х3:
(4.39)

и вычеркиваем четвертую строку в табл. № 2.
Получаем табл. № 3 в виде:
Так как в табл. № 3 в столбце свободных членов два отрицательных элемента -5 и -10, то план неопорный. В качестве разрешающего принимаем 1 столбец, так как в третьей строке находится элемент с наибольшим отрицательным по модулю значением -10 и коэффициент -8 расположен в этом столбце, а разрешающую строку определяем из условия:

Следовательно, выполним шаг модифицированного жорданова исключения с разрешающим элементом а11 = -8, получим табл. № 4:

Решение, представленное табл. № 4, не является опорным, так как в столбце свободных членов имеется отрицательный элемент, равный -5. Выполнив шаг модифицированного жорданова исключения с разрешающим элементом а31 = -1, получим табл. № 5:

Решение, полученное в виде табл. № 5, является опорным, но не оптимальным, поскольку в Z-строке коэффициент равный – 15/8 в первом столбце отрицательный, но в этом столбце нет положительных коэффициентов. Следовательно, целевая функция ограничений на максимум не имеет.

Пример 4.7
Определить максимальное значение линейной целевой функции

(4.43)
при смешанных линейных ограничениях:

(4.44)
и условиях:
(4.45)

Решение

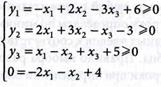
1. Вводим зависимые переменные 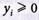 и перепишем условие задачи (4.43) и (4.44) в виде:
и перепишем условие задачи (4.43) и (4.44) в виде:
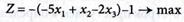
(4.47)
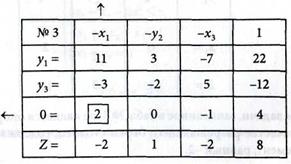
2. Запишем условие задачи (4.46) и (4.47) в табл. № 1, включая в нее зависимые, независимые переменные и целевую функцию:

3. Так как независимые переменные хк являются несвободными, то исключаем 0-строку.
В качестве разрешающего столбца принимаем любой положительный коэффициент 0-строки, например, a41 = 2. Разрешающую строку определим из условия:
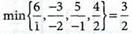
Следовательно, разрешающим элементом будет а21 = -2. Выполняя шаг модифицированного жорданова исключения с разрешающим элементом а21 = -2, отмеченный в табл. № 1 квадратиком. Получаем решение задачи в виде табл. № 2:
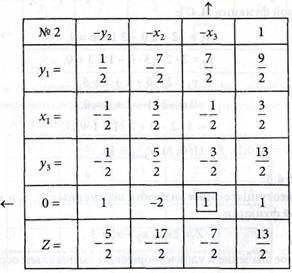
4. В табл. № 20 строка осталась. Исключаем ее, выполняя шаг модифицированного жорданова исключения с разрешающим элементом а43 = 1. Получаем табл. № 3 в виде:

Вычеркивая в табл. № 3 0-столбец, получаем решение опорное и оптимальное.
Выпишем решение задачи из табл. № 3 и проверим условия (4.46) и значение целевой функции (4.47):

Пример 4.8
Найти неотрицательные значения переменных x1,x2 и х3 доставляющие целевой функции
(4.48)
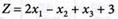
максимальное значение и удовлетворяющие смешанным ограничениям:
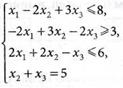
и условиям:
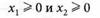
Решение
1. Перепишем ограничения (4.49) с учетом введенных переменных
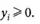

2. Составляем симплексную табл. № 1
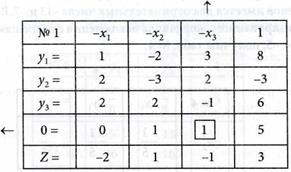
3. Исключаем свободную переменную х3 в табл. № 1, выполняя шаг модифицированного жорданова исключения с разрешающим элементом а43 = 1. Получим табл. № 2:

В табл. № 2 вычеркиваем 0-столбец, выписываем выражение для независимой переменной хъ
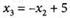
и вычеркиваем четвертую строку.
Получаем табл. № 3, уменьшенную на одну строку и один столбец:

4. Полученное решение не является опорным, так как в столбце свободных членов имеется два отрицательных числа -13 и -7. Выполним шаг модифицированного жорданова исключения с разрешающим элементом а12 = -5, получим табл. № 4:

5. Решение остается неопорным, поэтому выполним шаг модифицированного жорданова исключения с разрешающим элементом а22 = -1 в табл. № 5:

6. Полученное решение является опорным, но неоптимальным, поскольку в Z-строке первый коэффициент — отрицательный, равный - 6/5.Выполним шаг модифицированного жорданова исключения с разрешающим элементом  . Получим табл. № 6 в виде:
. Получим табл. № 6 в виде:
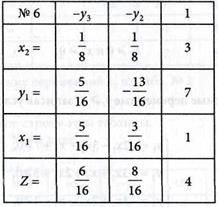
7. Из табл. № 6 выписываем решение задачи:
Проверка.

Пример 4.9
Найти максимальное значение линейной целевой функции
(4.51)

переменные которой удовлетворяют смешанным линейным ограничениям-неравенствам:
 (4.52)
(4.52)
и условиям:
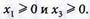 (4.53)
(4.53)
Решение
1. Вводим зависимые переменные 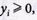 записав условие задачи (4.51)-(4.53) в виде:
записав условие задачи (4.51)-(4.53) в виде:
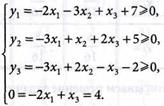
(4.54)
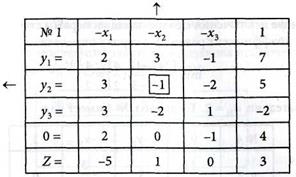
2. Составляем симплексную табл. № 1, представляя условие задачи (4.54) в табличной форме, включая в нее все переменные, 0-строку и целевую функцию Z:
3. Исключаем свободную независимую переменную
х2, выполняя шагмодифицированного жорданова исключения с разрешающим элементом
а22 = -1.
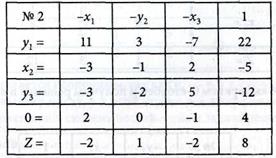
Полученная табл. № 2 имеет вид:
Запишем значение переменной
х2 из табл. № 2
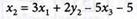
и вычеркнем вторую строку этой таблицы. Получаем табл. № 3 в виде:
4. Исключаем 0-строку в табл. № 3, выполняя шаг модифицированного жорданова исключения с разрешающим первым столбцом (в 0-строке этот коэффициент равен 2), а строку определяем из условия:
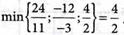
Следовательно, а31 = 2. Тогда табл. № 4 имеет вид:
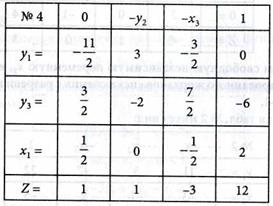
В табл. № 4 вычеркнем 0-столбец и получим решение в виде табл. № 5:

Решение задачи, записанное в табл. № 5, не является опорным, так как у3 = -6. В качестве разрешающего берем столбец, содержащий отрицательный элемент, равный -2.
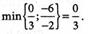 Разрешающую строку определяем из условия
Разрешающую строку определяем из условия
Выполнив шаг модифицированного жорданова исключения с разрешающим элементом а11 = 3, получим табл. № 6:
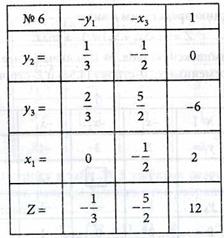
Решение является неопорным, так как у3 = -6, т.е. свободный член равен отрицательному числу, а в этой строке все коэффициенты положительны. Следовательно, система несовместна и задача решений не имеет.
Пример 4.10
Найти максимальное значение линейной целевой функции
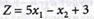
при смешанных линейных ограничениях:
(4.55)

и условиях:
(4.56)
(4.57)
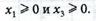
Решение
1. Введем зависимые переменные  и ограничения запишем в виде:
и ограничения запишем в виде:
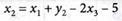
Выписываем выражение для переменной х2:
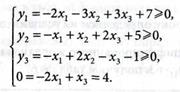 (4.58)
(4.58)
Целевую функцию представим в виде:

(4.59)
2. Составляем симплексную табл. № 1, включая в нее зависимые yi, независимые переменные хk, 0-строку (4.58) и Z-строку (4.59):

3. Исключаем свободную переменную х2, так как в условиях (4.55) ограничений на знак этой переменной нет. В качестве разрешающего выбираем любой элемент, стоящий в столбце под этой переменной табл. № 1. Пусть таким элементом будет а22 = -1, выделим его квадратиком. Выполним шаг модифицированного жорданова исключения с разрешающим элементом а22 = -1, получим табл. № 2:
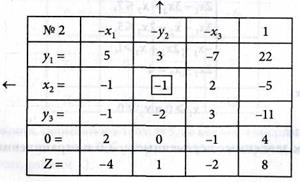
и вычеркиваем вторую строку табл. № 2. Получаем табл. № 3 в виде:
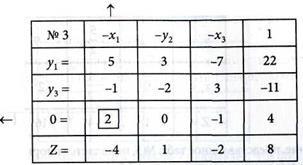
4. Исключаем 0-строку в табл. № 3, выбирая разрешающий столбец с коэффициентом, равным 2, в качестве разрешающей принимаем строку из условия:
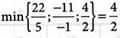
Выполним шаг модифицированного жорданова исключения с разрешающим элементом а31 = 2 и получим табл. № 4:
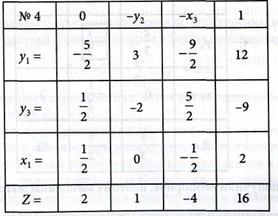
В табл. № 4 вычеркнем 0-столбец и запишем полученную таблицу в виде:
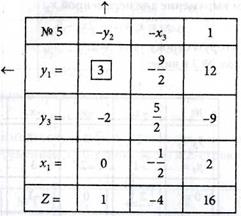
Решение, представленное табл. № 5, не является опорным, так как у3 = -9, что не удовлетворяет условию 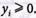 5. Определяем опорное решение задачи, выполняя шаг модифицированного жорданова исключения с разрешающим элементом а11 = 3. Получаем табл. № 6:
5. Определяем опорное решение задачи, выполняя шаг модифицированного жорданова исключения с разрешающим элементом а11 = 3. Получаем табл. № 6:
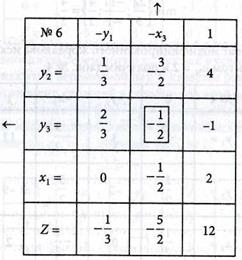
 Решение получили неопорное, поэтому выполним шаг модифицированного жорданова исключения с разрешающим элементом и получим табл. № 7:
Решение получили неопорное, поэтому выполним шаг модифицированного жорданова исключения с разрешающим элементом и получим табл. № 7:

 Полученное решение задачи в табл. № 7 указывает, что функция Z ограничений на максимум не имеет, так как в Z-строке имеется два отрицательных коэффициента и -5, а в соответствующих столбцах нет положительных элементов.
Полученное решение задачи в табл. № 7 указывает, что функция Z ограничений на максимум не имеет, так как в Z-строке имеется два отрицательных коэффициента и -5, а в соответствующих столбцах нет положительных элементов.

Пример 4.11
Определить минимальное значение целевой функции
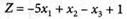 (4.60)
(4.60)
при линейных ограничениях-неравенствах
 (4.61)
(4.61)
и условиях
(4.62)
Решение
1. Целевую функцию (4.60) заменой Z1 = -Z сведем к определению максимального значения, т.е.

(4.63)
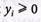 2. Введем зависимые переменные согласно условиям и запишем ограничения (4.61) в виде:
2. Введем зависимые переменные согласно условиям и запишем ограничения (4.61) в виде:
 (4.64)
(4.64)
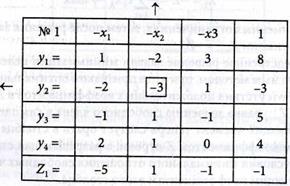
3. Составим симплексную табл. № 1, включая в нее независимые хк, зависимые переменные уi (4.64) и целевую функцию Z1 (4.64), т.е. условие исходной задачи запишем в табл. № 1:
Первоначальный план (решение) при
х1=, х2 = х3 = 0 имеет значение
y1 = 8, y2 = 3, у3 = 5, y4 = 4 и
Z1 = -1 не является опорным, так как
y2 = -3<0.
4. Определяем опорное решение задачи, выполняя шаг модифицированного жорданова исключения с разрешающим элементом а22 = -3. В качестве разрешающего столбца выбираем столбец с переменной х2 (во второй строке с отрицательным свободным членом равным -3 отыскиваем отрицательный наибольший по модулю коэффициент, равный -3). Разрешающую строку определяем из условия:
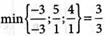
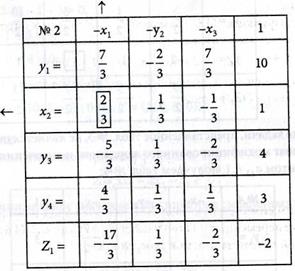
В табл. № 2 все свободные члены положительны, кроме свободного члена Z1 -строки. Следовательно, решение задачи является опорным.
5. Определяем оптимальное решение задачи, т.е. находим максимальное значение функции Z1 Так как в Z1 -строке имеется два отрицательных коэффициента -17/3 и -5/3, то в качестве разрешающего принимаем первый столбец с коэффициентом равным -17/3 (больший отрицательный по абсолютной величине). Разрешающую строку определяем из условия:
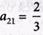

После шага модифицированного жорданова исключения с разрешающим элементом получаем табл. № 3:
Решение задачи, представленное табл. № 3, не является оптимальным. Выполняя шаг модифицированного жорданова исключения с разрешающим элементом а43 = 1, получаем табл. № 4:
Табл. № 4 заполняем в такой последовательности: выписываем разрешающие строку и столбец, а затем вычисляем значения свободных членов (столбец под 1) и коэффициентов
Z1 -строки. Так как условия опорности и оптимальности выполняются для рассматриваемой задачи, то нет необходимости в определении остальных элементов табл. № 4.
Выписываем решени



 (4.5)
(4.5)



 (4.7)
(4.7)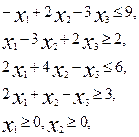 (4.8)
(4.8) и перепишем ограничения (4.8) в виде:
и перепишем ограничения (4.8) в виде: (4.9)
(4.9) (4.10)
(4.10)


 , но в случае вырождения следует разрешающим элементом принимать число в знаменателе, если оно положительное. Следовательно, выбираем
, но в случае вырождения следует разрешающим элементом принимать число в знаменателе, если оно положительное. Следовательно, выбираем  и проведем шаг модифицированного жорданова исключения, который приводит к решению задачи в виде табл. (4.14).
и проведем шаг модифицированного жорданова исключения, который приводит к решению задачи в виде табл. (4.14). (4.14)
(4.14) ,
,  ,
, 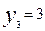 , Z = 12.
, Z = 12.





 (4.19)
(4.19)
 (все переменные, расположенные на верху таблицы, равны нулю)
(все переменные, расположенные на верху таблицы, равны нулю)  Значение
Значение 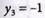 не удовлетворяет условию задачи.
не удовлетворяет условию задачи.

 (4.20)
(4.20) (4.21)
(4.21) (4.22)
(4.22)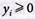







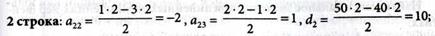


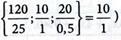


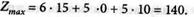

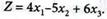













 и условиям:
и условиям:











 и перепишем условие задачи (4.34)-(4.36) в виде:
и перепишем условие задачи (4.34)-(4.36) в виде: (4.38)
(4.38)











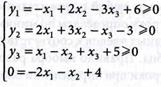
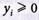 и перепишем условие задачи (4.43) и (4.44) в виде:
и перепишем условие задачи (4.43) и (4.44) в виде: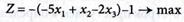

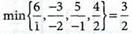



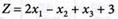
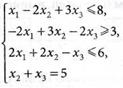
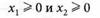
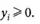



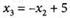



 . Получим табл. № 6 в виде:
. Получим табл. № 6 в виде:

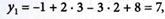


 (4.52)
(4.52)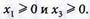 (4.53)
(4.53)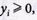 записав условие задачи (4.51)-(4.53) в виде:
записав условие задачи (4.51)-(4.53) в виде: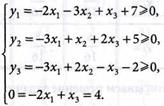
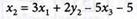
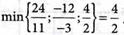


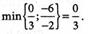 Разрешающую строку определяем из условия
Разрешающую строку определяем из условия
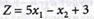

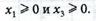
 и ограничения запишем в виде:
и ограничения запишем в виде: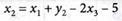
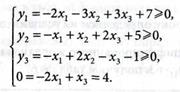 (4.58)
(4.58)



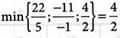


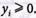 5. Определяем опорное решение задачи, выполняя шаг модифицированного жорданова исключения с разрешающим элементом а11 = 3. Получаем табл. № 6:
5. Определяем опорное решение задачи, выполняя шаг модифицированного жорданова исключения с разрешающим элементом а11 = 3. Получаем табл. № 6:
 Решение получили неопорное, поэтому выполним шаг модифицированного жорданова исключения с разрешающим элементом и получим табл. № 7:
Решение получили неопорное, поэтому выполним шаг модифицированного жорданова исключения с разрешающим элементом и получим табл. № 7:
 Полученное решение задачи в табл. № 7 указывает, что функция Z ограничений на максимум не имеет, так как в Z-строке имеется два отрицательных коэффициента и -5, а в соответствующих столбцах нет положительных элементов.
Полученное решение задачи в табл. № 7 указывает, что функция Z ограничений на максимум не имеет, так как в Z-строке имеется два отрицательных коэффициента и -5, а в соответствующих столбцах нет положительных элементов.
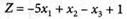 (4.60)
(4.60) (4.61)
(4.61)

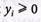 2. Введем зависимые переменные согласно условиям и запишем ограничения (4.61) в виде:
2. Введем зависимые переменные согласно условиям и запишем ограничения (4.61) в виде: (4.64)
(4.64)