8.1. Построение линии пересечения плоскостей общего положения.
8.2. Построение перпендикуляра к плоскости, проходящего через заданною точку.
8.3. Построение плоскости проходящей через заданную точку и перпендикулярно заданной прямой.
8.4. Построение прямой параллельной заданной плоскости.
8.5. Перпендикулярность и параллельность плоскостей.
8.6. Контрольные вопросы.
8.1. Построение линии пересечения плоскостей
общего положения
Две плоскости пересекаются друг с другом по прямой линии. Чтобы её построить, необходимо определить две точки, принадлежащие одновременно каждой из заданных плоскостей.
Для нахождения таких точек используется методика по определению точки встречи прямой с плоскостью, только при этом в качестве плоскости выбирается одна из заданных плоскостей, а в качестве прямой – прямая, принадлежащая другой плоскости.
Рассмотрим, как это делается, на следующем примере (рис. 71).
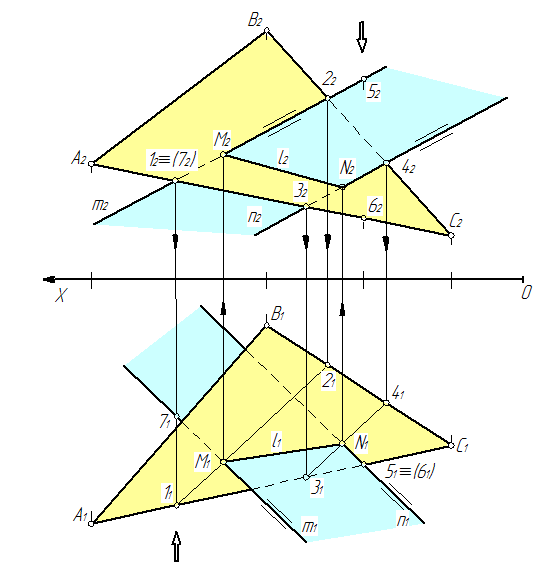
Рис. 71
Постановка задачи. Даны две плоскости общего положенияα, заданная треугольником ∆ АВС и β – двумя параллельными прямыми m и n.
Построить прямую l пересечения плоскостей α и β: l =α∩β и определить видимость плоскостей, ограниченных ∆ АВС и параллельными прямыми m и n.
Решение
1. Определяем первую точку М принадлежащею линии пересечения плоскостей l, как точку встречи прямой m с плоскость α: M ⊂ l; М = m ∩α.
2. Определяем вторую точку N принадлежащею линии пересечения плоскостей l, как точку встречи прямой n с плоскость α: N ⊂ l; N = n ∩α.
3. Через точки M и N проводим прямую пересечения плоскостей α и β: l =α∩β.
4. Устанавливаем видимость плоскостей α и βотносительно друг друга. Для горизонтальной плоскости проекций с помощью горизонтально конкурирующих точек5 и 6 (точка 6 лежит на стороне АС треугольника, а точка 5 – на прямой т). Для фронтальной плоскости проекций с помощью фронтально конкурирующих точек1 и 7 (точка 1 лежит на стороне АС треугольника, а точка 7 – на прямой п). Направление взгляда при определении видимости проекций конкурирующих точек на эпюре показана символами (⇧) и (⇩).
8.2. Построение перпендикуляра к плоскости,
проходящего через заданною точку
При решении геометрических задач часто бывает необходимо строить перпендикуляры к плоскости. Известно, что прямая перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым этой плоскости. В качестве этих двух пересекающихся прямых плоскости приходится использовать линии уровня плоскости, т.к. согласно теоремы о проецировании прямого угла, именно с этими прямыми сохраняется прямой угол на плоскостях проекциях. Условия перпендикулярности прямой и плоскости устанавливаются следующей теоремой.
Теорема. Для того, чтобы прямая была бы перпендикулярна к плоскости, необходимо и достаточно, чтобы горизонтальная проекция прямой была бы перпендикулярна к горизонтальной проекции горизонтали, а фронтальная проекция – перпендикулярна к фронтальной проекции фронтали этой плоскости.
Доказательство. Необходимость. Допустим, что прямая перпендикулярна к плоскости. Тогда она перпендикулярна к любым прямым этой плоскости, в том числе горизонталям и фронталям плоскости. Согласно теоремы о проецировании прямого угла, перпендикулярность прямой и горизонтали сохраняется на горизонтальной плоскости проекций, а перпендикулярность прямой и фронтали – на фронтальной плоскости проекций. Что и требовалось доказать.
Достаточность. Пусть на комплексном чертеже горизонтальная проекция прямой перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция прямой перпендикулярна к фронтальной проекции фронтали плоскости. Тогда в соответствии с теоремой о проецировании прямого угла, прямая в пространстве будет перпендикулярна к горизонтали и фронтали плоскости. А это значит, что прямая и плоскость взаимно перпендикулярны, что и требовалось доказать.
 Рис. 72
Рис. 72
|
Установленные теоремой признаки позволяют строить на комплексном чертеже прямые, перпендикулярные к плоскости.
Пример построения перпендикуляра к плоскости, проходящего через заданною точку (рис. 72).
Постановка задачи. Задана плоскостьα треугольником ∆ АВС и точка К.
Построить перпендикуляр т к плоскости α, проходящей через точку К.
Решение
1. В плоскости α проводится горизонталь h: h Ì αи h‖π 1.
2. Используя теорему о прямом угле строится первая проекция перпендикуляра m: m 1⊥ h 1 и К 1⊂ m 1.
3. В плоскости α проводится фронталь f: f Ì αи f‖ π2.
4. Используя теорему о прямом угле строится вторая проекция перпендикуляра m: m 2⊥ f 2 и К 2⊂ m 2.




 Рис. 72
Рис. 72



