

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...
Топ:
Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Интересное:
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Средства для ингаляционного наркоза: Наркоз наступает в результате вдыхания (ингаляции) средств, которое осуществляют или с помощью маски...
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Векторы. Определения. Операции
Вектор размера n – совокупность n чисел, заданных в определенном порядке.
Обозначается a = (a1, a2 , ….an).
Числа a1, a2 , ….an – компоненты вектора; n - его размерность.
Единичный вектор – все его компоненты равны 1. Обозначается 1
Нуль-вектор -все его компоненты равны 0. Обозначается 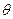 .
.
Противоположный вектор – a = (-a1, -a2 , ….-an). Очевидно a +(– a) =0
Основные операции:
1) Алгебраическая сумма двух векторов = алгебраической сумме их компонент
Умножение вектора на число – умножение каждой компоненты на это число
3) Скалярное произведение двух векторов – число, равное сумме произведений одноименных координат данных векторов
< a,b > = a1b1+a2b2+…anbn
Основные свойства скалярного произведения:
< a,b >=< b,a>; β< a, b >= < βa, b >; < a+ b, с>=< a,с>+ <b,с>; < a, a> >=0
Пример 1.
Пусть в производственное объединение входят две мебельные фабрики. Объем годового выпуска продукции каждой фабрики составляет:
| столы | стулья | кресла | кровати | вектор | ||
| a | |||||||
| b |
Матрицы. Определения. Операции
Матрица размера m x n – совокупностьчисел прямоугольной таблицы, состоящей из m строки n столбцов.
Обозначается
А= 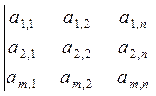 или А= (ai,j), i=1,2…m; j= 1,2…n
или А= (ai,j), i=1,2…m; j= 1,2…n
Числа ai,j – элементы матрицы, строки и столбцы – ее ряды.
Множество всех матриц размера m x n обозначается R m x n , А= R m x n
Основные определения и свойства матриц
1. Две матрицы А и В одного и того же размераравны, если равны соответствующие элементы, аi,j = bi,j
2. Вектор – столбец – матрица, состоящая из одного столбца
3. Вектор – строка – матрица, состоящая из одной строки
4. Нулевая матрица – все ее элементы =0; обозначатся Оmxn
|
|
5. Квадратная матрица – m=n (число строк равно числу столбцов)
6. Главная диагональ квадратной матрицы – элементы аi,i, лежащие на главной диагонали
7. Треугольная матрица – квадратная матрица, такая, что все ее элементы, расположенные по одну сторону от главной диагонали, равны нулю.
8. Единичная матрица Е – все элементы на главной диагонали аi,I =1, остальные элементы равны нулю.
9. Транспонированная матрица АТ – матрица, полученная из исходной матрицы А заменой строк на столбцы с сохранением порядка.
10. Сумма двух матриц C=A+B, А= ( аi,j) и В= ( bi,j ) одного и того же размера – матрица С = (сi,j) того же размера, элементы которой равны сумме соответствующих элементов исходных матриц –
сi,j= аi,j+ bi,j: C=A-B 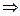 сi,j= аi,j- bi,j
сi,j= аi,j- bi,j
11. Произведение матрицы на число – все элементы исходной матрицы умножаются на это число. В=2А 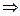 (bi,j =2ai,j). Очевидное следствие: общий множитель всех элементов матрицы можно выносить за знак матрицы
(bi,j =2ai,j). Очевидное следствие: общий множитель всех элементов матрицы можно выносить за знак матрицы
12. Произведение двух матриц А и В. Произведение имеет смысл, если
число столбцов первого сомножителя (например, А) совпадаетс числомстрок второго сомножителя (например, В). Пусть А= R m x n , В= R nхк, тогда С = АВ = R mxk.
Операция произведения двух матриц обладает следующими свойствами:
1) (AB)C= A(BC); α(AB)= (αA)B; (A+B)C=AC+BC; (AB)T = BTAT;
AE=EA=A
2) AB ≠BA в общем случае. Если AB = BA, то матрицы A и B называются перестановочными
3) Квадратную матрицу А можно возвести в квадрат, куб, в к –ую степень, получить Ак
4) А0 =Е
Пример 2. Предприятие выпускает продукцию трех видов Р1, Р2, Р3 и использует сырье двух типов S1 и S2.
Матрица А3х2 (технологическая). Показывает, сколько единиц сырья j-го типа расходуется на производство продукции i-го вида.
А= 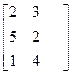
План выпуска продукции задан вектором- строкой С,
С= 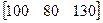
Стоимость единицы сырья каждого типа задается вектором – столбцом В
В= 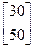
Матрица – строка затрат сырья может быть записана в матричном виде S = CA = 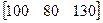
 =
= 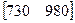
Тогда общая стоимость сырья
Q = SB = 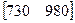
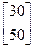 =730*30 + 980*50 = 70900 ден. ед.
=730*30 + 980*50 = 70900 ден. ед.
3. Применение матриц в задаче планирования производства
|
|
Предприятие выпускает n видов продукции, используя для этого m видов ресурсов. Известна технологическая матрица Аmxn затрат ресурсов на производство единицы каждого вида продукции. Элемент ai,j равен количеству ресурса i-го вида (i = 1..m), необходимого для производства продукта j-го вида (j=1..n). Каждый столбец матрицы А описывает некую технологию.
Известен вектор b (bi, i=1..m), имеющихся в распоряжении предприятия объемов ресурсов.
Известен также вектор C удельной прибыли предприятия. Элемент сj, j=1..n, - прибыль предприятия от реализации единицы продукции j–го вида.
Если обозначить через xj план производства продукции j–го вида, то производственная программа будет задаваться вектором Х
Тогда произведение АХ характеризует суммарные расходы ресурсов на реализацию плана. Очевидно, АХ ≤ b, т.е.
ai,1x1 + ai,2x2+…+ai,nxn ≤ bi i=1..m
Прибыль предприятия от реализации всей произведенной продукции равна
z= с1x1+ c2x2 +…+cnxn
Задача заключается в том, чтобы отыскать такой план производства, который обеспечит предприятию наибольшую прибыль
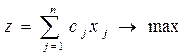
Поставленная выше задача является оптимизационной, решается методом линейного программирования. Метод был разработан лауреатом Нобелевской премии в области экономики, академиком Л. В. Конторовичем.
Обратная матрица
Пусть А – квадратная матица. Если существует матрица В, такая, что АВ=Е, то говорят, что В – обратная матрица.
Обратную матрицу обозначают А-1. Обратная матрица перестановочна с исходной, т.е А А-1 = А-1А = Е
Очевидно, (А А-1)-1 =А
Пример 1
Система линейных уравнений:
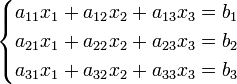
Определители:
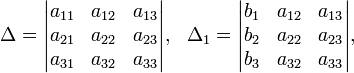
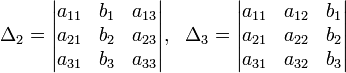
Решение:
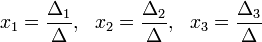
Пример 2
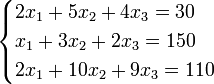
Определители:
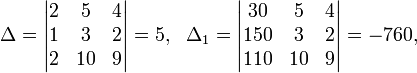
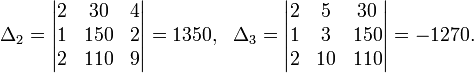
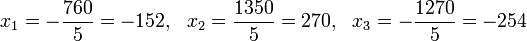


Пример 3 Вычисление коэффициентов обратной матрицы
Дана система линейных алгебраических уравнений. Решить методом обратной матрицы 
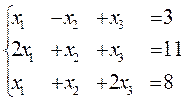

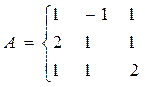
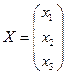
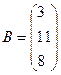
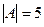
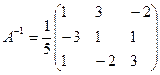
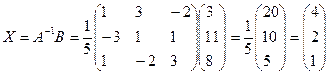
Векторы. Определения. Операции
Вектор размера n – совокупность n чисел, заданных в определенном порядке.
Обозначается a = (a1, a2 , ….an).
Числа a1, a2 , ….an – компоненты вектора; n - его размерность.
Единичный вектор – все его компоненты равны 1. Обозначается 1
Нуль-вектор -все его компоненты равны 0. Обозначается 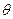 .
.
Противоположный вектор – a = (-a1, -a2 , ….-an). Очевидно a +(– a) =0
Основные операции:
1) Алгебраическая сумма двух векторов = алгебраической сумме их компонент
|
|
Умножение вектора на число – умножение каждой компоненты на это число
3) Скалярное произведение двух векторов – число, равное сумме произведений одноименных координат данных векторов
< a,b > = a1b1+a2b2+…anbn
Основные свойства скалярного произведения:
< a,b >=< b,a>; β< a, b >= < βa, b >; < a+ b, с>=< a,с>+ <b,с>; < a, a> >=0
Пример 1.
Пусть в производственное объединение входят две мебельные фабрики. Объем годового выпуска продукции каждой фабрики составляет:
| столы | стулья | кресла | кровати | вектор | ||
| a | |||||||
| b |
Матрицы. Определения. Операции
Матрица размера m x n – совокупностьчисел прямоугольной таблицы, состоящей из m строки n столбцов.
Обозначается
А= 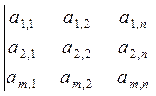 или А= (ai,j), i=1,2…m; j= 1,2…n
или А= (ai,j), i=1,2…m; j= 1,2…n
Числа ai,j – элементы матрицы, строки и столбцы – ее ряды.
Множество всех матриц размера m x n обозначается R m x n , А= R m x n
Основные определения и свойства матриц
1. Две матрицы А и В одного и того же размераравны, если равны соответствующие элементы, аi,j = bi,j
2. Вектор – столбец – матрица, состоящая из одного столбца
3. Вектор – строка – матрица, состоящая из одной строки
4. Нулевая матрица – все ее элементы =0; обозначатся Оmxn
5. Квадратная матрица – m=n (число строк равно числу столбцов)
6. Главная диагональ квадратной матрицы – элементы аi,i, лежащие на главной диагонали
7. Треугольная матрица – квадратная матрица, такая, что все ее элементы, расположенные по одну сторону от главной диагонали, равны нулю.
8. Единичная матрица Е – все элементы на главной диагонали аi,I =1, остальные элементы равны нулю.
9. Транспонированная матрица АТ – матрица, полученная из исходной матрицы А заменой строк на столбцы с сохранением порядка.
10. Сумма двух матриц C=A+B, А= ( аi,j) и В= ( bi,j ) одного и того же размера – матрица С = (сi,j) того же размера, элементы которой равны сумме соответствующих элементов исходных матриц –
сi,j= аi,j+ bi,j: C=A-B 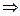 сi,j= аi,j- bi,j
сi,j= аi,j- bi,j
11. Произведение матрицы на число – все элементы исходной матрицы умножаются на это число. В=2А 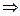 (bi,j =2ai,j). Очевидное следствие: общий множитель всех элементов матрицы можно выносить за знак матрицы
(bi,j =2ai,j). Очевидное следствие: общий множитель всех элементов матрицы можно выносить за знак матрицы
|
|
12. Произведение двух матриц А и В. Произведение имеет смысл, если
число столбцов первого сомножителя (например, А) совпадаетс числомстрок второго сомножителя (например, В). Пусть А= R m x n , В= R nхк, тогда С = АВ = R mxk.
Операция произведения двух матриц обладает следующими свойствами:
1) (AB)C= A(BC); α(AB)= (αA)B; (A+B)C=AC+BC; (AB)T = BTAT;
AE=EA=A
2) AB ≠BA в общем случае. Если AB = BA, то матрицы A и B называются перестановочными
3) Квадратную матрицу А можно возвести в квадрат, куб, в к –ую степень, получить Ак
4) А0 =Е
Пример 2. Предприятие выпускает продукцию трех видов Р1, Р2, Р3 и использует сырье двух типов S1 и S2.
Матрица А3х2 (технологическая). Показывает, сколько единиц сырья j-го типа расходуется на производство продукции i-го вида.
А= 
План выпуска продукции задан вектором- строкой С,
С= 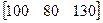
Стоимость единицы сырья каждого типа задается вектором – столбцом В
В= 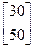
Матрица – строка затрат сырья может быть записана в матричном виде S = CA = 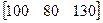
 =
= 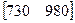
Тогда общая стоимость сырья
Q = SB = 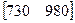
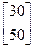 =730*30 + 980*50 = 70900 ден. ед.
=730*30 + 980*50 = 70900 ден. ед.
3. Применение матриц в задаче планирования производства
Предприятие выпускает n видов продукции, используя для этого m видов ресурсов. Известна технологическая матрица Аmxn затрат ресурсов на производство единицы каждого вида продукции. Элемент ai,j равен количеству ресурса i-го вида (i = 1..m), необходимого для производства продукта j-го вида (j=1..n). Каждый столбец матрицы А описывает некую технологию.
Известен вектор b (bi, i=1..m), имеющихся в распоряжении предприятия объемов ресурсов.
Известен также вектор C удельной прибыли предприятия. Элемент сj, j=1..n, - прибыль предприятия от реализации единицы продукции j–го вида.
Если обозначить через xj план производства продукции j–го вида, то производственная программа будет задаваться вектором Х
Тогда произведение АХ характеризует суммарные расходы ресурсов на реализацию плана. Очевидно, АХ ≤ b, т.е.
ai,1x1 + ai,2x2+…+ai,nxn ≤ bi i=1..m
Прибыль предприятия от реализации всей произведенной продукции равна
z= с1x1+ c2x2 +…+cnxn
Задача заключается в том, чтобы отыскать такой план производства, который обеспечит предприятию наибольшую прибыль
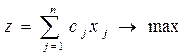
Поставленная выше задача является оптимизационной, решается методом линейного программирования. Метод был разработан лауреатом Нобелевской премии в области экономики, академиком Л. В. Конторовичем.
|
|
|

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!