· Вероятность того, что случайная величина x примет значение  :
:
 ,
,
где N – полное число измерений, N i – число опытов, в которых величина x принимает значение  .
.
· Условие нормировки. Сумма вероятностей по всем возможностям есть достоверное событие, вероятность которого равна единице:
 .
.
· Среднее арифметическое значение случайной величины x:
 , или
, или  ,
,
где  – значение величины x в i -том измерении; N – число измерений;
– значение величины x в i -том измерении; N – число измерений;  – вероятность того, что величина x принимает значение
– вероятность того, что величина x принимает значение  .
.
· Среднее квадратичное случайной величины x:
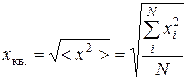 .
.
· Вероятность dw того, что случайная величина принимает значения в интервале от x до x+dx ( ), прямо пропорциональна величине интервала dx:
), прямо пропорциональна величине интервала dx:
 ,
,
где коэффициент пропорциональности f (x), зависящий от x, это – функция распределения вероятностей случайной величины x.
· Условие нормировки функции распределения вероятностей:
 , или
, или  .
.
· Вероятность dw того, что молекула идеального газа имеет скорость в промежутке от 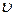 до
до  (
( ), равна отношению числа
), равна отношению числа 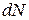 молекул, обладающих скоростями в заданном промежутке, к полному числу молекул N:
молекул, обладающих скоростями в заданном промежутке, к полному числу молекул N:
 .
.
· Число 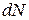 молекул идеального газа, имеющих скорости в промежутке от
молекул идеального газа, имеющих скорости в промежутке от 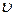 до
до  (
( ), пропорционально полному числу молекул N и величине интервала скоростей
), пропорционально полному числу молекул N и величине интервала скоростей  :
:
 ,
,
где 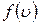 – функция распределения Максвелла (см. рис.6.1), равная
– функция распределения Максвелла (см. рис.6.1), равная
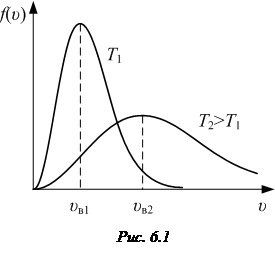
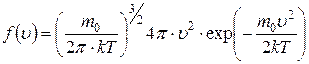 .
.
Здесь 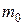 – масса одной молекулы;
– масса одной молекулы;  – постоянная Больцмана; T – абсолютная температура. Если интервал скоростей мал:
– постоянная Больцмана; T – абсолютная температура. Если интервал скоростей мал:  , то число
, то число 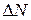 молекул со скоростями
молекул со скоростями  равно
равно
 ;
;
иначе
 .
.
· Доля молекул идеального газа, имеющих скорости в промежутке от 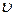 до
до  (
( ), равна
), равна  .
.
· Характерные скорости молекул газа:
- средняя арифметическая:  , или
, или
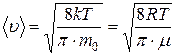 ;
;
- средняя квадратичная: 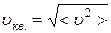 , где
, где 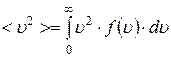 , или
, или
 ;
;
- наиболее вероятная (соответствует максимуму функции распределения Максвелла, см. рис. 6.1):
 .
.
Здесь 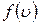 – функция распределения Максвелла по скоростям;
– функция распределения Максвелла по скоростям; 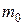 – масса одной молекулы;
– масса одной молекулы;  – молярная масса газа;
– молярная масса газа;  – постоянная Больцмана; T – абсолютная температура;
– постоянная Больцмана; T – абсолютная температура;  – универсальная газовая постоянная.
– универсальная газовая постоянная.
· Распределение Больцмана – это равновесное распределение частиц в потенциальном поле:
 , или
, или 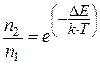 .
.
Здесь  – концентрации частиц в произвольной точке силового поля;
– концентрации частиц в произвольной точке силового поля;  – их потенциальная энергия в данной точке;
– их потенциальная энергия в данной точке;  – концентрации частиц в точке, где потенциальная энергия равна нулю;
– концентрации частиц в точке, где потенциальная энергия равна нулю;  – постоянная Больцмана; T – абсолютная температура; n 1 и n 2 – концентрации частиц в двух точках потенциального поля; Δ E = E 2– E 1 – разность их потенциальных энергий в этих точках.
– постоянная Больцмана; T – абсолютная температура; n 1 и n 2 – концентрации частиц в двух точках потенциального поля; Δ E = E 2– E 1 – разность их потенциальных энергий в этих точках.
· Барометрическая формула – закон уменьшения давления p идеального газа с высотой h в однородном потенциальном поле при постоянной температуре:
 .
.
Здесь μ – молярная масса газа, p 0 –давление при h =0, T – абсолютная температура, m 0 – масса молекулы, R – универсальная газовая постоянная.
Явления переноса
· Среднее число столкновений молекулы с другими молекулами в единицу времени:
 ,
,  ,
,
где 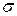 – эффективное сечение молекулы; n – концентрация молекул;
– эффективное сечение молекулы; n – концентрация молекул; 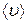 – средняя арифметическая скорость молекул;
– средняя арифметическая скорость молекул;  – средняя длина свободного пробега.
– средняя длина свободного пробега.
· Среднее время свободного пробега (средняя продолжительность свободного пробега):
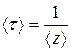 ,
,  .
.
· Эффективное сечение молекулы
 ,
,
где d – эффективный диаметр молекулы.
· Средняя длина свободного пробега
 ,
,  ,
,
где n – концентрация молекул; 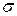 – эффективное сечение молекулы; d – эффективный диаметр молекулы.
– эффективное сечение молекулы; d – эффективный диаметр молекулы.
· Уравнение диффузии (закон Фика). Число частиц 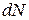 , перенесённых за время
, перенесённых за время 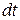 через малую площадку
через малую площадку  , пропорционально градиенту концентрации
, пропорционально градиенту концентрации  вдоль оси OZ, перпендикулярной площадке:
вдоль оси OZ, перпендикулярной площадке:
 , или
, или  .
.
Здесь D – коэффициент диффузии, равный
 .
.
· Масса вещества, перенесённого за время 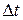 через площадку
через площадку  :
:
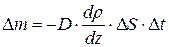 ,
,
где  – градиент плотности, D – коэффициент диффузии.
– градиент плотности, D – коэффициент диффузии.
· Закон Ньютона для вязкости. Сила вязкого трения, возникающая между слоями газа, движущимися параллельно, но с разными скоростями, пропорциональна градиенту  скорости направленного движения слоёв в направлении, перпендикулярном скорости (рис. 6.2):
скорости направленного движения слоёв в направлении, перпендикулярном скорости (рис. 6.2):

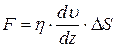 ,
,
где  – площадь слоёв;
– площадь слоёв;  – динамическая вязкость.
– динамическая вязкость.
· Импульс, перенесённый за время 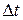 через площадку
через площадку  в результате действия сил вязкости:
в результате действия сил вязкости:
 ,
,
где  – градиент скорости,
– градиент скорости,  – коэффициент динамической вязкости.
– коэффициент динамической вязкости.
· Коэффициент динамической вязкости (вязкость):
 ,
, 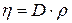 ,
,
где  – плотность газа;
– плотность газа; 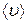 – средняя арифметическая скорость молекул;
– средняя арифметическая скорость молекул;  – средняя длина свободного пробега; D – коэффициент диффузии.
– средняя длина свободного пробега; D – коэффициент диффузии.
· Закон Фурье. Количество теплоты, перенесённой через малую площадку  за время
за время 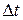 в результате теплопроводности, пропорционально градиенту температуры
в результате теплопроводности, пропорционально градиенту температуры  :
:
 ,
,
где  – коэффициент теплопроводности, равный
– коэффициент теплопроводности, равный
 , или
, или  , или
, или  .
.
Здесь  – плотность газа;
– плотность газа; 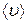 – средняя арифметическая скорость молекул;
– средняя арифметическая скорость молекул;  – средняя длина свободного пробега; D – коэффициент диффузии;
– средняя длина свободного пробега; D – коэффициент диффузии;  – коэффициент динамической вязкости;
– коэффициент динамической вязкости; 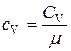 и
и  – удельная и молярная теплоемкости идеального газа при постоянном объёме; i – число степеней свободы;
– удельная и молярная теплоемкости идеального газа при постоянном объёме; i – число степеней свободы;  – молярная масса газа, R – универсальная газовая постоянная.
– молярная масса газа, R – универсальная газовая постоянная.



 :
: ,
, .
. , или
, или  ,
, – вероятность того, что величина x принимает значение
– вероятность того, что величина x принимает значение 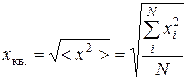 .
. ), прямо пропорциональна величине интервала dx:
), прямо пропорциональна величине интервала dx: ,
, , или
, или  .
.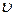 до
до  (
( ), равна отношению числа
), равна отношению числа 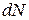 молекул, обладающих скоростями в заданном промежутке, к полному числу молекул N:
молекул, обладающих скоростями в заданном промежутке, к полному числу молекул N: .
. :
: ,
,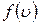 – функция распределения Максвелла (см. рис.6.1), равная
– функция распределения Максвелла (см. рис.6.1), равная
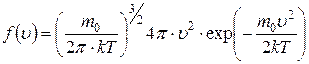 .
.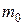 – масса одной молекулы;
– масса одной молекулы;  – постоянная Больцмана; T – абсолютная температура. Если интервал скоростей мал:
– постоянная Больцмана; T – абсолютная температура. Если интервал скоростей мал:  , то число
, то число 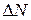 молекул со скоростями
молекул со скоростями  равно
равно ;
; .
. .
. , или
, или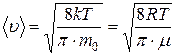 ;
;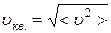 , где
, где 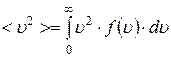 , или
, или ;
; .
. – молярная масса газа;
– молярная масса газа;  – универсальная газовая постоянная.
– универсальная газовая постоянная.  , или
, или 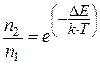 .
. – концентрации частиц в произвольной точке силового поля;
– концентрации частиц в произвольной точке силового поля;  – их потенциальная энергия в данной точке;
– их потенциальная энергия в данной точке;  – концентрации частиц в точке, где потенциальная энергия равна нулю;
– концентрации частиц в точке, где потенциальная энергия равна нулю;  .
. ,
,  ,
,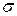 – эффективное сечение молекулы; n – концентрация молекул;
– эффективное сечение молекулы; n – концентрация молекул; 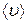 – средняя арифметическая скорость молекул;
– средняя арифметическая скорость молекул;  – средняя длина свободного пробега.
– средняя длина свободного пробега.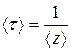 ,
,  .
. ,
,  ,
,  ,
,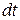 через малую площадку
через малую площадку  , пропорционально градиенту концентрации
, пропорционально градиенту концентрации  вдоль оси OZ, перпендикулярной площадке:
вдоль оси OZ, перпендикулярной площадке: , или
, или  .
. .
.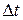 через площадку
через площадку 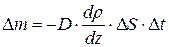 ,
, – градиент плотности, D – коэффициент диффузии.
– градиент плотности, D – коэффициент диффузии. скорости направленного движения слоёв в направлении, перпендикулярном скорости (рис. 6.2):
скорости направленного движения слоёв в направлении, перпендикулярном скорости (рис. 6.2):
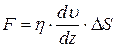 ,
, – динамическая вязкость.
– динамическая вязкость. ,
, ,
, 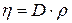 ,
, – плотность газа;
– плотность газа;  :
: ,
, – коэффициент теплопроводности, равный
– коэффициент теплопроводности, равный , или
, или  , или
, или  .
.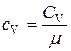 и
и  – удельная и молярная теплоемкости идеального газа при постоянном объёме; i – число степеней свободы;
– удельная и молярная теплоемкости идеального газа при постоянном объёме; i – число степеней свободы; 


