

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Интересное:
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Основы демографической статистики и моделирование.
Рассмотрим модель динамики населения с учётом возрастной структуры:
Пусть
l(t,x)-количество моделей в возрасте x в момент времени t
l(0,x)-распределение людей по возрасту в некоторый начальный момент времени – кол-во людей в «нуле»
l(t,0)-скорость рождения – сколько людей рождается в момент времени t
 , или
, или 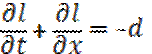
где μ(x) -интенсивность смертей (смертность) - какая-то часть людей возраста x, умерших в момент вр. t,
 d=μ*l -абсолютная смертность (количество умерших)
d=μ*l -абсолютная смертность (количество умерших)

 ,
,
Где [  ]-фертильный возраст – интервал фертильности,
]-фертильный возраст – интервал фертильности,

 -функция рождаемости.
-функция рождаемости.
[  +/- ∆] - м одель с включением миграции
+/- ∆] - м одель с включением миграции
Точно такой же моделью описывается движение рек (коэф. v - скорость реки):  )
)
x- расстояние, l-количество загрязняющих веществ, 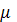 -самовосстановление реки.
-самовосстановление реки.
Пусть популяция стационарна, не зависит от t, то есть смертность и рождаемость постоянны во времени. В этом случае частные производные превращаются в ноль, кроме производной по возрасту:
 - стационарное возрастное распределение
- стационарное возрастное распределение
 -количество родившихся (
-количество родившихся ( )
)
Подставив, получим  – демографический потенциал.
– демографический потенциал.
Если соблюдать равенство, то распределение стационарно,  сокращается, и сравниваем:
сокращается, и сравниваем:
если  , то популяция не будет стационарной,
, то популяция не будет стационарной,
если же  , то популяция стационарна.
, то популяция стационарна.
Если бы интенсивность смерти и рождаемости не зависели от t, то получаем зависимость от возраста (выше – lx=… - стац.возраст.распред.) - такая модель лежит в основе актуарных расчётов, но рассматривается не всё население, а когорта. Рассм, как меняется во времени их численность:
 - некоторое количество людей, которые родились в один год
- некоторое количество людей, которые родились в один год
 -умершие до года (детская смертность) – 10% - вызывает скачок l(x)
-умершие до года (детская смертность) – 10% - вызывает скачок l(x)
|
|

 -момент рождения
-момент рождения  человек – начало координат
человек – начало координат

 -постепенно умирают
-постепенно умирают
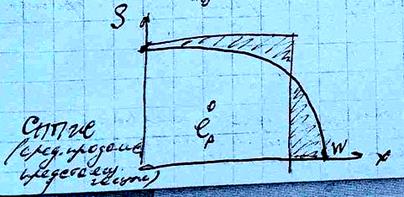
-к годам x=100 – обозначается w - никого не остаётся
 100 x
100 x
Кривая  называется кривой дожития, означает, какая часть людей доживает до возраста x. Чтобы построить функцию, необходимо иметь статистику по когорте. Функция строится в табличном виде, данные статистики вносятся в таблицу выживания (или таблицу смертности).
называется кривой дожития, означает, какая часть людей доживает до возраста x. Чтобы построить функцию, необходимо иметь статистику по когорте. Функция строится в табличном виде, данные статистики вносятся в таблицу выживания (или таблицу смертности).
 |: lо Þ
|: lо Þ  , это получим, решая дифференциальное уравнение
, это получим, решая дифференциальное уравнение
В результате  , s(x) –это доля живущих, выживших (сл-но, вероятность).
, s(x) –это доля живущих, выживших (сл-но, вероятность).
Теоретические законы смертности – нбх знать вид функции интенсивности смерти, чтобы определить вероятностные хар-ристики стац.возраст.распределения.
1) 
 По аналогии с популяциями животных
По аналогии с популяциями животных

 , тогда
, тогда 


 |
2) Закон де Муавра (1729)

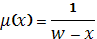 , где w-некоторый предельный возраст
, где w-некоторый предельный возраст

3) З-н Гомперца (1825)
 , a, B-некоторые коэффициенты, раскроем s: =>
, a, B-некоторые коэффициенты, раскроем s: => 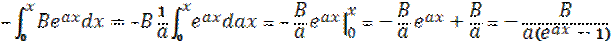
s(x)=exp{  }
}
Зависимость объясняет, что поскольку d=  m должна иметь максимум, этот максимум смертей попадает на определённый возраст жизни. В этом возрасте вероятность смерти выше по сравнению с остальными.
m должна иметь максимум, этот максимум смертей попадает на определённый возраст жизни. В этом возрасте вероятность смерти выше по сравнению с остальными.
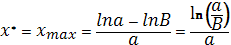 , где максимум берется по функции f=ms=-ds/dx
, где максимум берется по функции f=ms=-ds/dx
(это были основные, дополнительные дальше)
4) Модель Мэйкхема
 - добавляется к предыдущей модели коэф. A-учитывает некоторый фон, связанный с эпидемиями, бедствиями, различными катастрофами
- добавляется к предыдущей модели коэф. A-учитывает некоторый фон, связанный с эпидемиями, бедствиями, различными катастрофами
5)Закон Вейбула
 ,
,
s(x)=exp{  }
}
6) Распределение Перкса

 -является вогнутой и хуже описывает ситуацию (остальные были вогнутые)
-является вогнутой и хуже описывает ситуацию (остальные были вогнутые)
(функция s(x) довольно громоздкая)
Вероятностная интерпретация стационарного распределения






 Введём случайную величину X – продолжительность жизни при рождаемости. Тогда P(X>x)=s(x), F(x)=P(X≤x)=1-s(x)
Введём случайную величину X – продолжительность жизни при рождаемости. Тогда P(X>x)=s(x), F(x)=P(X≤x)=1-s(x)
s(x)
P( >x)
>x)
x
Найдём вероятность умереть на интервале
Пусть t малая величина, тогда:
t 
-мгновенная смерть/интенсивность смертей
S=1-F
S`=-fÞm(x)=  – показывает риск умереть в возрасте х – функция риска.
– показывает риск умереть в возрасте х – функция риска.
Основные вероятностные характеристики, используемые в страховании жизни (безусловные и условные вероятности дожития, интенсивность смертности, средняя продолжительность жизни при рождении, средняя остаточная продолжительность жизни). Таблицы выживаемости (смертности). Отличие средних при использовании непрерывной и дискретной моделей.
|
|






 Введём случайную величину X – продолжительность жизни при рождаемости. Тогда P(X>x)=s(x), F(x)=P(X≤x)=1-s(x)
Введём случайную величину X – продолжительность жизни при рождаемости. Тогда P(X>x)=s(x), F(x)=P(X≤x)=1-s(x)
s(x)
P( >x)
>x)
x
Введём случайную величину L(x) – количество людей доживших до возраста x, причём lx – конкретная фактическая известная величина, поэтому значение приближённое:
l(x)=EL(x) ~~  , т.е. l(x)=
, т.е. l(x)=
I-индикатор события дожития A=( >x) (дожил-1, не дожил-0), поэтому её мат.ож. равно вер-ти А.
>x) (дожил-1, не дожил-0), поэтому её мат.ож. равно вер-ти А.
Обознач.  -если величина дискретная, l(x) - если возраст считать непрерывной величиной
-если величина дискретная, l(x) - если возраст считать непрерывной величиной
На практике используется не функция, а таблица (дискретная вел-на кол-ва людей):
| x | 
| 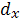
| 
| 
|

| ||||

| ||||
| … | ||||

|
Начальная графа – стартовый размер когорты  -корень таблицы, который показывает её точность (1000, 10000, …), и чем больше, тем точнее.
-корень таблицы, который показывает её точность (1000, 10000, …), и чем больше, тем точнее.
Количество умерших за год в когорте: dx= 
Вероятность того что человек дожил до возраста x, но вероятность мереть в следующем году: 
Это вероятность условная - при условии, что человек дожил
Вероятность прожить ещё год: 
Количество смертей (умерших), человек дожил до возраста x, но умер в ближайшие n лет: ndx= 
Соответственно условные вероятности
n  =ndx/
=ndx/  ; n
; n 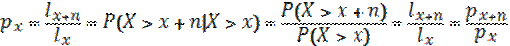
Найдём вероятность умереть на интервале [x, x+t]:
P(x<X≤x+t|X>x)= 

Пусть t малая величина, тогда:
t 
-мгновенная смерть/интенсивность смертей
S=1-F
S`=-fÞm(x)=  – показывает риск умереть в возрасте х
– показывает риск умереть в возрасте х
В теории вероятности такая функция называется функцией риска
Среднее время жизни.
1) Среднее время жизни при рождении. 

2) Остаточная продолжит.жизни – случ.величина, её мат.ож – средняя остаточная продолжит.жизни

Найдем распределение  :
:



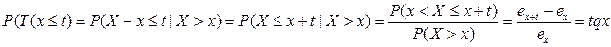
вероятность умереть в интервале(x;x+t)

T(x)=X-x (?)

t – сколько осталось прожить


 - приближенно
- приближенно


Рассмотрим вероятность того, что человек, доживший до возрастра x проживет еще m лет, но умрет в последующий n лет:



- отложенная смерность
|
|
|

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!