Управляющий граф содержит цикл, порожденный операторами while или repeat

Циклы while и repeat анализировать сложнее, чем оператор for, так как количество исполнений тела цикла зависит от истинности или ложности условия и, может быть, достаточно сложных изменений в теле цикла значений переменных, входящих в состав условия.

Рассмотрим в качестве примера вычисление 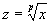методом Ньютона (имеется в виду вычисление вещественного значения корня). Задача сводится к нахождению корня уравнения x^(1/p) - z = 0, который, в свою очередь, отыскивается с помощью итерационного процесса

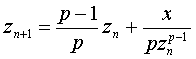
начинающегося некоторым начальным значением z₀, выбираемым возможно наиболее близким к корню. Окончание процесса происходит, когда корень оказывается найденным с заданной точностью ε с помощью, например, следующей функции.

function P_root(p: integer; x, z0, epsilon: real): real; var i: integer; old, z: real; begin z:= z0; repeat old:= z; у:= old; for i:= 2 to p - 1 do у:= y*old; z:= (p - l)*old/p + x/ (p*y); until abs(z - old) < epsilon; end;

Из теории численных методов известно, что требуемое количество n итераций для достижения заданной точности имеет порядок 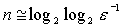. Этот процесс сходится (заканчивается) очень быстро: уже при 5 итерациях достигается точность выше 10^-9.

В общем случае условие в операторе while или в операторе repeat делит область комбинаций исходных и промежуточных данных, т.е. область возможных состояний программы на момент начала исполнения оператора цикла на две части: для первой условие выполняется, а для второй - нет. Если начальное состояние принадлежит первой подобласти (для while) или второй подобласти (для repeat), то с каждым выполнением тела цикла состояние (как точка в пространстве состояний) будет перемещаться по некоторой траектории, зависящей от операций, заданных в теле, до тех пор, пока не пересечет границу области. Именно количество шагов до пересечения границы и определяет сложность этого участка программы.

На следующем шаге мы рассмотрим анализ сложности рекурсивных алгоритмов.

На этом шаге мы рассмотрим анализ сложности рекурсивных алгоритмов.

Рассмотрим сначала случай прямой рекурсии с единственным (вне какого-либо цикла) рекурсивным вызовом в теле процедуры. Примером такого алгоритма является алгоритм Евклида вычисления наибольшего общего делителя.

Напомним, что текст рекурсивной процедуры с вектором исходных данных X содержит вызов этой же процедуры с измененным по некоторому правилу вектором исходных данных Y = f(X). Кроме этого, в тексте содержится некоторое нерекурсивное вычисление h(X) и операции сравнения c(Х,S) значения X со значением S, при котором рекурсивный процесс должен заканчиваться. Обозначим "точное" (а не верхнюю границу или среднее) значение сложности при входных данных X через Тα(X). Тогда

Тα(X) = Тα(Y) + Th(X) + Tc(X,S),

или

Тα(X) = Тα(АХ)) + Tf(X) + Th(X) + Tc(X,S).

Второе соотношение представляет собой рекуррентное уравнение для определения значений неизвестной функции Тα(X) через известные значения f(A), Tf(X), Th(X), Tc(X,S). Кроме этого, имеется начальное условие Tα(S)=Ts(S) с известной функцией сложности вычисления (нерекурсивного) значения S. Таким образом, имеется система:

Тα(Х) =Tα(f(X))+ Tf(X)+Th(X)+ Тc(X, S)

Tα(S)=Tc(S,S)+Ts(S)

Это частный случай рекуррентного уравнения. Такие уравнения имеют развитую теорию. В некоторых случаях возможно аналитическое решение. Покажем его применение на примере рекурсивного вычисления факториала:

function FACTORIAL (х: integer): integer;

Begin

if x = 1 then FACTORIAL:= 1

else FACTORIAL:= x * FACTORIAL (x-1);

end;

Здесь X = x, S = 1, f(X)=X-1, Tf(X)=1, Th(X) = 2, Tc(X,S)=l, Ts(S) = 1. Таким образом, система уравнений превращается в

Тα(x) = Тα(х-1)+4, Тα(1) = 2.

Ее решение - Тα(x) = 4х-2.

Верхняя оценка Тα(V) может быть получена подобным образом, но с использованием рекуррентных неравенств:

Тα(V) <= Тα(f(V))+Tf(V)+Th(V)+Tc(V,V0),

Tα(V0) <= Tc(V0, Vo)+Ts(V0).

Оценка среднего значения сложности требует учета вероятностных законов и может быть значительно более трудной. Вообще говоря, нельзя использовать написанные выше рекуррентные уравнения в вероятностном случае: среднее значение функции случайной величины не равно значению функции от среднего значения случайной величины,

среднее (f(X)) <> f(среднее (X)),

кроме случая линейной функции f.

Теперь рассмотрим более общий случай прямой рекурсии с несколькими рекурсивными вызовами в теле процедуры. Эти вызовы могут иметь разные аргументы Y1, Y2,...,Yk, где Y1 =f_l(X), Y2 =f₂(X),..., Yk=f_k(X). Рекуррентное уравнение для функции сложности имеет вид

Тα(X) = Тα(f₁(X)) + Тα(f₂(X)) +... + Тα(f_k(X)) + Tf₁(X) + Тf₂(X) +...+

Тf_k(X) + Тh (X) + Tc (X, S)

Тα(S) = Tc (S, S) + Ts (S).

В реальных рекурсивных алгоритмах встречаются различные функции f_i(X), однако, подчиняющиеся обычно определенным закономерностям. Эти наиболее часто встречающиеся случаи мы сейчас рассмотрим.

1. Одинаковые функции f_l(X) =...= f_k(X) = f(X). Рекуррентное уравнение для функции сложности имеет вид:

Тα(X) = k Тα (f(Х))+kTf(X)+Th(X) + ТС(Х, S),

Tα(S)=Tc(S,S)+Ts(S).

Решение этого уравнения зависит от соотношения k и f(X). Ясно, что если k > 1, то значения Tα (X) быстро возрастают с ростом X (если значения могут быть упорядочены) или Tα (V) быстро возрастают с ростом V, если функция f недостаточно быстро уменьшает X. Первый пример как раз такого рода: k = 2, f(X)=Х-1.

Проведем анализ решения известной головоломки "Ханойская башня" (рисунок 1) - игры, основанной на древнем ритуале брахманской башни, с помощью которого, по преданию, брахманские жрецы предсказывали конец света.

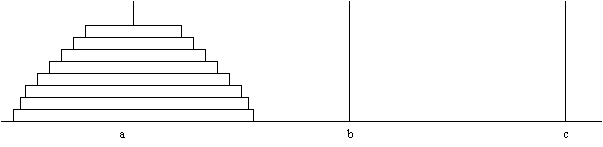
Рис.1. Ханойская башня

Задача состоит в следующем.

Имеется три алмазных иглы: a, b, c. В момент творения на иглу а нанизываются 64 золотых диска уменьшающихся размеров (будем рассматривать задачу для n дисков). Все диски имеют разный диаметр, внизу находится самый большой диск, а наверху - самый маленький. Никакой диск большего диаметра не может находиться выше диска меньшего диаметра. На иглах b и с дисков нет. Перед брахманскими жрецами, только что посвященными в сан, ставится задача переложить диски на иглу b. При этом иглой с можно пользоваться как временной емкостью. Конец света наступит, когда все 64 диска окажутся на игле b в том же порядке, в котором они располагались на игле a.

С алгоритмической точки зрения элементарным шагом является перенос одного диска. В задаче имеется важное ограничение: ни на одной из игл никогда не должно возникать ситуации, при которой диск большего диаметра лежит на диске меньшего диаметра.

Рекурсивное решение этой задачи выглядит естественно и просто. Пусть процедура CARRY (n, а, b, c) переносит башню высоты n с иглы а на иглу b, используя иглу c как вспомогательную. Тогда исходная задача может быть разбита на три части:

CARRY (n-1, а, с, b) {Перенести верхние n-1 дисков на с.}

CARRY (1, а, b, -); {Перенести один (нижний) диск на b.}

CARRY (n-1, с, b, а); {Перенести башню с c на большой диск, уже находящийся на b.}

Вторая часть тривиальная, одношаговая. Выделим ее в отдельную нерекурсивную процедуру ONEDISK (a,b). Теперь можно написать рекурсивную процедуру:

procedure CARRY (n, а, b, c: integer);

Begin

if n > 1 then

Begin

CARRY (n-1, а, с, b);

ONEDISK (a,b);

CARRY (n-1, c, b, a)

end;

end;

Сложность процедуры ONEDISK - константа (обозначим ее K). Входной набор Z = (n, а, b, с). Достаточно очевидно, что номера игл а, b, с никак не влияют на сложность. Поэтому можно принять V = n. Рекурсивное уравнение примет вид:

Тα (n) = 2Тα (n-1) +2 + h + 1,

Тα (1) = 1 + 0, или

Тα (n) = 2Тa (n-1) + h + 3, Тα (1) = 1.

Решение этого уравнения может быть получено в виде:

Тα (n) = v 2n + w,

где v, w - параметры, подлежащие определению.

Уравнения для определения v и w получаются из предыдущих рекуррентных соотношений:

v2n + w = 2v2(n-1) + 2w + h + 3, v2 + w = 1

Итого,

Tα (n) = (2 + h/2) 2n - (h + 3).

Найденная оценка сложности относится к классу так называемых экспоненциальных функций временной сложности.

Второй тип рекуррентных уравнений, часто встречающихся в анализе алгоритмов, может быть задан следующими формулами:

Tα (V) = k Tα (V/m) +lV,

Тα (1) = l,

при этом предполагается, что сложность данных V - натуральное число.

При отсутствии явного выражения решения в виде формулы, включающей элементарные функции, обычно удовлетворяются асимптотическим решением, т. е. приближенной формулой, точность которой возрастает с ростом V.

Асимптотическое решение уравнений этого типа будет следующим:

Тα (V) = О (V), если k < m,

Тα (V) = О (V logV), если k = m,

Тα (V) = О (V ^log_m^k), если k > m.

2. Функции, образующие прогрессию Х-1, Х-2,..., Х-k.

Пример такой процедуры для k-2 уже был приведен - рекурсивная процедура для нахождения n -го числа Фибоначчи. Проведем более детальный ее анализ.

function Fr (n: integer): integer;

Begin

if n = 1 or n = 2 then Fr:= 1

else Fr:= Fr(n-1) + Fr(n-2);

end;

Здесь сразу можно взять Х= n, Tf₁(n) = Tf₂(n) = 1, Th (n) = 2, Тс(n) = 2, Ts (n) = 1. Уравнения для функции сложности: Тα (n) = Тα (n-1) + Тα (n-2) + 6, Тα (2) = 3, Тα (1) = 3.

На следующем шаге мы рассмотрим случай косвенной рекурсии.

На этом шаге мы рассмотрим случай косвенной рекурсии.

Если две процедуры A и B связаны косвенной (взаимной) рекурсией, то для каждой из них можно записать выражения функции сложности и объединить их в общую систему уравнений. Поскольку одна из процедур, например, B имеет нерекурсивную ветвь, то эта ветвь порождает начальные условия. В простом случае однократного вызова процедуры B в теле A (и процедуры A в теле B) уравнения имеют вид:

T_A(X) = Т_B(f_A(X)) + T_fA(Х)+ Т_hA(X),

Т_B(X) = Т_A(f_B(X)) + Т_fB(Х)+ Т_hB(X) + Т_cВ(X, S),

T_B(S) = T_cB(S,S) + T_sB(S)

Первые два уравнения с двумя неизвестными функциями могут быть подстановкой во второе уравнение вместо T_A правой части первого уравнения (с соответствующим изменением аргумента) сведены к одному уравнению для определения T_B. Третье уравнение останется в качестве начального условия. Таким образом, задача определения функции сложности в случае косвенной рекурсии будет сведена к той же задаче для прямой рекурсии.

На следующем шаге мы рассмотрим особые случаи анализа сложности рекурсивных алгоритмов.

На этом шаге мы рассмотрим осбые случаи анализа сложности рекурсивных алгоритмов.

Если функция f(Х) преобразования аргумента при рекурсивном вызове нелинейна, то аналитическое отыскание функции сложности алгоритма редко бывает возможно. Общих методов в этом случае нет, и приходится привлекать сведения из соответствующей проблемной области, а не только информацию о структуре программы. Аналогичная ситуация имеет место и для итеративных алгоритмов при оценке числа выполнений тела цикла while или repeat. Интересным примером такого рода является алгоритм Евклида отыскания наибольшего общего делителя. Напомним его текст.

function GCD (n, m: integer): integer;

Begin

if m = 0 then GCD:= n

else GCD:= GCD (m, n mod m);

end;

Здесь функция f(X) = f(n,m) = (m,n mod m) переставляет второй аргумент на место первого, а на место второго аргумента ставит значение f(n,m). Это нелинейное преобразование.

Оценим сверху количество рекурсивных вызовов функции GCD. Для этого выпишем последовательно соотношения, определяющие аргумент X. Предположим для определенности, что n > m (при обратном неравенстве первый вызов функции просто меняет аргументы местами, а при равенстве n = m процесс завершается за один шаг). В качестве параметра V сложности исходных данных целесообразно принять меньший из аргументов функции, т.е. V = m, так как именно с него начинаются операции деления (нахождения модулей) - если увеличить m на произвольно большое число, кратное m (например, m*10¹⁰⁰⁰), то это не изменит количества шагов. Следовательно, max(n,m) не является хорошим аргументом функции сложности.

При рекурсивных вызовах вычисляются остатки от деления, которые мы обозначим R_i: R_i=R_(i-2) mod R_(i-1). Начало процесса определяется значениями R₀ = n, R₁ = m. Иначе остатки можно определить системой равенств:

R₀ = R₁d₁ + R₂,

R₁ = R₂d₂ + R₃,

R₂ = R₃d₃ + R₄,

.....

R_k-2 = R_k-1d_k-1 + R_k,

R_k-1 = R_kd_k

где d_i - частные от деления. Процесс завершается, когда очередной остаток от деления будет равен нулю. Очевидно, что процесс будет наиболее длительным, если все d_i = 1. Перенумеруем последовательность остатков с конца:

R_k+1 = 0 = F₀,

R_k = F₁,

R_k-1 = F₂,

.....

R_k-i+1 = F_i,

R₁ = F_k.

Тогда предыдущую систему при условии d_i = 1 можно записать в виде одного рекуррентного уравнения

F_i = F_(i-1) + F_(i-2)

при начальных условиях F₀ = 0, F₁ = F₂ и условии на конце: F_k равно m или ближайшему к m снизу числу, удовлетворяющему рекуррентному уравнению. Заметим, что не требуем, чтобы F_(k+l) = m, так как это требование может (но не всегда) войти в противоречие с условиями d_i=1. Последовательность F_i пока еще не определена однозначно - не хватает начального условия - значения F₁. Это значение мы выберем так, чтобы последовательность имела максимальную длину (при условии F_k = m). Очевидно, это должно быть минимальное ненулевое значение, т. е. F₁ = 1.

Становится ясно, что последовательность {F_i} - это последовательность чисел Фибоначчи. Теперь задача получения верхней оценки сложности алгоритма Евклида сводится к следующему: найти номер k максимального из чисел Фибоначчи F_k <= m.

Величина k и является оценкой сложности алгоритма.

Из теории чисел Фибоначчи известно, что F_k может быть выражено формулой

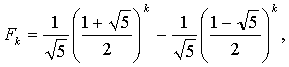
число

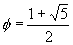
известно как золотое сечение, φ= 1,618. Поскольку второе слагаемое в формуле для F_k не превышает по абсолютной величине единицы, то можно написать следующие неравенства:

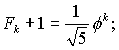
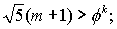
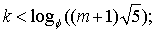
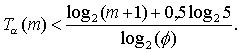
Вывод средней оценки сложности алгоритма Евклида приведен в книге Д. Кнута (Т. 2, разд. 4.5.3). Однако, когда оценка худшего случая всего лишь логарифмическая, средняя оценка представляет, в основном, теоретический интерес (в данном случае она тоже логарифмическая, но с меньшим коэффициентом).

С точки зрения анализа, как худшего, так и среднего, случаев интересна теорема Э.Чезаро: пусть q_N - число упорядоченных пар целых чисел (n, m), таких, что 1 <= n, m <= N и НОД (n,m) = 1. Тогда:

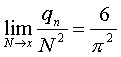
Она говорит о том, что в 60% случаев алгоритм Евклида будет заканчиваться получением остатка, равного 1; такой остаток мы рассматривали как худший случай при анализе сложности.

Замечание о золотом сечении. Определенное выше число φ, называемое золотым сечением и приблизительно равное 34/21, имеет довольно богатую историю. Помимо того, что оно возникает при решении чисто математических задач, им интересуются искусствоведы и психологи. В книге "Введение в эстетику" немецкий ученый Г. Т. Фехнер приводит следующие данные. Для изучения предпочтений по отношению к форме было взято десять прямоугольных карточек из белого картона, равных по площади квадрату со стороной 8 см, но с различными соотношениями сторон. Наименьшее отношение сторон соответствует квадратной карточке и равно 1:1, наибольшее - 5:2. Между этими крайними значениями имеется золотое сечение с отношением сторон 34:21. Различным людям ставился вопрос: какие из прямоугольников при максимальном абстрагировании от их возможного применения являются наиболее, а какие - наименее привлекательными? Более трети предпочли "золотое сечение", три близких отношения 34:21, 3:2, 23:13 предпочли в сумме около 73% опрошенных, никто не назвал золотое сечение наименее привлекательным. Более подробно об этом можно прочесть в книге "Семиотика и искусствометрия" (М: Мир, 1972).

На следующем шаге мы рассмотрим сложность операций с бинарными деревьями.

На этом шаге мы рассмотрим сложность операций с бинарными деревьями.

Бинарные деревья часто используются для хранения информации. Они выгодно отличаются от массивов фиксированного размера своим динамическим характером, возможностью почти неограниченно увеличивать объемы хранимой информации. От линейных списков их отличают лучшие временные характеристики - например, при поиске элемента (наиболее часто используемой операции) требуется в среднем просмотреть меньшую часть дерева, чем это требовалось бы для списка с таким же количеством элементов. Проведем детальный анализ функций сложности этих операций.

Прежде всего определим, какой параметр можно рассматривать в качестве параметра V сложности данных. Наиболее очевидным кандидатом на эту роль является текущее количество n вершин в дереве. Но ясно, что величина n не определяет однозначно сложность. Есть хорошие и плохие деревья. Оценим с этой точки зрения параметр n - насколько при одном и том же значении n для разных деревьев могут отличаться функции сложности одной из самых простых операций - вставки нового элемента.

Условия анализа будут следующими: включаемый элемент является новым, т. е. элемента с таким значением информационного поля еще нет в дереве; рассматриваются два вида деревьев - идеальное, имеющее n = 2^k-1 вершин, и вырожденное (линейный список).

1. Идеальное дерево. В этом дереве все вершины располагаются на k уровнях: корень на первом уровне, две вершины на втором уровне, четыре вершины на третьем уровне,..., 2^k-1 вершины на k уровне. Новая вершина может быть помещена только на (k+1) -й уровень, для этого нужно определить, к какой ветви вершина будет подсоединена. Проверка начинается с корня. Сравнение информационных полей корня и новой вершины отвечает на вопрос, в каком поддереве, левом или правом, должна быть размещена новая вершина. После сравнения следует переход по ветви к корню соответствующего поддерева или, если ветвь уже закончилась, размещение новой вершины в конце ветви. Поскольку все ветви в идеальном дереве имеют одинаковую длину (содержат k вершин), то, считая элементарным шагом действие "сравнить информационные поля вершин и, либо перейти по ссылке к следующей вершине, либо разместить новую вершину", можно оценить сложность вставки величиной k =log₂(n+1). Причем эта оценка одновременно является и максимальной и средней, она также не зависит от значения информационного поля нового элемента. 2. Вырожденное дерево. Это дерево представляет собой линейный список элементов, упорядоченных по возрастанию или убыванию значений информационных полей. Длина списка равна n и количество элементарных шагов (таких же, как и для идеального дерева) зависит на этот раз от включаемого элемента. Для определенности рассмотрим дерево, состоящее только из правых поддеревьев (в дерево включались упорядоченные по возрастанию элементы). Различаются три случая:

1. новый элемент предшествует уже имеющимся, т. е. значение его информационного поля меньше значений информационных полей имеющихся в дереве вершин, в том числе корня; тогда новый элемент становится левым потомком корня, операция заканчивается за один шаг, дерево перестает быть вырожденным;
2. все имеющиеся в дереве элементы предшествуют новому; новый элемент должен стать правым потомком последней (самой правой) вершины, для этого требуется выполнить n элементарных шагов; дерево остается вырожденным;
3. новый элемент предшествует части вершин дерева, но другая часть вершин предшествует ему; в этом случае в списке имеется i -я вершина, левым потомком которой становится новый элемент; требуется выполнить i, 1<=i<=n, элементарных шагов, дерево перестает быть вырожденным.

В случае (в) максимальная оценка сложности равна n, а средняя зависит от того, каким является множество, из которого выбираются значения информационных полей элементов, какое распределение имеет выборка из n значений, уже помещенных в дерево, и каково вероятностное распределение, из которого было выбрано значение информационного поля нового элемента. За неимением подробных сведений об этом обычно берут среднюю оценку в виде (n+1)/2.

Таким образом, получаем оценки от log₂(n+1) для лучших деревьев до n для худших деревьев при одинаковом количестве вершин n. Ясно, что максимальная оценка сложности включения элемента в произвольное дерево определяется худшим случаем. Со средней оценкой дело обстоит иначе. Усреднение должно быть произведено не только по характеристикам вновь включаемого элемента (как в случае "в"), но и по всевозможным деревьям. Поэтому следующим этапом является анализ того, как часто встречаются хорошие и плохие деревья.

Напомним, что если имеется идеальное дерево с n = 2^k-1 вершинами, где k - количество уровней, то для присоединения к этому дереву нового элемента потребуется в точности k элементарных шагов (сравнений и переходов по указателю). Сколько потребуется элементарных шагов для отыскания элемента в идеальном дереве? Ответ на этот вопрос зависит от того, какие вершины к настоящему моменту имеются в дереве (каковы значения их информационных полей), и какую информацию мы ищем. Обычно, раздельно рассматривают 2 случая:

• информационное поле искомого элемента имеет значение, заведомо отсутствующее в дереве, так называемый неудачный поиск;
• искомый элемент присутствует в дереве, так называемый удачный поиск.

В первом случае количество сравнений такое же, как и при включении нового элемента, т. е. k, а количество переходов на единицу меньше.

Второй случай требует более подробного анализа. Предположим, что искомая вершина с равной вероятностью находится в любой из позиций идеального дерева. Время ее поиска однозначно определяется номером уровня, на котором эта вершина находится. Если это 1-й уровень (корень), то достаточно одного сравнения, если k -й уровень (одна из висячих вершин), то требуется максимальное количество сравнений - k. Таким образом, количество сравнений с_n является случайной величиной, принимающей значения из интервала [1, k]. Осталось выяснить, какова вероятность p_i, того, что с_n примет значение i.

Очевидно, что, приняв условие равновероятности вершин при поиске, необходимо сделать вывод: вероятность попадания на некоторый уровень пропорциональна количеству вершин на этом уровне. Поскольку на каком-то из уровней искомая вершина обязательно находится, т. е. сумма вероятностей равна единице, то вероятность нахождения искомой вершины на i -м уровне равна отношению количества вершин i -го уровня к общему количеству вершин дерева:

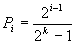
Среднее количество сравнений (математическое ожидание) равно:

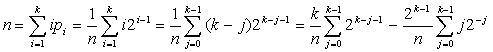
Первое слагаемое равно k, а для вычисления второго слагаемого можно использовать известную формулу:

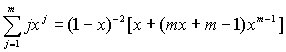
Таким образом, после преобразований получаем выражение:

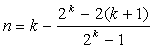
Так как нас интересуют достаточно грубые оценки, то при больших k мы можем считать значение дроби приблизительно равным единице. Тогда n = k-1. Следовательно, максимальная и средняя сложность поиска информации в идеальном дереве почти совпадают.

Поскольку различие в сложности включения нового элемента в идеальное дерево и в дерево вырожденное значительно отличаются, а заранее не известно, какие деревья у нас будут получаться, то интересно найти ответы на следующие вопросы.

1. Сколько существует различных бинарных деревьев с n вершинами?
2. Сколько среди них вырожденных и как часто они возникают?
3. Сколько среди деревьев идеальных или близких к идеальным, какие последовательности значений их порождают?

Ответы на эти вопросы важны потому, что если большинство деревьев - вырожденные, то деревья почти не имеют преимуществ перед списками, а недостаток очевиден - для деревьев требуется больше памяти. Если же большинство деревьев близки к идеальным, то дерево как структура данных для хранения информации имеет большое значение и стоит приложить усилия к совершенствованию процедур работы с деревьями (например, чтобы совсем исключить появление вырожденных деревьев).

На следующем шаге мы рассмотрим число бинарных деревьев.

На этом шаге мы рассмотрим число бинарных деревьев.

Число бинарных деревьев определяется, исходя из рекурсивного определения бинарного дерева: число деревьев с n вершинами определяется как сумма чисел возможных комбинаций левых и правых поддеревьев. Это дает возможность составить уравнения, решение которых и дает искомое число.

Обозначим t_n - число различных бинарных деревьев, содержащих n вершин. Под различными деревьями мы понимаем в том числе учет свойства вершины быть левым или правым потомком. Таким образом, симметричные деревья, изоморфные с точки зрения теории графов, являются различными. Например, вырожденные деревья, представляющие собой цепи левых и правых потомков - различны с нашей точки зрения, хотя и изоморфны. Имеет место формула:

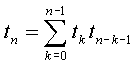
которую можно объяснить следующим образом.

Пусть t_k обозначает количество возможных левых поддеревьев, содержащих k вершин, t_n-k-1 - количество соответствующих правых поддеревьев, содержащих n-k-1 вершину (k вершин в левом поддереве и одна вершина - корень). Левое поддерево может быть пустым, разумеется, существует только один вариант пустого дерева, т. е. t₀=1. При этом в правом поддереве n-1 вершина и имеется t n способ построить такое дерево. Общее количество способов построить дерево, сохраняя заданное соотношение количеств вершин в левом и правом поддеревьях k и n-k-1, равно t_kt_n-k-1. Суммируя по всем возможным значениям k, получаем количество t_n деревьев с n вершинами.

Приведенное равенство можно использовать для итерационного вычисления количества деревьев, начиная с деревьев, содержащих одну вершину:

t₁ = t₀ = 1,

t₂ = t₁t₀ + t₀t₁ = 2,

t₃ = t₀t₂ + t₁t₁ + t₂t₀ = 5 и т.д.

В частности, t₄ = 14, t₅ = 42, t₆ = 132, t₇ = 429. Таким способом можно вычислить количество бинарных деревьев с любым числом вершин, но сложность и громоздкость вычислений возрастают с ростом n. Хотелось бы получить результат в виде явной зависимости t_n от параметра n без использования значений t_n-i.

Для этого используется производящая функция 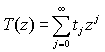членов последовательности {t_n}, где z - некая формальная переменная. Отыскивается она следующим образом. Вместо суммы для t_n запишем сумму для t_n+1:

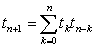
Правая часть принимает классический вид свертки двух последовательностей (в данном случае - это свертка последовательности {t_n} с самой собой) и ее производящая функция равна Т₁(z) в соответствии с теорией z -преобразований. Левая часть задает член последовательности {t_n+1}, сдвинутой относительно последовательности {t_n} на одну позицию и ее производящая функция по правилам z -преобразований может быть определена как (T(z) - t₀)z. Получили уравнение:

(T(z)-t₀) z^-1 =T²(z)

для определения неизвестной функции T(z), которое имеет решение:

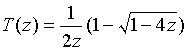
Разложение его в ряд по степеням z в районе точки z = 0 имеет вид:

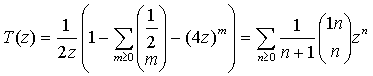
Таким образом,

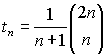
На следующем шаге мы рассмотрим число вырожденных деревьев.

На этом шаге мы рассмотрим число вырожденных деревьев.

Вырожденное дерево - это линейный список. Мы уже приводили примеры вырожденных деревьев: список левых потомков и список правых потомков. Но это не единственные вырожденные деревья. Условием вырожденности дерева является наличие у любой вершины, кроме последней, только одного потомка. На рисунке 1 приведены все возможные вырожденные деревья для n = 4.

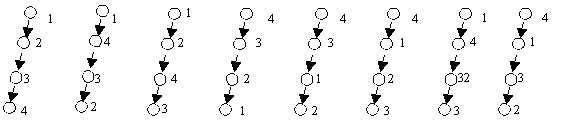
Рис.1. Примеры вырожденных деревьев

Идеальные деревья

Как уже ясно, при данном n = 2^k-1 существует только одно идеальное бинарное дерево. Это должно обескураживать. Ведь вырожденных деревьев с тем же количеством вершин 2^(n-1). Значит ли это, что плохие деревья встречаются чаще, чем хорошие?

Анализ ситуации основан на анализе последовательностей значений и на том, какие деревья порождаются последовательностями. Как известно, имеется n! различных последовательностей (перестановок) из n чисел. Это значительно больше, чем количество:

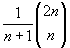
деревьев с n вершинами. Следовательно, некоторые перестановки порождают одинаковые деревья. В связи с единственностью идеального дерева вопрос должен быть сформулирован так: сколько различных последовательностей чисел при помещении этих чисел в бинарное дерево порождают идеальное дерево? Именно отношение числа таких последовательностей к общему числу различных последовательностей (n!) и характеризуют частоту появления идеальных деревьев.

Конкретная последовательность диктует трассу алгоритма построения дерева. Все множество последовательностей, порождающих идеальные деревья, можно разделить на группы (подмножества) по типам трасс. Например, можно выделить группу последовательностей, строящих дерево по уровням: вершины не включаются в (i + 1) -й уровень, пока не завершен i -й уровень.

Другая группа - заполнение дерева сначала левого поддерева, а затем правого и т. д. - непересекающихся групп может быть выделено очень много (две последовательности отличаются, если в них изменен порядок хотя бы двух чисел).

Оценим количество последовательностей в первой группе - последовательностей, заполняющих дерево по уровням. Поскольку не для любого n существует идеальное дерево будем рассматривать только значения n = 2^k-1. Пусть даны n различных чисел, которые нужно поместить в дерево. Их конкретные значения не влияют на анализ, но для определенности возьмем числа 1, 2, 3,..., n. Каждое из них имеет определенное место в идеальном дереве, например, в четырехуровневом дереве при n = 15 (рисунок 2).

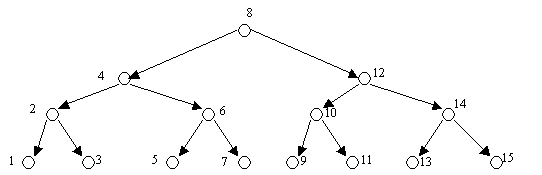
Рис.2. Идеальное четырехуровневое дерево

Любая последовательность чисел 1, 2, 3,..., 15 должна начинаться с 8, иначе построить дерево не удастся. Вторым членом последовательности может быть 4 или 12, третьим членом - то из двух чисел, которое не было выбрано в качестве второго члена. Четвертым членом может быть любое из чисел 2, 6, 10, 14, пятым - любое из трех, не выбранных в качестве четвертого и т. д.

Рассматривая заполнение по уровням, можно заметить, что:

• на первом уровне выбора нет - имеется только одно число, 2^(k-1), которое должно стать корнем;
• на втором уровне имеется 2 вершины и 2! возможностей выбора второго и третьего элементов последовательности;
• на третьем уровне 4 вершины и 4! возможностей выбора четвертого... седьмого элементов последовательности;
• на k -м уровне 2_(k-1) вершин и 2^(k-1)! возможностей выбора "хвоста" последовательности.

Таким образом, общее количество вариантов построения последовательностей чисел, приводящих к идеальному графу при поуровневом заполнении, равно:

(2⁰)! (2¹)! (2²)! (2³)!... (2^k-1)!

При k=2, n=3 имеется 2! = 2 последовательности поуровневого заполнения и это единственные последовательности, приводящие к идеальному дереву. Заметим, что вырожденных деревьев получается больше - 4. При k = 3, n = 7 получаем 1! 2! 4! = 48 последовательностей (общее количество последовательностей, приводящих к идеальному графу любыми способами, равно 80 - найдено прямым подсчетом). Вырожденных деревьев - 64.

Картина резко меняется при дальнейшем увеличении n. Четыре уровня, n = 15: вырожденных деревьев - 34768; идеальных последовательностей - 1935360. Пять уровней, n = 31: вырожденных деревьев - 2147483648 ~ 2,15*10⁹; количество идеальных последовательностей 1,9*10²¹.

Два последних примера показывают, что идеальные деревья могут встречаться гораздо чаще, чем вырожденные. Чтобы показать, что для достаточно больших n это всегда так, оценим отношение частот их появления; причем частоту появления идеальных деревьев оценим снизу, используя количество последовательностей, строящих дерево по уровням. Чуть менее громоздко формула будет выглядеть, если взять логарифм отношения частот. Факториалы, встречающиеся в формулах, заменим приближенными выражениями по формуле Стирлинга:

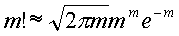
Тогда логарифм отношения частот равен:

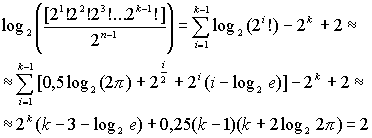
В выводе последней формулы для упрощения выражения некоторые конечные суммы (геометрической прогрессии и др.) заменены бесконечными, что, учитывая быструю сходимость соответствующих рядов, дает относительно небольшую ошибку.

Из этой формулы видно, что при k > 4 значение логарифма отношения частот положительно и, следовательно, идеальные деревья встречаются чаще вырожденных. Более того, знач