Магнитное поле постоянных токов различной формы изучалось французскими учеными Ж. Био (1774–1862) и Ф. Саваром (1791–1841). Результаты этих опытов были обобщены выдающимся французским математиком и физиком П. Лапласом.
Закон Био-Савара-Лапласа для проводника с током 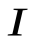 , элемент
, элемент 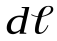 которого создает в некоторой точке
которого создает в некоторой точке 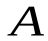 (рис. 1) индукцию поля
(рис. 1) индукцию поля 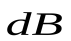 , записывается в виде:
, записывается в виде:
 , (1.3)
, (1.3)
где  – вектор, по модулю равный длине
– вектор, по модулю равный длине 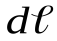 элемента проводника и совпадающий по направлению с током;
элемента проводника и совпадающий по направлению с током; 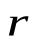 – радиус-вектор, проведенный из элемента
– радиус-вектор, проведенный из элемента 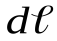 проводника в точку
проводника в точку  исследуемого поля,
исследуемого поля,  – модуль радиуса-вектора
– модуль радиуса-вектора 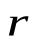 ;
; 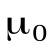 –магнитная постоянная (
–магнитная постоянная ( );
); 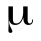 – магнитная проницаемость среды, которая в воздухе и в вакууме равна единице. Направление
– магнитная проницаемость среды, которая в воздухе и в вакууме равна единице. Направление  перпендикулярно
перпендикулярно  и
и 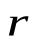 , т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление
, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу нахождения линий магнитной индукции (правилу правого винта): направление вращения головки винта дает направление  , если поступательное движение винта соответствует направлению тока в элементе.
, если поступательное движение винта соответствует направлению тока в элементе.
М  одуль вектора
одуль вектора  определяется выражением
определяется выражением
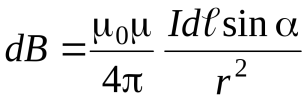 , (1.4)
, (1.4)
где  – угол между векторами
– угол между векторами  и
и 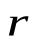 .
.
Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
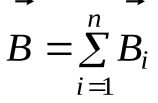 . (1.5)
. (1.5)
Расчет характеристик магнитного поля (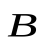 и
и 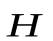 ) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био-Савара-Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля. Рассмотрим два примера.
) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био-Савара-Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля. Рассмотрим два примера.
М 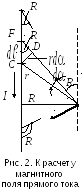 агнитное поле прямого тока, текущего по тонкому прямому проводу бесконечной длины (рис. 2). В произвольной точке
агнитное поле прямого тока, текущего по тонкому прямому проводу бесконечной длины (рис. 2). В произвольной точке  ,удаленной от оси проводника на расстояние
,удаленной от оси проводника на расстояние 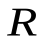 , векторы
, векторы  от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов
от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа («к нам»). Поэтому сложение векторов  можно заменить сложением их модулей. В качестве переменной интегрирования выберем угол
можно заменить сложением их модулей. В качестве переменной интегрирования выберем угол  (угол между векторами
(угол между векторами  и
и 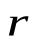 ), выразив через него все остальные величины. Из рис. 2 следует:
), выразив через него все остальные величины. Из рис. 2 следует:

(радиус дуги CD вследствие малости  равен
равен 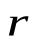 , и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (1.4), получим, что магнитная индукция, создаваемая одним элементом проводника, будет следующая
, и угол FDC по этой же причине можно считать прямым). Подставив эти выражения в (1.4), получим, что магнитная индукция, создаваемая одним элементом проводника, будет следующая

 . (1.6)
. (1.6)
Так как угол  для всех элементов прямого тока бесконечно длинного изменяется в пределах от 0 до
для всех элементов прямого тока бесконечно длинного изменяется в пределах от 0 до  , согласно (1.5) и (1.6) получим:
, согласно (1.5) и (1.6) получим:
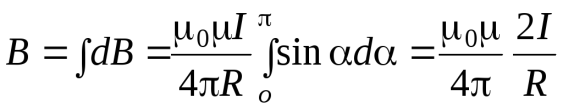 .
.
Следовательно, магнитная индукция поля прямого тока бесконечной длины
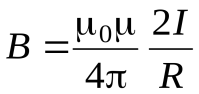 . (1.7)
. (1.7)
Если проводник конечной длины, то  меняется от
меняется от 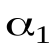 до
до 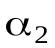 (рис. 2) и тогда интегрируя (1.6), получим
(рис. 2) и тогда интегрируя (1.6), получим
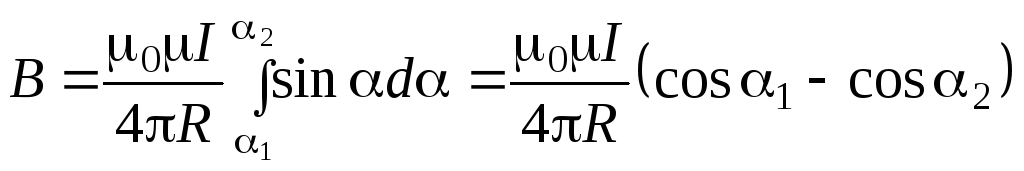 . (1.8)
. (1.8)
Магнитное поле в центре кругового проводника с током. Все элементы кругового проводника с током создают в центре магнитные поля одинакового направления – вдоль нормали от витка. Поэтому сложение векторов 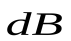 можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (
можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору ( ) и расстояние всех элементов проводника до центра кругового тока одинаково и равно
) и расстояние всех элементов проводника до центра кругового тока одинаково и равно 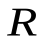 , то согласно (1.4):
, то согласно (1.4):
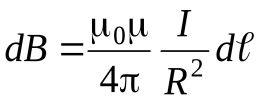 .
.
Тогда
 .
.
Следовательно, магнитная индукция поля в центре кругового проводника с током имеет вид:
 .
.
Эту силу называют силой Лоренца. Угол α в этом выражении равен углу между скоростью  и вектором магнитной индукции
и вектором магнитной индукции 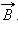 Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика. Взаимное расположение векторов
Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика. Взаимное расположение векторов  ,
,  и
и 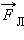 для положительно заряженной частицы показано на рис. 1.18.1.
для положительно заряженной частицы показано на рис. 1.18.1.

|
Рисунок 1.18.1.
Взаимное расположение векторов  , ,  и и  Модуль силы Лоренца Модуль силы Лоренца 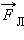 численно равен площади параллелограмма, построенного на векторах численно равен площади параллелограмма, построенного на векторах  и и 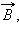 помноженной на заряд q помноженной на заряд q
|
Сила Лоренца направлена перпендикулярно векторам  и
и 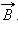
При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется.
Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость  лежит в плоскости, перпендикулярной вектору
лежит в плоскости, перпендикулярной вектору 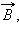 то частица будет двигаться по окружности радиуса
то частица будет двигаться по окружности радиуса
Сила Лоренца в этом случае играет роль центростремительной силы (рис. 1.18.2).
Выражение для силы Лоренца (114.1) позволяет найти ряд закономерностей движения заряженных частиц в магнитном поле. Направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле зависят от знака заряда Q частицы. На этом основано определение знака заряда частиц, движущихся в магнитных полях.
Для вывода общих закономерностей будем считать, что магнитное поле однородно и на частицы электрические поля не действуют. Если заряженная частица движется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол а между векторами v и В равен 0 или p. Тогда по формуле (114.1) сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно.
Если заряженная частица движется в магнитном поле со скоростью v, перпендикулярной вектору В, то сила Лоренца F =Q[ vB ] постоянна по модулю и нормальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центростремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус r которой определяется из условия
QvB = mv2/r,
откуда

Период вращения частицы, т. е. время Т, затрачиваемое ею на один полный оборот,
T = 2nr/v.
Подставив сюда выражение (115.1), получим
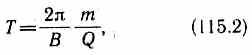
т. е. период вращения частицы в однородном магнитном поле определяется только величиной, обратной удельному заряду
(Q/m) частицы, и магнитной индукцией поля, но не зависит от ее скорости (при v << с)). На этом основано действие циклических ускорителей заряженных частиц (см. §116).
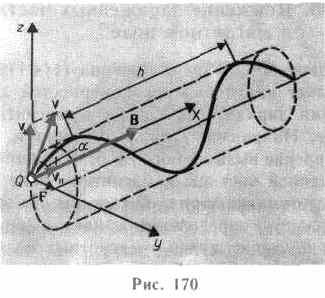
Если скорость v заряженной частицы направлена под углом а к вектору В (рис. 170), то ее движение можно представить в виде суперпозиции: 1) равномерного прямолинейного движения вдоль поля со скоростью v||=vcosa; 2) равномерного движения со скоростью v ┴= v sina по окружности в плоскости, перпендикулярной полю. Радиус окружности определяется формулой (115.1) (в данном случае надо заменить v на v┴=vsina). В результате сложения обоих движений возникает движение по спирали, ось которой параллельна магнитному полю (рис. 170). Шаг винтовой линии
h=v || T=vT cosa.
Подставив в последнее выражение (115.2), получим
h=2pmv cosa/(BQ).
Направление, в котором закручивается спираль, зависит от знака заряда частицы.
Если скорость v заряженной частицы составляет угол а с направлением вектора В неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, то r и h уменьшаются с ростом В. На этом основана фокусировка заряженных частиц в магнитном поле.
В) Частица движется со скоростью 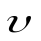 , направленной под произвольным острым углом
, направленной под произвольным острым углом 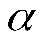 к вектору магнитной индукции
к вектору магнитной индукции 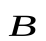 .
.
Разложим вектор 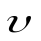 на две составляющие:
на две составляющие:
 параллельна вектору
параллельна вектору 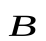 ;
;
 перпендикулярна вектору
перпендикулярна вектору 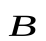 .
.
Скорость  в магнитном поле не изменяется.
в магнитном поле не изменяется.
Частица одновременно участвует в двух движениях: она равномерно вращается со скоростью 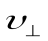 по окружности радиуса r и движется поступательно с постоянной скоростью
по окружности радиуса r и движется поступательно с постоянной скоростью  в направлении, перпендикулярном плоскости вращения. Траектория заряженной частицы представляет собой винтовую линию, ось которой совпадает с линией вектора
в направлении, перпендикулярном плоскости вращения. Траектория заряженной частицы представляет собой винтовую линию, ось которой совпадает с линией вектора 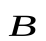 . Шаг винтовой линии (расстояние между витками):
. Шаг винтовой линии (расстояние между витками):  .
.
Для нерелятивистской частицы  и
и 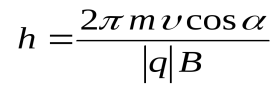 ;
;
Для релятивистской частицы 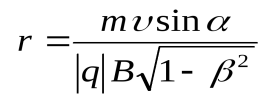 и
и  .
.
Циркуляцией вектора В по заданному замкнутому контуру называется интеграл
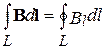 , (9.1)
, (9.1)
где d l – вектор элементарной длины контура, направленной вдоль обхода контура, Вl = В cosα– составляющая вектора В в направлении касательной к контуру (с учетом выбранного направления обхода), α – угол между векторами В и d l.
Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В): циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной μ о на алгебраическую сумму токов охватываемых этим контуром:
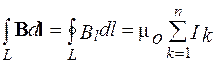 , (9.2)
, (9.2)
 где n – число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления считается отрицательным.
где n – число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления считается отрицательным.
Например, для системы токов, изображенных на рис.12, 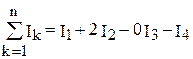 .
.
Выражение (9.2) справедливо только для поля в вакууме, поскольку для поля в веществе
Рис.12. необходимо согласно вышеизложенной гипотезе Ампера, учитывать микротоки (молекулярные токи).
Закон полного тока для магнитного поля в веществе является обобщением вышеприведенного закона с учетом как макротоков, так и микротоков:

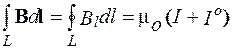 , (9.3)
, (9.3)
где I и Iо – соответственно алгебраические суммы сил макротоков (токов проводимости) и микротоков, охватываемых заданных контуром. Таким образом, циркуляция вектора магнитной индукции В по замкнутому контуру равна алгебраической сумме токов проводимости и молекулярных токов, охватываемых этим контуром, умноженной на магнитную постоянную. Вектор В, характеризует результирующее поле микро- и макротоков и поэтому линии вектора магнитной индукции не имеют источников и являются замкнутыми.
Как показывает (1.4), магнитное поле макротоков описывается вектором напряженности Н, (В = μ о μ Н). Следовательно, циркуляция вектора напряженности Н магнитного поля равна алгебраической сумме сил токов проводимости, охватываемых этим контуром
 . (9.4)
. (9.4)
Это выражение представляет собой теорему о циркуляции вектора Н.
Между циркуляции векторов Е и В существует принципиальное различие. Циркуляция вектора Е электростатического поля всегда равна нулю, т.е. электростатическое поле является потенциальным. Циркуляции векторов В и Н магнитного поля нулю не равны. Такое поле называется вихревым, непотенциальным. Следовательно магнитное поле непотенциально.



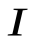 , элемент
, элемент 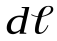 которого создает в некоторой точке
которого создает в некоторой точке 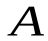 (рис. 1) индукцию поля
(рис. 1) индукцию поля 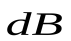 , записывается в виде:
, записывается в виде: , (1.3)
, (1.3) – вектор, по модулю равный длине
– вектор, по модулю равный длине 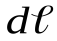 элемента проводника и совпадающий по направлению с током;
элемента проводника и совпадающий по направлению с током; 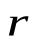 – радиус-вектор, проведенный из элемента
– радиус-вектор, проведенный из элемента  исследуемого поля,
исследуемого поля,  – модуль радиуса-вектора
– модуль радиуса-вектора 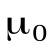 –магнитная постоянная (
–магнитная постоянная ( );
); 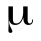 – магнитная проницаемость среды, которая в воздухе и в вакууме равна единице. Направление
– магнитная проницаемость среды, которая в воздухе и в вакууме равна единице. Направление  перпендикулярно
перпендикулярно  одуль вектора
одуль вектора 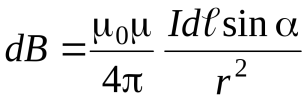 , (1.4)
, (1.4) – угол между векторами
– угол между векторами 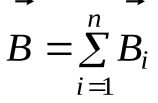 . (1.5)
. (1.5)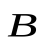 и
и 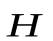 ) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био-Савара-Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля. Рассмотрим два примера.
) по приведенным формулам в общем случае сложен. Однако если распределение тока имеет определенную симметрию, то применение закона Био-Савара-Лапласа совместно с принципом суперпозиции позволяет просто рассчитать конкретные поля. Рассмотрим два примера.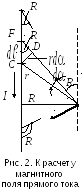 агнитное поле прямого тока, текущего по тонкому прямому проводу бесконечной длины (рис. 2). В произвольной точке
агнитное поле прямого тока, текущего по тонкому прямому проводу бесконечной длины (рис. 2). В произвольной точке 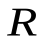 , векторы
, векторы 

 . (1.6)
. (1.6) для всех элементов прямого тока бесконечно длинного изменяется в пределах от 0 до
для всех элементов прямого тока бесконечно длинного изменяется в пределах от 0 до  , согласно (1.5) и (1.6) получим:
, согласно (1.5) и (1.6) получим: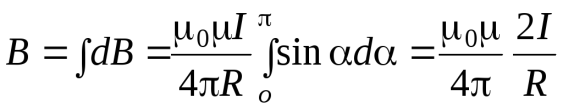 .
.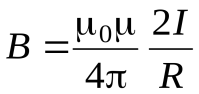 . (1.7)
. (1.7)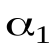 до
до 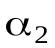 (рис. 2) и тогда интегрируя (1.6), получим
(рис. 2) и тогда интегрируя (1.6), получим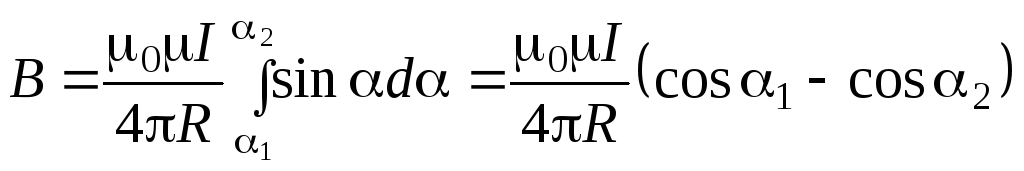 . (1.8)
. (1.8) ) и расстояние всех элементов проводника до центра кругового тока одинаково и равно
) и расстояние всех элементов проводника до центра кругового тока одинаково и равно 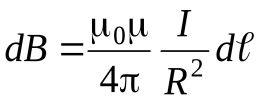 .
. .
. .
. и вектором магнитной индукции
и вектором магнитной индукции 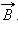 Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика. Взаимное расположение векторов
Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика. Взаимное расположение векторов  и
и 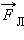 для положительно заряженной частицы показано на рис. 1.18.1.
для положительно заряженной частицы показано на рис. 1.18.1.
 Модуль силы Лоренца
Модуль силы Лоренца 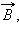 помноженной на заряд q
помноженной на заряд q
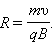

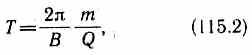

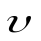 , направленной под произвольным острым углом
, направленной под произвольным острым углом 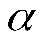 к вектору магнитной индукции
к вектору магнитной индукции 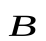 .
. параллельна вектору
параллельна вектору  перпендикулярна вектору
перпендикулярна вектору  в магнитном поле не изменяется.
в магнитном поле не изменяется.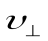 по окружности радиуса r и движется поступательно с постоянной скоростью
по окружности радиуса r и движется поступательно с постоянной скоростью  .
. и
и 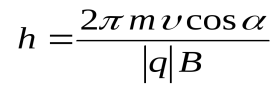 ;
;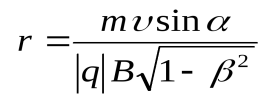 и
и  .
.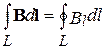 , (9.1)
, (9.1)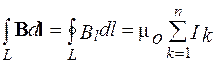 , (9.2)
, (9.2) где n – число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления считается отрицательным.
где n – число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта; ток противоположного направления считается отрицательным.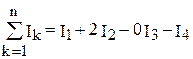 .
.
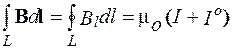 , (9.3)
, (9.3) . (9.4)
. (9.4)


