Иванов В.И.
профессор, д.ф.-м.н.
КОНСПЕКТ ЛЕКЦИЙ
по дисциплине
Математический анализ
(Часть 4)
Направление подготовки: 010400 «Прикладная математика и информатика»
Профиль подготовки: «Прикладная математика и информатика»
Форма обучения: очная
Тула 2013 г.
Рассмотрено на заседании кафедры
протокол № 1 от 02 сентября 2013 г.
Зав. кафедрой________________В.И. Иванов
СОДЕРЖАНИЕ
ЛЕКЦИЯ 1. Поточечная и равномерная сходимости функциональной последовательности и функционального ряда. Критерий Коши равномерной сходимости. Признаки Вейерштрасса, Абеля, Дирихле равномерной сходимости функционального ряда. 4
ЛЕКЦИЯ 2. Равномерная сходимость и непрерывность предельной функции функциональной последовательности и суммы функционального ряда. Пространство  . Его полнота. 9
. Его полнота. 9
ЛЕКЦИЯ 3. Равномерная сходимость и интегрируемость предельной функции функциональной последовательности и суммы функционального ряда. 11
ЛЕКЦИЯ 4. Равномерная сходимость и дифференцируемость предельной функции функциональной последовательности и суммы функционального ряда. Пространство 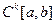 . Его полнота. 13
. Его полнота. 13
ЛЕКЦИЯ 5. Степенные ряды. Поточечная сходимость. Радиус и интервал сходимости. Формула Коши-Адамара. 14
ЛЕКЦИЯ 6. Равномерная сходимость степенного ряда. Свойства суммы степенного ряда. 16
ЛЕКЦИЯ 7. Ряд Тейлора. Единственность разложения функции в степенной ряд. Достаточное условие разложимости. Ряд Тейлора-Маклорена для функций  ................................................... 18
................................................... 18
ЛЕКЦИЯ 8. Собственные интегралы, зависящие от параметра. Теоремы о его непрерывности, интегрируемости и дифференцируемости. 20
ЛЕКЦИЯ 9. Равномерная сходимость несобственного интеграла, зависящего от параметра. Критерий Коши. Признаки Вейерштрасса, Абеля, Дирихле. 22
ЛЕКЦИЯ 10. Теоремы о непрерывности, интегрируемости и дифференцируемости несобственного интеграла, зависящего от параметра. 26
ЛЕКЦИЯ 11. Гамма и бета-функция Эйлера. Формула Стирлинга. 28
ЛЕКЦИЯ 12. Евклидово пространство интегрируемых функций. Ортонормированная система. Задача о наилучшем приближении элемента евклидова пространства по ортонормированной системе. Базисность и замкнутость ортонормированной системы. Ряд и коэффициенты Фурье. Неравенство Бесселя и равенство Парсеваля. 34
ЛЕКЦИЯ 13. Тригонометрическая система. Ее замкнутость. Тригонометрические ряды Фурье интегрируемых функций. Сходимость в среднеквадратичном. Равенство Парсеваля. 38
ЛЕКЦИЯ 14. Тригонометрические ряды Фурье непрерывных функций. Частичные суммы. Ядро Дирихле. Отсутствие равномерной сходимости. Достаточное условие равномерной сходимости. 43
ЛЕКЦИЯ 15. Равномерная сходимость средних Фейера для непрерывных функций. Теоремы Вейерштрасса о равномерном приближении непрерывных функций тригонометрическими полиномами и алгебраическими многочленами. Теорема Стоуна-Вейерштрасса. 46
ЛЕКЦИЯ 16. Достаточное условие поточечной сходимости тригонометрического ряда Фурье. 50
ЛЕКЦИЯ 17. Преобразование Фурье. Косинус и синус преобразования Фурье. Свойства преобразования Фурье. Обратное преобразование Фурье. 54
ЛЕКЦИЯ 1
Поточечная и равномерная сходимости функциональной последовательности и функционального ряда. Критерий Коши равномерной сходимости. Признаки Вейерштрасса, Абеля, Дирихле равномерной сходимости функционального ряда
1. Поточечная и равномерная сходимости функциональной последовательности и функционального ряда
Сумма геометрической прогрессии  сходится и определяет новую функцию. Это есть пример функционального ряда.
сходится и определяет новую функцию. Это есть пример функционального ряда.
Пусть 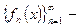 последовательность функций, определённых на одном и том же множестве
последовательность функций, определённых на одном и том же множестве 
Функциональный ряд – это ряд вида  .
.
Определим область сходимости (поточечной сходимости) для функциональной последовательности и функционального ряда:  предельная функция. Аналогично для функционального ряда
предельная функция. Аналогично для функционального ряда  область сходимости (поточечной сходимости) функционального ряда, а
область сходимости (поточечной сходимости) функционального ряда, а  сумма функционального ряда.
сумма функционального ряда.
Нас будут интересовать следующие три задачи.
Задача 1. Пусть последовательность функций  . Когда
. Когда  .
.
 Примеры. Пусть
Примеры. Пусть  .
.
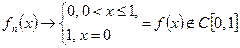 .
.
Аналогичную задачу можно поставить и для функционального ряда.
 Пример.
Пример.  .
.
Задача 2. Пусть 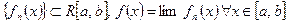 (R – интегрируема). Когда можно гарантировать, что
(R – интегрируема). Когда можно гарантировать, что  или
или  .
.


 .
.
Задача 3. Пусть  (С1- непрерывно дифференцируема). Когда
(С1- непрерывно дифференцируема). Когда  , или
, или  .
.
Пример. 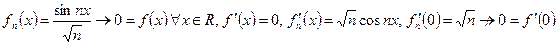 .
.
Итак, в результате поточечной сходимости предельная функция не наследует хорошие свойства функции последовательности. Необходимо усиление поточечной сходимости. Таким усилением будет равномерная сходимость.
Равномерная сходимость последовательности функций и функционального ряда
Вначале проанализируем условие поточечной сходимости последовательности функций на отрезке:  на
на  .
.
Будем говорить, что последовательность  равномерно сходится на
равномерно сходится на  к f(x), т.е.
к f(x), т.е.  , если
, если 
 .
.
Пусть  , тогда эквивалентное определение равномерной сходимости выглядит так:
, тогда эквивалентное определение равномерной сходимости выглядит так:  .
.
Ряд  называется равномерно сходящимся к своей сумма на [ a, b ], если его последовательность частичных сумм сходится равномерно на [ a, b ] к S(x), т.е.
называется равномерно сходящимся к своей сумма на [ a, b ], если его последовательность частичных сумм сходится равномерно на [ a, b ] к S(x), т.е. 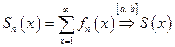 или
или

Из равномерной сходимости вытекает поточечная сходимость, а обратное - неверно. Рассмотрим примеры.
Пример 1. 
 , т.е. поточечная сходимость есть, а равномерной сходимости нет.
, т.е. поточечная сходимость есть, а равномерной сходимости нет.
Пример 2.


т.е. равномерной сходимости нет.
Пример 3.
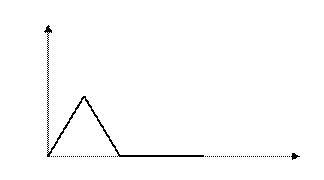
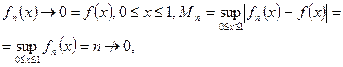
т.е. равномерной сходимости нет.
Пример 4. 
 т.е. равномерная сходимость есть, но и в этом случае её недостаточно.
т.е. равномерная сходимость есть, но и в этом случае её недостаточно.
2. Критерий Коши равномерной сходимости. Признак Вейерштрасса равномерной сходимости функционального ряда
Критерий Коши.
 , или
, или  .
.
Критерий Коши также называется равномерной фундаментальностью.
Доказательство. Необходимость.
Пусть  , тогда
, тогда

 равномерная фундаментальность последовательности fn(x).
равномерная фундаментальность последовательности fn(x).
Достаточность.
Пусть fn(x) – равномерная фундаментальная последовательность Þ fn(x) – фундаментальная  (по критерию Коши)
(по критерию Коши)  . Запишем подробно условие равномерной фундаментальности:
. Запишем подробно условие равномерной фундаментальности: 
 .
.
Доказано.
Для функционального ряда критерий Коши выглядит так:  равномерно сходится на [ a, b ] тогда и только тогда, когда последовательность частичных сумм Sn(x) равномерно фундаментальная на [ a, b ], т.е.
равномерно сходится на [ a, b ] тогда и только тогда, когда последовательность частичных сумм Sn(x) равномерно фундаментальная на [ a, b ], т.е.  .
.
Пример. 
Применим критерий Коши: 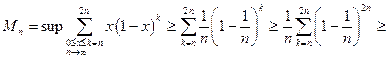
 равномерной сходимости нет.
равномерной сходимости нет.
Для равномерной сходимости функционального ряда можно указать некоторые достаточные признаки.
Признак Вейерштрасса.
Если 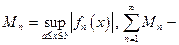 сходится, то
сходится, то  сходится равномерно на [ a, b ].
сходится равномерно на [ a, b ].
Доказательство. Будем использовать критерий Коши для равномерной сходимости функционального ряда. 

(по критерию Коши) 
Доказано.
Пример. 

поэтому при  по признаку Вейерштрасса функциональный ряд сходится равномерно для всех
по признаку Вейерштрасса функциональный ряд сходится равномерно для всех  , хотя поточечно он сходится при
, хотя поточечно он сходится при  .
.
При  можно показать, что для ряда
можно показать, что для ряда  справедливо следующее важное утверждение: частичные суммы ряда
справедливо следующее важное утверждение: частичные суммы ряда  равномерно ограничены для любого х:
равномерно ограничены для любого х: 

Доказательство. В силу периодичности и нечётности достаточно считать и рассмотреть 
Для оценки  воспользуемся преобразованием Абеля:
воспользуемся преобразованием Абеля:

Далее:

Итак, 
3. Признаки Абеля, Дирихле равномерной сходимости функционального ряда
Сформулируем признаки равномерной сходимости Дирихле и Абеля для рядов вида:  (1).
(1).
Признак Дирихле.
Если для ряда (1) выполнены условия:
1) 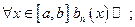
2) 
3) 
то ряд (1) сходится равномерно на [ a, b ].
Признак Абеля.
Если для ряда (1) выполнены условия:
1) 
2) 
3) 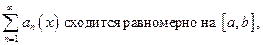 то ряд (1) сходится равномерно на
то ряд (1) сходится равномерно на 
Эти признаки доказываются точно также как и для числовых рядов, используя преобразование Абеля и критерий Коши для сходящихся рядов.
Задача. При каких условиях на  (невозрастающая)
(невозрастающая) 
Достаточные условия вытекают из признака Дирихле:

Остаётся проанализировать условия (1) и (2) и потребовать, чтобы  Если эти условия выполнены, то ряд сходится равномерно. Можно показать, что эти условия являются и необходимыми.
Если эти условия выполнены, то ряд сходится равномерно. Можно показать, что эти условия являются и необходимыми.
ЛЕКЦИЯ 2
Равномерная сходимость и непрерывность предельной функции функциональной последовательности и суммы функционального ряда. Пространство  . Его полнота
. Его полнота
1. Равномерная сходимость и непрерывность предельной функции функциональной последовательности
Теорема 1. Если 
Доказательство. Будем исходить из следующей оценки:

Итак, 
 Зафиксируем
Зафиксируем  функция
функция 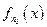 Î
Î
 равномерно непрерывна на [ a, b ]
равномерно непрерывна на [ a, b ] 

равномерно непрерывна на [ a, b ].
Доказано.
2. Равномерная сходимость и непрерывность суммы функционального ряда
Теорема 1¢. Если  непрерывна, функциональный ряд
непрерывна, функциональный ряд  сходится к
сходится к  то
то 
Доказательство. Если  частичные суммы, то
частичные суммы, то  также непрерывны и равномерно сходятся к
также непрерывны и равномерно сходятся к 
Утверждение теоремы 1¢ вытекает из теоремы 1.
Доказано.
3. Пространство  . Его полнота
. Его полнота
Множество непрерывных функций на отрезке 
 - линейное пространство бесконечной размерности, в котором можно ввести норму
- линейное пространство бесконечной размерности, в котором можно ввести норму  для которой выполнены свойства:
для которой выполнены свойства:
1) 
2) 
3) 
Линейное пространство с нормой называется нормированным пространством.
Норма позволяет определить сходимость на [ a, b ]:

Последовательность функций называется фундаментальной, если 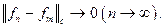 Нормированное пространство, в котором всякая фундаментальная последовательность является сходящейся, называется полным, или банаховым пространством (по имени С. Банаха).
Нормированное пространство, в котором всякая фундаментальная последовательность является сходящейся, называется полным, или банаховым пространством (по имени С. Банаха).
Отметим, что всякая сходящаяся последовательность является фундаментальной, т.е. в полном пространстве сходимость эквивалентна фундаментальности, или в полном пространстве выполнен критерий Коши.
Покажем, что нормированное пространство  является полным. Для этого рассмотрим сходимость в нём:
является полным. Для этого рассмотрим сходимость в нём:


Итак, сходимость по норме пространства  эквивалентна равномерной сходимости. Известно, что для равномерной сходимости выполнен критерий Коши. Это и означает, что пространство
эквивалентна равномерной сходимости. Известно, что для равномерной сходимости выполнен критерий Коши. Это и означает, что пространство  - полное.
- полное.
ЛЕКЦИЯ 3
ЛЕКЦИЯ 4
Равномерная сходимость и дифференцируемость предельной функции функциональной последовательности и суммы функционального ряда. Пространство 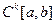 . Его полнота
. Его полнота
1. Равномерная сходимость и дифференцируемость предельной функции функциональной последовательности
Теорема 3. Если
1) 
2) 
3) 
то  также равномерно сходится к
также равномерно сходится к 
 .
.
Доказательство. Будем пользоваться следующими критерием:
 произвольное, а
произвольное, а 
Далее пользуясь критерием Коши, покажем равномерную сходимость последовательности 

равномерно по 
Далее:

Доказано.
2. Равномерная сходимость и дифференцируемость суммы
функционального ряда
Теорема 3¢. Если
1) 
2) 
3) 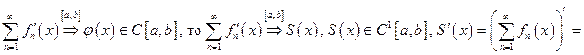

Доказательство. Если  то
то
1) 
2) 
3) 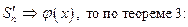

Доказано.
3. Пространство 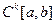 . Его полнота
. Его полнота
Пространство  - это множество
- это множество  раз непрерывно дифференцируемых на отрезке
раз непрерывно дифференцируемых на отрезке  функций. Это линейное пространство, в котором можно ввести норму
функций. Это линейное пространство, в котором можно ввести норму 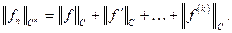
Охарактеризуем сходимость в этом пространстве:

т.е. сходимость по норме пространства  эквивалентна равномерной сходимости самой последовательности и последовательности её производных до порядка k включительно.
эквивалентна равномерной сходимости самой последовательности и последовательности её производных до порядка k включительно.
Отметим, что пространство  также является полным.
также является полным.
ЛЕКЦИЯ 5
ЛЕКЦИЯ 6
ЛЕКЦИЯ 7
Ряд Тейлора. Единственность разложения функции в степенной ряд. Достаточное условие разложимости. Ряд Тейлора-Маклорена для функций 
1. Ряд Тейлора. Единственность разложения функции в степенной ряд
Если функция раскладывается в степенной ряд (1) в некоторой окрестности точки а, то эта функция является бесконечно дифференцируемой в этой окрестности.
Пример. 
 непрерывна и имеет производные любого порядка и при
непрерывна и имеет производные любого порядка и при 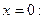
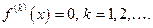

Производная в нуле: 

Теорема (о единственности разложения функции в степенной ряд). Если в некоторой окрестности точки а 
Степенной ряд вида  называется рядом Тейлора в окрестности точки а.
называется рядом Тейлора в окрестности точки а.
Таким образом, если функция раскладывается в степенной ряд, то он является рядом Тейлора. Например: 
Доказательство. 

Доказано.
Вернёмся к предыдущему примеру. Если ранее введённая функция раскладывается в степенной ряд в некоторой окрестности точки  противоречие с возможностью разложения некоторой функции в некоторой окрестности. Т.е. одной бесконечной дифференцируемости функции недостаточно для разложения в ряд.
противоречие с возможностью разложения некоторой функции в некоторой окрестности. Т.е. одной бесконечной дифференцируемости функции недостаточно для разложения в ряд.
2. Достаточное условие разложимости
Исследуем условия разложимости функции в степенной ряд. Для этого воспользуемся формулой Тейлора:

Отсюда, 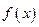 раскладывается в степенной ряд в точке а тогда и только тогда, когда:
раскладывается в степенной ряд в точке а тогда и только тогда, когда:
 Таким образом, вопрос о разложимости связан с ростом производных функции f. Укажем достаточные условия на рост производных для разложимости функций в степенной ряд.
Таким образом, вопрос о разложимости связан с ростом производных функции f. Укажем достаточные условия на рост производных для разложимости функций в степенной ряд.
Теорема. Если  то
то 
 .
.
Доказательство. Имеем

Убедимся, что  Удобнее всего для этого рассмотреть ряд
Удобнее всего для этого рассмотреть ряд  и доказать его сходимость По признаку Даламбера получаем:
и доказать его сходимость По признаку Даламбера получаем:
 ряд сходится, и в таком случае предел общего члена равен нулю.
ряд сходится, и в таком случае предел общего члена равен нулю.
Доказано.
3. Ряд Тейлора-Маклорена для элементарных функций

Последнее разложение получено почленным дифференцированием предыдущего разложения.


ЛЕКЦИЯ 8
ЛЕКЦИЯ 9
ЛЕКЦИЯ 10
ЛЕКЦИЯ 11
Доказательство.
1. Т.к. 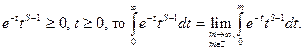
2. 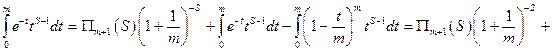
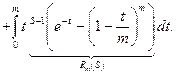
Из этого представления равенство (*) будет вытекать тогда и только тогда, когда 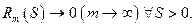
3. Введём вспомогательные неравенства.
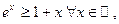
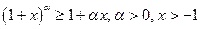 (неравенство Бернулли).
(неравенство Бернулли).
Докажем это неравенство методом математической индукции.
При 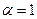 равенство очевидно.
равенство очевидно.
 верно.
верно.
4. Докажем, что 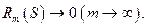
Докажем, что 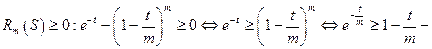 неравенство из 3. при
неравенство из 3. при 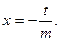
Оценим снизу:
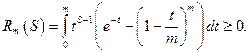
Оценка сверху:
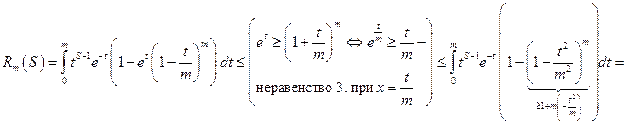
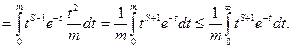
Итак,
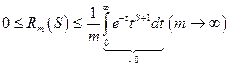 и по теореме «о двух милиционерах»
и по теореме «о двух милиционерах» 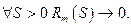
Доказано.
Лемма 1. 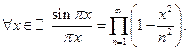
(подробно это доказывается в курсе теории функций комплексного переменного)
Формула дополнения для гамма-функции
Лемма 2. 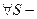 нецелого справедливо следующая формула дополнения
нецелого справедливо следующая формула дополнения 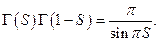
В частности, при 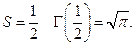
Доказательство. Имеем по формуле Эйлера
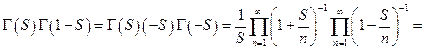
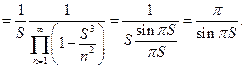
Доказано.
Задача. Вычислить 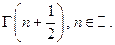
При 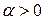 и
и 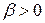 бета-функция Эйлера
бета-функция Эйлера 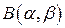 задается равенством:
задается равенством:
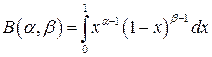 .
.
Подынтегральная функция имеет, вообще говоря, две особенности: при 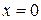 и при
и при 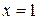 , поэтому представим интеграл в виде:
, поэтому представим интеграл в виде:
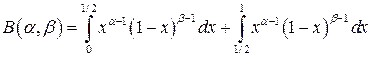 .
.
Сравнивая первый интеграл в правой части с интегралом 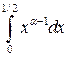 , а второй – с
, а второй – с 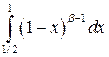 , которые сходятся соответственно при
, которые сходятся соответственно при 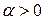 и
и 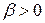 и соответственно расходятся при выполнении неравенств
и соответственно расходятся при выполнении неравенств 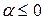 и
и 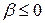 , получаем, что областью определения бета-функции в плоскости
, получаем, что областью определения бета-функции в плоскости 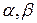 является прямой угол
является прямой угол 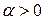 ,
, 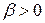 .
.
Из свойств бета-функции 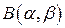 укажем следующие:
укажем следующие:
1) Для любых 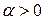 и
и 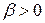 :
: 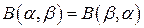 .
.
2) Для любых 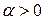 и
и 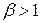 :
:
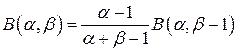 .
.
3) Для любых 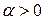
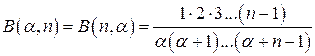 ,
, 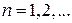
Теорема. Для 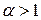 и
и 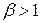 справедлива формула
справедлива формула
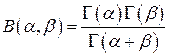 . (1)
. (1)
Замечание. Поскольку гамма - функция 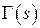 определена при всех
определена при всех 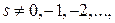 то формула (1) в теореме 6 позволяет распространить определение функции
то формула (1) в теореме 6 позволяет распространить определение функции 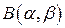 на все множество вещественных значений
на все множество вещественных значений 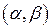 , за исключением точек
, за исключением точек 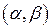 , где либо величина
, где либо величина 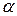 , либо величина
, либо величина 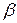 равна
равна 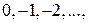 .
.
2. Формула Стирлинга
Изучение эйлеровских интегралов завершаем важной для приложений формулой Стирлинга, дающей приближенное значение для гамма-функции или для функции 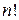 при больших значениях аргумента.
при больших значениях аргумента.
Теорема (формула Стирлинга). При 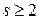 имеет место равенство:
имеет место равенство:
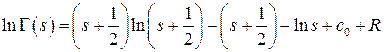 ,
,
где  , а для величины остатка R выполняются неравенства
, а для величины остатка R выполняются неравенства
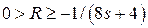 .
.
Отметим, что если воспользоваться соотношением
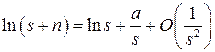 ,
,
то из теоремы 1 можно получить еще один вариант формулы Стирлинга вида:
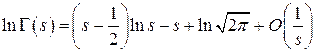 .
.
В частности, при 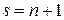 отсюда имеем
отсюда имеем
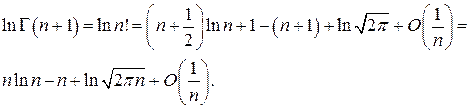
Следовательно, справедлива асимптотическая формула
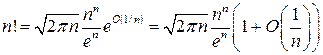 ,
,
которая также называется формулой Стирлинга. Более тщательные вычисления позволяют получить оценку вида 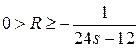 для остатка R в асимптотической формуле теоремы. Этот результат был установлен Гауссом. Он же доказал, что величину
для остатка R в асимптотической формуле теоремы. Этот результат был установлен Гауссом. Он же доказал, что величину 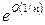 в асимптотической формуле для
в асимптотической формуле для 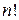 можно заменить на
можно заменить на 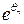 , где
, где 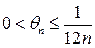 .
.
ЛЕКЦИЯ 12
Евклидово пространство интегрируемых функций. Ортонормированная система. Задача о наилучшем приближении элемента евклидова пространства по ортонормированной системе. Базисность и замкнутость ортонормированной системы. Ряд и коэффициенты Фурье. Неравенство Бесселя и равенство Парсеваля
1. Евклидово пространство интегрируемых функций
Пусть 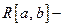 линейное пространство интегрируемых по Риману на отрезке [ a, b ] функций. В нём можно определить скалярное произведение:
линейное пространство интегрируемых по Риману на отрезке [ a, b ] функций. В нём можно определить скалярное произведение: 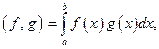 удовлетворяющее следующим аксиомам скалярного произведения:
удовлетворяющее следующим аксиомам скалярного произведения:
1) 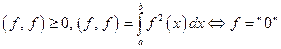 (нулевая функция – функция, принимающая нулевые значения в точках непрерывности и возможно положительные значения в точках разрыва, мера которых равна нулю, т.е. нулевая функция – это не одна, а целый класс функций).
(нулевая функция – функция, принимающая нулевые значения в точках непрерывности и возможно положительные значения в точках разрыва, мера которых равна нулю, т.е. нулевая функция – это не одна, а целый класс функций).
2) 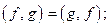
3) 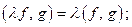
4) 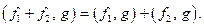
Линейное пространство со скалярным произведением называется Евклидовым пространством. Евклидово пространство можно рассматривать как нормированное, в котором норма определяется по правилам: 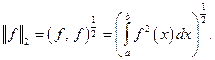 Для такого отображения выполнены все аксиомы нормы:
Для такого отображения выполнены все аксиомы нормы:
1) 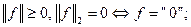
2) 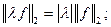
3) 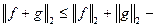 неравенство треугольника, и оно легко выводится из неравенства Коши-Буняковского
неравенство треугольника, и оно легко выводится из неравенства Коши-Буняковского 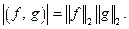
В свою очередь неравенство Коши-Буняковского позволяет определить и угол между функциями: 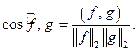 В частности,
В частности, 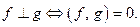 Норма позволяет определить расстояние между функциями и сходимость последовательности функций:
Норма позволяет определить расстояние между функциями и сходимость последовательности функций: 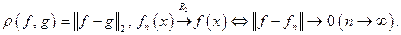 Такую сходимость называют среднеквадратичной сходимостью
Такую сходимость называют среднеквадратичной сходимостью 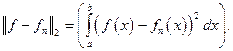
Сравним равномерную сходимость и среднеквадратичную сходимости на отрезке [ a, b ]. Из равномерной сходимости вытекает среднеквадратичная сходимость:
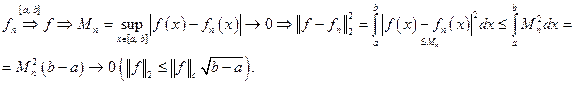
Обратное неверно.
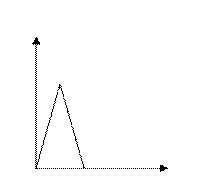
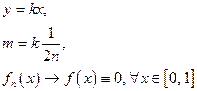
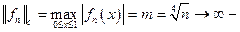 равномерной сходимости нет.
равномерной сходимости нет.
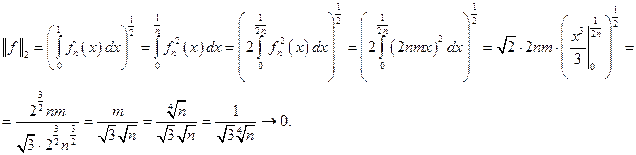
Пространство 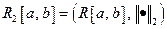 является бесконечномерным. В нём линейно-независимую систему, например, образуют функции
является бесконечномерным. В нём линейно-независимую систему, например, образуют функции 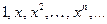 (система степеней).
(система степеней).
Задача. Охарактеризовать мощность пространства 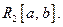
2. Ортонормированная система. Задача о наилучшем приближении элемента евклидова пространства по ортонормированной системе
Счётная система функций 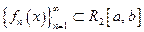 называется ортогональной, если
называется ортогональной, если 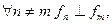 и ортонормированной, если система ортогональная и нормированная, т.е.
и ортонормированной, если система ортогональная и нормированная, т.е. 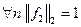 . Далее будем обозначать ОС – ортогональная система, ОНС – ортонормированная система.
. Далее будем обозначать ОС – ортогональная система, ОНС – ортонормированная система.
Рассмотрим задачу о наилучшем среднеквадратичном приближении функции по ОНС.
Пусть 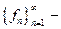 ОНС. Линейные комбинации вида
ОНС. Линейные комбинации вида 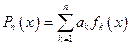 будем называть полиномами порядка n по этой ОНС. Множество всех таких полиномов порядка n будет образовывать линейное подпространство
будем называть полиномами порядка n по этой ОНС. Множество всех таких полиномов порядка n будет образовывать линейное подпространство 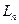 размерности п, т.е.
размерности п, т.е. 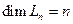 , с базисом
, с базисом 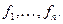
Задача. Доказать, что ОНС – линейно-независимая система.
Для 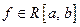 величина
величина 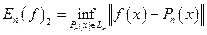 называется величиной наилучшего среднеквадратичного приближения функции f полиномами порядка п по нашей ОНС. Полином
называется величиной наилучшего среднеквадратичного приближения функции f полиномами порядка п по нашей ОНС. Полином 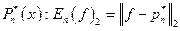 называется полиномом наилучшего среднеквадратичного приближения
называется полиномом наилучшего среднеквадратичного приближения
Теорема. 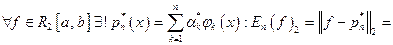
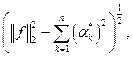 причём
причём 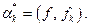
Доказательство. 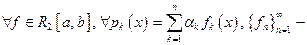 ОНС,
ОНС, 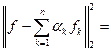
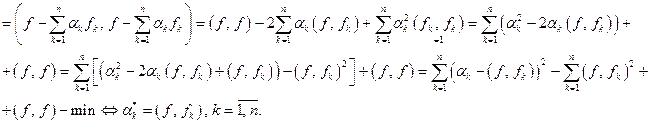 Итак,
Итак, 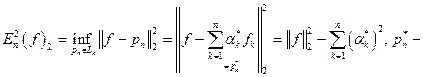 единственен.
единственен.
Доказано.
3. Ряд и коэффициенты Фурье. Неравенство Бесселя и равенство Парсеваля. Базисность и замкнутость ортонормированной системы
Если 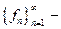 ОНС,
ОНС, 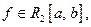 то функциональный ряд
то функциональный ряд 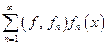 называется рядом Фурье функции f по ортонормированной системе
называется рядом Фурье функции f по ортонормированной системе 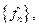 а коэффициенты этого ряда называются коэффициентами Фурье.
а коэффициенты этого ряда называются коэффициентами Фурье.
Частичные суммы ряда Фурье обладают экстремальным свойством: они являются полиномамими наилучшего среднеквадратичного приближения:
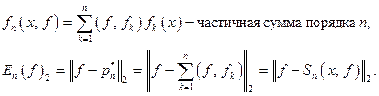
Итак, каждой функции из  можно поставить в соответствие её ряд Фурье. Какое отношение этот ряд Фурье имеет к функции?
можно поставить в соответствие её ряд Фурье. Какое отношение этот ряд Фурье имеет к функции?
Когда этот ряд в среднеквадратичном сходится к функции: 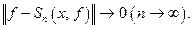 Ответы на эти вопросы зависят от свойств ОНС.
Ответы на эти вопросы зависят от свойств ОНС.
Имеем: 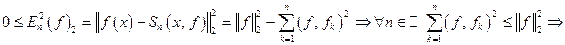
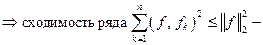 неравенство Бесселя.
неравенство Бесселя.
ОНС 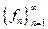 называется базисом в
называется базисом в  если
если 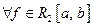 её ряд Фурье в среднеквадратичном сходится к ней, т.е. можно записать равенство
её ряд Фурье в среднеквадратичном сходится к ней, т.е. можно записать равенство 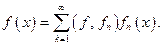
ОНС 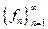 называется замкнутой в
называется замкнутой в 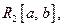 если множество всех полиномов по система плотно в
если множество всех полиномов по система плотно в 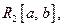 относительно среднеквадратичной сходимости, т.е.:
относительно среднеквадратичной сходимости, т.е.:
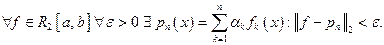
ОНС 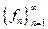 называется полной в
называется полной в 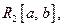 если не существует в
если не существует в 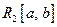 ненулевой функции, ортогональной всем функциям системы.
ненулевой функции, ортогональной всем функциям системы.
ОНС 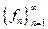 удовлетворяет равенству Парсеваля, если
удовлетворяет равенству Парсеваля, если 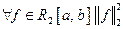 равна сумме квадратов коэффициентов Фурье, т.е.
равна сумме квадратов коэффициентов Фурье, т.е. 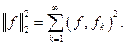
Теорема. Все четыре услови


 . Его полнота. 9
. Его полнота. 9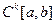 . Его полнота. 13
. Его полнота. 13 ................................................... 18
................................................... 18 сходится и определяет новую функцию. Это есть пример функционального ряда.
сходится и определяет новую функцию. Это есть пример функционального ряда.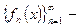 последовательность функций, определённых на одном и том же множестве
последовательность функций, определённых на одном и том же множестве 
 .
. предельная функция. Аналогично для функционального ряда
предельная функция. Аналогично для функционального ряда  область сходимости (поточечной сходимости) функционального ряда, а
область сходимости (поточечной сходимости) функционального ряда, а  сумма функционального ряда.
сумма функционального ряда. . Когда
. Когда  .
. Примеры. Пусть
Примеры. Пусть  .
.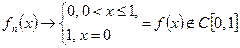 .
. Пример.
Пример.  .
.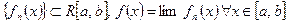 (R – интегрируема). Когда можно гарантировать, что
(R – интегрируема). Когда можно гарантировать, что  или
или  .
.

 .
. (С1- непрерывно дифференцируема). Когда
(С1- непрерывно дифференцируема). Когда  , или
, или  .
.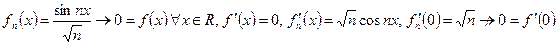 .
. на
на  .
. равномерно сходится на
равномерно сходится на  к f(x), т.е.
к f(x), т.е.  , если
, если 
 .
. , тогда эквивалентное определение равномерной сходимости выглядит так:
, тогда эквивалентное определение равномерной сходимости выглядит так:  .
. называется равномерно сходящимся к своей сумма на [ a, b ], если его последовательность частичных сумм сходится равномерно на [ a, b ] к S(x), т.е.
называется равномерно сходящимся к своей сумма на [ a, b ], если его последовательность частичных сумм сходится равномерно на [ a, b ] к S(x), т.е. 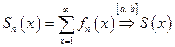 или
или

 , т.е. поточечная сходимость есть, а равномерной сходимости нет.
, т.е. поточечная сходимость есть, а равномерной сходимости нет.


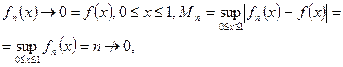

 т.е. равномерная сходимость есть, но и в этом случае её недостаточно.
т.е. равномерная сходимость есть, но и в этом случае её недостаточно. , или
, или  .
. , тогда
, тогда
 равномерная фундаментальность последовательности fn(x).
равномерная фундаментальность последовательности fn(x). (по критерию Коши)
(по критерию Коши)  . Запишем подробно условие равномерной фундаментальности:
. Запишем подробно условие равномерной фундаментальности: 
 .
. .
.
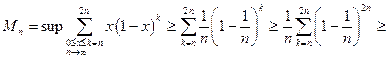
 равномерной сходимости нет.
равномерной сходимости нет.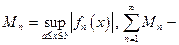 сходится, то
сходится, то 




 по признаку Вейерштрасса функциональный ряд сходится равномерно для всех
по признаку Вейерштрасса функциональный ряд сходится равномерно для всех  , хотя поточечно он сходится при
, хотя поточечно он сходится при  .
. можно показать, что для ряда
можно показать, что для ряда  справедливо следующее важное утверждение: частичные суммы ряда
справедливо следующее важное утверждение: частичные суммы ряда 


 воспользуемся преобразованием Абеля:
воспользуемся преобразованием Абеля:


 (1).
(1).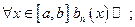




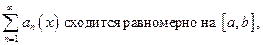 то ряд (1) сходится равномерно на
то ряд (1) сходится равномерно на 
 (невозрастающая)
(невозрастающая) 

 Если эти условия выполнены, то ряд сходится равномерно. Можно показать, что эти условия являются и необходимыми.
Если эти условия выполнены, то ряд сходится равномерно. Можно показать, что эти условия являются и необходимыми.


 Зафиксируем
Зафиксируем  функция
функция 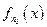 Î
Î равномерно непрерывна на [ a, b ]
равномерно непрерывна на [ a, b ] 

 непрерывна, функциональный ряд
непрерывна, функциональный ряд  то
то 
 частичные суммы, то
частичные суммы, то  также непрерывны и равномерно сходятся к
также непрерывны и равномерно сходятся к 

 - линейное пространство бесконечной размерности, в котором можно ввести норму
- линейное пространство бесконечной размерности, в котором можно ввести норму  для которой выполнены свойства:
для которой выполнены свойства:



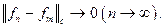 Нормированное пространство, в котором всякая фундаментальная последовательность является сходящейся, называется полным, или банаховым пространством (по имени С. Банаха).
Нормированное пространство, в котором всякая фундаментальная последовательность является сходящейся, называется полным, или банаховым пространством (по имени С. Банаха).




 также равномерно сходится к
также равномерно сходится к 
 .
. произвольное, а
произвольное, а 






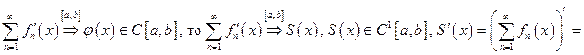

 то
то
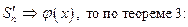

 - это множество
- это множество  раз непрерывно дифференцируемых на отрезке
раз непрерывно дифференцируемых на отрезке 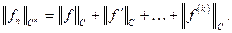

 эквивалентна равномерной сходимости самой последовательности и последовательности её производных до порядка k включительно.
эквивалентна равномерной сходимости самой последовательности и последовательности её производных до порядка k включительно. также является полным.
также является полным.
 непрерывна и имеет производные любого порядка и при
непрерывна и имеет производные любого порядка и при 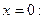
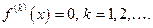




 называется рядом Тейлора в окрестности точки а.
называется рядом Тейлора в окрестности точки а.


 противоречие с возможностью разложения некоторой функции в некоторой окрестности. Т.е. одной бесконечной дифференцируемости функции недостаточно для разложения в ряд.
противоречие с возможностью разложения некоторой функции в некоторой окрестности. Т.е. одной бесконечной дифференцируемости функции недостаточно для разложения в ряд.
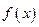 раскладывается в степенной ряд в точке а тогда и только тогда, когда:
раскладывается в степенной ряд в точке а тогда и только тогда, когда: Таким образом, вопрос о разложимости связан с ростом производных функции f. Укажем достаточные условия на рост производных для разложимости функций в степенной ряд.
Таким образом, вопрос о разложимости связан с ростом производных функции f. Укажем достаточные условия на рост производных для разложимости функций в степенной ряд. то
то 
 .
.
 Удобнее всего для этого рассмотреть ряд
Удобнее всего для этого рассмотреть ряд  и доказать его сходимость По признаку Даламбера получаем:
и доказать его сходимость По признаку Даламбера получаем: ряд сходится, и в таком случае предел общего члена равен нулю.
ряд сходится, и в таком случае предел общего члена равен нулю.


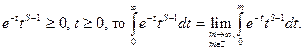
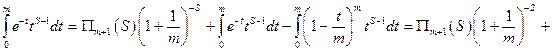
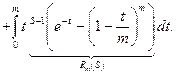
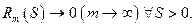
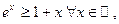
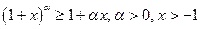 (неравенство Бернулли).
(неравенство Бернулли).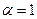 равенство очевидно.
равенство очевидно. верно.
верно.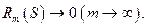
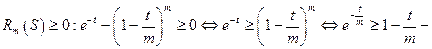 неравенство из 3. при
неравенство из 3. при 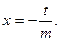
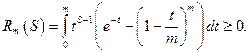
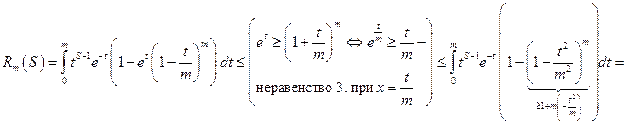
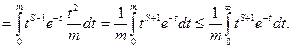
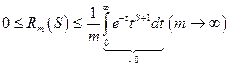 и по теореме «о двух милиционерах»
и по теореме «о двух милиционерах» 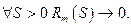
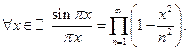
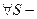 нецелого справедливо следующая формула дополнения
нецелого справедливо следующая формула дополнения 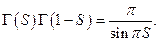
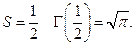
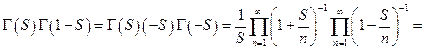
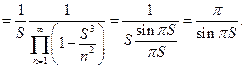
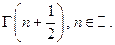
 и
и  бета-функция Эйлера
бета-функция Эйлера 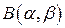 задается равенством:
задается равенством: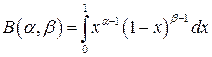 .
. и при
и при  , поэтому представим интеграл в виде:
, поэтому представим интеграл в виде: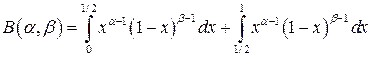 .
.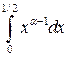 , а второй – с
, а второй – с 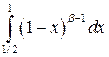 , которые сходятся соответственно при
, которые сходятся соответственно при 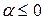 и
и 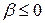 , получаем, что областью определения бета-функции в плоскости
, получаем, что областью определения бета-функции в плоскости 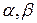 является прямой угол
является прямой угол 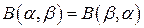 .
.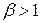 :
: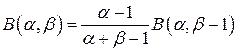 .
.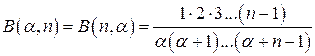 ,
, 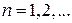
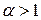 и
и 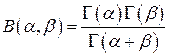 . (1)
. (1)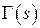 определена при всех
определена при всех 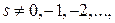 то формула (1) в теореме 6 позволяет распространить определение функции
то формула (1) в теореме 6 позволяет распространить определение функции 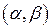 , за исключением точек
, за исключением точек 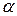 , либо величина
, либо величина 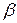 равна
равна 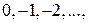 .
.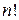 при больших значениях аргумента.
при больших значениях аргумента.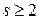 имеет место равенство:
имеет место равенство: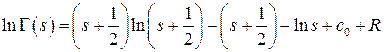 ,
, , а для величины остатка R выполняются неравенства
, а для величины остатка R выполняются неравенства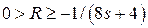 .
.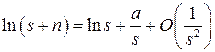 ,
,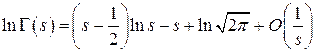 .
.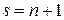 отсюда имеем
отсюда имеем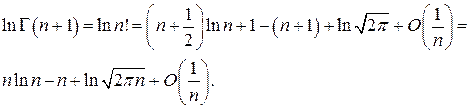
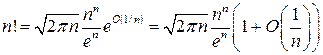 ,
,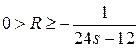 для остатка R в асимптотической формуле теоремы. Этот результат был установлен Гауссом. Он же доказал, что величину
для остатка R в асимптотической формуле теоремы. Этот результат был установлен Гауссом. Он же доказал, что величину 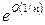 в асимптотической формуле для
в асимптотической формуле для 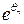 , где
, где 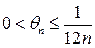 .
.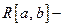 линейное пространство интегрируемых по Риману на отрезке [ a, b ] функций. В нём можно определить скалярное произведение:
линейное пространство интегрируемых по Риману на отрезке [ a, b ] функций. В нём можно определить скалярное произведение: 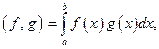 удовлетворяющее следующим аксиомам скалярного произведения:
удовлетворяющее следующим аксиомам скалярного произведения: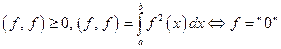 (нулевая функция – функция, принимающая нулевые значения в точках непрерывности и возможно положительные значения в точках разрыва, мера которых равна нулю, т.е. нулевая функция – это не одна, а целый класс функций).
(нулевая функция – функция, принимающая нулевые значения в точках непрерывности и возможно положительные значения в точках разрыва, мера которых равна нулю, т.е. нулевая функция – это не одна, а целый класс функций).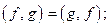
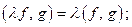
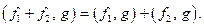
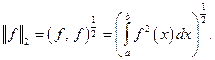 Для такого отображения выполнены все аксиомы нормы:
Для такого отображения выполнены все аксиомы нормы: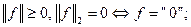
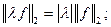
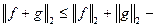 неравенство треугольника, и оно легко выводится из неравенства Коши-Буняковского
неравенство треугольника, и оно легко выводится из неравенства Коши-Буняковского 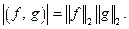
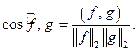 В частности,
В частности, 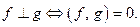 Норма позволяет определить расстояние между функциями и сходимость последовательности функций:
Норма позволяет определить расстояние между функциями и сходимость последовательности функций: 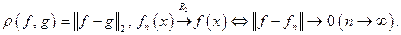 Такую сходимость называют среднеквадратичной сходимостью
Такую сходимость называют среднеквадратичной сходимостью 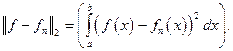
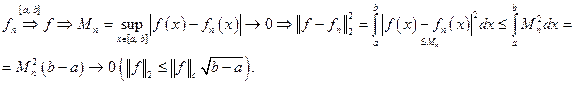

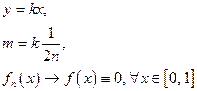
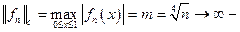 равномерной сходимости нет.
равномерной сходимости нет.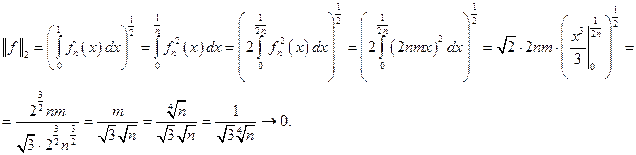
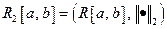 является бесконечномерным. В нём линейно-независимую систему, например, образуют функции
является бесконечномерным. В нём линейно-независимую систему, например, образуют функции 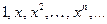 (система степеней).
(система степеней).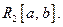
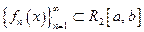 называется ортогональной, если
называется ортогональной, если 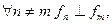 и ортонормированной, если система ортогональная и нормированная, т.е.
и ортонормированной, если система ортогональная и нормированная, т.е. 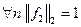 . Далее будем обозначать ОС – ортогональная система, ОНС – ортонормированная система.
. Далее будем обозначать ОС – ортогональная система, ОНС – ортонормированная система.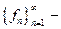 ОНС. Линейные комбинации вида
ОНС. Линейные комбинации вида 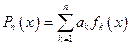 будем называть полиномами порядка n по этой ОНС. Множество всех таких полиномов порядка n будет образовывать линейное подпространство
будем называть полиномами порядка n по этой ОНС. Множество всех таких полиномов порядка n будет образовывать линейное подпространство 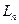 размерности п, т.е.
размерности п, т.е. 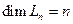 , с базисом
, с базисом 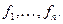
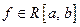 величина
величина 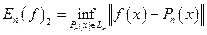 называется величиной наилучшего среднеквадратичного приближения функции f полиномами порядка п по нашей ОНС. Полином
называется величиной наилучшего среднеквадратичного приближения функции f полиномами порядка п по нашей ОНС. Полином 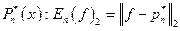 называется полиномом наилучшего среднеквадратичного приближения
называется полиномом наилучшего среднеквадратичного приближения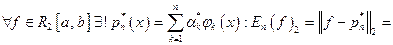
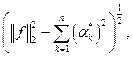 причём
причём 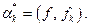
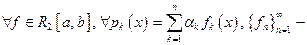 ОНС,
ОНС, 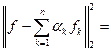
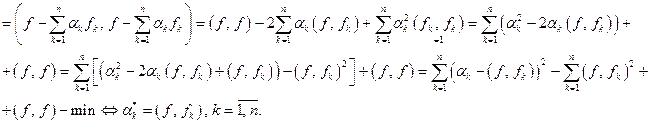 Итак,
Итак, 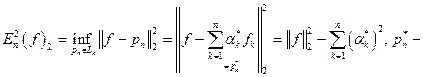 единственен.
единственен.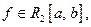 то функциональный ряд
то функциональный ряд 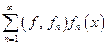 называется рядом Фурье функции f по ортонормированной системе
называется рядом Фурье функции f по ортонормированной системе 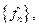 а коэффициенты этого ряда называются коэффициентами Фурье.
а коэффициенты этого ряда называются коэффициентами Фурье.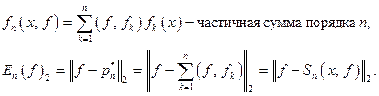
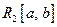 можно поставить в соответствие её ряд Фурье. Какое отношение этот ряд Фурье имеет к функции?
можно поставить в соответствие её ряд Фурье. Какое отношение этот ряд Фурье имеет к функции?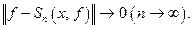 Ответы на эти вопросы зависят от свойств ОНС.
Ответы на эти вопросы зависят от свойств ОНС.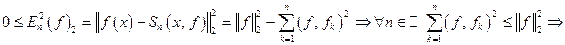
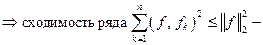 неравенство Бесселя.
неравенство Бесселя.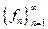 называется базисом в
называется базисом в 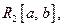 если
если 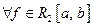 её ряд Фурье в среднеквадратичном сходится к ней, т.е. можно записать равенство
её ряд Фурье в среднеквадратичном сходится к ней, т.е. можно записать равенство 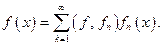
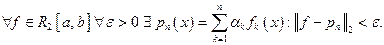
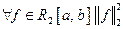 равна сумме квадратов коэффициентов Фурье, т.е.
равна сумме квадратов коэффициентов Фурье, т.е.