1. Сходимость и сумма числового ряда. Необходимые условия сходимости
Пусть  последовательность действительных чисел,
последовательность действительных чисел,
 - числовой ряд. (1)
- числовой ряд. (1)
Составим последовательность частичных сумм:

 последовательность частичных сумм.
последовательность частичных сумм.
Если для ряда (1) существует предел последовательность частичных сумм при  , равный числу
, равный числу  , то ряд называется сходящимся, а число S – его суммой. В противном случае ряд (1) называется расходящимся.
, то ряд называется сходящимся, а число S – его суммой. В противном случае ряд (1) называется расходящимся.
Пример. Исследовать сходимость и найти сумму ряда  .
.
Составляем последовательность частичных сумм:
 ,
,
 .
.
 остаток сходящегося ряда,
остаток сходящегося ряда,  последовательность остатков.
последовательность остатков.
Первое необходимое условие сходимости. Частичные суммы сходящегося ряда – ограничены:  (это вытекает из того, что сходящаяся последовательность ограничена).
(это вытекает из того, что сходящаяся последовательность ограничена).
Приведём пример ряда, у которого частичные суммы ограничены, а сам ряд будет расходиться:

Второе необходимое условие сходимости У сходящегося ряда предел общего члена равен нулю 
Доказательство.  Доказано.
Доказано.
Рассмотрим пример расходящегося ряда, для которого 

неограниченная, наименьшее слагаемое  .
.
Пример.  расходится, т.к.
расходится, т.к. 
Предположим, что 
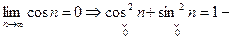 противоречие.
противоречие.
2. Свойства сходящихся числовых рядов. Критерий Коши
1. Критерий сходимости: ряд сходится 
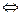

Доказательство.  Доказано.
Доказано.
2. Сходимость ряда не нарушится, если добавить или отбросить конечное число слагаемых.
3. Множество сходящихся радов образуют линейное пространство:
если 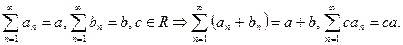
4. Критерий Коши: ряд (1) сходится  фундаментальная, т.е.
фундаментальная, т.е. 
Пример.  гармонический ряд (расходящийся).
гармонический ряд (расходящийся).

 т.е. не выполнен критерий Коши, ряд расходится.
т.е. не выполнен критерий Коши, ряд расходится.


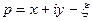 -функция Римана.
-функция Римана.
Задача. Исследовать сходимость ряда 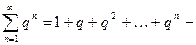 сумма бесконечной геометрической прогрессии. Доказать, что при
сумма бесконечной геометрической прогрессии. Доказать, что при  ряд сходится,
ряд сходится, 
Решение.


ЛЕКЦИЯ 14
Сходимость рядов с положительными членами. Критерий сходимости. Признаки сравнения. Признак Даламбера
1. Сходимость рядов с положительными членами. Критерий сходимости
Пусть
 положительный ряд (1).
положительный ряд (1).
Теорема. Ряд (1) – сходится тогда и только тогда, когда последовательность  ограниченная.
ограниченная.
Доказательство. Необходимость.
Известно как необходимое условие сходимости.
Достаточность.
 ограниченная
ограниченная  т.е.
т.е.  сходится (по теореме Коши о пределе монотонной последовательности). Доказано.
сходится (по теореме Коши о пределе монотонной последовательности). Доказано.
Замечание. У положительного ряда достаточно проверять ограниченность только некоторой подпоследовательности частичных сумм.
2. Признаки сравнения
Теорема. Если даны два ряда  то:
то:
1) если 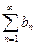 - сходится, то
- сходится, то  - сходится;
- сходится;
2) если  - расходится, то
- расходится, то 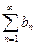 - расходится.
- расходится.
Доказательство.
1) Пусть  подпоследовательность частичных сумм ряда
подпоследовательность частичных сумм ряда 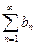 ,
,  подпоследовательность частичных сумм ряда
подпоследовательность частичных сумм ряда 
 ограниченная сверху (по необходимому условию сходимости),
ограниченная сверху (по необходимому условию сходимости),  ограниченная сверху
ограниченная сверху  сходится.
сходится.
Вторая часть теоремы доказывается аналогично.
Доказано.
Замечание. В признаке сравнения выполнение неравенства  достаточно требовать для
достаточно требовать для 
При использовании признака сравнения можно использовать сравнение последовательностей:
1. если  и ряд
и ряд  сходится, то ряд (1) сходится;
сходится, то ряд (1) сходится;
2. если  то сходимости
то сходимости  и
и  эквиваленты;
эквиваленты;
3. 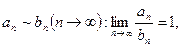 то сходимости
то сходимости  и
и  эквивалентны.
эквивалентны.
Пример. Исследовать на сходимость 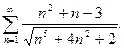 :
:
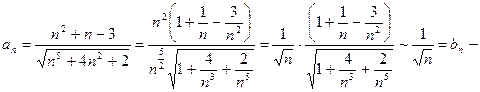 расходится, а значит и данный ряд
расходится, а значит и данный ряд  расходится.
расходится.
Признак сравнения в предельной форме
Если даны  то
то
1) если ряд  сходится,
сходится,  то ряд
то ряд  - сходится;
- сходится;
если ряд  расходится,
расходится,  то ряд
то ряд  - расходится.
- расходится.
Обобщенный признак сравнения
Теорема. Если даны  то
то
1) если 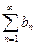 - сходится, то
- сходится, то  - сходится;
- сходится;
2) если  - расходится, то
- расходится, то 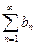 - расходится.
- расходится.
Доказательство.
1) Имеем  или
или  или
или  или
или
 Þ
Þ  - сходится.
- сходится.
Вторая часть теоремы доказывается аналогично.
Доказано.
Замечание. В обобщённом признаке сравнения выполнение неравенств  достаточно требовать для
достаточно требовать для 
3. Признак Даламбера
Если для ряда 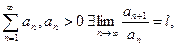 то
то 
Доказательство. Пусть 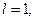 тогда ряд
тогда ряд  сходится,
сходится,  расходится, но
расходится, но 
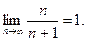
Пусть  тогда
тогда  и для
и для  сходится и по обобщённому признаку сравнения исходный ряд сходится.
сходится и по обобщённому признаку сравнения исходный ряд сходится.
Пусть 

Значит, ряд расходится.
Доказано.
Признак Даламбера с использованием нижнего и верхнего предела:
1) Если  то ряд сходится.
то ряд сходится.
2) Если  то ряд расходится и
то ряд расходится и 
ЛЕКЦИЯ 15



 последовательность действительных чисел,
последовательность действительных чисел, - числовой ряд. (1)
- числовой ряд. (1)
 последовательность частичных сумм.
последовательность частичных сумм. , равный числу
, равный числу  , то ряд называется сходящимся, а число S – его суммой. В противном случае ряд (1) называется расходящимся.
, то ряд называется сходящимся, а число S – его суммой. В противном случае ряд (1) называется расходящимся. .
. ,
, .
. остаток сходящегося ряда,
остаток сходящегося ряда,  последовательность остатков.
последовательность остатков. (это вытекает из того, что сходящаяся последовательность ограничена).
(это вытекает из того, что сходящаяся последовательность ограничена).

 Доказано.
Доказано.

 .
. расходится, т.к.
расходится, т.к. 

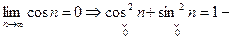 противоречие.
противоречие.
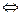

 Доказано.
Доказано.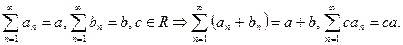
 фундаментальная, т.е.
фундаментальная, т.е. 
 гармонический ряд (расходящийся).
гармонический ряд (расходящийся).
 т.е. не выполнен критерий Коши, ряд расходится.
т.е. не выполнен критерий Коши, ряд расходится.

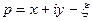 -функция Римана.
-функция Римана.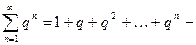 сумма бесконечной геометрической прогрессии. Доказать, что при
сумма бесконечной геометрической прогрессии. Доказать, что при  ряд сходится,
ряд сходится, 


 положительный ряд (1).
положительный ряд (1). ограниченная.
ограниченная. т.е.
т.е.  сходится (по теореме Коши о пределе монотонной последовательности). Доказано.
сходится (по теореме Коши о пределе монотонной последовательности). Доказано. то:
то: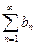 - сходится, то
- сходится, то  - сходится;
- сходится; подпоследовательность частичных сумм ряда
подпоследовательность частичных сумм ряда  ограниченная сверху (по необходимому условию сходимости),
ограниченная сверху (по необходимому условию сходимости),  ограниченная сверху
ограниченная сверху  сходится.
сходится. достаточно требовать для
достаточно требовать для 
 и ряд
и ряд  сходится, то ряд (1) сходится;
сходится, то ряд (1) сходится; то сходимости
то сходимости 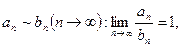 то сходимости
то сходимости 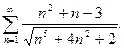 :
: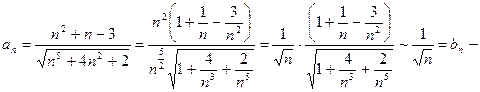 расходится, а значит и данный ряд
расходится, а значит и данный ряд  расходится.
расходится. то
то то ряд
то ряд  то ряд
то ряд  то
то или
или  или
или  или
или Þ
Þ  достаточно требовать для
достаточно требовать для 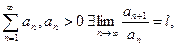 то
то 
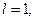 тогда ряд
тогда ряд  сходится,
сходится, 
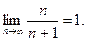
 тогда
тогда  и для
и для  сходится и по обобщённому признаку сравнения исходный ряд сходится.
сходится и по обобщённому признаку сравнения исходный ряд сходится.

 то ряд сходится.
то ряд сходится. то ряд расходится и
то ряд расходится и 



